Chapter 5: Digital Building Blocks

第五章主要探讨数字设计的基本构建模块。在现代计算设备的设计与实现过程中，数字构建模块承担着基础性的角色。本章将深入介绍这些核心组件，并为后续章节打下坚实的理论与实践基础。

Chapter 5 :: Topics

本章的主要内容包括：

• Introduction：概述数字构建模块的基本概念及其在计算机架构中的作用。
• Arithmetic Circuits：探讨用于数字计算的算术电路，例如加法器、乘法器等。
• Number Systems：介绍不同的数字系统，尤其是二进制和十六进制等在数字设计中的应用。
• Sequential Building Blocks：讨论时序电路，如触发器和计数器，它们依赖于时钟信号的顺序性。
• Memory Arrays：介绍存储器阵列，尤其是静态和动态存储器的实现。
• Logic Arrays：讲解逻辑阵列，它们是组合电路的重要组成部分，广泛应用于复杂的数字设计中。

这部分的图示展示了计算机系统的层次结构，从物理层、设备层到应用软件层，而本章则重点讨论逻辑和数字电路层次中的关键模块，这些模块为微架构和架构设计提供了基础。

Introduction

数字构建模块的基本概念

数字构建模块包括各种基础组件，诸如门电路、多路复用器、解码器、寄存器、算术电路、计数器、存储器阵列以及逻辑阵列。这些构建模块通过多种方式相互组合，形成复杂的计算设备的基本单元。这种设计思路体现了数字电路的层次性（Hierarchy）、模块化（Modularity）和规则性（Regularity）。具体来说：

• 层次性：复杂系统可以通过由简单组件组成的层次结构来构建。这使得设计可以逐步扩展，系统变得更易于理解和维护。
• 模块化：各个组件作为独立的模块存在，它们有明确的接口和功能定义。这种模块化设计的优势在于可以将功能单元重新组合、替换或升级，而不影响整个系统的其他部分。
• 规则性：由于构建模块的结构具有一致性和可扩展性，系统设计可以随着需求的增长而轻松扩展。这种规则性使得设计过程更加高效，并有助于实现规模化制造。

构建模块的实际应用

数字构建模块在现代微处理器的设计中发挥了重要作用。通过这些模块，设计者能够以简洁而高效的方式实现复杂的数字运算与控制逻辑。在第七章中，将会结合这些基础知识，构建出一个完整的微处理器。这不仅进一步深化对数字电路的理解，还能够展示如何从基础模块逐步扩展到复杂的计算设备。

Adders

加法器是数字电路设计中的基本组件之一，它们的主要功能是执行二进制数的加法运算。加法器不仅仅用于基本的加法运算，它们也是其他复杂运算电路如乘法器、除法器的基础。加法器的设计直接影响数字系统的速度和性能，因此理解其结构和工作原理对于数字电路设计至关重要。

1-Bit Adders

半加器 (Half Adder)

半加器是最简单的一位加法器，能够实现两个一位二进制数的加法。它有两个输入端：A和B，输出则分为两个部分，一个是和（Sum，S），另一个是进位（Carry out，Cout）。对于半加器而言，它只处理两位数的加法，并没有考虑进位输入。它的工作原理通过逻辑运算实现：

• A 和 B 的值分别为 0 或 1。
• 结果 S 是 A 和 B 的异或 (XOR) 运算结果。
• 进位 Cout 则是 A 和 B 的与 (AND) 运算结果。

下方的真值表展示了半加器的运算逻辑：

A	B	Cout	S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

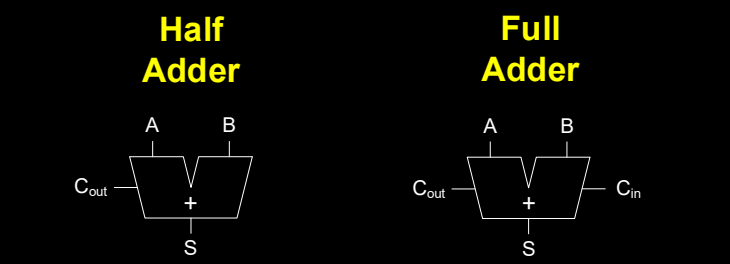
全加器 (Full Adder)

全加器则是更为复杂的加法器，它不仅能够处理 A 和 B 两个输入，还能够处理前一位的进位输入 Cin。因此，全加器能够实现多位数的加法运算。它的工作原理如下：

• A、B 为两个输入位，Cin 为前一位传递过来的进位输入。
• 结果 S 是 A、B 和 Cin 的异或 (XOR) 运算结果。
• 进位 Cout 是由 A 和 B 的与 (AND) 运算，再加上 Cin 和 A、B 的部分逻辑组合运算得到的。

全加器的真值表如下：

Cin	A	B	Cout	S
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

全加器是通过组合多个半加器及额外的逻辑门实现的。全加器能够处理输入进位，这使得它可以级联构成多位加法器，用于更复杂的二进制数加法。

Multibit Adders: CPAs

对于多位二进制数的加法，单独使用一个全加器是不够的，因此需要多位加法器，也就是进位传播加法器（Carry Propagate Adders，CPAs）。这些加法器通过多个全加器的串联来实现。根据进位信号的传播方式，不同类型的进位传播加法器有不同的性能表现。

进位传播加法器的类型

• Ripple-carry Adder 波纹进位加法器：这是最简单的多位加法器，它依赖于每一位的进位信号顺序传递到下一位。虽然设计简单，但因为每个位的运算必须等待前一位的进位信号，速度较慢，适合小规模加法运算。

• Carry-lookahead Adder 超前进位加法器：为了解决进位传播的延迟问题，超前进位加法器通过逻辑电路提前计算每一位的进位信号，减少了运算的依赖顺序，从而大大提高了速度。它适用于较大规模的加法运算，但其硬件复杂度也相应增加。

• Prefix Adder 前缀加法器：这是比超前进位加法器更快的设计，它使用前缀结构进一步减少进位信号传播的时间。虽然速度更快，但实现所需的硬件资源也更多，适合对性能要求极高的应用场景。

硬件与性能的平衡

超前进位加法器和前缀加法器虽然能够显著加快运算速度，但相应的硬件复杂度也较高。这意味着它们需要更多的逻辑门和布线。因此，在实际应用中，设计者通常需要在性能和硬件资源之间进行权衡，以选择最适合具体应用需求的加法器类型。

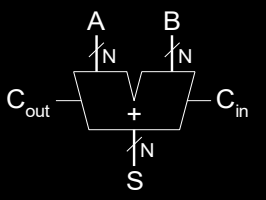
图中的符号展示了多位加法器的输入输出结构，输入包括多位的A和B以及Cin，输出为和（S）和进位（Cout）。

Ripple Carry Addition

在数字电路设计中，Ripple-Carry Adder（RCA，纹波进位加法器） 是最基础的多位二进制数加法器，它通过将多个一位的全加器串联起来实现多位数的加法。该结构的基本思想是将一个位的加法结果及其产生的进位传递到下一位的加法器中，以此类推直到完成所有位的加法运算。

Ripple-Carry Adder

纹波进位加法器由多个一位全加器组成，每个全加器负责处理两个输入位（A 和 B）和一个进位输入（Cin）。当一位的加法完成后，结果 S 和进位 Cout 产生，进位 Cout 会传递给下一个全加器作为其 Cin，从而完成进位的逐级传递。其工作机制如下：

• 链式连接：多个一位全加器通过进位连接，形成一个进位链。
• 进位传播：每一位的加法需要等待前一位的进位结果，因此进位会在加法器链中逐位传播。

这种设计虽然简单且容易实现，但其主要缺点是速度慢。进位信号需要依次从最低位传播到最高位，导致在大规模加法运算时，整个计算速度受到每一级进位传播延迟的制约。即使输入位数较多，计算仍需依赖于前面的进位结果，这种逐位传播的过程限制了加法器的性能。

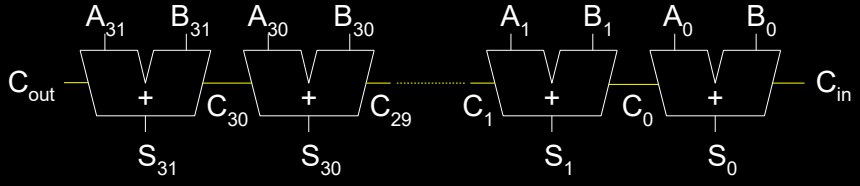
图中展示了一个 32 位的纹波进位加法器示例，从 A₀、B₀ 的最低位到 A₃₁、B₃₁ 的最高位，每个全加器之间通过进位信号 Cout 连接。

Ripple-Carry Adder Delay

在纹波进位加法器中，延迟 是影响其性能的关键因素。由于每个位的加法都需要等待前一位的进位结果传递，因此整个加法器的延迟是由所有全加器的延迟之和决定的。具体来说，纹波进位加法器的延迟公式可以表示为：

\[ t_{\text{ripple}} = N \times t_{\text{FA}} \]

其中：

• \( N \) 是加法器的位数（例如 32 位加法器，N = 32）。
• \( t_{\text{FA}} \) 是每个一位全加器的延迟。

这意味着，对于一个位数为 N 的加法器，延迟将与 N 成正比。随着位数的增加，延迟也会显著增加，因此 Ripple-Carry Adder 并不适合处理大规模的加法运算。

虽然纹波进位加法器的设计结构简单，但其性能限制使得它在大规模应用场景中效率较低。为了解决这个问题，设计者通常会考虑其他类型的加法器，如超前进位加法器或前缀加法器，它们通过减少进位传播的层次或优化进位信号的计算，显著降低了延迟，从而提高了运算速度。

Chapter 5: Digital Building Blocks - Carry Lookahead Addition

Carry-Lookahead Adder 超前进位加法器

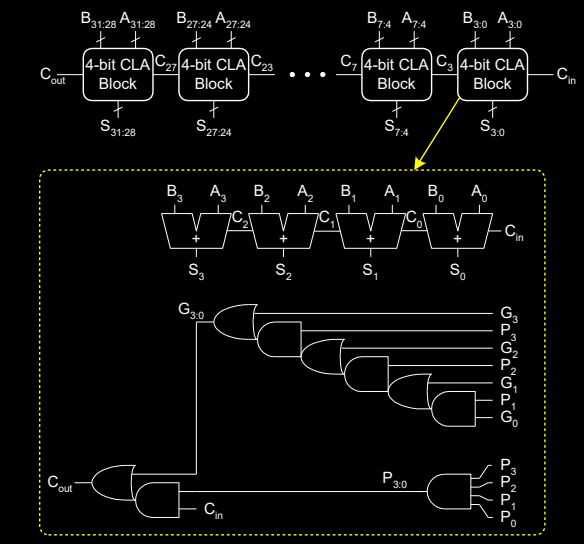
Carry-Lookahead Adder 旨在通过“生成”（generate）和“传播”（propagate）信号来计算 k 位块的进位输出（Cout）。它通过减少进位的逐级传递时间来加速加法运算，避免了传统进位链加法器中的延时问题。

超前进位加法器（Carry Look-Ahead Adder）是一种用于快速执行二进制加法的电路，旨在解决传统的串行进位加法器中进位传播导致的延迟问题。它通过提前计算进位信号，实现了加法运算的并行处理，从而大大提高了运算速度。

以下是超前进位加法器的计算过程：

1. 定义生成（Generate）和传播（Propagate）信号

对于每一位 \( i \)（从0开始编号），定义如下信号：

• 生成信号（\( G_i \)）：当这一位会生成一个进位时，\( G_i = 1 \)。

  \[ G_i = A_i \cdot B_i \]

• 传播信号（\( P_i \)）：当这一位会将进位传播到下一位时，\( P_i = 1 \)。

  \[ P_i = A_i \oplus B_i \]

其中：

• \( A_i \) 和 \( B_i \) 是被加数和加数的第 \( i \) 位。
• “\( \cdot \)” 表示逻辑与操作。
• “\( \oplus \)” 表示逻辑异或操作。

2. 计算进位信号

利用生成和传播信号，计算各个位的进位信号 \( C_i \)：

• 初始进位（\( C_0 \)）：通常为0或根据具体情况而定。

• 后续进位（\( C_{i+1} \)）：

  \[ C_{i+1} = G_i + (P_i \cdot C_i) \]

这是因为下一位的进位要么是当前位生成的进位，要么是当前位传播了前一位的进位。

展开计算进位信号（以4位加法器为例）：

• \( C_1 \)（第1位进位）：

  \[ C_1 = G_0 + (P_0 \cdot C_0) \]

• \( C_2 \)（第2位进位）：

  \[ C_2 = G_1 + (P_1 \cdot C_1) \]

  将 \( C_1 \) 展开：

  \[ C_2 = G_1 + (P_1 \cdot G_0) + (P_1 \cdot P_0 \cdot C_0) \]

• \( C_3 \)（第3位进位）：

  \[ C_3 = G_2 + (P_2 \cdot C_2) \]

  展开 \( C_2 \)：

  \[ C_3 = G_2 + (P_2 \cdot G_1) + (P_2 \cdot P_1 \cdot G_0) + (P_2 \cdot P_1 \cdot P_0 \cdot C_0) \]

• \( C_4 \)（第4位进位）：

  \[ C_4 = G_3 + (P_3 \cdot C_3) \]

  展开 \( C_3 \)：

  \[ C_4 = G_3 + (P_3 \cdot G_2) + (P_3 \cdot P_2 \cdot G_1) + (P_3 \cdot P_2 \cdot P_1 \cdot G_0) + (P_3 \cdot P_2 \cdot P_1 \cdot P_0 \cdot C_0) \]

3. 计算和位

有了进位信号后，计算每一位的和 \( S_i \)：

\[ S_i = P_i \oplus C_i \]

其中：

• \( P_i \) 是第 \( i \) 位的传播信号。
• \( C_i \) 是第 \( i \) 位的进位信号。

4. 计算示例

假设我们有两个4位二进制数 \( A \) 和 \( B \)：

• \( A = 1101 \)
• \( B = 1011 \)
• 初始进位 \( C_0 = 0 \)

步骤1：计算 \( G_i \) 和 \( P_i \)

位（\( i \)）	\( A_i \)	\( B_i \)	\( G_i = A_i \cdot B_i \)	\( P_i = A_i \oplus B_i \)
0	1	1	1	0
1	0	1	0	1
2	1	0	0	1
3	1	1	1	0

步骤2：计算进位 \( C_i \)

• \( C_1 = G_0 + (P_0 \cdot C_0) = 1 + (0 \cdot 0) = 1 \)
• \( C_2 = G_1 + (P_1 \cdot C_1) = 0 + (1 \cdot 1) = 1 \)
• \( C_3 = G_2 + (P_2 \cdot C_2) = 0 + (1 \cdot 1) = 1 \)
• \( C_4 = G_3 + (P_3 \cdot C_3) = 1 + (0 \cdot 1) = 1 \)

步骤3：计算和位 \( S_i \)

• \( S_0 = P_0 \oplus C_0 = 0 \oplus 0 = 0 \)
• \( S_1 = P_1 \oplus C_1 = 1 \oplus 1 = 0 \)
• \( S_2 = P_2 \oplus C_2 = 1 \oplus 1 = 0 \)
• \( S_3 = P_3 \oplus C_3 = 0 \oplus 1 = 1 \)

结果

• 和 \( S = S_3 S_2 S_1 S_0 = 1000 \)
• 最终进位 \( C_4 = 1 \)

因此，\( A + B = 1~1000 \)

超前进位加法器的主要优点是能够显著减少加法运算的延迟，因为它避免了逐位等待进位信号的传播。通过并行计算进位信号，运算速度与位数的关系不再是线性的，而是可以设计成对数级的，提高了电路的效率。

超前进位加法器通过引入生成和传播信号，提前计算进位，从而实现了快速的二进制加法。这种方法在现代高速计算中被广泛采用，尤其是在需要快速执行大量加法运算的场合，如CPU的算术逻辑单元（ALU）中。

Carry-Lookahead Adder Delay

在多位超前进位加法器中，计算延迟 \( t_{CLA} \) 是衡量其效率的一个关键指标。延迟由多个因素共同决定，具体公式如下：

\[ t_{CLA} = t_{pg} + t_{pg_block} + \left( \frac{N}{k} - 1 \right) t_{AND_OR} + k \cdot t_{FA} \]

• \( t_{pg} \): 计算每个位的生成信号 \( G_i \) 和传播信号 \( P_i \) 所需的时间。
• \( t_{pg_block} \): 计算每个块的生成信号 \( G_{j} \) 和传播信号 \( P_{j} \) 所需的时间（针对 k 位块）。
• \( t_{AND_OR} \): 从输入进位 \( C_{in} \) 到块的输出进位 \( C_{out} \) 的 AND/OR 门延迟。
• \( t_{FA} \): 每个全加器 (Full Adder) 的运算延迟。

对于 N 位 的超前进位加法器，尤其是当 N 大于 16 时，CLA 的运算速度比 Ripple-Carry Adder 快得多。这是因为 CLA 可以在生成和传播逻辑中同时计算多个块的进位，从而避免了逐位传播进位的瓶颈。

Prefix Addition

Prefix Adder：是 CLA 的扩展和优化。参见：MIT6.004 CLAs

Prefix Adder 的并行计算结构，使其能够在大规模加法运算中显著减少延迟。通过逐步计算生成和传播信号，Prefix Adder 可以在 \( \log_2 N \) 阶段内完成加法运算，大幅提升运算速度，尤其适用于高位宽的场景。

Prefix Adder Example

Prefix Adder 的计算步骤

Prefix Adder 的核心是逐步计算生成信号 \( G \) 和传播信号 \( P \)，并通过前缀的方式加速进位的传播。具体步骤如下：

• Step 1: 计算 1-bit block 的 \( P \) 和 \( G \) 信号。
  • 每一位的 \( P \) 和 \( G \) 信号分别根据 \( P_i = A_i + B_i \) 和 \( G_i = A_i \cdot B_i \) 来计算，表示这一位是否会生成进位或传播进位。
• Step 2: 计算 2-bit blocks 的 \( P \) 和 \( G \) 信号。
  • 对于 2 位块，将相邻的位组合，计算块的 \( P \) 和 \( G \)，即传播信号和生成信号的组合。
• Step 3: 计算 4-bit blocks 的 \( P \) 和 \( G \) 信号。
  • 再次扩展，计算 4 位块的生成和传播信号，逐步向更高的位数扩展。

• Step 4: 持续扩展到更大的块，如 8-bit、16-bit 块，直到覆盖整个加法器位宽。

• Step 5: 利用计算得到的前缀信号计算每一位的和 \( S_i \)： \[ S_i = (A_i \oplus B_i) \oplus C_{i-1} \] 其中，\( C_{i-1} \) 是通过前缀运算生成的进位。

通过这种递归扩展，Prefix Adder 能够并行计算出多位的生成和传播信号，从而快速确定进位并减少加法运算的延迟。

Prefix Adder Schematic

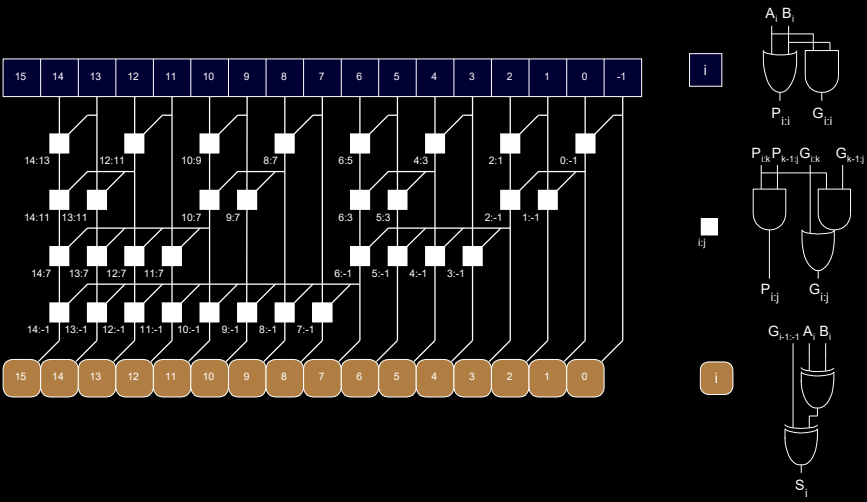
图示展示了 Prefix Adder 的逻辑结构。每一列代表一位的生成和传播信号的计算过程：

• 方块 表示特定位的 \( G \) 和 \( P \) 信号。
• 垂直和对角线箭头 代表进位的传播路径。每一位的进位根据前面几位的生成和传播信号递归计算出来。
• 最终，每一位的和 \( S_i \) 通过最后一层的异或门计算。

Schematic 说明

1. P 和 G 的计算：最左边的各位初始计算 \( P \) 和 \( G \) 信号。
2. 逐步合成前缀信号：各位的 \( G_{i:j} \) 和 \( P_{i:j} \) 信号通过多个阶段逐层合成，形成前缀树结构。每一层表示一组位块的计算范围逐渐扩大。
3. 和的计算：通过已经计算好的进位前缀，最终计算出每个位的和 \( S_i \)。

这种前缀树结构的设计使得进位的计算可以在 \( \log_2 N \) 的时间内完成，因此 Prefix Adder 是一种非常高效的多位加法器，特别适合处理高位宽的数据。

Prefix Adder Delay

Prefix Adder 的延迟主要由生成和传播信号的计算、前缀单元的合成以及最终的和运算组成。计算 Prefix Adder 延迟的公式如下：

\[ t_{PA} = t_{pg} + \log_2 N \cdot t_{pg_prefix} + t_{XOR} \]

• \( t_{pg} \): 计算每个位的生成信号 \( G_i \) 和传播信号 \( P_i \) 所需的延迟，通常由 AND 或 OR 门的延迟决定。
• \( t_{pg_prefix} \): 前缀单元的延迟，主要由方块中的前缀单元（AND-OR 门）的延迟决定。前缀单元通过组合多个位的 \( P_i \) 和 \( G_i \) 信号来快速生成进位。
• \( t_{XOR} \): 最后计算和 \( S_i \) 的异或门延迟。

因为 Prefix Adder 采用了并行化的前缀结构，延迟随着输入位数 N 的对数 \( \log_2 N \) 增长，使其相较于其他类型的加法器在大位宽的场景下更高效。

Adder Delay Comparisons

这部分比较了 32 位 Ripple-Carry Adder (RCA)、Carry-Lookahead Adder (CLA) 和 Prefix Adder 的延迟，特别是当 CLA 使用了 4 位块时的性能。

• Ripple-Carry Adder 延迟 \( t_{ripple} \): 因为进位信号需要逐位传播，RCA 的延迟与位数成正比。对于 32 位加法器，Ripple-Carry Adder 的延迟很大，尤其当位数增加时，性能显著下降。

• Carry-Lookahead Adder 延迟 \( t_{CLA} \): CLA 的延迟由生成和传播信号的计算以及块间进位的传播决定。通过分块和并行计算，CLA 的延迟相比 RCA 有明显的改善，尤其是当位数较大时。

• Prefix Adder 延迟 \( t_{PA} \): Prefix Adder 使用了前缀树结构，进位可以在 \( \log_2 N \) 的时间内传播，因此相较于 RCA 和 CLA，其延迟最小，尤其在 32 位或更大位宽时优势更为明显。

Subtracters & Comparators

Subtracter

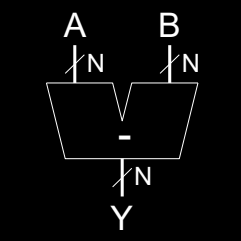
减法器的基本功能是计算两个数 \( A - B \)。在数字电路中，减法可以通过补码表示法来实现。具体来说，减法 \( A - B \) 等效于 \( A + \overline{B} + 1 \)，即将 \( B \) 取反后再加 1 来实现二进制的减法运算。

• 公式: \( A - B = A + \overline{B} + 1 \)
• 符号: 图中展示了减法器的符号表示，输入为 \( A \) 和 \( B \)，输出为结果 \( Y \)。
• 实现: 减法器通常基于加法器实现，通过取 \( B \) 的补码来执行减法。

Comparator: Equality

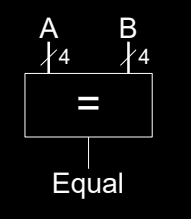
比较器用于比较两个数 \( A \) 和 \( B \) 是否相等。平等比较器的输出为 1 当且仅当 \( A = B \)，否则输出为 0。

• 符号: 使用等号符号表示，输入为 \( A \) 和 \( B \)，输出为 “Equal” 信号。
• 实现: 比较器通过比较每个位是否相等来实现，只有所有对应位相等时，输出才为 1。

Comparator: Signed Less Than

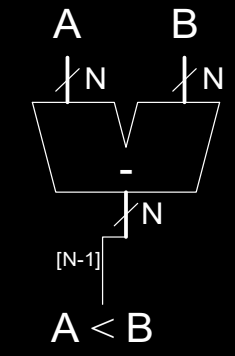
符号比较器用于判断两个有符号数 \( A \) 和 \( B \) 的大小。判断 \( A < B \) 的依据是 \( A - B \) 的结果是否为负数。当结果的最高位为 1 时，表示 \( A \) 小于 \( B \)。在进行有符号数比较时，需要特别注意溢出问题。

• 判断条件: \( A < B \) 当且仅当 \( A - B \) 为负。
• 符号: 图中展示了符号比较器的符号表示，输入为 \( A \) 和 \( B \)，输出为比较结果 \( A < B \)。
• 实现: 减法器可以用于比较器，通过计算 \( A - B \) 并检查结果的符号位来判断大小关系。

在实际设计中，符号比较器的实现需要特别考虑进位和溢出的处理，以避免错误的比较结果。

ALU: Arithmetic Logic Unit

算术逻辑单元 (ALU) 是处理器中的核心部件之一，负责执行基本的算术和逻辑运算。在数字系统中，ALU 必须能够执行以下操作：

• Addition (加法)
• Subtraction (减法)
• AND (与运算)
• OR (或运算)

ALU 控制信号

ALU 的操作由控制信号 \( ALUControl \) 来选择。通过设定不同的控制信号，ALU 能够在多个操作之间切换，例如加法、减法、逻辑与和逻辑或运算。

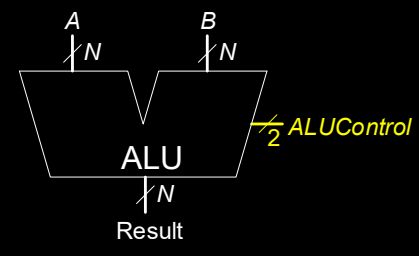
下表展示了 \( ALUControl \) 信号的不同组合及其对应的功能：

ALUControl1:0	Function
00	Add
01	Subtract
10	AND
11	OR

Example: Perform A OR B

当 \( ALUControl = 11 \) 时，ALU 执行或运算 \( A \ OR\ B \)，即将输入 A 和 B 逐位进行逻辑或操作，得到的结果作为 ALU 的输出。

• 控制信号: \( ALUControl = 11 \)
• 操作: \( Result = A \ OR \ B \)

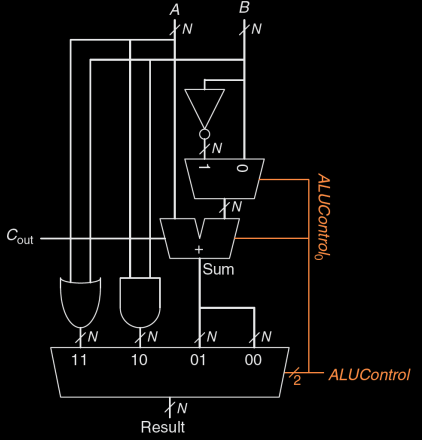
Example: Perform A + B

当 \( ALUControl = 00 \) 时，ALU 执行加法操作 \( A + B \)。在此情况下，ALU 将 A 和 B 作为加法器的输入，输出它们的和。下列步骤展示了加法的过程：

1. \( ALUControl_{1:0} = 00 \)，表明选择加法操作。
2. \( ALUControl_0 = 0 \)，加法器的进位输入 \( C_{in} \) 设为 0。加法器的第二个输入为 \( B \)，并计算出 \( A + B \)。
3. 多路复用器 (MUX) 选择加法器的输出作为最终结果。

• 控制信号: \( ALUControl = 00 \)
• 操作: \( Result = A + B \)

ALU 实现细节

在硬件实现中，ALU 包含多个子模块来分别处理加法、减法、逻辑与和逻辑或操作。根据不同的控制信号，ALU 通过多路复用器选择不同模块的输出作为最终结果。以下是主要模块的工作原理：

• 加法器: 执行二进制加法运算。
• 减法器: 通过对 B 取反并加上 1 来实现二进制减法。
• 逻辑与 (AND) 和逻辑或 (OR): 直接对 A 和 B 逐位进行相应的逻辑运算。

通过这种设计，ALU 可以灵活地在多种算术和逻辑操作之间切换，确保其适应不同的计算需求。

ALU with Status Flags

在算术逻辑单元 (ALU) 中，状态标志 (Status Flags) 用于指示运算结果的特定状态，如结果是否为负数、是否为零、是否产生进位或溢出。不同的状态标志对于后续指令的执行和判断至关重要。

ALU 状态标志

以下是常见的 ALU 状态标志：

Flag	Description
N	Result is Negative
Z	Result is Zero
C	Adder produces Carry out
V	Adder Overflowed

这些标志通过 ALU 的输出结果和运算条件来设置，并在执行加法、减法等运算时动态更新。标志的值可以用于条件跳转或决定后续计算的操作。

状态标志的实现

1. N (Negative): 当运算结果为负时，N 标志位为 1。它通过连接结果的最高有效位 (MSB) 来确定运算结果的符号。
   • 判断条件: 如果结果是负数（即最高有效位为 1），则 N = 1。
   • 实现方式：N 连接到运算结果的最高位。
2. Z (Zero): 当运算结果的所有位均为 0 时，Z 标志位为 1。
   • 判断条件: 如果结果的所有位都是 0，则 Z = 1。
   • 实现方式：通过检测结果的每一位，判断是否全为 0。
3. C (Carry out): 当加法运算产生进位时，C 标志位为 1。
   • 判断条件: 如果在最高有效位产生进位，则 C = 1。
   • 实现方式：C 通过加法器的进位输出产生。
4. V (Overflow): 当执行有符号加法或减法时，若结果超出表示范围，V 标志位为 1。
   • 判断条件: 如果加法或减法导致溢出，则 V = 1。
   • 实现方式：通过判断进位信号是否与符号位不一致来确定溢出。

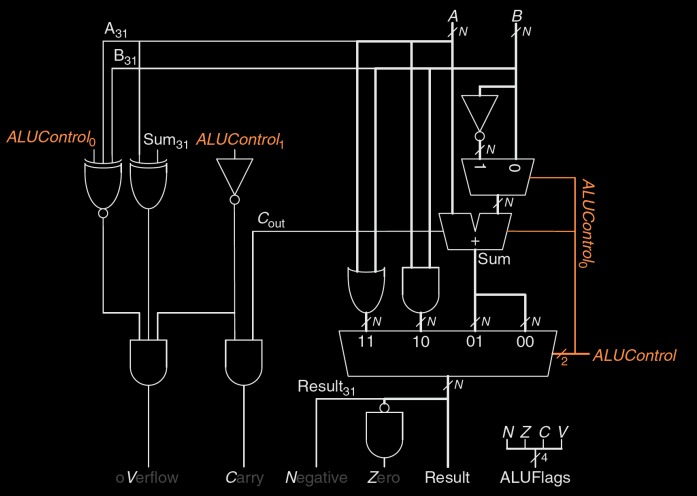
ALU with Status Flags 图示

• 在硬件设计中，ALU 不仅需要执行算术和逻辑操作，还要通过组合逻辑电路产生相应的状态标志。
• 图中展示了一个 32 位的 ALU 架构示例，ALU 执行加法、减法、与、或操作，并生成相应的状态标志 (N、Z、C、V)。
• ALUFlags 输出：N、Z、C 和 V 标志作为运算结果的附加输出，反馈给处理器的控制单元。

ALU with Status Flags: Negative

• N 标志: 当结果是负数时，N = 1。
• 连接到结果的最高有效位 (MSB)，该位决定了结果的符号。当 MSB 为 1 时，结果为负数，N 标志被置为 1。

ALU with Status Flags: Zero

• Z 标志: 当结果的所有位都为 0 时，Z = 1。
• 检查结果的所有位，如果所有位均为 0，Z 标志被置为 1，表示运算结果为零。

这些状态标志使得处理器可以基于 ALU 运算结果做出判断，例如条件跳转、分支预测等逻辑决策。

ALU with Status Flags: Carry

C (Carry) 标志位表示在加法或减法运算时，是否发生了进位或借位。

条件

• 当加法器的输出 \( C_{out} \) 为 1 时，Carry 标志位 \( C = 1 \)。
• ALU 必须执行加法或减法操作，这由 \( ALUControl \) 的值决定：
  • \( ALUControl = 00 \)（加法）
  • \( ALUControl = 01 \)（减法）

工作原理

• 在加法运算中，如果最高位产生了进位，则 \( C_{out} \) 置为 1，同时 C 标志位也会被设置为 1。
• 类似地，在减法运算中，如果需要借位，C 标志位也会被置为 1。

实现

• 图中展示了 ALU 如何通过加法器的进位输出来设置 Carry 标志。当 \( C_{out} \) 为 1 且 ALU 正在执行加法或减法时，Carry 标志就会被置为 1。

ALU with Status Flags: Overflow

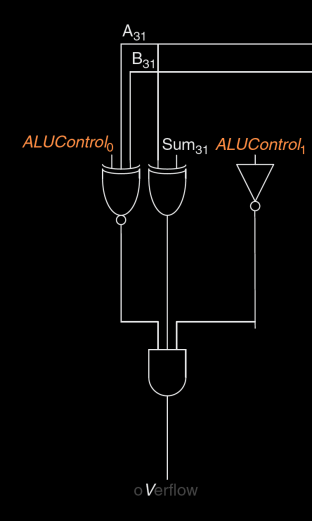
V (Overflow) 标志位用于表示有符号数的加法或减法运算中是否发生溢出。溢出发生在以下情况：

• ALU正在执行加法或减法：这个条件由 \( ALUControl_1 = 0 \) （右边非门）确定，表示ALU正在进行加法或减法操作。
• A和Sum的符号不同：这个条件是通过A的最高位 \( A_{31} \) 和Sum的最高位 \( Sum_{31} \) 的异或操作（中间异或门）实现的，即符号不同，异或的结果为1。
• A和B在加法时具有相同符号，或者在减法时具有不同符号（左边三输入同或门）：
  • 如果是加法 (\( ALUControl_0 = 0 \))，则A和B的符号（最高位 \( A_{31} \) 和 \( B_{31} \)）应该相同（000或001）；
  • 如果是减法 (\( ALUControl_0 = 1 \))，则A和B的符号应该不同（101或001）。

三输入异或门（3-input XOR Gate）

异或门（XOR Gate）输出为1的条件是其输入中1的个数为奇数。对于三输入异或门（输入A、B、C）来说，它的逻辑功能可以描述为：

• 如果A、B、C中有奇数个1，则输出为1；
• 如果A、B、C中有偶数个1，则输出为0。

三输入异或门的真值表如下：

A	B	C	输出 (XOR)
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

通过观察真值表可以看到，只有当输入为1的个数为奇数时，输出才是1。

三输入同或门（3-input XNOR Gate）

同或门（XNOR Gate）是异或门的逆，即其输出为1的条件是输入中1的个数为偶数。对于三输入同或门（输入A、B、C），其逻辑功能可以描述为：

• 如果A、B、C中有偶数个1，则输出为1；
• 如果A、B、C中有奇数个1，则输出为0。

三输入同或门的真值表如下：

A	B	C	输出 (XNOR)
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

从表中可以看出，当输入为1的个数是偶数时，输出为1。

总结

• 三输入异或门的输出为1的条件是输入中1的个数为奇数；
• 三输入同或门的输出为1的条件是输入中1的个数为偶数。

Comparison Flags for Signed and Unsigned Numbers

Comparison	Signed	Unsigned
==	Z	Z
!=	~Z	~Z
<	N ^ V	~C
<=	Z | (N ^ V)	Z | ~C
>	~Z & ~(N ^ V)	~Z & C
>=	~(N ^ V)	C

• Z (Zero): 判断两个数是否相等。
• N (Negative): 用于判断有符号数的大小比较。
• C (Carry out): 用于无符号数的进位判断。
• V (Overflow): 用于检测有符号数的溢出情况。

1. 相等（==）

• 有符号数和无符号数的条件都是 Z 标志位为1。

• 条件：当 \( A - B = 0 \) 时，Z 标志位被置为1。这表示 A 和 B 是相等的，无论它们是有符号还是无符号数。

  对于这个情况，无论有符号还是无符号，结果是：

  • A = B。

2. 不相等（!=）

• 有符号数和无符号数的条件都是 ~Z。

• 条件：当 \( A - B \neq 0 \) 时，Z 标志位为0，表示 A 和 B 不相等。

  对于这个情况，可能的结果是：

  • A > B 或 A < B。
  • 具体结果需要根据符号（有符号或无符号）进一步判断。

3. 小于（<）

有符号数的比较

• 条件：使用 \( N \oplus V \) 来判断。如果负号标志 \( N \) 和溢出标志 \( V \) 不同时，表示有符号数 \( A < B \)。

• 关键在于符号溢出。如果 \( A \) 和 \( B \) 是有符号数，溢出标志 \( V \) 反映了操作的结果是否超出了有符号数的范围。

• 情况1：\( A \) 和 \( B \) 都是正数：

  • 如果 \( A < B \)，则 \( A - B \) 为负数，设置 \( N = 1 \)，且 \( V = 0 \)。
  • 如果 \( A > B \)，则 \( A - B \) 为正数，设置 \( N = 0 \)，且 \( V = 0 \)。

• 情况2：\( A \) 和 \( B \) 都是负数：

  • 如果 \( A < B \)，则 \( A - B \) 为负数，设置 \( N = 1 \)，且 \( V = 0 \)。
  • 如果 \( A > B \)，则 \( A - B \) 为正数，设置 \( N = 0 \)，且 \( V = 0 \)。

• 情况3：\( A \) 和 \( B \) 符号不同：

  \( A \) 为负数，\( B \) 为正数

  • 减法操作：\( A - B \)。
  • 预期结果：正常情况下，负数减正数的结果应该是负数。
  • 溢出条件：如果结果出现溢出，说明减法的结果变成了正数，这与预期相反，导致设置了溢出标志 \( V = 1 \)，并且符号位 \( N = 0 \)（表示结果是正数）。
  • 判断：此时 \( N \oplus V = 1 \)，表明 \( A < B \)，即负数小于正数。

  \( A \) 为正数，\( B \) 为负数

  • 减法操作：\( A - B \)。
  • 预期结果：正数减负数应该得到正数。
  • 溢出条件：如果发生溢出，结果反而是一个负数，这与预期相反，导致设置了溢出标志 \( V = 1 \)，并且符号位 \( N = 1 \)（表示结果是负数）。
  • 判断：此时 \( N \oplus V = 0 \)，表明 \( A > B \)，即正数大于负数。

无符号数的比较

• 条件：使用 ~C 来判断，如果没有借位（即没有产生进位），则 \( A < B \)。
• 情况1：当 \( A \) 和 \( B \) 都是无符号数时：
  • 如果 \( A < B \)，则 \( A - B \) 的运算会产生借位，C 标志位会被设置为0，此时 ~C = 1，表示 \( A < B \)。
  • 如果 \( A > B \)，则 \( A - B \) 没有借位，C 标志位为1，此时 ~C = 0，表示 \( A \geq B \)。

…

Other ALU Operations

• Set Less Than (SLT): 当 \( A < B \) 时，设置结果的最低有效位 (LSB) 为 1；否则为 0。
  • 操作结果:
    • 当 \( A < B \) 时，结果为 000…001。
    • 否则，结果为 000…000。
  • 该操作有有符号数和无符号数的变体。
• XOR: 逻辑异或操作，结果为 \( A \oplus B \)。

Shifters, Multipliers, & Dividers

Shifters

移位操作是数字电路中常见的基本操作之一，主要用于左移或右移二进制数。根据移位方式的不同，移位器可以分为逻辑移位、算术移位和旋转移位。不同的移位方式对数值的影响不同，特别是在符号位和高低位的处理上。

• Logical Shifter（逻辑移位）: 逻辑移位将值向左或向右移动，空出的位用0填充。
  • 示例:
    • \( 11001 » 2 \) 结果为 \( 00110 \)
    • \( 11001 « 2 \) 结果为 \( 00100 \)
• Arithmetic Shifter（算术移位）: 算术移位类似于逻辑移位，但右移时，空出的高位填充最初的符号位（最高有效位，MSB），保持数值的符号不变。
  • 示例:
    • \( 11001 »> 2 \) 结果为 \( 11110 \)
    • \( 11001 «< 2 \) 结果与逻辑左移相同，为 \( 00100 \)
• Rotator（旋转移位）: 旋转移位将二进制位沿循环方向移动，移出的一端位被重新移入到另一端。
  • 示例:
    • \( 11001 \ ROR \ 2 \) 结果为 \( 01110 \)
    • \( 11001 \ ROL \ 2 \) 结果为 \( 00111 \)

Shifter Design

移位器的设计可以通过不同的电路结构来实现，包括逻辑移位、算术移位和旋转移位。图中展示了移位器的电路设计，通过多路复用器和控制信号选择不同的移位方式。

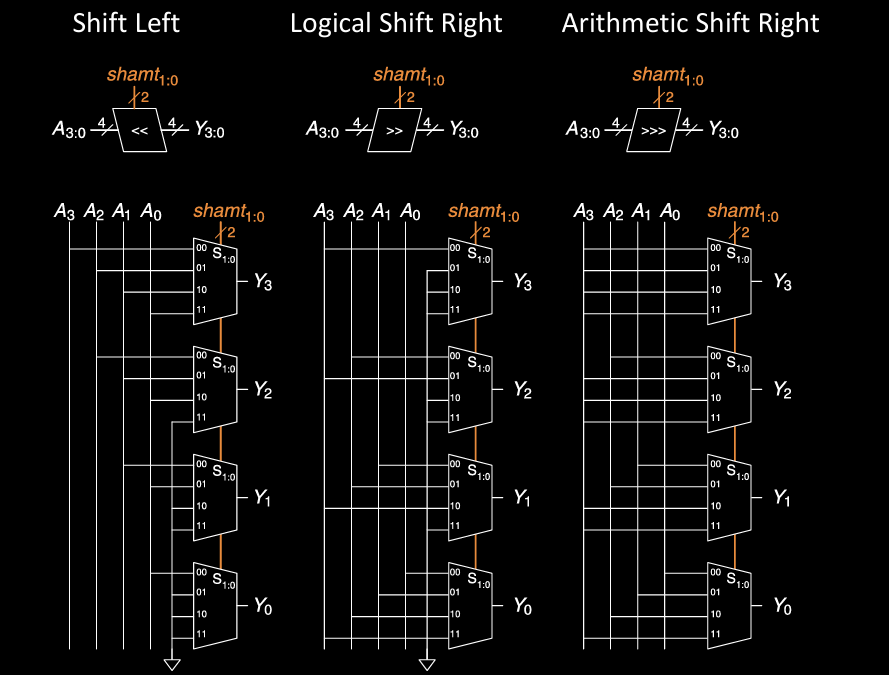
左移操作（Shift Left）

左移操作的电路结构如图左侧所示，其功能是将输入的二进制数按位左移，空出来的最低位用0填充。具体操作符为“«”，表示二进制数的各位向左移位。举例来说，假设输入的4位二进制数为 \(A_3, A_2, A_1, A_0\)，左移操作将 \(A_2\) 移到 \(Y_3\)，\(A_1\) 移到 \(Y_2\)，依次类推，\(A_0\) 移到 \(Y_1\)。最低位 \(Y_0\) 始终为0，因为左移后的空位用0填充。

这个电路中，移位的数量由 shamt_1:0 （即移位量控制信号）决定。图中显示了每个位的电路设计，其中每一行代表一个多路复用器（MUX），它根据 shamt_1:0 的值选择对应的输入值进行输出。比如，如果 shamt_1:0 为 “01”，则表示左移1位，MUX将选择输入信号中的对应位进行输出。

左移操作是通过简单的硬件移位实现，左移后的二进制数会填充0，有助于实现快速乘2的操作。

逻辑右移操作（Logical Shift Right）

中间的电路展示了逻辑右移操作，其符号为 “»”。逻辑右移的特点是将二进制数整体向右移位，并且高位填充0。对于输入的二进制数 \(A_3, A_2, A_1, A_0\)，逻辑右移1位时，\(A_3\) 移动到 \(Y_2\)，\(A_2\) 移到 \(Y_1\)，以此类推，最后一位 \(A_0\) 移动到 \(Y_0\)。

在这个设计中，同样通过多路复用器（MUX）控制移位的实现。移位量由 shamt_1:0 控制，电路会根据这个信号选择是进行0位、1位、2位还是3位的移位。例如，当 shamt_1:0 为 “01” 时，表示右移1位，因此 \(A_3\) 将输出到 \(Y_2\)，\(A_2\) 输出到 \(Y_1\)，以此类推。最右端的 \(Y_0\) 则是 \(A_0\) 的值，而最高位 \(Y_3\) 会填充0。

逻辑右移是用于将数字右移，同时将最高位用0填充，常用于无符号数的位操作中。

算术右移操作（Arithmetic Shift Right）

右侧的电路展示了算术右移操作，其符号为 “>>>”。算术右移与逻辑右移的区别在于，它保持最高位（符号位）不变，适用于有符号数的处理。通过这种方式，负数在进行右移时仍然保持符号不变。

在算术右移电路中，移位逻辑与逻辑右移类似，但有一个重要的区别：最高位 \(A_3\) 在移位时不会改变，而是直接传递到输出的最高位 \(Y_3\)，而其他位则按照移位操作正常移动。例如，\(A_2\) 移到 \(Y_2\)，\(A_1\) 移到 \(Y_1\)，依此类推，最低位 \(A_0\) 移动到 \(Y_0\)。

和前两种移位操作一样，算术右移也由 shamt_1:0 控制移位的位数，多路复用器根据移位量选择合适的输入进行输出。当 shamt_1:0 为 “01” 时，右移1位，最高位保持不变，其余位按序右移。

算术右移通常用于有符号数的右移操作，确保负数符号位的正确传递，在处理补码表示的有符号数时非常有用。

Shifters as Multipliers and Dividers

移位操作不仅用于基本的位移操作，还可以用于实现快速的乘法和除法运算。通过移位运算，可以将一个数乘以或除以 2 的幂，从而实现高效的计算。

• 左移作为乘法器: 左移 \( A << N \) 等同于将 \( A \) 乘以 \( 2^N \)。
  • 公式: \( A << N = A \times 2^N \)
• 右移作为除法器: 算术右移 \( A >>> N \) 等同于将 \( A \) 除以 \( 2^N \)。
  • 公式: \( A >>> N = A \div 2^N \)

通过这些位移操作，可以快速实现数值的乘法和除法运算，而无需复杂的乘法器或除法器硬件。

Multipliers

乘法器通过将乘数的每一位与被乘数相乘来生成部分积，然后将这些移位后的部分积相加，得到最终的乘法结果。在数字电路中，乘法运算可以使用加法器和移位器的组合实现。

Partial Products (部分积)

• 部分积：将乘数的每一位分别与被乘数相乘，生成多个部分积。每个部分积都相当于被乘数乘以乘数的一位。
• 移位相加：所有部分积根据其对应的位移位数进行移位，然后相加得到最终结果。

例子

• 十进制:
  • 乘数：230， 被乘数：42
  • 部分积：230 × 2 = 460，230 × 4（左移一位）= 920
  • 结果：9660
• 二进制:
  • 乘数：\( 0101 \)（5），被乘数：\( 0111 \)（7）
  • 部分积：\( 0101 \times 1 = 0101 \)，\( 0101 \times 1 = 0101 \)（左移一位），最后相加结果为 \( 00100011 \)（35）

4x4 Multiplier

4x4 乘法器是一个基本的硬件乘法器，它可以处理 4 位乘数和 4 位被乘数的乘法运算。

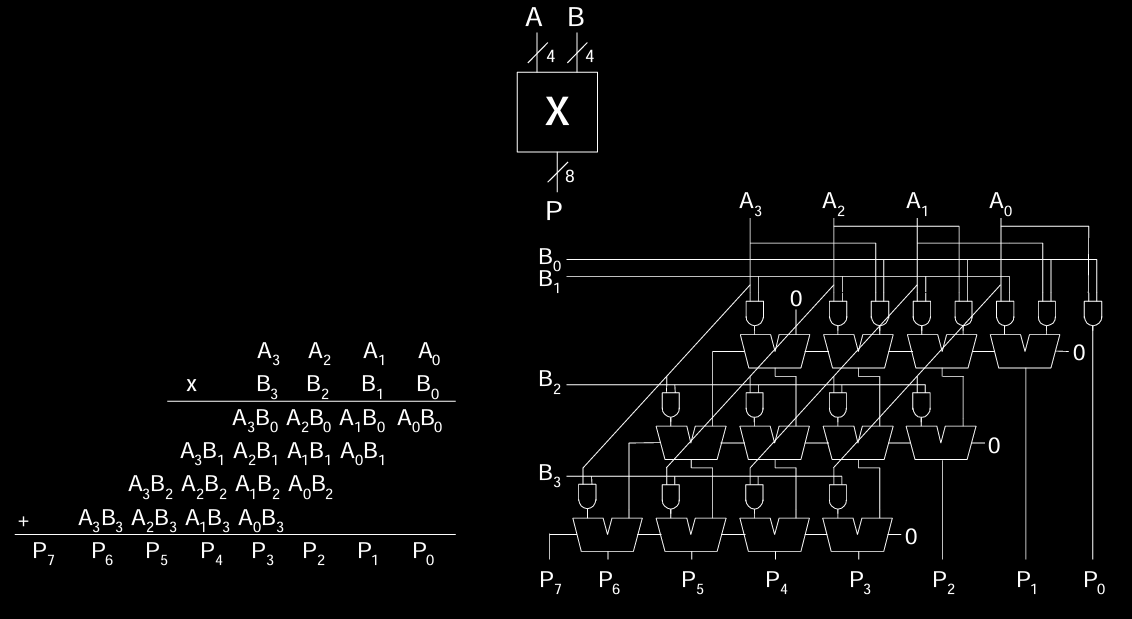
4x4二进制乘法器实现了两个4位二进制数之间的乘法操作，并将结果输出为8位数。图中展示了一个典型的4x4乘法器电路，包括乘法的步骤及其对应的硬件实现。

数学乘法过程

在二进制系统中，乘法与十进制相似，只是进位规则不同。我们来看两个4位二进制数 \(A_3A_2A_1A_0\) 和 \(B_3B_2B_1B_0\) 的乘法运算。与十进制乘法一样，我们依次用 \(B_0\), \(B_1\), \(B_2\), \(B_3\) 乘以 \(A_3A_2A_1A_0\)，并将每一步得到的结果进行移位累加。

1. 第一步：用 \(A_3A_2A_1A_0\) 乘以 \(B_0\)，这相当于 \(A_3B_0, A_2B_0, A_1B_0, A_0B_0\)，产生一组部分积（Partial Products），这些结果直接作为乘法的最低位结果。

2. 第二步：用 \(A_3A_2A_1A_0\) 乘以 \(B_1\)，并向左移1位。相当于将 \(A_3B_1, A_2B_1, A_1B_1, A_0B_1\) 移位后相加。

3. 第三步：用 \(A_3A_2A_1A_0\) 乘以 \(B_2\)，并向左移2位。

4. 第四步：用 \(A_3A_2A_1A_0\) 乘以 \(B_3\)，并向左移3位。

每一步的部分积都需要与前一步的结果进行累加，最终得到8位的乘积 \(P_7P_6P_5P_4P_3P_2P_1P_0\)。

硬件电路实现

右侧展示了实现这一乘法运算的硬件结构，这个电路通过与门（AND gates）和加法器（Full Adders）来实现4x4乘法。

1. 与门（AND Gates）

乘法器的基础构件是与门，每个与门对应一个部分积的计算。在每一行中，二进制数 \(A_3A_2A_1A_0\) 分别与 \(B_3, B_2, B_1, B_0\) 相与，生成部分积。例如，第一行的与门产生的结果是 \(A_3B_0, A_2B_0, A_1B_0, A_0B_0\)，这些就是我们数学过程中的部分积。每个与门的输出接到加法器的输入端，参与后续的累加操作。

2. 移位与累加

在进行部分积累加时，电路需要将这些部分积逐步移位，这通过连接线的布置实现。具体来说，第二行的部分积向左移1位，第三行的部分积向左移2位，第四行的部分积向左移3位。这样做模拟了十进制乘法中对每一步结果的对位相加。

3. 加法器（Full Adders）

加法器的作用是将这些移位后的部分积累加起来。每个加法器接收来自两个与门的输出，进行二进制加法运算，并将进位传递给下一位。加法器通过层层传递进位，最终生成乘法结果的每一位。例如，最低位 \(P_0\) 是直接由 \(A_0B_0\) 产生的，而 \(P_1\) 则是 \(A_1B_0\) 与 \(A_0B_1\) 的和，依此类推。

4. 乘积输出

最终，经过四层累加操作，电路将产生8位的乘法结果，分别是 \(P_7P_6P_5P_4P_3P_2P_1P_0\)。这些结果可以表示为二进制数，代表 \(A\) 和 \(B\) 的乘积。

Dividers

除法器用于在硬件中实现除法运算，通过计算商 (Quotient, Q) 和余数 (Remainder, R)。除法的结果可以表示为：

\[ A / B = Q + R / B \]

这意味着：被除数 \( A \) 除以除数 \( B \) 得到商 \( Q \) 和余数 \( R \)，其中余数满足 \( R < B \)。

Decimal Example

以十进制为例：

• 被除数：2584
• 除数：15
• 结果：2584 / 15 = 172 余 4

Long-Hand Division (十进制长除法)

在十进制长除法中，步骤如下：

1. 将被除数逐位除以除数，得到部分商。
2. 将每次除法后的余数与下一位被除数结合，继续进行下一次除法。
3. 重复该过程，直到所有位数除完，得到最终商和余数。

如例子所示：

• 第一步：2584 ÷ 15 = 172，余数为 4。
• 通过长除法的步骤，最终结果为 172 余 4。

Binary Example (二进制除法)

在二进制除法中，步骤与十进制类似：

• 被除数：1101（二进制的 13）
• 除数：0010（二进制的 2）
• 结果：1101 ÷ 0010 = 0110，余数为 1。

步骤如下：

1. 将被除数的高位逐位与除数比较，如果大于或等于除数，则商的当前位为 1，并进行减法计算余数。
2. 如果小于除数，则商的当前位为 0，余数保持不变。
3. 继续处理下一位，直到所有位都处理完毕。

最终结果为商 \( 0110 \)（即十进制的 6），余数为 \( 1 \)。

Division Algorithm in Hardware

硬件中的除法运算可以通过移位和减法来实现。基本过程如下：

1. 初始化余数 \( R’ = 0 \)。
2. 从被除数的最高位开始，逐位将被除数移位并与当前余数 \( R \) 结合。
3. 将当前余数减去除数，如果差值为负，则商的当前位为 0；如果为正，则商的当前位为 1，并将差值作为新的余数。
4. 继续进行直到所有位处理完毕，最终得到商 \( Q \) 和余数 \( R \)。

如图所示：

• 在二进制除法 \( 1101 ÷ 10 \) 中，结果为商 \( 0110 \) 和余数 \( R = 1 \)。

通过移位和减法的组合，硬件可以高效地执行除法运算。

4x4 Divider

4x4二进制除法器实现了两个4位二进制数的除法运算，输出商（Quotient）和余数（Remainder）。该电路基于逐步减法的方式来完成除法操作，每一行对应除法算法的一次迭代。通过对被除数（Dividend）和除数（Divisor）的处理，电路最终输出商 \(Q_3Q_2Q_1Q_0\) 和余数 \(R_3R_2R_1R_0\)。接下来，我们将分析除法器的工作原理以及电路结构。

除法算法的概述

除法器的核心算法基于移位和减法的组合。右侧展示了这一算法的伪代码，概述了计算步骤：

1. 初始条件：将余数寄存器 \(R’\) 初始化为0。被除数 \(A_3A_2A_1A_0\) 从最高位开始依次进入运算。

2. 迭代运算：从最高位开始，依次进行移位和减法运算：
   • 先将 \(R’\) 左移一位，并将当前被除数位 \(A_i\) 追加到 \(R’\) 的最低位，构成新的 \(R\)。
   • 将 \(R\) 减去除数 \(B\)，得到差值 \(D\)。
   • 如果差值 \(D\) 小于0，说明除不尽，此时商位 \(Q_i = 0\)，余数 \(R’\) 不变，保留原值。
   • 如果差值 \(D\) 大于等于0，说明除得尽，此时商位 \(Q_i = 1\)，并更新余数 \(R’ = D\)。
3. 最终结果：经过每一位的处理后，商和余数分别存储在 \(Q_3Q_2Q_1Q_0\) 和 \(R_3R_2R_1R_0\) 中。

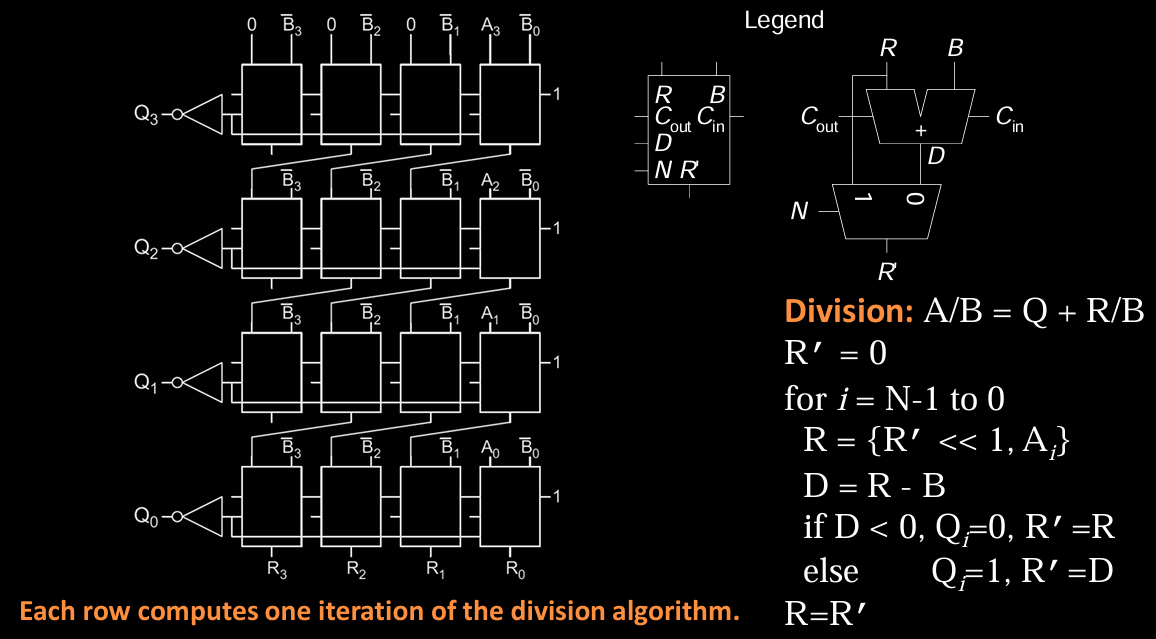
电路结构解析

左侧的电路图展示了4x4除法器的硬件实现。电路中每一行表示一次迭代操作，即从最高位到最低位的除法运算。每行的结构基本相同，通过移位、减法和判断逻辑完成该位的除法操作。

1. 加法器/减法器（ALU）

每个方框表示一个右上角的加法器（ALU）和二路选择器（Multiplexer）的组合，它接收当前的余数 \(R\) 和除数 \(B\)，并计算出 \(D = R - B\)。二路选择器根据减法结果选择新的余数。如果减法成功（\(D \geq 0\)），则更新余数为 \(R’ = D\)；否则保持原余数不变。

在每一行的操作中，被除数的当前位 \(A_i\) 通过移位器进入运算，并与之前计算得到的余数一起构成新的 \(R\)。接下来，重复减法器计算 \(R - B\)，并通过逻辑判断 \(D\) 是否小于0。

2. 判断商的位值

每一行的运算都会决定当前商位 \(Q_i\) 的值。减法操作得到差值 \(D\) 后，如果 \(D < 0\)，表示本次除法不足，此时 \(Q_i = 0\)，并将原余数保留不变；如果 \(D \geq 0\)，则表示本次除法足够，商位 \(Q_i = 1\)，并将新的余数 \(R’ = D\) 更新。

3. 余数的移位与更新

在每一轮迭代开始前，余数寄存器 \(R’\) 会先左移一位，以便为当前位的被除数 \(A_i\) 腾出位置。这一操作通过移位器实现，将上一轮计算的余数进行移位后，追加当前被除数位 \(A_i\) 形成新的 \(R\)。该余数随后参与减法运算，并根据计算结果进行更新或保持不变。

4. 最终输出

电路经过4次迭代后，最终会在商寄存器 \(Q_3Q_2Q_1Q_0\) 中得到除法的商，在余数寄存器 \(R_3R_2R_1R_0\) 中得到除法的余数。这些寄存器的值对应于完整的除法操作结果。

加法器与二路选择器

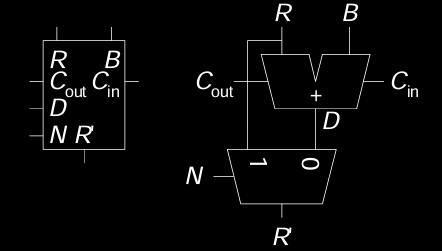
右上角的加法器（ALU）和二路选择器（Multiplexer）的组合单元负责处理每一行的运算，具体来说，它执行移位后的被除数与除数的减法操作，并根据结果选择相应的输出值。我们可以进一步详细分析这个组合单元的作用。

1. 加法器/减法器（ALU）

右上角图中的加法器实际上是一个可执行加法和减法的运算单元。它有四个输入端：

• \(R\)：当前的余数或之前的计算结果。
• \(B\)：除数。
• \(C_{\text{in}}\)：进位输入，通常在减法运算中使用。
• \(D\)：减法结果 \(R - B\)。

加法器在执行减法时，会将余数 \(R\) 与除数 \(B\) 相减，计算出结果 \(D\)。这个减法操作是每一行的核心部分，它决定了当前商位是否为1，也影响了下一轮迭代中的余数。

2. 二路选择器（Multiplexer）

加法器旁边的二路选择器负责在两种可能的结果之间进行选择。选择器有两个主要输入：

• \(R\)：当前的余数（或者说，上一轮运算中未能完全减去的部分）。
• \(R’ = D\)：加法器计算出的新余数，即减法操作的结果。

二路选择器根据减法结果 \(D\) 的符号来选择输出：

• 如果 \(D \geq 0\)，说明被除数可以被除数 \(B\) 减去，因此选择 \(R’ = D\)，更新余数。
• 如果 \(D < 0\)，表示当前被除数位不足以完成一次有效的减法操作，此时选择保留原来的余数 \(R\)，继续下一轮运算。

3. 商位判断（Quotient Decision）

在每一行的运算中，商位 \(Q_i\) 的值也通过这个组合电路产生。具体来说：

• 当 \(D \geq 0\) 时，除法运算可以进行，商位 \(Q_i = 1\)。
• 当 \(D < 0\) 时，无法完成有效的减法操作，商位 \(Q_i = 0\)。

商位的值通过二路选择器的选择逻辑产生，并在每轮计算中决定当前位的商是否为1。

Fixed-Point Numbers

定点数

在数字系统中，定点数用于表示带有小数的数值。与浮点数不同，定点数的小数点（或称二进制点）位置是固定的。它通常用于嵌入式系统或处理器中，以实现更高效的数值计算，尤其是在硬件资源有限的情况下。

Number Systems

在二进制系统中，我们可以表示：

• 正数: 通过无符号二进制表示。
• 负数: 通过补码或符号/数值表示。

那么，如何表示小数呢？

Numbers with Fractions

表示小数的两种常见方法是：

• Fixed-point (定点数): 二进制小数点的位置是固定的，预先约定好整数位和小数位的数量。
• Floating-point (浮点数): 二进制小数点的位置是浮动的，它会根据最重要的一位（最高有效位）的位置移动。

Fixed-Point Numbers

定点数通过预定义的位数来表示整数部分和小数部分。例如，使用 4 位整数部分和 4 位小数部分来表示数值 6.75 的二进制表示：

• 二进制表示: \[ 0110.1100 \] 其中小数点前的 \( 0110 \) 表示整数 6，小数点后的 \( 1100 \) 表示小数部分。

• 解析: \[ 6.75 = 2^2 + 2^1 + 2^{-1} + 2^{-2} \]

• 注意:

  • 二进制点的存在是隐含的（没有明确表示出来）。
  • 必须预先约定好整数位和小数位的数量，以确保数值的正确解释。

定点数的主要优势在于它能够使用较少的硬件资源进行小数运算，并且避免了浮点数计算中复杂的格式转换。

Unsigned Fixed-Point Formats

在无符号定点数格式中，使用固定数量的位来表示整数部分和小数部分。格式为 \( Ua.b \)，其中：

• a: 表示整数部分的位数。
• b: 表示小数部分的位数。

例子：表示 6.75

不同的定点数格式可以用不同数量的整数和小数位表示 6.75。例如：

• U4.4: \( 01101100 \)
  • 4 位整数，4 位小数
• U3.5: \( 11011000 \)
  • 3 位整数，5 位小数
• U6.2: \( 00011011 \)
  • 6 位整数，2 位小数

常见位宽

• 8, 16, 和 32 位定点数是常见的表示形式。
• U8.8: 常用于传感器数据、音频和像素表示。
• U16.16: 提供更高精度，常用于信号处理。

Signed Fixed-Point Formats

有符号定点数使用补码表示法，其中第一个位是符号位。格式为 \( Qa.b \)，其中：

• a: 表示整数部分（包括符号位）。
• b: 表示小数部分。

定点数取反

将有符号定点数取反的方法：

1. 将所有位取反。
2. 在最低有效位 (LSB) 上加 1。

例子：表示 -6.75 在 Q4.4 中

• 原值 6.75: \( 01101100 \)
• 取反: \( 10010011 \)
• 加 1: \( 10010100 \)

常见格式

• Q1.15（也称为 Q15）常用于信号处理，用于表示 \( [-1, 1) \) 的范围。

Saturating Arithmetic（饱和算术）

溢出在定点数运算中通常是有害的，可能会产生不期望的结果，例如：

• 视频: 高亮像素中的黑点。
• 音频: 点击声。

饱和算术

饱和算术是一种防止溢出的方法，在发生溢出时，将结果限制为可能的最大值，而不是循环回去。

例子

在 \( U4.4 \) 中：

• 运算: \( 11000000 \)（12） + \( 01111000 \)（7.5） = \( 11111111 \)。
• 结果: 15.9375，不发生溢出，而是取最大可能值。

饱和算术通过限制溢出避免了数值计算中的失真或错误结果。

Floating-Point Numbers

浮点数

浮点数的表示方式类似于科学计数法，数值的二进制小数点可以“浮动”，它的位置取决于最重要的 1。浮点数允许表示非常大或非常小的数值，具有更大的动态范围。

科学计数法与浮点数

浮点数的表示方式类似于十进制的科学计数法。例如，十进制数 273 可以表示为：

\[ 273 = 2.73 \times 10^2 \]

浮点数的通用形式为：

\[ \pm M \times B^E \]

其中：

• M：尾数（Mantissa）
• B：基数（Base），通常为 2
• E：指数（Exponent）

例如，数值 273 的表示为：

• \( M = 2.73 \)
• \( B = 10 \)
• \( E = 2 \)

Floating vs. Fixed Point Numbers

浮点数与定点数的主要区别如下：

• 浮点数类似于科学计数法，允许表示更大的动态范围（从最小到最大的数值）。
  • 计算复杂度更高，因为在执行加法或减法运算时，尾数需要对齐，这增加了性能和功耗的开销。
• 定点数在程序员层面更复杂，因为它需要处理较小的动态范围以及溢出问题。
  • 适合信号处理，当需要高性能和低功耗时使用，例如机器学习、视频处理等。
• 浮点数的优势在于更适合通用计算，特别是在编程效率优先的情况下。
• 定点数的优势在于硬件性能优先时，特别是在信号处理、机器学习中，定点数通常效率更高。

Floating-Point Representation

在浮点数表示中，通常采用 IEEE 754 标准，该标准定义了浮点数的结构。在 32 位浮点数中，格式如下：

• 1 位：符号位（Sign）
• 8 位：指数（Exponent）
• 23 位：尾数（Mantissa）

浮点数表示是一种科学计数法的二进制版本，广泛用于计算机中表示具有大动态范围的数值。下面是将十进制数 \( 228_{10} \) 转换为 IEEE 754 32 位浮点数的过程。

Step 1: Convert Decimal to Binary

将十进制数 \( 228_{10} \) 转换为二进制：

\[ 228_{10} = 11100100_2 \]

Step 2: Write in Binary Scientific Notation

将二进制数 \( 11100100_2 \) 写成二进制科学计数法的形式：

\[ 11100100_2 = 1.11001_2 \times 2^7 \]

• 尾数 \( M \) = \( 1.11001_2 \)
• 指数 \( E \) = 7

Step 3: Fill in Each Field of the 32-bit Floating Point Number

浮点数的 32 位格式由 3 部分组成：

• 1 位符号位 (Sign bit)：确定数值的正负。\( 228_{10} \) 为正数，因此符号位为 0。
• 8 位指数 (Exponent)：表示指数，偏移（bias）后存储。
• 23 位尾数 (Mantissa)：表示尾数的小数部分，隐含第一个 1。

Floating-Point Representation 2: Implicit Leading 1

在 IEEE 754 浮点数标准中，尾数的首位始终为 1，因此这个 1 不需要存储，称为隐含的 1。因此，尾数的 23 位字段只存储小数部分：

\[ 1.11001_2 \Rightarrow \text{尾数字段：} 11001000000000000000000 \]

Floating-Point Representation 3: Biased Exponent

IEEE 754 浮点数标准使用带偏移量的指数表示法。偏移量为 127，因此存储的指数为：

\[ \text{偏移指数} = 127 + 7 = 134 \]

将 134 转换为二进制：

\[ 134_{10} = 10000110_2 \]

Final IEEE 754 32-bit Floating-Point Representation

根据上述信息，\( 228_{10} \) 的最终 IEEE 754 32 位浮点数表示如下：

• 符号位：0
• 指数：10000110
• 尾数：11001000000000000000000

因此，完整的表示为：

\[ 0\ 10000110\ 11001000000000000000000 \]

Hexadecimal Representation

将其转换为十六进制表示：

\[ 0x43640000 \]

这就是数值 \( 228_{10} \) 的 32 位 IEEE 754 浮点数表示法。

Floating-Point Example

以下是将十进制数 -58.25 转换为 IEEE 754 32 位浮点数的步骤。

Step 1: Convert Decimal to Binary

将 58.25 转换为二进制： \[ 58.25_{10} = 111010.01_2 \]

Step 2: Write in Binary Scientific Notation

将二进制数 \( 111010.01_2 \) 写成科学计数法形式： \[ 1.1101001_2 \times 2^5 \]

• 尾数 \( M = 1.1101001 \)
• 指数 \( E = 5 \)

Step 3: Fill in the IEEE 754 Fields

• 符号位（Sign bit）：负数，符号位为 1。
• 指数（Exponent bits）：计算指数偏移量。偏移指数为 \( 127 + 5 = 132 \)，转换为二进制为 \( 10000100_2 \)。
• 尾数（Mantissa bits）：存储小数部分 \( 1101001 \)，补零至 23 位。

最终的浮点数表示

\[ 1\ 10000100\ 11010010000000000000000 \] 对应的十六进制表示为： \[ 0xC2690000 \]

Floating-Point Special Cases

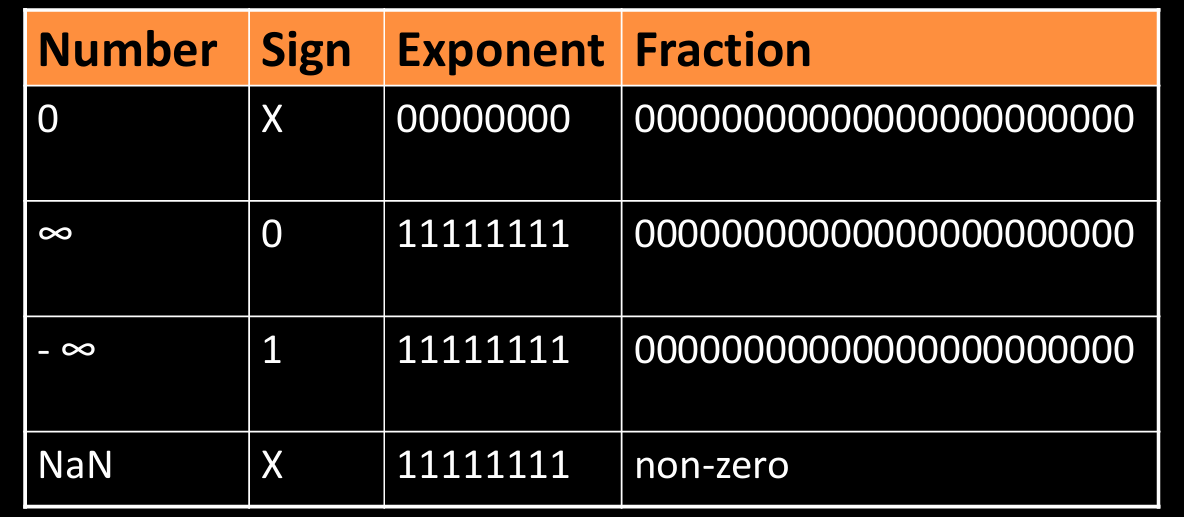
浮点数标准中还定义了几种特殊情况：

• 0: 指数和尾数全为 0，符号位为 0 或 1。
• 无穷大: 指数为全 1，尾数全为 0。
  • 正无穷：符号位为 0。
  • 负无穷：符号位为 1。
• NaN（非数值）: 指数为全 1，尾数不为 0。

Floating-Point Precision

浮点数精度有两种常见格式：

• 单精度 (Single-Precision)：
  • 32 位
  • 1 位符号位，8 位指数，23 位尾数
  • 偏移量为 127
• 双精度 (Double-Precision)：
  • 64 位
  • 1 位符号位，11 位指数，52 位尾数
  • 偏移量为 1023

Floating-Point Rounding & Overflow

浮点数表示过程中，可能会出现溢出和舍入的情况：

Overflow & Underflow

• 溢出 (Overflow)：数值过大，超出浮点数能表示的范围。
• 下溢 (Underflow)：数值过小，接近零，无法精确表示。

舍入模式

常见的舍入模式包括：

• 向下舍入
• 向上舍入
• 向零舍入
• 四舍五入（最接近的值）

Example: Rounding 1.100101 (1.578125) to 3 Fraction Bits

• 向下舍入: 1.100
• 向上舍入: 1.101
• 向零舍入: 1.100
• 四舍五入: 1.101 (1.625 更接近 1.578125)

Floating-Point Addition

浮点数加法

浮点数加法是一种复杂的运算，因为需要考虑尾数和指数的调整过程。加法过程的主要步骤如下：

1. Extract exponent and fraction bits（提取指数和小数位）
   首先，从两个待加的浮点数中提取出它们的指数和小数位。这两部分分别代表数值的大小和精度。

2. Prepend leading 1 to form mantissa（添加隐含的 1 构成尾数）
   浮点数表示中，尾数的首位始终隐含为 1，所以我们需要在小数位前加上隐含的 1，形成完整的尾数。

3. Compare exponents（比较指数）
   将两个浮点数的指数进行比较，确定哪个数的指数较大。这一步是为了对齐两个数，使它们的尾数在相同的量级上进行计算。

4. Shift smaller mantissa if necessary（如果必要，移动较小的尾数）
   对于指数较小的那个数，需要将其尾数右移，使它与指数较大的数保持相同的指数。这一步通过右移尾数实现，保证在同一位数范围内进行加法运算。

5. Add mantissas（尾数相加）
   将两个对齐后的尾数相加。这是浮点加法的核心步骤，类似于定点数的加法。

6. Normalize mantissa and adjust exponent if necessary（归一化尾数并调整指数）
   如果尾数相加的结果超过了可表示范围，可能需要对结果进行归一化调整。归一化是指通过调整尾数和指数的关系，确保尾数的首位为 1。

7. Round result（对结果进行舍入）
   由于浮点数的尾数位数有限，可能无法精确表示相加后的所有位。这时需要进行舍入，选择适当的舍入方式以减少精度损失。

8. Assemble exponent and fraction back into floating-point format（将指数和小数重新组合成浮点数格式）
   最后，将调整好的尾数和指数重新组合，形成最终的浮点数表示。

浮点加法通过这些步骤完成，在硬件或软件实现时，尤其是处理数值级别的对齐和归一化时，可能会消耗较多的资源和时间。

Floating-Point Addition Example 浮点加法示例

Step 1: Extract Exponent and Fraction Bits

首先，提取两个浮点数的符号位、指数和小数部分（尾数）的二进制表示。

• 数值 N1: 0x3FC00000
  • 符号位 \( S = 0 \)（正数）
  • 指数 \( E = 127 \)
  • 尾数 \( F = 0.10000000000000000000000 \)
• 数值 N2: 0x40500000
  • 符号位 \( S = 0 \)（正数）
  • 指数 \( E = 128 \)
  • 尾数 \( F = 0.10100000000000000000000 \)

Step 2: Prepend Leading 1 to Form Mantissa

在标准的 IEEE 754 表示中，尾数的第一位为隐含的 1。我们将其加到小数位前以形成完整的尾数：

• N1: \( 1.1_2 \)
• N2: \( 1.101_2 \)

Step 3: Compare Exponents

比较两个数的指数：

• \( 127 - 128 = -1 \)，因此需要将 N1 的尾数右移一位，以对齐指数。

Step 4: Shift Smaller Mantissa if Necessary

将 N1 的尾数右移一位，以匹配 N2 的指数：

• N1 的尾数 \( 1.1_2 \) 右移后变为 \( 0.11_2 \)，并乘以 \( 2^1 \)。

Step 5: Add Mantissas

对齐后，两个尾数相加： \[ 0.11_2 \times 2^1 + 1.101_2 \times 2^1 = 10.011_2 \times 2^1 \]

Step 6: Normalize Mantissa and Adjust Exponent if Necessary

对尾数进行归一化处理： \[ 10.011_2 \times 2^1 = 1.0011_2 \times 2^2 \] 归一化后，尾数变为 \( 1.0011_2 \)，指数增加 1，变为 \( E = 129 \)。

Step 7: Round Result

此时，结果无需舍入，因为尾数完全可以适应 23 位的尾数字段。

Step 8: Assemble Exponent and Fraction Back into Floating-Point Format

将符号位、指数和尾数重新组合，得到最终的浮点数：

• 符号位 \( S = 0 \)
• 指数 \( E = 129 \)，二进制为 \( 10000001_2 \)
• 尾数 \( F = 00110000000000000000000 \)

最终结果的浮点数表示为： \[ 0\ 10000001\ 00110000000000000000000 \] 对应的十六进制为： \[ 0x40980000 \]

Counters & Shift Registers

计数器和移位寄存器

Counters

计数器（Counters）是用于在每个时钟沿上递增数值的数字电路组件。它们常用于循环遍历一系列数字。比如，二进制计数器会循环计数如下的数列：

\[ 000, 001, 010, 011, 100, 101, 110, 111, 000, 001, … \]

计数器的典型用途

• 数字时钟显示：例如，秒、分钟、小时计数器
• 程序计数器（Program Counter）：用于跟踪当前正在执行的指令地址

计数器的符号与实现

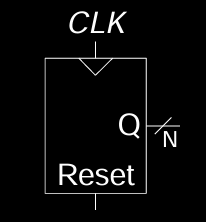
• Symbol: 图中的符号显示了带有复位（Reset）和时钟（Clock）输入的计数器。输出 \( Q \) 表示计数器当前的值，当复位信号有效时，计数器被重置。
• Implementation: 在实际硬件实现中，计数器通常由触发器和加法器组成，响应时钟信号，定期增加输出值。

Counter SystemVerilog Idiom

计数器的 SystemVerilog 代码实现展示了如何通过硬件描述语言来编写一个简单的计数器模块。在代码中，当时钟沿上升时，计数器的值递增或复位。两种不同的编写风格展示了计数器的设计：

1. 简洁的实现

module counter(input logic clk, reset,
               output logic [7:0] q);

  always_ff @(posedge clk)
    if (reset) q <= 0; // 同步复位
    else q <= q + 1;   // 计数器递增
end

该代码使用 always_ff 块监视时钟上升沿。如果复位信号有效，则计数器置零，否则递增计数器。

2. 更详细的实现

module counter(input logic clk, reset,
               output logic [7:0] q);

  logic [7:0] nextq;

  assign nextq = q + 1; // 加法器逻辑
  always_ff @(posedge clk) // 状态寄存器，带同步复位
    if (reset) q <= 0;
    else q <= nextq;
end

这个更详细的版本显示了如何通过独立的加法器和状态寄存器来实现同样的功能。nextq 保存了下一次更新的计数器值，在每个时钟沿到达时更新 q 的状态。

这些计数器模块展示了如何在数字电路设计中利用硬件描述语言高效实现计数逻辑。

以下是两个版本的 Verilog 实现：

1. 简洁的实现 (Verilog 版本)

module counter(input clk, reset,
               output reg [7:0] q);

  always @(posedge clk) begin
    if (reset)
      q <= 8'b0; // 同步复位，计数器置零
    else
      q <= q + 1; // 计数器递增
  end
endmodule

2. 更详细的实现 (Verilog 版本)

module counter(input clk, reset,
               output reg [7:0] q);

  wire [7:0] nextq;

  assign nextq = q + 1; // 加法器逻辑

  always @(posedge clk) begin // 状态寄存器，带同步复位
    if (reset)
      q <= 8'b0;
    else
      q <= nextq;
  end
endmodule

1. 简洁的实现：
   • 在 Verilog 中使用 reg 类型来存储状态（即 q），并使用 always 块监听时钟的上升沿。
   • 如果 reset 有效，计数器置零；否则，计数器递增。
2. 更详细的实现：
   • nextq 是一个 wire，它保存了 q + 1 的结果。
   • always 块在时钟上升沿时更新 q 的值。如果 reset 有效，q 被设置为0，否则更新为 nextq 的值。

Divide-by-2^N Counter

Divide-by-\(2^N\) 计数器 是一种通过计数器实现频率分频的电路，通常用于将时钟信号减慢到较低频率的输出信号。

主要特性：

• N 位计数器的最高有效位（MSB） 在每 \(2^N\) 个时钟周期内翻转一次。这意味着经过 \(2^N\) 个时钟周期，最高位输出将改变它的状态（0到1或1到0）。
• 用途：非常适合用于时钟信号的降频。例如，用于控制 LED 的闪烁频率。

例子：

• 输入时钟频率为 50 MHz，使用一个 24位 计数器。
• 最高位（MSB）每 \(2^{24}\) 个时钟周期翻转一次，这意味着输出频率为： \[ \frac{50\text{ MHz}}{2^{24}} \approx 2.98 \text{ Hz} \] 这个信号可以用于非常慢的周期性输出，如驱动LED闪烁。

数字控制振荡器（Digitally Controlled Oscillator）

数字控制振荡器 通过在每个时钟周期增加一个特定的值 \(p\) 来控制输出频率，与简单的二进制计数器不同，它不仅加1，还可以加任意值 \(p\)。这种方法允许更精确地调整输出频率。

主要特性：

• N位计数器 在每个时钟周期内增加 \(p\)，而不是简单地加1。
• 最高有效位（MSB）根据下式在频率 \(f_{out}\) 上翻转： \[ f_{out} = f_{clk} \times \frac{p}{2^N} \]

例子：

• 时钟频率 \(f_{clk} = 50 \text{ MHz}\)，目标输出频率 \(f_{out} = 200 \text{ Hz}\)。
• 为了得到目标频率，必须确定适当的 \(p\) 和 \(N\)，满足公式： \[ \frac{p}{2^N} = \frac{200}{50 \times 10^6} \]
• 设 \(N = 24\)，则 \(p = 67\)，对应的输出频率 \(f_{out} \approx 199.676 \text{ Hz}\)。
• 或者，设 \(N = 32\)，则 \(p = 17179\)，对应的输出频率 \(f_{out} \approx 199.990 \text{ Hz}\)。

Shift Registers

移位寄存器

移位寄存器 是一种可以在每个时钟周期内向左或向右移动数据位的寄存器结构。它们常用于将串行输入转换为并行输出，或者反过来，依赖于时钟信号进行数据的逐位移动。

• 工作方式：
  • 每个时钟边沿，输入一个新位（从 \( S_{in} \) 进入），将所有存储位向右移位，输出一个旧位（从 \( S_{out} \) 移出）
• 应用场景：
  • 串行到并行转换器：将串行输入 \( S_{in} \) 逐位移入，并在寄存器中依次存储转换为并行输出 \( Q_{0:N-1} \)

移位寄存器的符号和实现

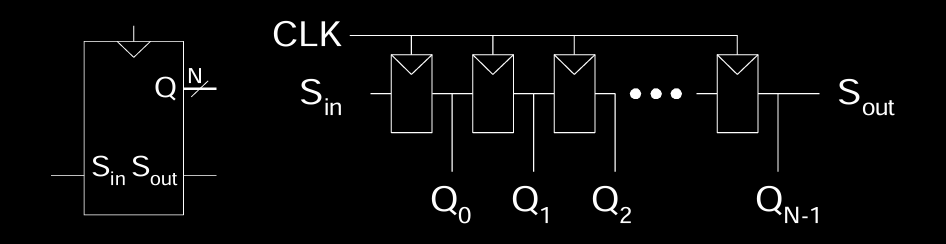
• Symbol：图示中的符号展示了移位寄存器的功能，其中有时钟输入 \( CLK \) 和数据输入 \( S_{in} \)，数据从 \( S_{out} \) 移出。
• Implementation：移位寄存器由多个 D 触发器连接而成，每个触发器在时钟沿到达时保存并移位一个位，触发器的输入是前一个触发器的输出，从而实现逐位的移位操作。

这种结构在通信系统中广泛应用，用于串行通信的数据处理。

Shift Register with Parallel Load

并行加载的移位寄存器

该类型的移位寄存器可以根据加载信号（Load）的值，在并行加载模式和移位模式之间切换：

• 当 Load = 1 时：寄存器作为一个普通的 N 位寄存器工作，允许同时加载多个位的值。
• 当 Load = 0 时：寄存器作为一个移位寄存器工作，可以逐位地从串行输入中接收数据，并将数据移出。

这意味着该寄存器不仅可以用作串行到并行转换器（从 \( S_{in} \) 到 \( Q_{0:N-1} \)），还可以用作并行到串行转换器（从 \( D_{0:N-1} \) 到 \( S_{out} \)）。

移位寄存器的符号与实现

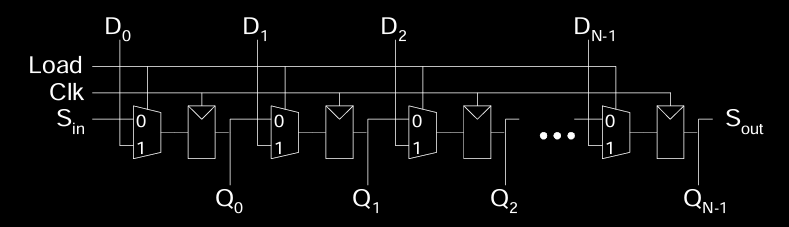
• 符号表示：在图示中，移位寄存器的每个位置（D0, D1, …, D_N-1）都表示一个单独的存储位，随着时钟信号的到来，寄存器可以在串行或并行模式之间切换。
  • Load 信号控制并行加载模式还是移位模式。
  • 在并行加载模式下，多个位的数据同时加载。
  • 在移位模式下，数据逐位从 \( S_{in} \) 输入并移出到 \( S_{out} \)。

Shift Register SystemVerilog Idiom

SystemVerilog 实现的移位寄存器

以下是用 SystemVerilog 实现的一个 8 位可配置的移位寄存器模块。通过这个模块，我们可以实现串行和并行加载两种功能。

module shiftreg #(parameter N=8)  // 参数化的移位寄存器，N 是寄存器位数
   (input logic clk,              // 时钟信号
    input logic reset, load,      // 重置信号和加载信号
    input logic sin,              // 串行输入信号
    input logic [N-1:0] d,        // 并行输入信号
    output logic [N-1:0] q,       // 并行输出信号
    output logic sout);           // 串行输出信号

   always_ff @(posedge clk, posedge reset) begin
     if (reset)                   // 当重置信号为高电平时，寄存器复位
       q <= 0;
     else if (load)               // 当加载信号为高电平时，进行并行加载
       q <= d;
     else                         // 否则进行串行移位操作
       q <= {q[N-2:0], sin};
   end

   assign sout = q[N-1];          // 串行输出信号取寄存器的最高位
endmodule

工作原理

• reset：当复位信号为高电平时，寄存器的所有输出 q 复位为 0。
• load：当加载信号为高电平时，输入的并行数据 d 同时加载到寄存器中。
• sin：当加载信号为低电平时，寄存器开始移位，将输入 sin 的值移入寄存器最低位，寄存器内的值向高位移一位。
• sout：寄存器最高位的值作为串行输出 sout。

这种灵活的设计让移位寄存器能够在并行和串行模式之间自由切换，适用于多种数据转换应用。

Verilog 实现的 8 位可配置移位寄存器

module shiftreg #(parameter N=8)  // 参数化的移位寄存器，N 是寄存器位数
   (input clk,                    // 时钟信号
    input reset, load,            // 重置信号和加载信号
    input sin,                    // 串行输入信号
    input [N-1:0] d,              // 并行输入信号
    output reg [N-1:0] q,         // 并行输出信号
    output reg sout);             // 串行输出信号

   always @(posedge clk or posedge reset) begin
     if (reset)                   // 当重置信号为高电平时，寄存器复位
       q <= 0;
     else if (load)               // 当加载信号为高电平时，进行并行加载
       q <= d;
     else                         // 否则进行串行移位操作
       q <= {q[N-2:0], sin};      // 移位操作：将串行输入 `sin` 移入最低位
   end

   always @(q) begin
     sout = q[N-1];               // 串行输出信号取寄存器的最高位
   end

endmodule

Memory

Memory Arrays

存储器阵列是用于高效存储大量数据的一种结构，能够通过唯一的地址来读取或写入对应的数据位。

• M 位的数据值通过每个唯一的 N 位地址进行读取或写入。
• 典型的存储器类型包括：
  • 动态随机存储器（DRAM）：需要定期刷新数据。
  • 静态随机存储器（SRAM）：无需刷新数据，速度快，但功耗相对较高。
  • 只读存储器（ROM）：存储的数据只能读取，不能修改。

结构

在存储器阵列中，地址通过 N 位地址线输入，从而选择对应的数据位。输出的 M 位数据表示当前所选单元存储的数据。

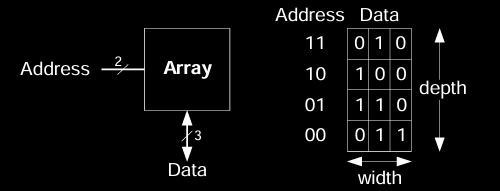
Memory Arrays Explained

存储器阵列可以看作一个二维的位单元阵列，每个位单元存储一个位的数据。N 位地址和 M 位数据的关系如下：

• 地址位数 N：决定行数，定义了存储阵列的深度（行数或单词数）。
• 数据位数 M：决定每个单词的位数，定义了存储阵列的宽度（每个单词的大小）。

深度（Depth）

深度表示行数，或者是存储器阵列中的单词总数。深度的大小等于 \(2^N\) 行。

宽度（Width）

宽度表示每行的列数，即每个单词的大小（以位为单位）。宽度等于 M 列。

阵列大小（Array Size）

存储器阵列的整体大小等于： \[ \text{大小} = \text{深度} \times \text{宽度} = 2^N \times M \]

例如，在一个二维的位单元阵列中，如果 N = 2 和 M = 3，存储器阵列有 \(2^2 = 4\) 行和 3 列，即有 4 个 3 位的单词。

Memory Arrays

在存储器阵列中，数据的存储和访问通过位于二维网格中的位单元进行。每个存储器单元可以存储一个位的数据，通常通过行和列（wordline 和 bitline）来访问。

1024-word x 32-bit Array

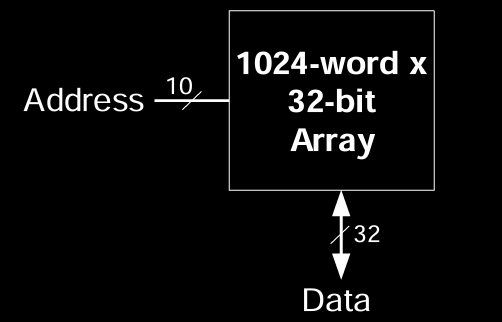
图示的是一个1024词 × 32位的存储阵列，其中：

• 地址位数为10：这意味着最多可以寻址 \(2^{10} = 1024\) 行，每行对应一个 32 位的数据字。
• 32 位数据：每个存储地址包含32位的宽度，即一个完整的数据单元。

Memory Array Bit Cells

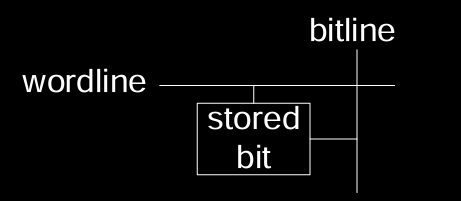
存储器的基本构建块是位单元（bit cell）。每个位单元包含以下关键部分：

• Wordline（字线）：决定是否对某一行的单元进行访问。
• Bitline（位线）：用于传输数据位的值，读出或写入单元。

操作逻辑：

• Wordline = 1 时激活该行，允许数据通过 bitline 读出或写入存储的值。
• Wordline = 0 时未激活该行，存储的数据保持不变。
  • 例如，如果位线处于高电平（1），则存储器单元保存 1；如果位线处于低电平（0），则保存 0。

Memory Array Wordline

Wordline（字线） 是存储阵列中控制一行访问的信号线：

• 它类似于使能信号（enable），用于选择某一行进行读写操作。
• 对于每个唯一的地址，只会有一条 wordline 处于高电平，意味着只有对应行被激活。

Wordline Operation

1. 地址解码器（decoder）将输入地址信号解码为对应行的 wordline 信号。
2. 在任一时刻，只有一行的 wordline 处于高电平，表明该行的数据可以通过位线读取或写入。

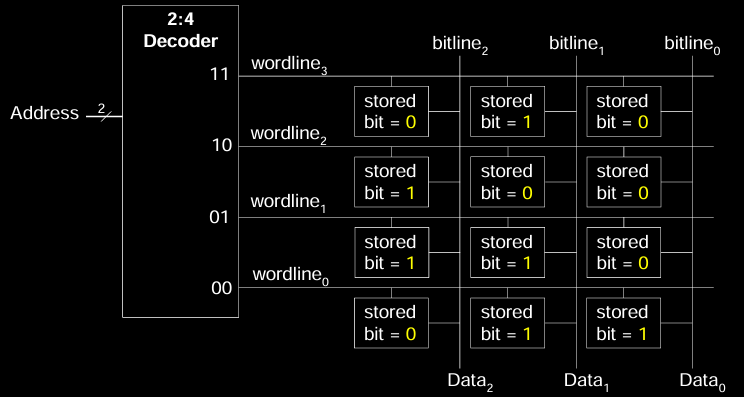
图示显示了一个二维存储阵列的示例，2:4 解码器用于选择 4 行中的一行（wordline0 到 wordline3），而每行对应不同的位线和数据存储单元。

Types of Memory

在数字设计和计算机架构中，存储器可以分为两大类：随机存取存储器（RAM）和只读存储器（ROM）。这两种存储器在数据保留、存取速度和用途上有显著差异。

RAM: Random Access Memory

RAM（随机存取存储器）是一种易失性存储器，这意味着当电源断开时，存储器中的数据会丢失。RAM 具有以下特点：

• 快速读写：数据可以快速存取，因此常用作计算机的主存储器。
• 广泛应用：现代计算机中使用的主要是 动态随机存取存储器（DRAM），它的特点是数据需要不断刷新，以防数据丢失。

随机存取意味着，存储器中的任意数据可以在等效时间内进行读取或写入，而不依赖数据的物理位置，这与顺序存取存储器（如磁带）不同。

ROM: Read Only Memory

ROM（只读存储器）是一种非易失性存储器，意味着即使在断电后数据仍会保留。ROM 具有以下特点：

• 只读：数据读取速度快，但写入通常不可行或非常缓慢。
• 应用广泛：例如，闪存常用于相机、U盘等设备中，且大多数的现代 ROM 可以通过特定方法进行有限的写操作（如烧录或编程）。

ROM 曾经仅能在制造时写入或通过熔断烧录，但随着技术发展，现代的闪存等类型的 ROM 提供了更多灵活的写入能力。

总结

• RAM 是易失性的，断电后数据丢失，适合快速读写操作的主存储器。
• ROM 是非易失性的，适合需要长期保存数据的应用场景，如存储固件和系统程序。

RAM

在数字系统中，RAM（随机存取存储器）是用于快速读写数据的一种存储设备。RAM具有两种主要类型：动态随机存取存储器（DRAM） 和 静态随机存取存储器（SRAM），它们的区别在于存储数据的方式和电路结构。

Types of RAM

1. DRAM (Dynamic Random Access Memory)
   DRAM 使用电容器存储数据，因此称为“动态”，因为电容器的电荷会逐渐泄漏，存储的数据需要周期性地刷新。在读操作后，数据会被破坏，因此也需要重新写入。DRAM的特点是高密度且相对较慢，但因为其结构简单，常用于大容量存储设备。

2. SRAM (Static Random Access Memory)
   SRAM 使用交叉耦合反相器来存储数据，数据在通电的情况下能够保持不变，因此不需要像DRAM那样定期刷新。SRAM 的存取速度更快，但因为结构复杂，它的存储密度较低，因此常用于缓存等高速存储器。

Robert Dennard and DRAM

罗伯特·德纳德（Robert Dennard） 于1966年在IBM发明了DRAM。当时很多人对这个概念持怀疑态度，担心其在实践中的可行性。然而，到1970年代中期，几乎所有计算机都开始使用DRAM作为其主要内存，确立了其在计算机内存中的重要地位。

DRAM 工作原理

DRAM 的数据位存储在电容器上，由于电容器中的电荷会随着时间的推移逐渐泄漏，因此称为动态存储器。为了保持数据，电容器需要定期刷新，即重复写入电荷。

• 刷新机制：电容器中的电荷会随着时间泄漏，若不及时刷新，数据会丢失。为了保持正确的值，内存控制器会在特定时间间隔对所有存储位进行重新写入。

• 读操作：由于读取操作会破坏电容中的电荷（即存储的数据），因此每次读取后必须进行重新写入。

下图展示了存储单元中如何通过电容器存储位，位线和字线则用于控制数据的写入和读取。

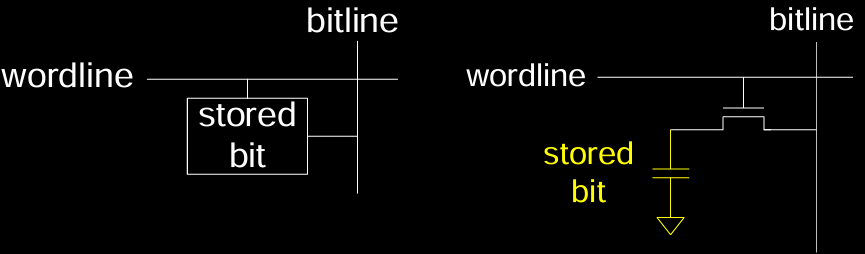
总结，DRAM 是现代计算机系统中广泛使用的主存储器，因为它在存储密度和成本方面具有优势。而SRAM则常用于高速缓存等场景，因其速度更快但成本较高。

DRAM (动态随机存取存储器)

DRAM 依赖于电容器来存储数据位，每个存储单元由一个电容和一个访问晶体管组成。当电容充满电时，表示存储的位为 1；当电容放电时，表示存储的位为 0。由于电容器中的电荷会随时间逐渐泄漏，因此 DRAM 需要定期刷新，以确保数据不丢失。

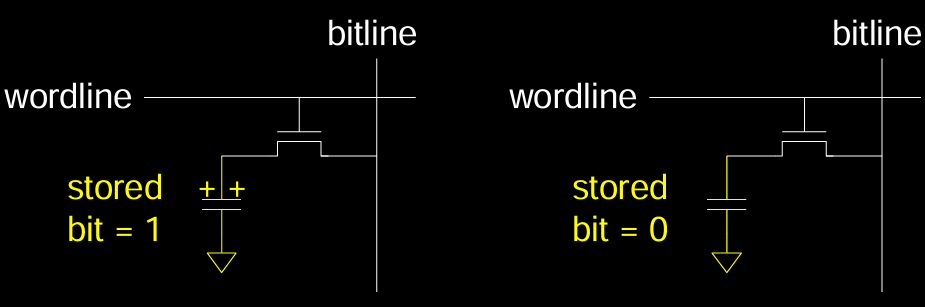
• 存储位为1：电容充满电，表示存储的位为1。电容器通过访问晶体管连接到位线，允许数据的读写操作。
• 存储位为0：电容放电，表示存储的位为0。即便电容器的电荷消失，也可以通过刷新来恢复数据。

DRAM 由于其高密度和低成本，被广泛应用于计算机主存储器中。

SRAM (静态随机存取存储器)

SRAM 使用交叉耦合反相器（即多个晶体管）来存储数据，每个存储单元由六个晶体管组成。与 DRAM 不同，SRAM 不依赖电容器，因此在通电时数据可以稳定保存，且不需要刷新。SRAM 的优点在于速度快且稳定，广泛应用于 CPU 缓存等高速存储场景。

• 存储位为1或0：SRAM 通过晶体管保持位的状态，数据可以通过位线快速读写。由于其结构复杂，SRAM 的存储密度较低，适合用于较小但速度要求较高的存储单元。

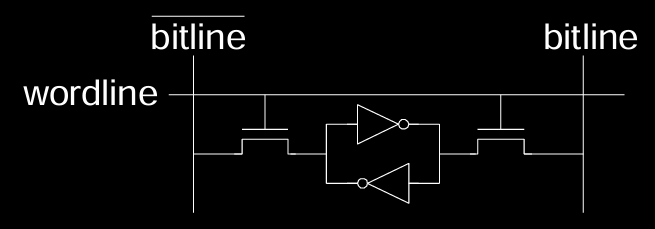
图中展示了 SRAM 的基本存储单元结构：

1. Wordline（字线）：每个存储单元通过一条字线连接，当选择访问某个存储单元时，字线会被激活（即信号被置高）。字线的作用是控制该存储单元是否参与读写操作。

2. Bitline（位线）：每个存储单元通过位线与外部读写电路相连。位线用于传输读出的数据或写入的数据。当进行写操作时，数据通过位线写入存储单元；进行读操作时，数据从存储单元通过位线传输出来。

3. 存储单元：
   • 存储一个比特：一个 SRAM 存储单元可以存储一个比特（0 或 1）。每个比特的存储是通过一个锁存器（latch）或者交叉耦合的反相器（inverter）来实现的。
   • 反相器对：图下方展示了一个典型的 SRAM 存储单元，使用了两个互相连接的反相器（inverter）构成一个反馈环路来存储比特数据。反相器会保持当前状态，直到外部干预为止，因此能在长时间内稳定地保存数据。
4. 访问晶体管：每个存储单元配备两个访问晶体管，它们充当开关，用于控制字线和位线的连接。只有当字线被激活时，这些晶体管才会导通，允许数据在位线和存储单元之间传输。每个晶体管与一个反相器的输出相连，用于从存储单元读取数据或向其写入数据。

SRAM 工作原理

1. 写操作：

• 当执行写操作时，字线被激活（置高），位线上施加需要写入的数据信号（0 或 1）。
• 访问晶体管导通，允许数据通过位线写入存储单元。
• 写入的数据通过反相器对锁存，并保持该值，直到下次写操作或电源关闭。

2. 读操作：

• 读操作时，字线被激活，打开访问晶体管。
• 存储单元中的数据被传送到位线，并通过读取电路读取该数据。
• 反相器对的反馈环路确保存储单元中的值在读取过程中保持不变。

SRAM 的特点

1. 快速访问：由于不需要周期性刷新数据（像 DRAM 那样），SRAM 具有非常快的读写速度，常用于 CPU 缓存、寄存器文件等高速存储应用场景。

2. 电源依赖性：SRAM 是易失性存储器，当电源关闭时，存储的数据会丢失。

3. 较大的单元面积：由于每个存储单元需要6个晶体管（通常是2个反相器和2个访问晶体管），SRAM 单元的面积较大，密度相对较低，因此用于较小容量的高性能存储，如 L1/L2 缓存。

4. 低功耗：与 DRAM 相比，SRAM 不需要频繁的刷新操作，因此在静态时的功耗较低，但由于其结构复杂，在动态读写时功耗会有所上升。

Memory Arrays Review

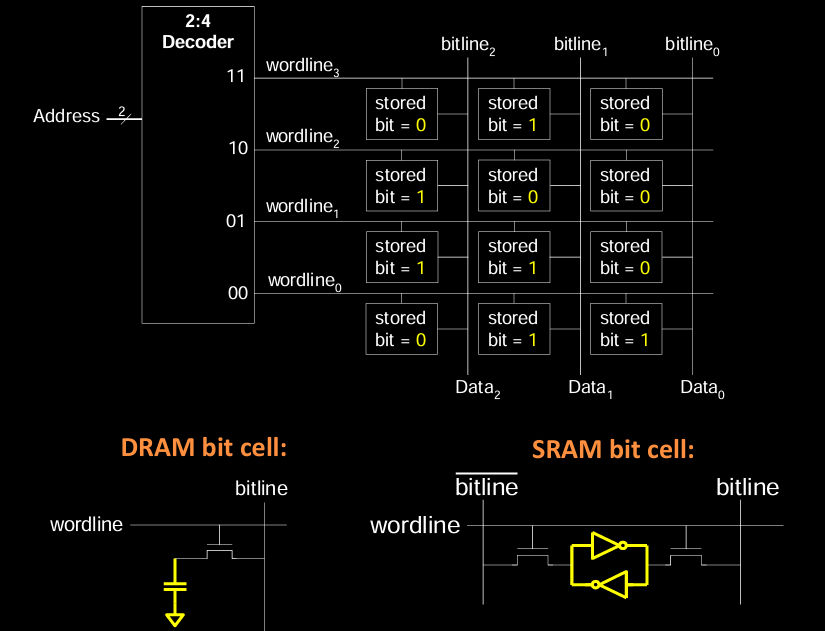
内存阵列通过二维的位元格组织存储数据，每行由地址解码器选择，列对应于位线，通过位线和字线的交互实现数据的读写。

• DRAM 单元阵列：每个单元由一个电容和一个晶体管组成，行地址通过字线选择，位线传输数据。在读取时，字线被激活，存储位的电荷通过晶体管传输到位线。

• SRAM 单元阵列：每个单元由交叉耦合反相器和访问晶体管组成。通过字线选择行，位线传递数据。SRAM 不需要刷新操作，能够更快地读写数据，但其成本更高，适合于较小的高速缓存等应用。

总结，DRAM 和 SRAM 各有优缺点。DRAM 具有高密度、低成本的优势，适用于大容量内存。而 SRAM 速度快，适用于需要快速响应的小型存储设备如缓存。两者结合使用，能够在不同层次的存储器中平衡性能和成本。

ROM

ROM（Read-Only Memory 只读存储器）是一种非易失性存储器，在设备断电后数据仍然能够保存。ROM 常用于存储固定程序或数据，例如嵌入式系统中的固件。ROM 的主要特点是数据只能读取，通常在制造时或通过特定编程方式写入一次。

ROM: Dot Notation

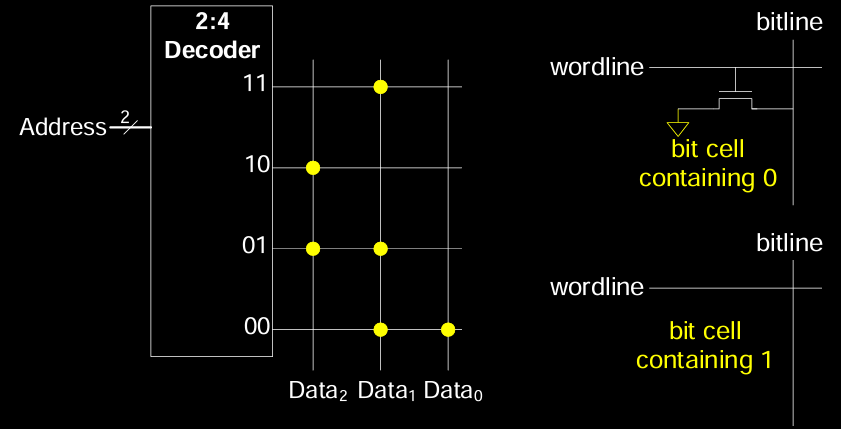
在 ROM 中，存储的数据通过”点阵”表示。通过地址解码器（例如 2:4 解码器），选择指定的字线（wordline），从而激活存储单元。每个存储单元通过位线（bitline）读取其中存储的位值。

• 位单元：ROM 中的位单元通常固定存储 0 或 1。使用”点”标记来表示存储单元中的值。
  • 存储0：使用某种电路设计来确保存储位为 0。
  • 存储1：通过不同的电路设计来固定存储位为 1。

ROM Storage

ROM 中的存储是一个二维数组，类似于内存阵列。在 ROM 中，行地址通过解码器选择，每行对应一个数据字（word），每个字包含若干位。

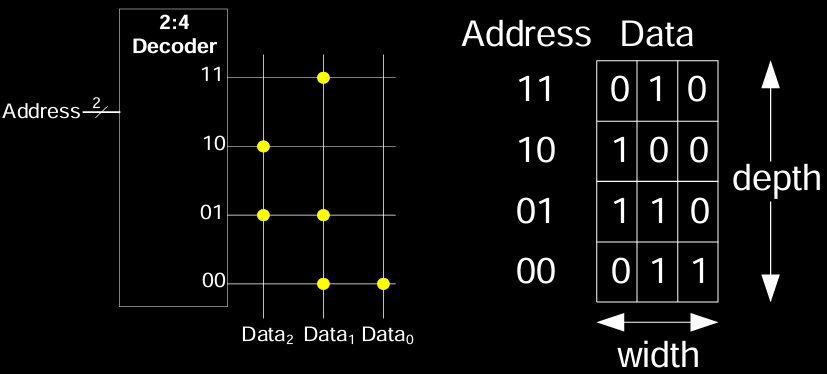
• 地址解码器：例如，一个 2 位地址（00、01、10、11）可以选择 4 行数据。
• 数据宽度：每行包含多个数据位。例如，3 位宽的数据意味着每行数据存储 3 位信息。

在 ROM 存储阵列的示例中，位线和字线通过硬件设计来确定每个存储单元的固定值。示例表明每个地址（从 00 到 11）可以对应不同的 3 位数据存储值，例如：

• 地址 00：数据为 011
• 地址 10：数据为 100

ROM 的存储设计允许在制造或特定编程时固定数据，并通过地址解码器读取。ROM 的结构简单且稳定，广泛用于那些需要长期保存数据的场景，但无法像 RAM 那样进行频繁的数据修改。

Fujio Masuoka, 1944-

藤尾正冈是一位日本工程师，在东芝（Toshiba）从1971年到1994年期间从事存储器和高速电路的开发工作。他最著名的贡献是发明了闪存（Flash Memory），这种发明最初是他在1970年代末未经授权的情况下利用夜晚和周末时间开发的。闪存的名称来源于他删除存储器数据时的现象，这让他联想到了照相机的闪光。

• 由于东芝对商业化进程缓慢，英特尔在1988年率先将闪存推向市场。
• 今天，闪存已经发展成一个每年价值250亿美元的市场，广泛应用于各类电子设备中，包括手机、数码相机和电脑。

ROM Logic (ROM 逻辑)

ROM（只读存储器）除了存储数据外，还可以用于实现逻辑函数。通过设计特定的位模式，ROM 可以作为固定逻辑电路。

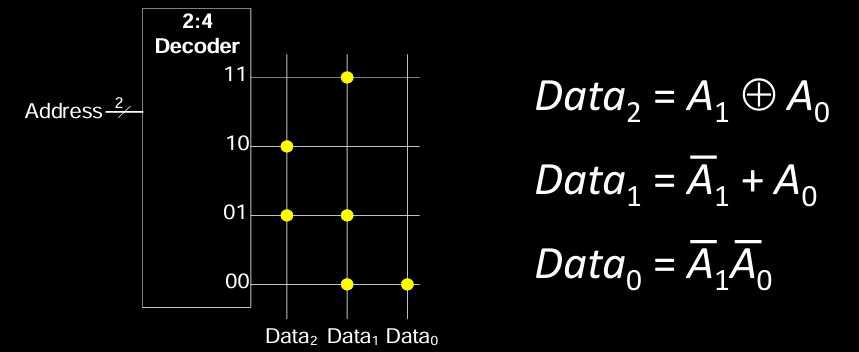
在这里的示例中，ROM 存储器实现了以下逻辑函数：

• Data₂ = A₁ ⊕ A₀（异或）
• Data₁ = A̅₁ + A₀（或门）
• Data₀ = A̅₁A̅₀（与非门）

ROM 的每个地址对应不同的输入组合，而存储的输出则代表逻辑函数的结果。在这个例子中，我们使用一个 2² × 3-bit ROM 来实现以下逻辑函数：

• X = AB （与门）
• Y = A + B （或门）
• Z = A̅B （与非门）

通过使用解码器（如 2:4 解码器），每个地址可以对应不同的输入 A 和 B 的组合（00, 01, 10, 11），并在 ROM 中存储相应的输出 X、Y 和 Z。这样，输入组合可以直接映射到输出逻辑，从而实现指定的逻辑功能。

这种方法广泛应用于逻辑电路设计中，尤其是用于实现复杂的组合逻辑。

Logic with Any Memory Array

使用任何存储器阵列（Memory Array）来实现逻辑功能是通过将输入地址解码并查找相应的存储数据来完成的。在这里，通过一个 2:4 解码器来解码输入地址，选择相应的字线（wordline），激活相应的存储单元，从而输出逻辑值。

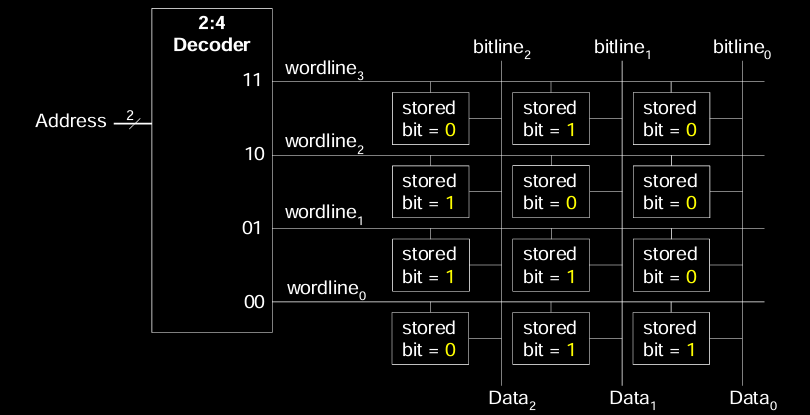
在图示中：

• Data₂、Data₁ 和 Data₀ 表示从存储器阵列中读取的三位数据，这些数据可用于实现特定的逻辑函数。每一行代表不同的地址（输入组合），而每一列则代表存储在该地址的输出数据。

Logic with Lookup Tables (LUTs)

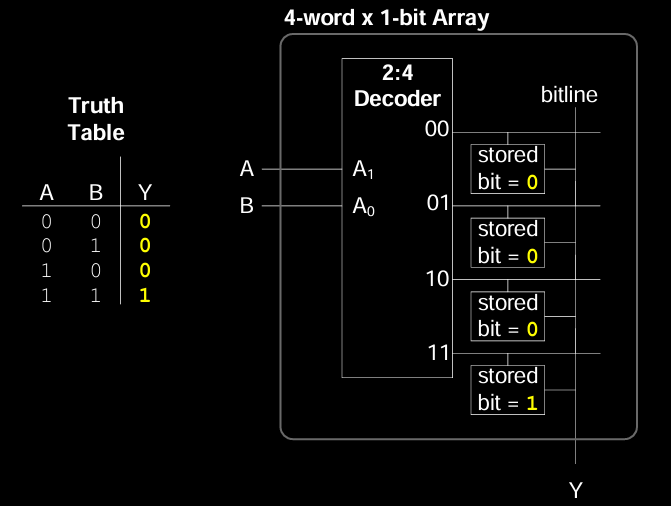
存储器阵列也可以作为查找表（LUT，Lookup Table）使用，即通过输入组合（地址）来查找对应的输出结果。在图示的例子中，真值表（Truth Table）展示了如何根据输入 A 和 B 的值来确定输出 Y。LUT 的原理与存储器阵列相似，输入作为地址，输出是预先存储的逻辑值。

举例说明：

• 当输入 A = 0，B = 0 时，输出 Y = 0。
• 当输入 A = 1，B = 1 时，输出 Y = 1。

LUTs 是现代数字电路设计中非常常用的一种方式，特别是在可编程逻辑器件（如 FPGA）中广泛应用，用于实现各种组合逻辑。

SystemVerilog & Multiported Memories

SystemVerilog和多端口存储器

SystemVerilog 提供了高效建模 RAM（随机存取存储器）和 ROM（只读存储器）的方式，能够支持不同的存储机制并通过多端口实现并行访问。

SystemVerilog RAM 代码示例

// 256 × 3 RAM with one read/write port
module ram (
    input  logic        clk,     // 时钟信号
    input  logic        we,      // 写使能信号
    input  logic [7:0]  a,       // 地址信号 (8位, 因为 2^8 = 256)
    input  logic [2:0]  wd,      // 写入数据 (3位)
    output logic [2:0]  rd       // 读出数据 (3位)
);

    logic [2:0] RAM [255:0];     // 定义 256 行，每行 3 位的 RAM

    assign rd = RAM[a];          // 通过地址 a 读出数据

    always_ff @(posedge clk) begin
        if (we)                  // 如果写使能信号有效
            RAM[a] <= wd;        // 将写入数据 wd 存入地址 a 对应的 RAM
    end
endmodule

在这里，定义了一个 256 × 3 的 RAM 模块，并使用了一个读/写端口。具体实现细节如下：

• module ram：定义了一个名为 ram 的模块，它接受时钟（clk）、写使能（we）、地址（a）、写入数据（wd）和输出读数据（rd）作为输入和输出。
• 内部的 RAM 数组使用 logic [2:0] RAM [255:0] 表示每个地址保存 3-bit 数据，共有 256 个地址。
• assign rd = RAM[a]：将地址 a 对应的 RAM 内容分配给读数据输出 rd。
• always @(posedge clk)：在时钟上升沿，如果 we 使能信号为高，则将 wd 写入 RAM[a] 地址中。

SystemVerilog ROM 代码示例

// 128 × 32 ROM with one read port
// 内容从文件初始化
module rom (
    input  logic [6:0]   a,   // 地址信号 (7位, 因为 2^7 = 128)
    output logic [31:0]  rd   // 读出数据 (32位)
);

    logic [31:0] ROM [127:0];  // 定义 128 行，每行 32 位的 ROM

    // 初始化文件内容到 ROM
    initial begin
        $readmemh("memfile.dat", ROM);  // 从 memfile.dat 文件加载数据
    end

    assign rd = ROM[a];  // 通过地址 a 读出数据

endmodule

此 ROM 模块实现了一个 128 × 32 的 ROM 并通过文件进行内容初始化。

• module rom：定义了名为 rom 的模块，接受地址 a 作为输入，输出读取的 32-bit 数据 rd。
• logic [31:0] ROM [127:0]：定义了 128 行，每行 32-bit 的 ROM 数据。
• initial $readmemh("memfile.dat", ROM)：通过文件 memfile.dat 初始化 ROM 的内容。$readmemh 是 SystemVerilog 提供的系统任务，用于从文件中加载十六进制格式的数据。
• assign rd = ROM[a]：将地址 a 对应的 ROM 数据分配给输出端 rd。

SystemVerilog ROM memfile 示例

// memfile.dat 文件示例
// 每行表示 32 位的十六进制数据，总共可以有 128 行

01234567
89ABCDEF
FFFFFFFF
A5A5A5A5
...

该部分定义了 memfile.dat 文件的格式，用来初始化 ROM 内容。每一行是一个 32-bit 的十六进制数，总共可以包含多达 128 行。每一行数据可以表示一个 ROM 地址的存储值。

通过这种方式，你可以在仿真过程中提前加载 ROM 的数据，模拟初始化的存储情况。这种做法非常有用，尤其是在实现控制器、查找表（LUT）加载预先配置的常量、微指令或者其他固定数据等功能时。

Verilog 实现的 RAM（256 x 3）

// 256 x 3 RAM with one read/write port
module ram(
    input clk,              // 时钟信号
    input we,               // 写使能信号
    input [7:0] a,          // 地址信号
    input [2:0] wd,         // 数据输入信号
    output reg [2:0] rd     // 数据输出信号
);

  reg [2:0] RAM [255:0];     // 256 x 3 的内存单元

  assign rd = RAM[a];        // 读取操作

  always @(posedge clk) begin
    if (we)                  // 如果写使能信号有效，进行写操作
      RAM[a] <= wd;
  end
endmodule

• reg [2:0] RAM [255:0]; 定义了 256 个 3 位的存储单元。
• 通过 assign rd = RAM[a]; 实现异步读取操作。
• always @(posedge clk) 实现同步写入操作，只有当写使能信号 we 有效时才执行写入操作。

Verilog 实现的 ROM（128 x 32）

// 128 x 32 ROM with one read port
// 内容从文件中初始化
module rom(
    input [6:0] a,           // 地址信号
    output reg [31:0] rd     // 数据输出信号
);

  reg [31:0] ROM [127:0];    // 128 x 32 的内存单元

  // 初始化内容，从 memfile.dat 文件中读取数据
  initial begin
    $readmemh("memfile.dat", ROM);
  end

  always @(a) begin
    rd = ROM[a];             // 根据地址读取数据
  end
endmodule

• reg [31:0] ROM [127:0]; 定义了 128 个 32 位的存储单元。
• 使用 $readmemh("memfile.dat", ROM); 初始化 ROM 的内容，memfile.dat 是一个包含 32 位十六进制数据的文件。
• 通过 always @(a) 实现同步读取，地址变化时更新输出 rd。

Multi-ported Memories

多端口存储器

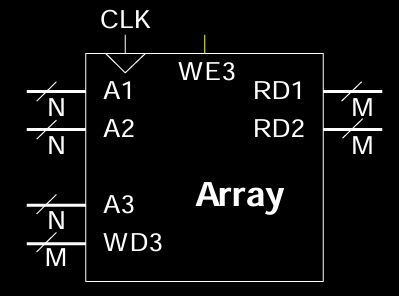
多端口存储器是具有多个读取和/或写入端口的存储器，可以同时支持多个数据访问操作。在图中展示的三端口存储器包括：

• 两个读取端口（A1/RD1, A2/RD2）
• 一个写入端口（A3/WD3, WE3：写入使能信号）

这种结构常用于寄存器文件中，寄存器文件是一个小型多端口存储器，用于存储处理器的寄存器数据。

SystemVerilog 多端口存储器代码示例

// 32 × 32 寄存器文件，带有2个读取端口和1个写入端口
// 寄存器0硬编码为始终读取0
module regfile(
    input  logic         clk,   // 时钟信号
    input  logic         we3,   // 写入使能信号
    input  logic  [4:0]  ra1,   // 读取地址1 (5位，因为 2^5 = 32)
    input  logic  [4:0]  ra2,   // 读取地址2 (5位)
    input  logic  [4:0]  wa3,   // 写入地址 (5位)
    input  logic [31:0]  wd3,   // 写入数据 (32位)
    output logic [31:0]  rd1,   // 读取数据1 (32位)
    output logic [31:0]  rd2    // 读取数据2 (32位)
);

    logic [31:0] rf [31:0];    // 32 × 32 位寄存器文件

    // 写入操作：在时钟上升沿，如果写入使能信号有效，则将 wd3 写入 wa3 地址对应的寄存器
    always_ff @(posedge clk) begin
        if (we3)
            rf[wa3] <= wd3;
    end

    // 读取操作：地址为0的寄存器始终返回0，否则返回对应地址的数据
    assign rd1 = (ra1 == 5'b00000) ? 32'b0 : rf[ra1];  // 寄存器0返回0
    assign rd2 = (ra2 == 5'b00000) ? 32'b0 : rf[ra2];

endmodule

代码说明

• 这个寄存器文件有两个读取端口（ra1/rd1 和 ra2/rd2）以及一个写入端口（wa3/wd3），支持同时读取和写入。
• rf 是一个 32 × 32 位的寄存器数组，用于存储 32 个 32 位寄存器的数据。
• 在时钟信号上升沿，若写入使能信号 we3 为高电平，写入数据 wd3 被存储到地址 wa3 指定的寄存器中。
• 读取端口会检查地址是否为 0，如果是，则返回 0；否则返回存储在对应寄存器中的数据。

这种多端口寄存器文件常用于处理器中，以支持快速的数据访问和并行的指令执行。

Logic Arrays: PLAs & FPGAs

逻辑阵列

逻辑阵列是可编程的硬件结构，允许用户通过配置不同的逻辑单元来实现所需的逻辑功能。

PLA（可编程逻辑阵列）

• 结构：由与阵列（AND array）和或阵列（OR array）组成。
• 功能：仅支持组合逻辑，不具备时序逻辑的能力。
• 内部连接：内部的逻辑连接是固定的，通过编程配置输入和输出的逻辑关系。
• 使用场景：适用于实现复杂的布尔逻辑表达式。

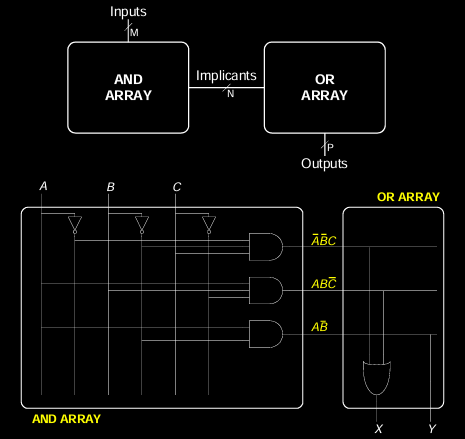
示例：

• X = \( \overline{A} \overline{B} C + A B \overline{C} \)
• Y = \( A \overline{B} \)

在图中，输入信号经过与阵列生成所有可能的与操作，然后将这些结果通过或阵列产生最终的输出。每个输出可以是多个与条件的或操作。

FPGA（现场可编程门阵列）

• 结构：包含一个逻辑单元（LE）数组，这些单元可以实现组合逻辑和时序逻辑。
• 功能：不仅支持组合逻辑，还支持时序逻辑（如寄存器），通过编程可以实现更加复杂的逻辑功能。
• 内部连接：连接是可编程的，用户可以通过配置内部连接来定义逻辑操作。

FPGA的灵活性更高，因为它可以通过重新编程来适应不同的应用，而PLA通常用于固定的逻辑实现。

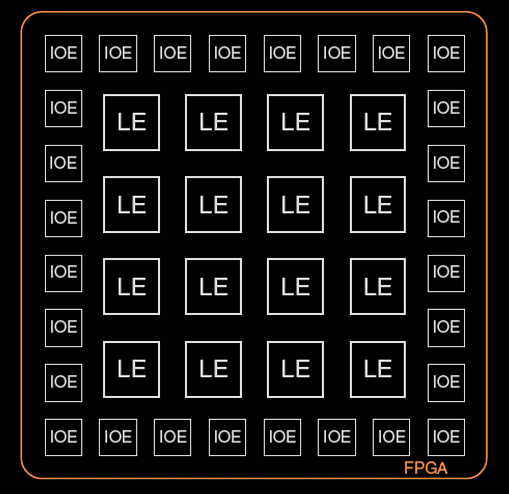
FPGA的核心特点是其灵活的结构，允许用户根据特定的逻辑需求进行编程和配置。它主要由以下几个部分组成：

• LEs（逻辑单元）：用于执行逻辑操作。LE是FPGA的基本计算单元，负责组合逻辑和时序逻辑的实现。
• IOEs（输入/输出单元）：用于与外部世界进行接口和通信。IOE控制输入输出信号与FPGA内部的传递。
• 可编程互连：连接逻辑单元和输入/输出单元，提供内部的可编程连接线路，使得逻辑单元能够按照需求连接在一起，形成完整的逻辑电路。

此外，某些FPGA还包含其他构建模块，如乘法器和RAM，以进一步增强其功能。

FPGA的总体布局

在FPGA的总体布局中，逻辑单元（LE）和输入/输出单元（IOE）是排列在一个二维阵列中的，如上图所示。通常，LE位于FPGA的中央区域，而IOE则位于周围，方便与外部设备的通信。可编程互连网络则贯穿整个芯片，将这些单元灵活连接起来。

LE（逻辑单元）

每个逻辑单元（LE）是FPGA的基本计算单元，主要由以下部分构成：

• LUT（查找表）：用于执行组合逻辑操作。查找表通过预定义的逻辑操作快速生成输出，类似于一个小型的存储单元，用于存储布尔逻辑的结果。
• 触发器（Flip-flop）：用于实现时序逻辑，能够存储和保持状态，支持时钟驱动的操作。
• 多路复用器（Multiplexer）：用于在LUT和触发器之间进行连接和切换，确保逻辑单元能够执行组合和时序逻辑的综合操作。

LE结合了组合逻辑和时序逻辑的功能，因此可以实现复杂的逻辑电路设计。LUT负责存储逻辑函数的结果，而触发器则保存时序状态，多路复用器确保这些单元之间的切换和连接，使得FPGA能够支持复杂的数字设计。

Altera Cyclone IV LE

Altera Cyclone IV LE 是一种逻辑单元，用于 FPGA 中实现复杂的逻辑功能。Cyclone IV LE 的设计充分体现了 LUT（查找表）和触发器的组合，允许实现组合逻辑和时序逻辑。

Altera Cyclone IV LE 结构

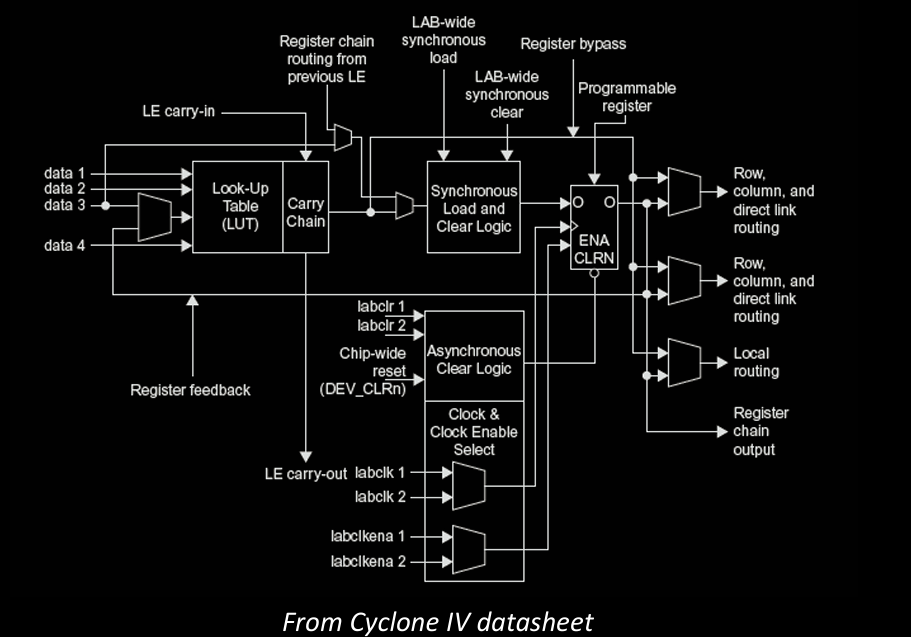
• 4输入LUT（Look-Up Table）：Cyclone IV LE 的 LUT 允许执行四个输入的逻辑运算。LUT 是 FPGA 逻辑单元的核心部分，它通过查找表将输入映射到输出，实现布尔逻辑。
• 寄存器输出（Registered Output）：LE 包含一个寄存器，可以用于存储时序逻辑的结果。寄存器用于时钟控制的逻辑，保证在时钟周期结束后状态保持。
• 组合逻辑输出（Combinational Output）：在不需要时序控制的情况下，LE 也可以通过组合逻辑直接输出结果。

LE 配置示例

LE 可以被配置成实现不同的逻辑功能。在这个示例中，配置 Cyclone IV LE 来实现以下两个逻辑功能：

• \( X = \overline{A} \overline{B} C + A B \overline{C} \)
• \( Y = A\overline{B} \)

配置步骤

1. X 的实现：
   • 使用 LUT 实现组合逻辑 \( \overline{A}BC + A\overline{B}C \)。LUT 可以存储所有可能输入组合对应的输出，形成一个逻辑电路。
2. Y 的实现：
   • 对于 \( A\overline{B} \) 这样的简单逻辑，可以直接通过 LUT 进行逻辑组合，实现输出。

通过这种方式，LUT 内存储了所有可能的输入组合的输出结果，寄存器用于需要时序逻辑的部分，最终输出通过组合或时序逻辑的组合来实现。这种灵活的结构使得 Cyclone IV LE 能够支持各种复杂的逻辑功能。

Logic Elements Example 1: 实现6输入的异或门（XOR）

为了实现逻辑表达式 \( Y = A_1 \oplus A_2 \oplus A_3 \oplus A_4 \oplus A_5 \oplus A_6 \)，我们可以通过使用Cyclone IV中的LUT进行分解。每个Cyclone IV的逻辑单元（LE）包含一个四输入的查找表（LUT），因此每个LUT最多可以处理四个输入。

解决方案

• 首先，将六个输入划分为两组：\( A_1 \oplus A_2 \oplus A_3 \oplus A_4 \) 和 \( A_5 \oplus A_6 \)。
• 使用一个LE来处理 \( A_1 \oplus A_2 \oplus A_3 \oplus A_4 \)。
• 使用另一个LE来处理 \( A_5 \oplus A_6 \)。
• 最后，使用第三个LE将前两个LE的输出进行异或操作。

因此，总共需要 3 个LE 来实现这个六输入异或门。

Logic Elements Example 2: 实现32位的2:1多路复用器

一个2:1多路复用器的基本功能是选择两个输入中的一个作为输出，这取决于控制信号。每个LE可以通过其LUT实现一个简单的2:1多路复用器。

解决方案

• 一个LE可以处理1位的2:1多路复用器。
• 对于32位的多路复用器，我们需要处理32个不同的位，每个位可以由一个独立的LE实现。

因此，总共需要 32个LE 来实现一个32位的2:1多路复用器。

Logic Elements Example 3: 实现任意有限状态机（FSM）

考虑一个任意的FSM，它有2位的状态、2个输入和3个输出。要实现这样的FSM，需要足够的LE来存储状态并实现状态转移逻辑。

解决方案

• 状态有2位，因此可以有最多 \( 2^2 = 4 \) 个不同的状态。
• 输入有2个，因此每个状态的转移逻辑将依赖于4个输入组合。
• 输出有3个，因此输出逻辑需要单独实现。

通常，FSM的实现涉及到状态存储和状态转移逻辑。LE将用于存储状态（需要至少2个LE）和实现状态转移和输出的逻辑。根据状态机的复杂性，实际使用的LE数量可能会有所变化，但估计需要 5到10个LE。

FPGA Design Flow

使用CAD工具（如Altera的Quartus II）设计FPGA的流程如下：

1. 设计输入：通过示意图输入设计，或使用硬件描述语言（HDL）编写代码。
2. 设计仿真：在设计完成后，仿真它以验证功能。
3. 综合设计并映射到FPGA：将设计综合并映射到FPGA的逻辑单元上。
4. 下载配置：将综合后的配置文件下载到FPGA中。
5. 测试设计：通过测试来确保设计按预期工作。