Lecture 3 Metrics & Verilog I

Review

在数字系统设计过程中，设计流程通常涉及多个层次的遍历。首先，必须从规格说明开始，然后进行建模、架构设计、RTL（寄存器传输级）设计，最后再到物理实现。这些步骤共同构建了数字系统的基础，而每一个步骤都至关重要，确保设计满足功能和性能要求。

同时，数字系统的核心是布尔逻辑，它依赖于一组布尔方程来实现运算。这意味着所有数字电路，无论是简单的逻辑门还是复杂的处理器架构，都是通过组合布尔代数的基础运算来实现其功能。这种层次化的方法使得复杂的设计可以通过模块化、系统化的方式逐步展开，实现从概念到物理实现的转变。

本节内容概要

Metrics

在设计过程中，我们评估一个系统的多个方面，这些评估指标（Metrics）包括：

功能性和鲁棒性（Functionality and Robustness）：这指的是系统能够正确地执行其指定功能，并在各种操作条件下稳定运行的能力。
成本（Cost）：成本通常分为开发成本和生产成本，设计决策需要考虑如何在保证功能性的同时，尽量降低成本。
性能（Performance）：衡量系统在特定应用场景下的响应速度和效率。
功耗与能效（Power and Energy）：这是衡量系统能耗的关键指标，尤其在现代移动设备和高性能计算中，能效显得尤为重要。

Verilog!

Verilog 是硬件描述语言（HDL）的一种，广泛用于数字电路的设计和模拟。它允许设计人员在抽象层次上描述硬件行为，从而将复杂电路简化为可理解的逻辑单元。Verilog 的主要特点包括：

概述（Overview）：Verilog 提供了对硬件设计的整体框架，从设计模块到信号流的细节都可以用 Verilog 描述。
组合逻辑（Combinational Logic）：在数字电路中，组合逻辑通过不依赖时钟信号的逻辑门直接实现输入到输出的映射，是 Verilog 描述中的一个重要部分。

Metrics

Design Tradeoffs

在设计过程中，通常需要在不同的性能、功耗和成本之间进行权衡。不同的设计需求和目标会导致选择不同的实现方案。例如：

低成本（Low Cost）：例如用于手表或计算器等设备，它们需要简单的功能和低制造成本。
低功耗（Low Power）：例如智能手机，这类设备要求较低的功耗以延长电池寿命，同时提供中等性能。
高性能（High Performance）：例如 Google 的 TPU（Tensor Processing Unit），它们专为高性能计算任务设计，能够处理大量并行计算，但功耗和成本较高。

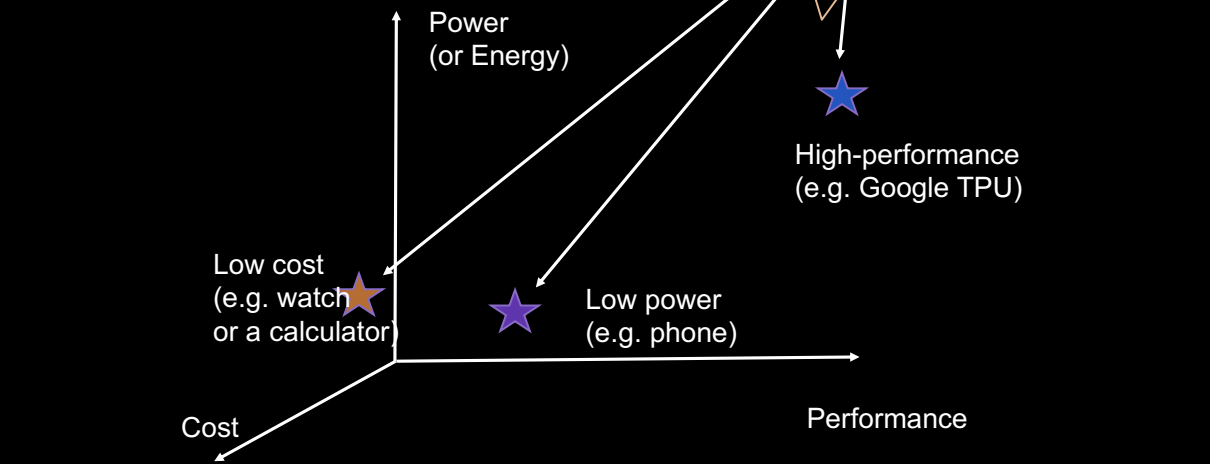
设计的目标功能通常位于这三者的平衡点上，设计人员需要根据应用场景的不同，选择最合适的设计方案，从而实现功能、性能和成本之间的最佳权衡。图中展示了三个设计目标之间的关系，突出显示了根据不同优先级所采取的设计策略：低成本、低功耗和高性能。

Beneath the Digital Abstraction

在数字系统的背后，逻辑门（Logic Gate）是通过将输入信号解释为0（低电平）和1（高电平）来执行其功能的。数字电路中，逻辑门使用二进制的0和1来代表不同的电压水平，通常0表示低电压，1表示高电压。具体来说，逻辑门的输入和输出是通过电压的变化来进行控制和表示的。

然而，数字电路并非完美无噪声。在实际的电路中，由于各种因素（如电流波动、环境干扰等），电压和电流都会出现不期望的变化，这种不规则的变化被称为噪声（Noise）。噪声会影响数字电路的稳定性，导致逻辑信号错误地被解释为高电平或低电平。

逻辑电平（Logic Levels）

逻辑电平是通过将连续的模拟电压映射为离散的二进制逻辑变量来定义的。常见的逻辑电平如下：

低电平（Low, 0）：对应的电压范围为[\(0, V_L\)]，其中 \(V_L\) 是表示逻辑0的名义电压（通常为0V）。
高电平（High, 1）：对应的电压范围为[\(V_H, V_{DD}\)]，其中 \(V_H\) 是表示逻辑1的最低有效电压，而 \(V_{DD}\) 是供电电压。

这种映射使得在数字系统中可以准确地区分0和1，尽管电路中的电压可能由于噪声而略有波动。

Noise Margins

噪声裕量（Noise Margins）是衡量逻辑门对噪声的敏感性的一种指标。它表示逻辑门在连接或级联时可以容忍的噪声大小。噪声裕量越大，意味着电路可以在更复杂或干扰更大的环境中工作，而不影响逻辑信号的正确解读。

噪声裕量的定义与逻辑电平密切相关，表示的是在最坏情况下输出信号仍然能够被正确解读为有效输入的噪声量。具体来说，噪声裕量分为两部分：

高电平噪声裕量（Noise Margin High, NMH）：当逻辑电平为高时，能承受的最大噪声电压。计算公式为： \[ NM_H = V_{OH} - V_{IH} \] 其中 \(V_{OH}\) 是逻辑1的输出电压，\(V_{IH}\) 是逻辑1的输入阈值电压。
低电平噪声裕量（Noise Margin Low, NML）：当逻辑电平为低时，能承受的最大噪声电压。计算公式为： \[ NM_L = V_{IL} - V_{OL} \] 其中 \(V_{OL}\) 是逻辑0的输出电压，\(V_{IL}\) 是逻辑0的输入阈值电压。

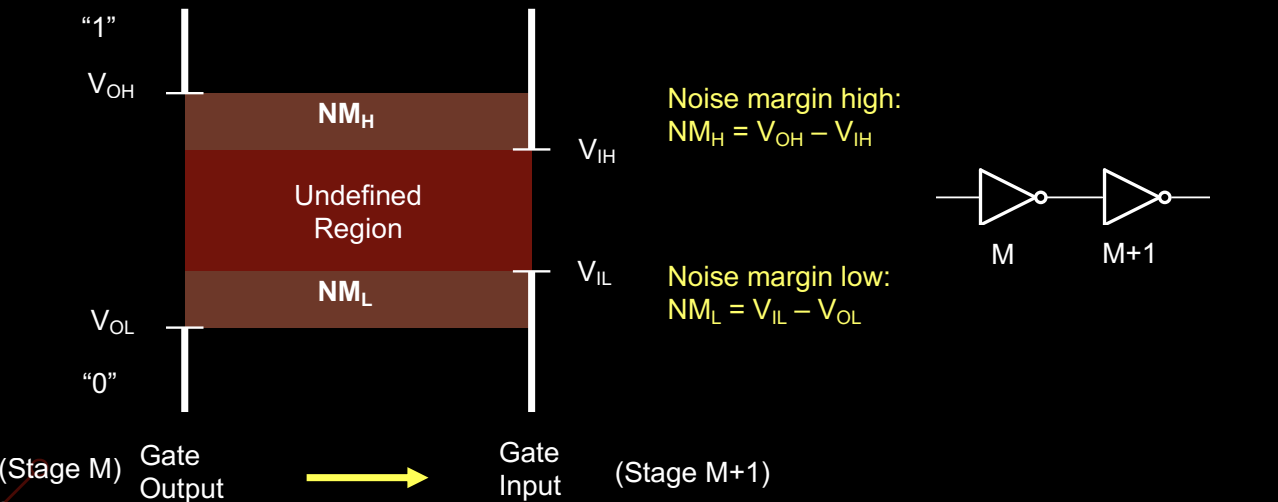
噪声裕量示意图

图中展示了一个逻辑门的输入输出电压的噪声裕量。输出电压可以是在低电平（VOL）或高电平（VOH）之间，而输入的阈值电压则界定了信号的有效性。当输入电压在 \(V_{IL}\) 和 \(V_{IH}\) 之间时，信号处于未定义区域（Undefined Region），此时可能会导致误判。在噪声裕量范围内，尽管信号受到干扰，电路仍然能够正确识别输入的逻辑状态。

通过级联逻辑门（如图中的 M 和 M+1），电路设计需要确保每一级逻辑门都能承受前一级的噪声影响，从而保持整个系统的稳定性和可靠性。

Voltage Transfer Characteristic

电压传输特性（Voltage Transfer Characteristic, VTC）描述了输出电压随输入电压变化的关系。在逻辑电路中，了解这一特性至关重要，因为它决定了逻辑门如何处理输入信号，并在噪声存在时保持稳定。

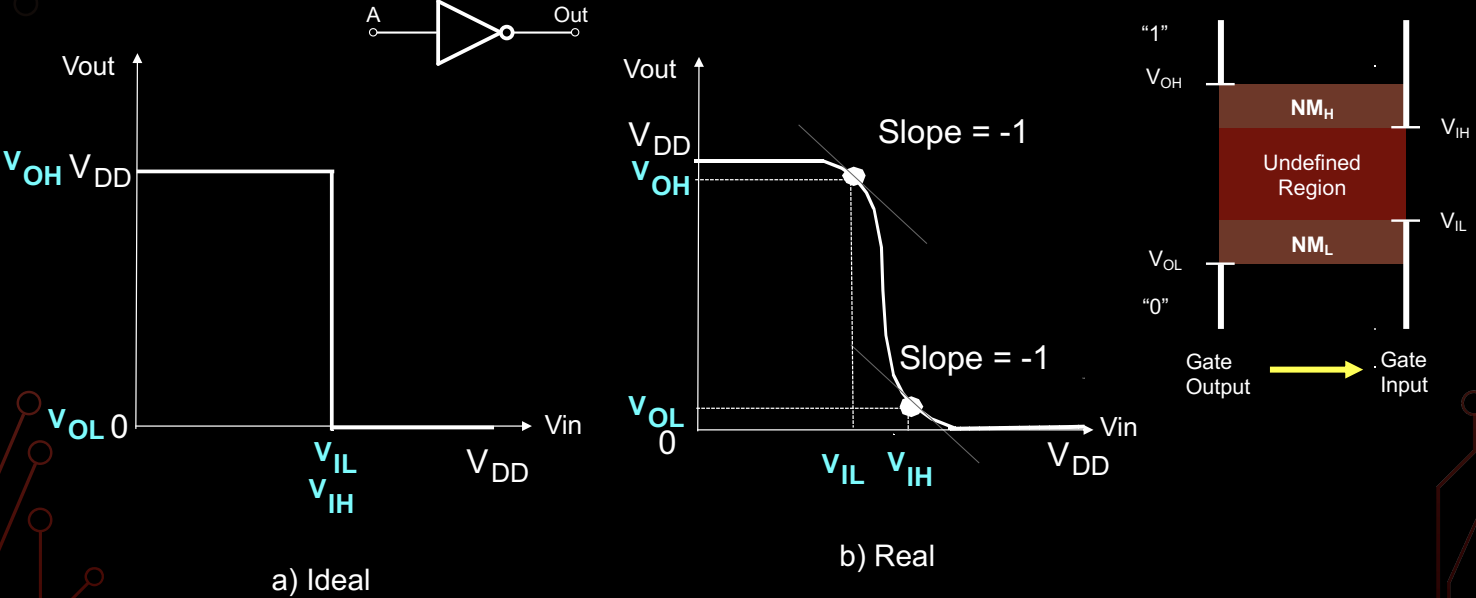
理想电压传输曲线

理想情况下，电压传输曲线呈阶梯状（如图 a 所示）。以非门为例，当输入电压 \(V_{in}\) 小于某一阈值 \(V_{IL}\) 时，输出电压保持在高电平 \(V_{OH}\)。当输入电压超过另一阈值 \(V_{IH}\) 时，输出电压转为低电平 \(V_{OL}\)。在理想情况下，这一切换过程是瞬时的，即曲线在阈值处是垂直的，保证了输入的微小变化不会导致输出电平的不确定性。

实际电压传输曲线

然而，在实际电路中，由于器件的非理想性，电压传输曲线并非完全垂直（如图 b 所示），而是具有一定的斜率。输入电压在 \(V_{IL}\) 和 \(V_{IH}\) 之间时，输出电压处于一个过渡区域，无法立即从高电平切换到低电平。这种过渡区域称为不确定区，电路在该区内的行为不如理想模型明确。

为了减小噪声对电路性能的影响，通常选择曲线斜率为-1的点作为关键设计点。这意味着当输入电压变化时，输出电压的变化速率恰好相等，能够最大限度地确保电路在输入信号变化时有明确的输出状态，从而提高噪声容限（noise margin）。

Regenerative Property

再生特性（Regenerative Property）是数字电路中一个重要的属性，保证了当信号受到干扰时，经过多级逻辑门之后，信号可以逐渐恢复到原本的名义电平。在实际电路中，信号会不可避免地受到噪声、干扰或其他因素的影响，导致电压偏离预期的逻辑电平。

再生门（Regenerative Gate）

再生特性确保当受扰动的信号通过多个再生门时，信号会逐步趋向稳定。例如，图中显示了输入信号 V0 受到扰动后，通过多级逻辑门（V1、V2、V3）逐渐恢复到稳定的逻辑电平。这种恢复是因为再生门的电压传输特性具有陡峭的过渡区，可以迅速将信号拉回到高电平或低电平，防止其落入未定义区域。

非再生门（Non-regenerative Gate）

相比之下，非再生门的电压传输特性不够陡峭，导致信号经过这些逻辑门时，不能有效恢复。这种门会使得信号的偏离更加严重，甚至可能最终导致逻辑错误。因此，在数字电路设计中，必须尽量使用再生门，以确保系统的鲁棒性和信号完整性。

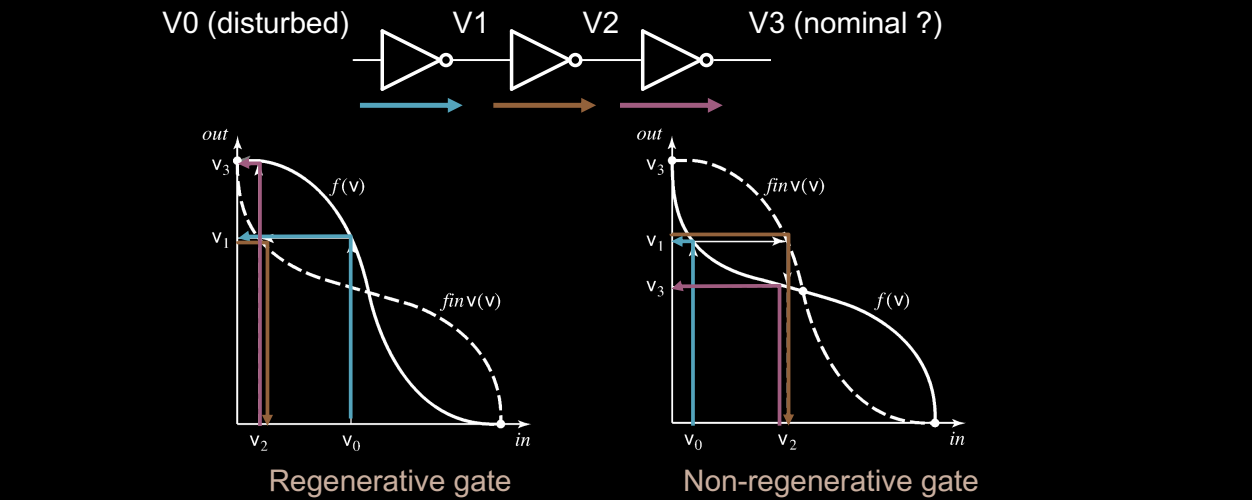
再生特性的关键

设计中，需要特别关注电压传输特性的过渡区域，确保逻辑门在这一区域具有明显的转换行为。一个清晰的过渡能够增强再生能力，帮助系统抵御噪声和扰动，从而确保信号在传输和处理过程中保持稳定。

通过引入再生特性，数字电路能够在面对输入信号波动时，依然保证输出信号的准确性。这在多个逻辑阶段（如处理器的多个级联电路）中尤为重要，确保了系统的整体稳定性和可靠性。

Cost

在硬件设计和制造中，成本分为一次性工程成本（Non-recurring Engineering, NRE Costs）和经常性成本（Recurring Costs）。这两种成本共同决定了集成电路（IC）的整体制造费用。

Non-recurring Engineering (NRE) Costs

NRE 成本是开发一款新的硬件时所需的固定、一次性成本。这个成本涵盖了从设计到验证所有相关的步骤，包括研究、设计和测试新硬件的支出。虽然这是一次性成本，但它会在整个产品生命周期内被分摊到每个出货的单位上。

例如，如果开发某硬件项目花费了 2000 万美元，并且计划生产 1 亿个单位，那么平均每个单位分摊的 NRE 成本为 0.20 美元。这种成本在批量生产时具有较强的规模效应——生产越多，每个单位分摊的 NRE 成本越低。

公式为： \[ \text{Cost per IC} = \frac{\text{Fixed Cost}}{\text{Volume}} + \text{Variable Cost per IC} \]

Recurring Costs

经常性成本是指制造、测试和封装每个单元的费用，这些成本在每次生产时都会发生。主要包括：

制造成本：制造芯片的基本成本，包括硅片（Wafer）的处理成本。
测试成本：每个芯片在出厂前的功能和性能测试费用。
封装成本：芯片最终的封装和保护费用。

以 16nm 制程为例，处理一个晶圆的成本大约是 1 万美元，每个晶圆可以产出不同数量的芯片，具体产量取决于芯片的大小。例如：

1 个 Cerebras 超大芯片
50-100 个大型 FPGA 或 GPU
200 个笔记本 CPU
超过 1000 个手机 SoC

经常性成本的公式为： \[ \text{Variable Cost} = \frac{\text{Cost of Die} + \text{Cost of Die Test} + \text{Cost of Packaging}}{\text{Final Test Yield}} \]

Die Yield

晶圆产率（Die Yield）是衡量晶圆生产中合格芯片数量的关键指标，直接影响生产成本。晶圆（Wafer）是由半导体材料制成的大块圆形硅片，经过处理后可以切割为多个独立的芯片（Die）。但是，并非每个晶片都能正常工作，因此需要考虑到生产过程中可能出现的缺陷，来计算有效的芯片数量。

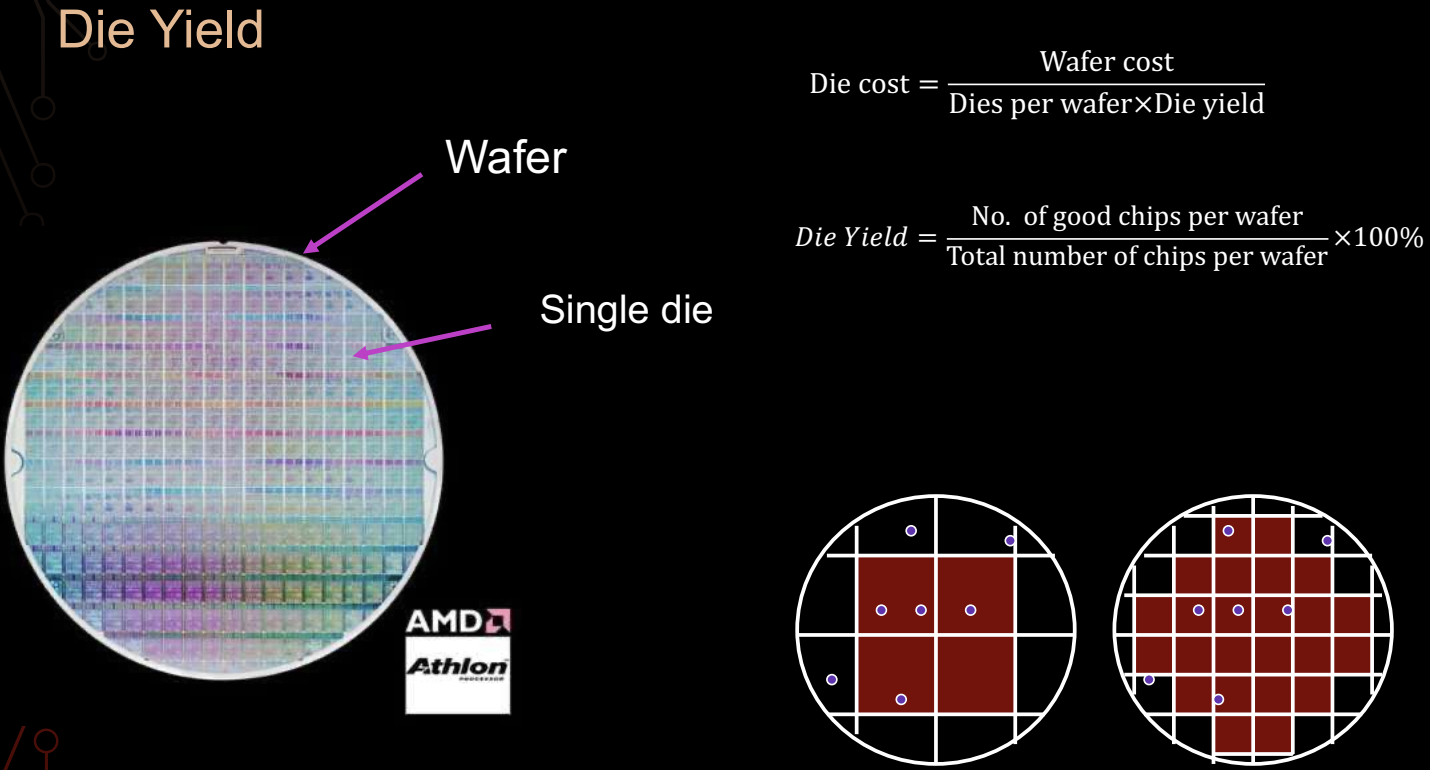
Die Yield 公式

晶圆产率的定义如下： \[ \text{Die Yield} = \frac{\text{No. of Good Chips per Wafer}}{\text{Total No. of Chips per Wafer}} \times 100\% \] 该公式描述了晶圆上能够生产出合格芯片的比例。例如，假设某个晶圆可以切割出 1000 个芯片，但由于缺陷只有 900 个是合格的，那么晶圆产率为 90%。

Die Cost 公式

晶片成本（Die Cost）则与晶圆成本和晶圆产率密切相关： \[ \text{Die Cost} = \frac{\text{Wafer Cost}}{\text{Dies per Wafer} \times \text{Die Yield}} \] 这个公式表明，晶片的生产成本不仅取决于晶圆的总成本，还取决于从每个晶圆上能够获得多少合格芯片。如果晶圆产率较低，意味着每个合格芯片的成本将大大增加。

通过提高产率或减少缺陷，制造商可以显著降低单位芯片的生产成本，进而提升整个生产线的经济性。

Defects

晶圆制造过程中的缺陷（Defects）是导致芯片产量（Yield）降低的主要原因。缺陷可能是由制造过程中材料、工具或环境的细微偏差引起的，导致部分芯片在功能上不合格。

芯片的尺寸对产率有着直接的影响。芯片面积越小，产率越高，这是因为较小的芯片受到缺陷（defects）的影响更小。我们可以结合这一点对芯片产率进一步说明：

在晶圆制造过程中，缺陷会随机分布在晶圆表面上。每个缺陷可能影响到一个或多个芯片的功能，导致这些芯片不合格。由于缺陷是随机的，如果芯片的面积较大，那么每个芯片被缺陷击中的概率就会增加，进而降低晶圆的总产率。

芯片面积对产率的影响：

大面积芯片：较大的芯片占据了晶圆更多的空间，因此更容易受到缺陷的影响。例如，如果一个缺陷出现在芯片中央，那么整个芯片可能无法使用。
小面积芯片：小芯片的面积相对较小，因此同样数量的缺陷只会影响较少的芯片。由于一个缺陷影响的面积较小，未被缺陷影响的区域仍然可以生成合格的芯片。因此，随着芯片面积的减小，产率提高，从而降低每个芯片的成本。

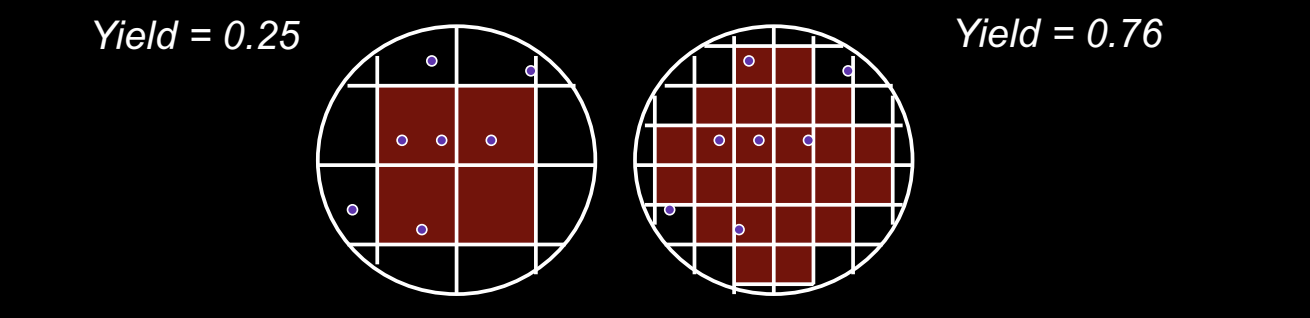
如图所示，左边的晶圆产率为 0.25，说明该晶圆上只有 25% 的芯片是可用的。而右边的晶圆产率为 0.76，意味着 76% 的芯片是合格的。产率越高，生产效率越高，每个芯片的平均成本也就越低。

Performance

Throughput

吞吐量（Throughput）衡量的是单位时间内执行的操作数量，通常以每秒操作次数（Operations per second）来表示。吞吐量是评估硬件性能的一个重要指标，尤其在高性能计算或实时应用中。

例如，Google 的 TPU v3 板卡能够执行 420 TFLOPS（每秒 10^12 次浮点运算），其中每次浮点运算采用 BFLOAT16 格式。这里需要注意，”操作”的定义可以是简单的 1-bit 加法（ADD）或更复杂的双精度浮点加法。因此，峰值吞吐量与平均吞吐量可能存在差异。

Latency

延迟（Latency）是指完成一个任务所需的总时间。例如，在手机上进行面部识别可能需要数十毫秒的时间来完成整个识别过程。延迟有时会用时钟周期来表示，可以包括平均延迟和尾部延迟（Tail Latency），其中尾部延迟是指最慢的一部分任务完成时间，通常用来评估最坏情况下的性能。

Digital Logic Delay

数字电路中，输入信号的变化不会立即反映在输出端。数字逻辑延迟（Digital Logic Delay）的原因在于每个逻辑门内存在有限的电阻和电容，导致信号传播需要一定的时间。

传播延迟（Propagation Delay）

逻辑门的传播延迟（tp）定义为输入变化后输出响应的速度，具体由输入信号和输出波形的 50% 转换点来计算。传播延迟可以分为两种：

高到低的转换（tpHL）：逻辑输出从高电平转换到低电平时的延迟。
低到高的转换（tpLH）：逻辑输出从低电平转换到高电平时的延迟。

传播延迟决定了电路的整体响应速度，对于高速运算或数据传输系统至关重要。

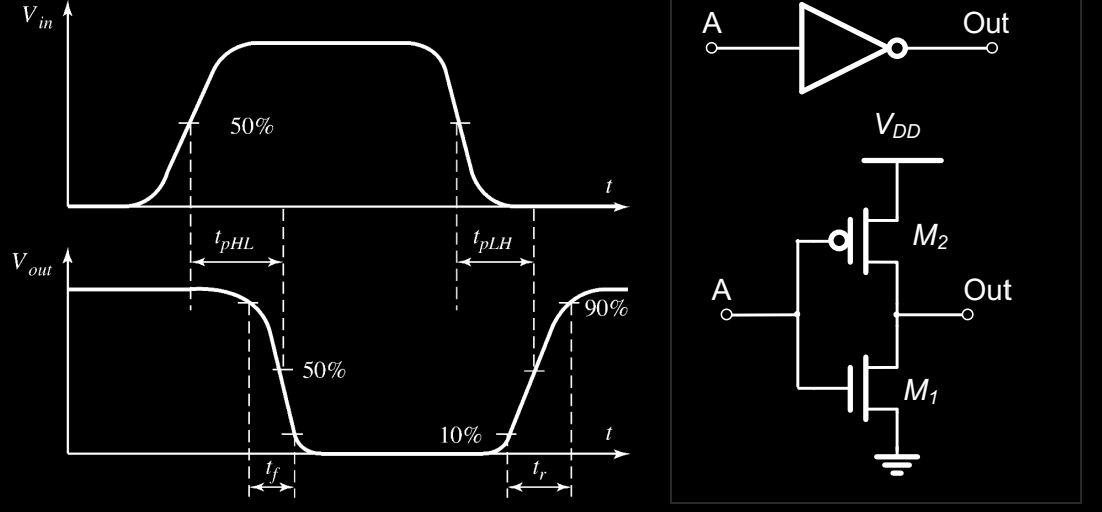
上升时间和下降时间（Rise and Fall Times）

除了传播延迟，信号的上升时间（tr）和下降时间（tf）也是衡量电路性能的关键指标。它们表示信号从 10% 转换到 90% 或从 90% 下降到 10% 的时间。这些指标决定了信号变化的锐度，对电路的高速操作和稳定性有直接影响。

信号上升时间和下降时间的快慢取决于电路的物理特性，例如电容和电阻。较快的上升和下降时间有助于提高电路的整体性能，但也可能导致信号完整性问题，因此需要在设计时进行权衡。

Digital Logic Timing

在数字电路中，数字逻辑时序（Digital Logic Timing）决定了系统的最大可实现时钟频率。系统中最慢的逻辑路径（即传播延迟最长的路径）通常限制了时钟频率的提升。在同步电路中，时钟信号用于控制逻辑块（CL blocks）和寄存器（Registers）之间的数据流动。

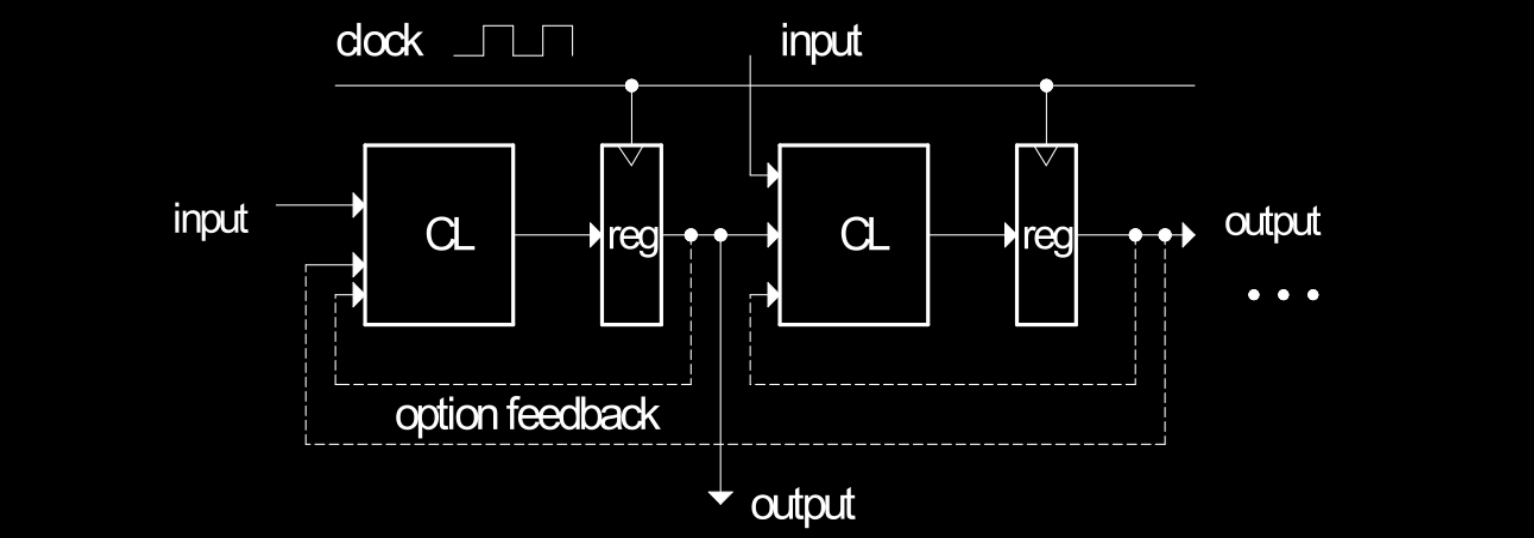
QQ_1725497355877

时钟频率与传播延迟

传播延迟是输入信号通过组合逻辑块（CL blocks）到达输出所需的时间。如果某个逻辑块的延迟过长，时钟周期必须延长以保证所有信号都能被正确处理。因此，整个系统的最大时钟频率由最慢路径的传播延迟决定。

要提高时钟频率，设计者需要识别出最长路径并采取优化措施使其运行更快。例如，重新设计逻辑以减少门的数量、提高元件的速度或减少寄生电阻和电容。

Energy and Power

在计算系统中，能量（Energy）和功率（Power）是两个重要的性能指标，尤其在移动设备和高性能计算中。

能量 (Joules, J)

能量是执行某项任务所需的工作量，例如对两个数进行加法运算或从内存中提取数据。能量的度量单位是焦耳（J）。系统处于激活或待机状态时都会消耗能量，不同的是激活状态下能量消耗显著较高。

例如，电池中的能量以焦耳或瓦特小时（Wh）存储，供系统执行任务时消耗。这也是电力公司根据千瓦时（kWh）收取费用的原因。

功率 (Watts, W)

功率是单位时间内消耗的能量，度量单位为瓦特（W），1 瓦特等于每秒消耗 1 焦耳能量（W = J/s）。功率可以是峰值功率，即系统短时间内的最高能耗，或是平均功率，即一段时间内的平均能耗。

功率决定了系统的散热需求。较高的功耗会增加散热器（Heat sink）、风扇或液冷系统的需求，以保证芯片在工作过程中不出现过热现象。散热设计的要求包括散热片的大小、热传导材料、空气流动方式（如强制空气冷却）以及是否使用液体冷却等。

Administrivia

Lab 1

Lab 1 应在本周完成：请独立完成第一个实验，并在需要时利用办公时间寻求帮助。

Lab 2

Lab 2 更为复杂：如果有条件，建议参加现场实验，能够更好地理解实验内容。

Homework 1

本周发布的家庭作业1：家庭作业将在本周发布，截止日期是下周五，建议尽早开始。

Discussion 1

讨论课 1：本周开始。建议与同学们互动，了解彼此，增强学习合作和交流的机会。

Verilog!

Hardware Description Languages

硬件描述语言（HDL）用于描述和模拟数字电路的结构与行为。它们允许设计人员通过代码描述硬件的功能，从而简化复杂系统的设计和验证过程。

Verilog

Verilog 语言的语法类似于 C 语言，适合描述硬件的结构和行为。
Verilog 已发展成熟，广泛应用于硬件综合和仿真，具备成熟的商用工具支持。
Verilog 是 UC Berkeley 的 EECS 151 和 251A 课程中的核心教学语言。

VHDL

VHDL 与 Verilog 语义上非常相似，但有更多的语法细节。
具备强大的类型系统，能在“综合时”（synthesis time）进行类型检查。
在某些政府项目和欧洲国家中仍广泛使用。

System Verilog

System Verilog 是 Verilog 的增强版，增加了强类型（Strong Typing）和其他改进特性，使其适合更复杂的硬件设计任务。

BlueSpec

BlueSpec 由麻省理工学院的 Arvind 教授发明，最初基于 Haskell 编程语言构建。
BlueSpec 目前已作为商用产品提供，网址为 bluespec.com。
见 lzzs.fun/MIT-digital-systems

Chisel

Chisel 是 UC Berkeley 开发的一种硬件描述语言，适用于高级硬件设计。
UC Berkeley 的 CS152 和 CS250 课程中使用 Chisel，相关资源可以在 chisel.eecs.berkeley.edu 找到。

Verilog: Brief History

Verilog 于 1985 年由 Automated Integrated Design Systems 公司（后改名为 Gateway）发明，后来在 1989 年被 Cadence 收购。
Verilog 最初被设计为一种仿真语言，最初并不注重硬件综合。但在 1980 年代，UC Berkeley 开发了许多用于综合的基础技术，这些技术在 1990 年代被商业化应用。
与 Verilog 同期，美国国防部开发了 VHDL（全称为 Very High-Speed Integrated Circuit Hardware Description Language），该语言公开可用，逐渐在政府和学术界流行起来。
为了应对 VHDL 的竞争，Cadence 于 1990 年将 Verilog 开源，允许公众使用，从而扩大其市场份额。

Verilog 最早因其与 C 语言的语法相似性及高质量的工具支持，成为硅谷公司设计硬件的首选语言，特别是用于商业芯片设计领域。

VHDL 在政府项目、欧洲、日本和一些大学中仍广泛使用。
目前，大多数主流的计算机辅助设计（CAD）框架都同时支持 Verilog 和 VHDL。

Verilog Introduction

在 Verilog 中，模块（Module）定义用于描述电路中的组件。模块是 Verilog 设计的基本构建块，通过定义模块的行为或结构，设计人员能够抽象出复杂的硬件系统。

描述模块内容的两种方式：

结构化 Verilog（Structural Verilog）：
- 使用子组件的列表及其连接方式，类似于用文本描述的原理图。
- 这种方法的代码编写繁琐，解读难度较大，但提供了对电路细节的精确控制。
- 结构化 Verilog 通常用于需要映射到 FPGA 或 ASIC 的特殊资源时。
行为化 Verilog（Behavioral Verilog）：
- 侧重于描述模块的行为，而不是具体如何实现。
- 行为描述可以被综合为符合该行为的电路，结果的质量取决于工具的性能。
- 该方法便于设计复杂系统，设计者无需关心电路的具体实现细节。

Verilog 允许构建模块的层次结构，顶层模块通常表示整个设计或用于测试设计的环境。通过模块化的方式，可以使复杂设计的管理和测试更加简单有效。

Logic Synthesis

逻辑综合（Logic Synthesis）是将 Verilog（或其他硬件描述语言 HDL）的高级描述转换为低级电路描述（网表 Netlist）的过程。Verilog 和 VHDL 最初都是仿真语言，但随着时间的推移，逐渐发展出自动化的综合工具，将 HDL 代码转换为可实现的硬件设计。

综合的原理

综合工具会将 Verilog 描述转化为基于特定技术的低级电路实现，例如：

FPGA：综合会使用查找表（LUT）、触发器（Flip-Flops）和块式 RAM（BRAM）等基本单元。
ASIC：综合会使用标准单元和内存宏单元。

这些技术特定的基本元件会被工具自动选取并连接，从而实现 Verilog 描述的硬件功能。

综合流程

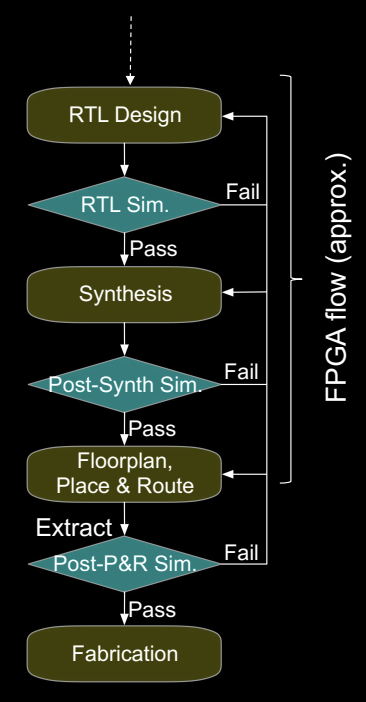
综合是硬件设计流程中的关键步骤，尤其在 FPGA 和 ASIC 流程中。典型的 FPGA 流程包括以下步骤：

RTL 设计：首先编写 RTL 代码，进行初步仿真（RTL Sim）。
综合（Synthesis）：RTL 代码经过综合工具转化为门级网表。
布线规划与路由（Place and Route）：在通过综合之后，工具会规划芯片上不同模块的布局，并连接它们。
提取与后仿真（Post-P&R Sim）：在实际布局与布线后，进行仿真验证，确保设计符合预期。
制造（Fabrication）：通过所有验证后，最终进入制造阶段。

该流程确保设计的正确性和可实现性，从仿真到硬件实现都保持一致性。

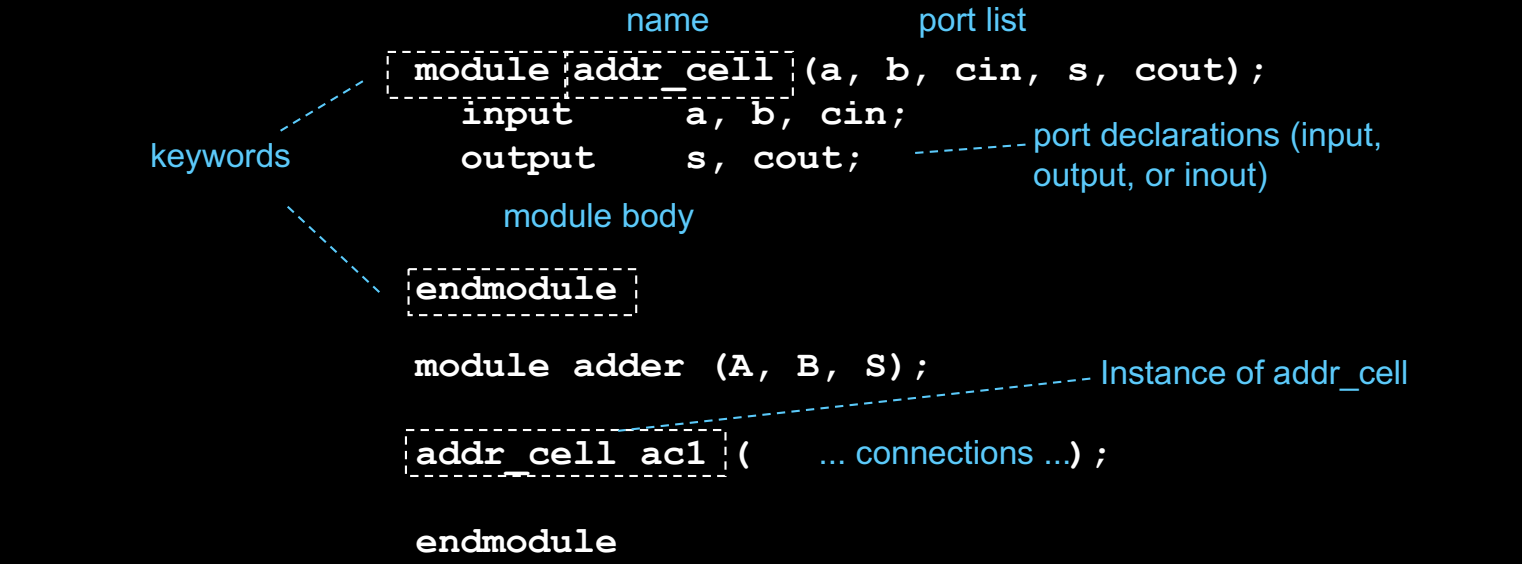
Verilog Modules and Instantiation

在数字电路芯片设计中，模块（Modules）用于定义电路组件。通过实例化（Instantiation），可以在设计中创建模块的层次结构。

模块名称（name）：模块的唯一标识符，用于表示不同的硬件功能块。
端口列表（port list）：模块的输入和输出端口，定义了数据流入和流出的路径。
端口声明（port declarations）：定义端口的类型，如 input、output 或 inout，表示数据是输入到模块、输出到外部，还是双向传输。
模块体（module body）：包含该模块内部的逻辑或其他子模块的实例化。
实例化（Instantiation）：在设计中引用子模块，创建模块的层次结构和不同功能单元的互连。
连接（connections）：将实例化模块的端口与外部信号或其他模块连接。

例子：加法器模块的实例化

module addr_cell(a, b, cin, s, cout);   // 这是一个全加器（full adder）的例子
    input a, b, cin;
    output s, cout;
endmodule

module adder(A, B, S);
    input [3:0] A, B;
    output [4:0] S;
    addr_cell ac1(.a(A[0]), .b(B[0]), .cin(0), .s(S[0]), .cout(C1));  // 实例化 addr_cell
    // 更多逻辑...
endmodule

模块的实例化将允许在更高级的设计中复用该模块。

Structural Model - XOR Example

在结构化建模中，电路是通过基本的逻辑门（如与门、或门、非门）来描述的。

内部信号声明（internal signal declarations）：定义模块内部用于连接不同逻辑门的信号（例如 wire 声明）。
内建门（built-in gates）：例如 not、and 和 or 等基本逻辑门，用于组合信号。
实例名称（instance name）：为每个逻辑门的实例分配一个唯一的标识符，方便在设计中引用。
互连（interconnections）：连接不同门的输入输出信号，定义信号流动的路径。

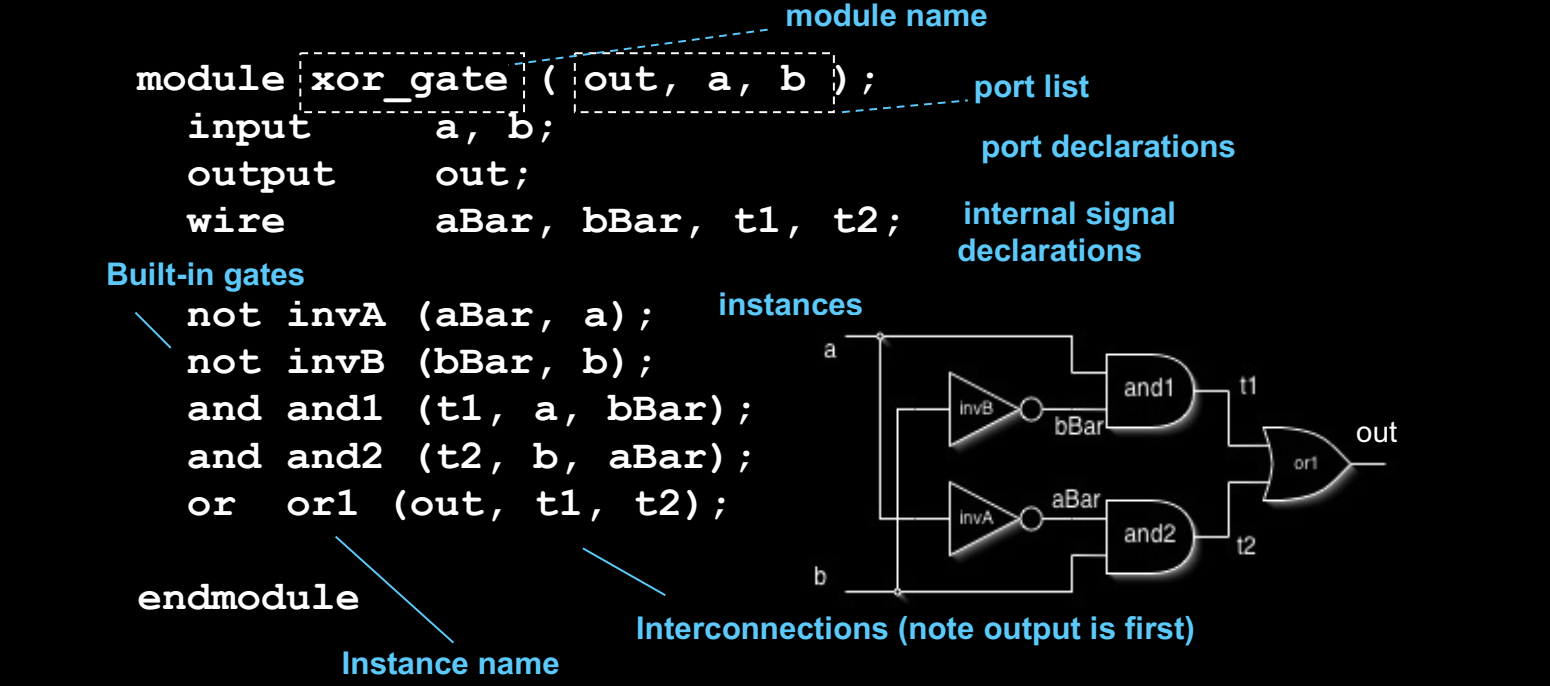
例子：使用基本逻辑门实现 XOR

module xor_gate(out, a, b);
    input a, b;
    output out;
    wire aBar, bBar, t1, t2;
  
    not invA(aBar, a);        // 取 a 的反
    not invB(bBar, b);        // 取 b 的反
    and and1(t1, a, bBar);    // a 和 b 的反与
    and and2(t2, b, aBar);    // b 和 a 的反与
    or or1(out, t1, t2);      // 或操作，产生 XOR 输出
endmodule

重要注意事项：

实例化的门不需要“执行”：逻辑门始终处于活动状态，实时响应输入信号的变化，而不需要显式调用。
门的复用性：Verilog 内置的逻辑门（如 xor）已经存在，通过基础门组合实现 XOR 的目的是展示底层逻辑。
信号声明问题：未声明的信号在 Verilog 中默认会被视为 wire 类型。确保所有信号正确声明，以避免潜在的设计错误。

通过这种结构化建模方式，可以明确地看到每个逻辑门之间的信号连接，逐步构建复杂的电路。

在数字电路芯片设计中，模块化设计 是一种核心方法，它将复杂电路分解为多个功能模块，以便于设计、验证和复用。通过模块化，设计者可以将不同的功能单元封装成独立的模块，然后通过实例化（Instantiation） 将它们组合起来，形成更复杂的系统架构。

模块（Modules）

Verilog 模块定义了电路的基本功能单元，每个模块具有独立的输入、输出端口，以及内部逻辑。模块可以是组合逻辑电路或时序电路，这取决于其内部实现。

模块名称（name）

每个模块有一个唯一的名称，用于标识和引用。例如，一个模块可以是一个全加器、计数器或寄存器。

端口列表（port list）

模块的端口定义了它与外部世界的交互。端口可以是输入、输出或双向端口，它们用于传递数据或控制信号。例如：

输入端口（input）：用于接收外部信号。

输出端口（output）：模块计算后的结果输出到外部。

双向端口（inout）：既可以作为输入，也可以作为输出（通常用于三态逻辑）。

端口声明（port declarations）

在模块的端口声明中，设计者需要指定每个端口的类型是 input、output 或 inout，并定义它们的位宽。例如：
input [3:0] A;    // 定义 4 位输入信号 A
output [4:0] S;   // 定义 5 位输出信号 S
模块体（module body）

模块体中包含了模块的内部逻辑，它可以由基本的逻辑门（如 and、or、not），或者其他子模块实例化而成。模块体的逻辑实现决定了模块的行为。

模块实例化（Instantiation）

实例化 是模块复用的重要机制，允许在顶层模块中引用子模块。通过实例化，可以将设计分解为多个子模块，并且在顶层进行组合和互联。这种方式不仅提高了设计的可读性和可维护性，还促进了设计的模块化和功能复用。

实例化子模块（Instantiating Submodules）

当需要在设计中使用一个已经定义好的模块时，可以通过实例化来调用它。例如：
addr_cell ac1(.a(A[0]), .b(B[0]), .cin(0), .s(S[0]), .cout(C1));
在这个例子中，addr_cell 模块被实例化为 ac1，并将端口 a、b、cin、s 和 cout 连接到外部信号。

命名端口（Named Ports）

为了使代码更易于阅读和理解，通常使用命名端口的方式进行模块实例化。命名端口明确了信号与端口的对应关系，避免了端口位置混淆。示例如下：
addr_cell ac1(
    .a(A[0]), 
    .b(B[0]), 
    .cin(0), 
    .s(S[0]), 
    .cout(C1)
);
这种命名方式使得设计者可以清晰地看到每个信号如何与模块端口连接。

模块实例化层次结构

通过模块实例化，可以建立一个多层次的设计结构。在顶层模块中，可以实例化多个子模块，然后通过信号将它们互连。例如，一个 4 位加法器可以由四个全加器组成，每个全加器处理一位的加法，进位传递到下一位：
module adder(A, B, S);
    input [3:0] A, B;
    output [4:0] S;
    wire C1, C2, C3;

    addr_cell ac0(.a(A[0]), .b(B[0]), .cin(1'b0), .s(S[0]), .cout(C1));
    addr_cell ac1(.a(A[1]), .b(B[1]), .cin(C1), .s(S[1]), .cout(C2));
    addr_cell ac2(.a(A[2]), .b(B[2]), .cin(C2), .s(S[2]), .cout(C3));
    addr_cell ac3(.a(A[3]), .b(B[3]), .cin(C3), .s(S[3]), .cout(S[4]));  // 最后的进位输出到 S[4]
endmodule
通过这种层次结构，设计人员可以轻松地构建复杂的电路系统。

内部信号声明（Internal Signal Declarations）

在设计复杂电路时，通常需要声明内部信号（wire）来连接不同的逻辑门。例如：
wire aBar, bBar, t1, t2;
这些 wire 信号用于存储和传递中间结果。

基本逻辑门的实例化（Built-in Gates）

Verilog 提供了一些内置的基本逻辑门，如 and、or、not 等，用于逐位操作信号。通过这些基本逻辑门，设计者可以构建复杂的组合逻辑电路。例如，在实现一个 XOR 门时：
not invA(aBar, a);       // 取 a 的反
not invB(bBar, b);       // 取 b 的反
and and1(t1, a, bBar);   // a 和 b 的反与
and and2(t2, b, aBar);   // b 和 a 的反与
or or1(out, t1, t2);     // 或操作，产生 XOR 输出
通过将这些基本门组合在一起，设计者可以实现复杂的逻辑功能，如异或（XOR）操作。

互连与信号流动（Interconnections and Signal Flow）

逻辑门之间的信号通过互连传递，定义了信号的流动方向。每个逻辑门的输出会作为其他逻辑门的输入，形成完整的电路。例如：
and and1(t1, a, bBar);   // t1 接收 a 和 b 的反的与运算结果
or or1(out, t1, t2);     // 最终将 t1 和 t2 的结果传递到输出

Instantiation, Signal Array, Named Ports

模块实例化（Instantiation）是 Verilog 中将一个模块作为子模块嵌入到另一个模块中的过程。通过实例化，可以构建复杂的电路层次结构。在这个例子中，我们展示了 4:1 多路复用器（MUX）的实例化，使用了信号数组和命名端口。

示例：4:1 MUX

module mux4 (in0, in1, in2, in3, select, out);
    input in0, in1, in2, in3;    // 4 个输入信号
    input [1:0] select;          // 2 位选择信号，信号数组
    output out;                  // 输出信号
    wire w0, w1;                 // 中间信号

    // 实例化两个 2:1 MUX
    mux2 m0 (.select(select[0]), .in0(in0), .in1(in1), .out(w0));
    mux2 m1 (.select(select[0]), .in0(in2), .in1(in3), .out(w1));
    
    // 最终选择的输出
    mux2 m3 (.select(select[1]), .in0(w0), .in1(w1), .out(out));
endmodule

说明：

信号数组：input [1:0] select; 声明了一个 2 位的选择信号数组，用于控制多路复用器的选择。
命名端口（Named Ports）：模块实例化时，使用 .端口名(信号) 的方式连接内部信号与模块的输入/输出端口。命名端口有助于提高代码的可读性，尤其是在端口较多的复杂模块中。

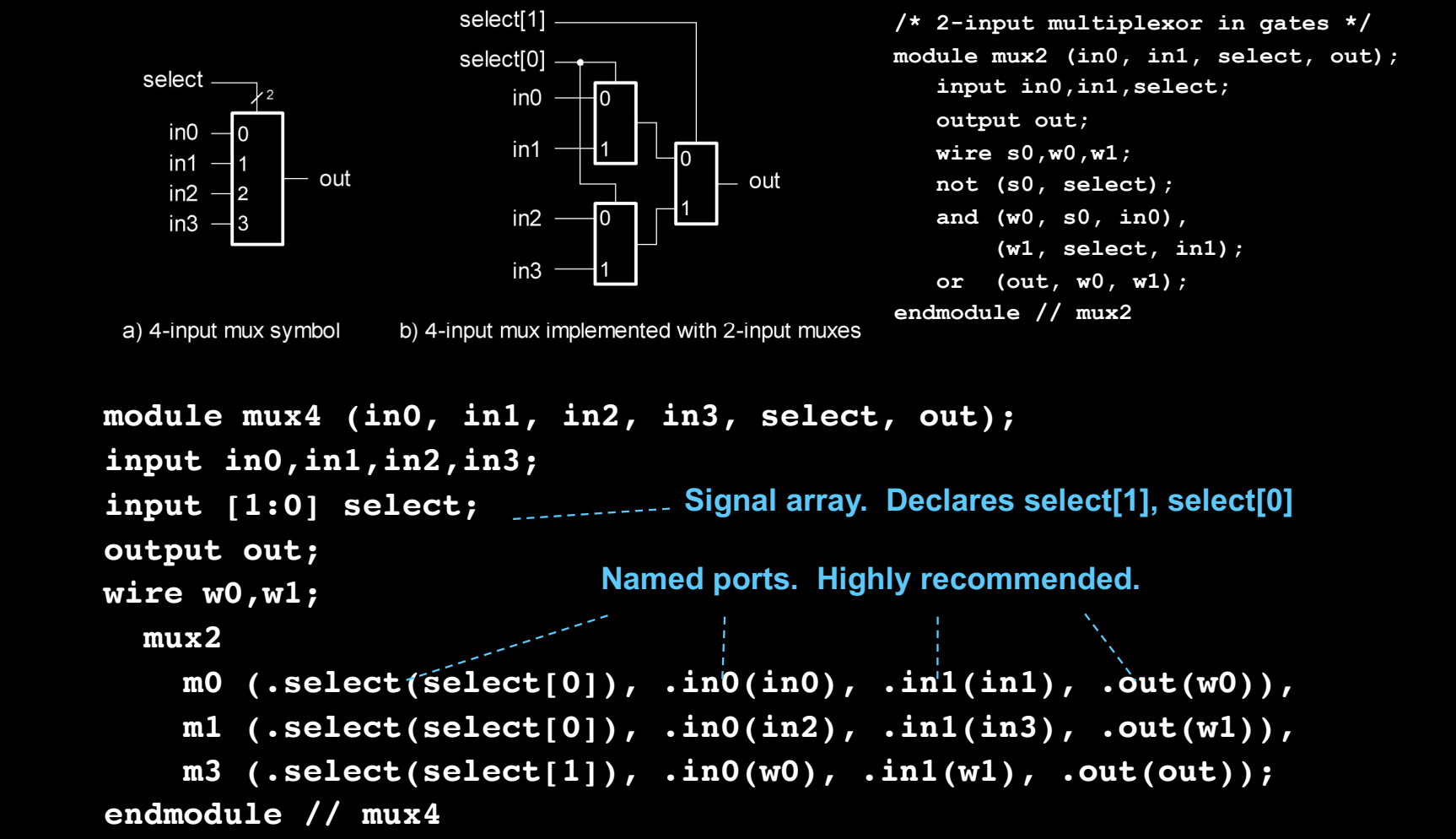
2:1 MUX 的实现

module mux2 (in0, in1, select, out);
    input in0, in1, select;   // 输入端口
    output out;               // 输出端口
    wire w0, w1;              // 中间信号

    // 逻辑实现
    not (w0, select);         // 取反 select
    and (w0, w0, in0);        // select 为 0 时，输出 in0
    and (w1, select, in1);    // select 为 1 时，输出 in1
    or  (out, w0, w1);        // 输出选择结果
endmodule

在 mux4 模块中，通过实例化多个 mux2 模块来实现 4:1 的多路复用功能。每个 mux2 实现 2:1 的选择，最后再根据 select[1] 来选择最终输出。

Simple Behavioral Model

行为建模（Behavioral Modeling）是一种使用 Verilog 中的连续赋值（continuous assignment）语句来描述逻辑功能的方式。这种建模方式注重描述模块的行为，而不是具体的电路实现。

示例：简单行为模型

module foo (out, in1, in2);
    input in1, in2;      // 输入信号
    output out;          // 输出信号

    // 连续赋值，表示 out = in1 & in2 的逻辑与操作
    assign out = in1 & in2;
endmodule

说明：

连续赋值（Continuous Assignment）：assign 语句用于描述逻辑关系，该语句表示右边的表达式会持续地赋值给左边的输出信号，任何输入变化都会立即反映在输出上。这不同于传统编程语言中的赋值，后者只有在执行到相应代码时才会更新。

在这个例子中，assign out = in1 & in2; 表示 out 始终是 in1 和 in2 之间按位与操作的结果，类似于手动实例化一个位与门（AND Gate）。

Example - Ripple Adder

波纹进位加法器由多个全加器（Full Adder, FA）级联而成，每个全加器处理一位的加法，并将进位传递给下一个全加器。下面是 Verilog 中实现 4 位波纹进位加法器的代码示例。

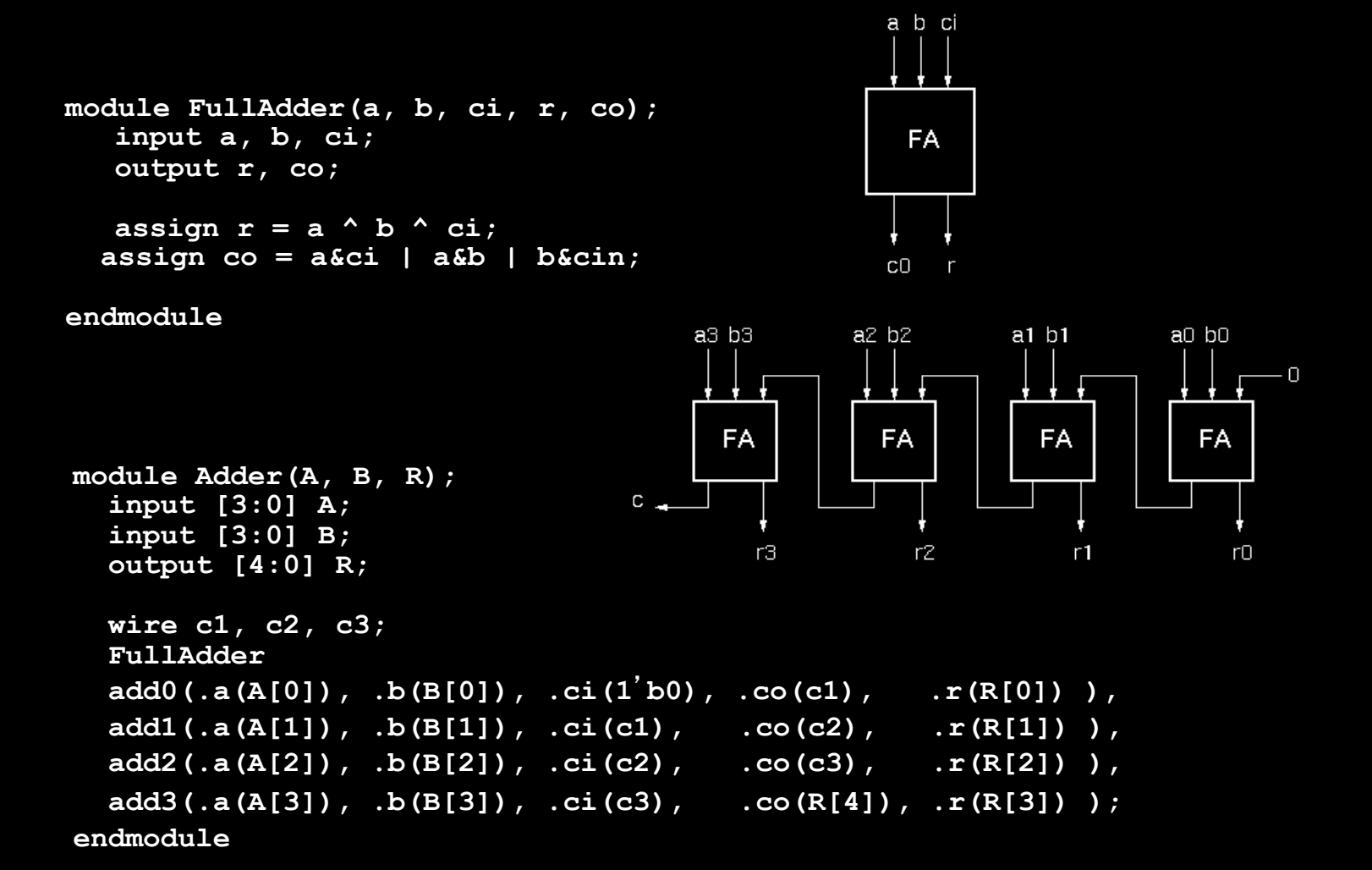
QQ_1725500302515

FullAdder 模块

module FullAdder(a, b, ci, r, co);
    input a, b, ci;      // 输入 a, b, 和进位 ci
    output r, co;        // 输出 r（和）和 co（进位）

    // 逻辑操作
    assign r = a ^ b ^ ci;       // r 是 a, b 和 ci 的异或结果
    assign co = a & b | a & ci | b & ci;  // co 是进位逻辑
endmodule

Adder 模块

module Adder(A, B, R);
    input [3:0] A, B;    // 输入 4 位二进制数 A 和 B
    output [4:0] R;      // 输出 5 位结果 R（包括进位）

    wire c1, c2, c3;     // 中间信号用于连接进位

    // 实例化四个全加器，构建 4 位加法器
    FullAdder add0 (.a(A[0]), .b(B[0]), .ci(1'b0), .co(c1), .r(R[0]));
    FullAdder add1 (.a(A[1]), .b(B[1]), .ci(c1), .co(c2), .r(R[1]));
    FullAdder add2 (.a(A[2]), .b(B[2]), .ci(c2), .co(c3), .r(R[2]));
    FullAdder add3 (.a(A[3]), .b(B[3]), .ci(c3), .co(R[4]), .r(R[3]));  // 最后的进位输出到 R[4]
endmodule

说明：

FullAdder 实现了基本的 1 位全加器，输出和 r 和进位 co。
Adder 通过实例化四个 FullAdder 实现了 4 位加法器，输入为 4 位数 A 和 B，输出为 5 位结果 R，其中包含最后的进位。

Verilog Operators & Logic Values

Verilog 提供了丰富的操作符来进行逻辑和算术操作。下表列出了常用的 Verilog 操作符及其功能分类，包括示例和解释：

操作符	名称	功能分类	示例代码	说明
`[]`	位选择（bit-select）或部分选择（part-select）	选择操作	`A[3]`	选择信号 `A` 的第 3 位。
`()`	括号（parenthesis）	优先级控制	`(A + B) * C`	使用括号改变运算顺序。
`!`	逻辑取反（logical negation）	逻辑操作	`!A`	如果 `A` 为 1，取反结果为 0，反之亦然。
`~`	按位取反（negation）	按位操作	`~A`	对 `A` 的每个位进行按位取反操作。
`&`	归约与（reduction AND）	归约操作	`&A`	对 `A` 的所有位进行与操作，结果是 1 或 0。
`\|`	归约或（reduction OR）	归约操作	`\|A`	对 `A` 的所有位进行或操作，结果是 1 或 0。
`~&`	归约与非（reduction NAND）	归约操作	`~&A`	先对 `A` 的所有位进行与操作，再取反。
`~\|`	归约或非（reduction NOR）	归约操作	`~\|A`	先对 `A` 的所有位进行或操作，再取反。
`^`	归约异或（reduction XOR）	归约操作	`^A`	对 `A` 的所有位进行异或操作。
`~^` 或 `^~`	归约同或（reduction XNOR）	归约操作	`~^A` 或 `^~A`	对 `A` 的所有位进行同或操作（异或后取反）。
`+`	一元正号（unary plus）	算术操作	`+A`	对 `A` 进行一元正号操作（通常省略）。
`-`	一元负号（unary minus）	算术操作	`-A`	对 `A` 取负值。
`{}`	拼接（concatenation）	拼接操作	`{A, B}`	将 `A` 和 `B` 拼接成一个更宽的信号。
{{ }}	复制（replication）	复制操作	{{4{A}}}	将 `A` 复制 4 次并拼接成一个信号。
`*`	乘法（multiply）	算术操作	`A * B`	`A` 乘以 `B`。
`/`	除法（divide）	算术操作	`A / B`	`A` 除以 `B`。
`%`	取模（modulus）	算术操作	`A % B`	`A` 除以 `B` 的余数。
`+`	二元加法（binary plus）	算术操作	`A + B`	`A` 加上 `B`。
`-`	二元减法（binary minus）	算术操作	`A - B`	`A` 减去 `B`。
`<<`	左移（shift left）	移位操作	`A << 2`	将 `A` 的所有位向左移动 2 位。
`>>`	右移（shift right）	移位操作	`A >> 2`	将 `A` 的所有位向右移动 2 位。
`>`	大于（greater than）	关系运算	`A > B`	判断 `A` 是否大于 `B`，返回 1 或 0。
`>=`	大于或等于（greater than or equal to）	关系运算	`A >= B`	判断 `A` 是否大于或等于 `B`，返回 1 或 0。
`<`	小于（less than）	关系运算	`A < B`	判断 `A` 是否小于 `B`，返回 1 或 0。
`<=`	小于或等于（less than or equal to）	关系运算	`A <= B`	判断 `A` 是否小于或等于 `B`，返回 1 或 0。
`==`	逻辑相等（logical equality）	等值判断	`A == B`	判断 `A` 是否等于 `B`，返回 1 或 0。
`!=`	逻辑不等（logical inequality）	等值判断	`A != B`	判断 `A` 是否不等于 `B`，返回 1 或 0。
`===`	条件相等（case equality）	等值判断	`A === B`	完全比较，包括 `x` 和 `z` 值。
`!==`	条件不等（case inequality）	等值判断	`A !== B`	完全比较，判断 `A` 和 `B` 是否不相等。
`&`	按位与（bit-wise AND）	按位操作	`A & B`	对 `A` 和 `B` 的每个位进行与操作。
`^`	按位异或（bit-wise XOR）	按位操作	`A ^ B`	对 `A` 和 `B` 的每个位进行异或操作。
`~^` 或 `^~`	按位同或（bit-wise XNOR）	按位操作	`A ~^ B` 或 `A ^~ B`	对 `A` 和 `B` 的每个位进行异或后取反。
`\|`	按位或（bit-wise OR）	按位操作	`A \| B`	对 `A` 和 `B` 的每个位进行或操作。
`&&`	逻辑与（logical AND）	逻辑操作	`A && B`	如果 `A` 和 `B` 均为 1，则返回 1，否则返回 0。
`\|\|`	逻辑或（logical OR）	逻辑操作	`A \|\| B`	如果 `A` 或 `B` 为 1，则返回 1，否则返回 0。
`? :`	条件（三元运算符）（conditional）	条件操作	`A ? B : C`	如果 `A` 为 1，结果为 `B`，否则结果为 `C`。

每个操作符都有其特定的用法，在 Verilog 设计中，通过这些操作符可以实现逻辑控制、位操作、算术运算以及条件判断等功能。

Continuous Assignment Examples

Verilog 中的连续赋值语句（assign）用于持续地计算和更新信号的值。以下是一些典型的连续赋值示例，展示了不同的操作符和用法。

wire [3:0] A, X, Y, R, Z;    // 定义 4 位宽的信号
wire [7:0] P;                // 定义 8 位宽的信号
wire r, a, cout, cin;        // 定义单个位宽的信号

示例代码	解释
`assign R = X \| (Y & ~Z);`	使用按位布尔操作符，按位与、按位或和按位取反，计算 `X`、`Y` 和 `Z`。
`assign r = &X;`	归约操作符：对 `X` 进行按位与操作，结果是单个位。
`assign R = (a == 1'b0) ? X : Y;`	条件操作符：如果 `a` 为 0，则 `R = X`，否则 `R = Y`。
`assign P = 8'hff;`	使用常量，`P` 被赋值为 8 位的十六进制常量 `ff`。
`assign P = X * Y;`	算术操作符：乘法运算（需要小心使用，可能涉及更多硬件资源）。
`assign P[7:0] = {4{X[3]}}, X[3:0];`	位拼接（Bit Field Concatenation），将 `X[3]` 扩展4位，然后拼接 `X` 的下4位。
`assign {cout, R} = X + Y + cin;`	加法操作，计算结果并包含进位。
`assign Y = A << 2;`	移位操作符：左移 2 位，结果为 `A` 的每个位左移 2 位。
`assign Y = {A[1], A[0], 1'b0, 1'b0};`	等效的位移操作，通过手动指定位，等效于 `A << 2`。

说明：

按位布尔操作符：按位与（&）、按位或（|）、按位取反（~）用于逐位计算信号。
归约操作符：例如 &X 将 X 中的每个位与在一起，产生一个单个位的输出。
条件操作符（三元操作符）： (condition) ? true_case : false_case，根据条件选择值。
算术操作符：乘法、加法等算术运算可以直接在信号上操作，但要注意硬件资源的消耗。
移位操作符：<< 和 >> 分别表示左移和右移，通常用于位级操作。

Review

Design Metrics

设计评估指标主要涵盖以下几个方面：

功能性和鲁棒性（Functionality and Robustness）：确保设计正确实现预期功能，并且在不同条件下能稳定运行。
成本（Cost）：控制制造、开发和运行的总成本。
性能（Performance）：衡量设计的速度和效率，特别是在计算密集型应用中。
功率与能耗（Power and Energy）：能效在现代设备中至关重要，特别是在移动设备和高性能计算中。

Verilog

硬件描述语言（HDL）：Verilog 是一种用于描述硬件设计的语言，帮助设计者通过代码方式定义电路结构和行为。
逻辑综合：Verilog 代码会被转换为门级网表（Gate-level netlists），用于进一步的硬件实现。
ASIC 和 FPGA：Verilog 被广泛应用于专用集成电路（ASIC）和现场可编程门阵列（FPGA）设计中。
连续赋值语句：assign 语句允许设计者定义电路中的逻辑关系，自动且持续地更新信号。