Lecture 5 Combinational Logic I

Review of Verilog

Verilog

Verilog 是一种硬件描述语言（HDL），用于描述数字电路的结构和行为。在 EECS 151/251A 中，Verilog 被广泛用于设计和实现复杂的数字系统。

• 硬件描述语言（HDL）：Verilog 主要用于描述硬件的结构和功能，它通过代码精确表达电路的逻辑设计。
• 逻辑综合（Logic Synthesis）：Verilog 代码可以通过综合工具转化为门级网表（Gate-level Netlist），从而实现硬件设计的物理实现。

Verilog 在 ASIC 和 FPGA 设计中的应用

Verilog 被广泛应用于 ASIC（专用集成电路）和 FPGA（现场可编程门阵列）设计中，能够灵活描述硬件结构并生成可综合的网表。

• 模块化设计（Modules）：Verilog 的模块化设计允许将复杂的电路划分为多个模块，便于管理和重用。
• 结构化与行为化描述（Structural vs Behavioral）：Verilog 支持两种建模方式。结构化建模专注于电路组件的连接，而行为化建模描述电路的功能行为。
• 操作符与逻辑值（Operators and Logic Values）：Verilog 提供丰富的逻辑操作符来进行逻辑运算和控制信号流。

组合逻辑电路（Combinational Circuits）

组合逻辑电路的输出仅取决于当前输入，而不依赖于时钟或状态。Verilog 提供了两种主要方法来实现组合逻辑：

• assign 语句：使用 assign 定义简单的组合逻辑，适用于实时计算。
• always 块：当需要更复杂的逻辑时，可以使用 always @(*) 块，这样可以实现条件判断和多路选择器等功能。

时序逻辑电路（Sequential Circuits）

时序逻辑电路不仅依赖于当前输入，还依赖于时钟和电路的状态。Verilog 使用 always @(posedge clk) 描述时序逻辑，其中的状态由时钟驱动更新。

• always 块：在时钟的上升沿或下降沿触发，用于描述触发器和寄存器等电路的行为。
• 阻塞与非阻塞赋值（Blocking vs NonBlocking Assignment）：
  • 阻塞赋值：使用 = 立即更新信号，适用于组合逻辑。
  • 非阻塞赋值：使用 <= 进行同步更新，适用于时序逻辑，确保所有信号在同一个时钟周期结束时同时更新。

通过这些机制，Verilog 提供了强大的功能来描述和实现数字系统的组合和时序逻辑。

Combinational Logic

组合逻辑概述

组合逻辑是数字电路设计中的一种基本逻辑类型，其输出仅依赖于当前的输入值，而不涉及任何内部存储状态。这种逻辑能够直接根据输入信号计算出输出值。

主要特点

• 无记忆特性（Memoryless）：组合逻辑电路不存储任何先前的输入或输出状态。输出仅与当前的输入有关。
• 即时响应：当输入信号变化时，输出会立即变化（实际上会有一个依赖于实现的微小延迟，但可以忽略不计）。

例如，在下图中，组合逻辑电路接受 x0, x1, ..., xn-1 作为输入，产生 y0, y1, ..., ym-1 作为输出。输入信号变化后，输出将根据组合逻辑电路的功能立即更新。

组合逻辑应用

组合逻辑广泛用于诸如加法器、多路选择器、解码器等无状态电路中，适用于各种瞬时计算场景。

Combinational Logic Example

逻辑示例

如图所示，一个组合逻辑电路接受两个输入 a 和 b，输出 out。通过 布尔代数（Boolean Algebra） 可以推导出其逻辑关系。

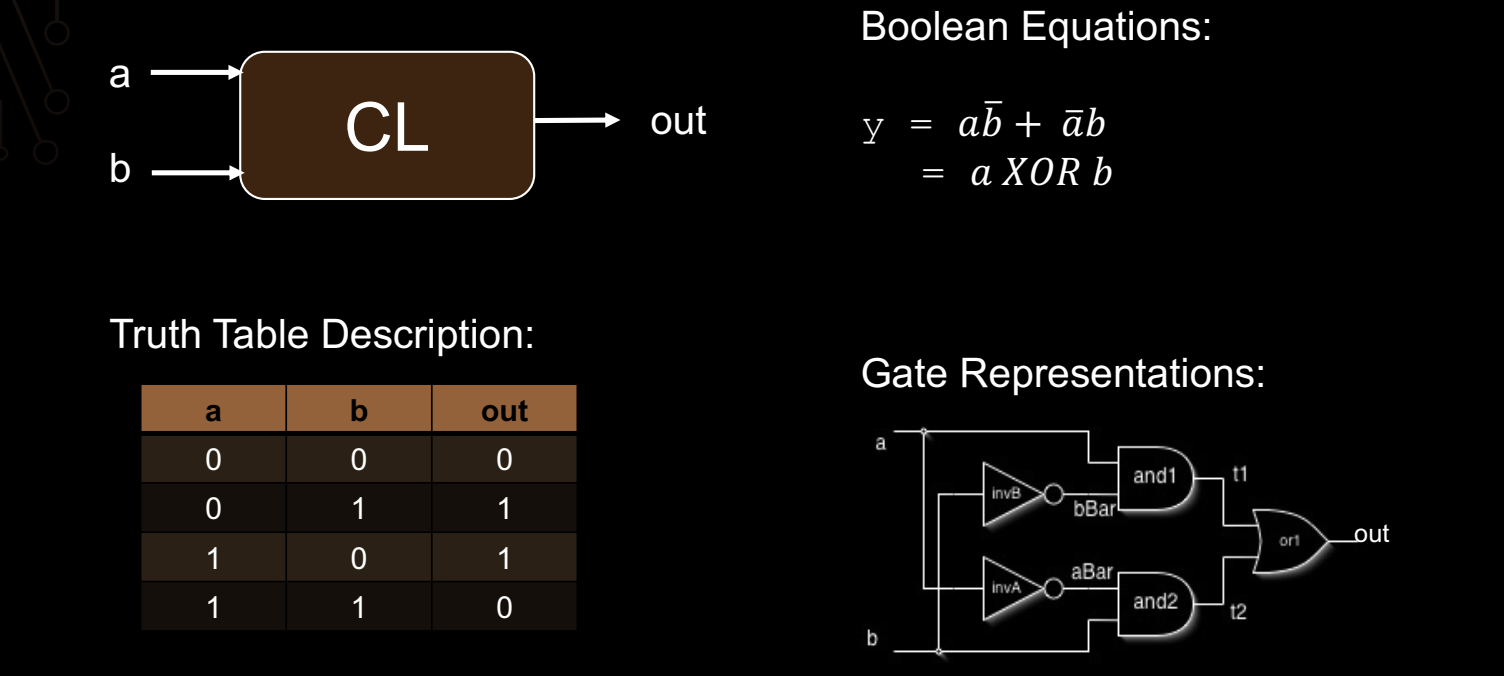
布尔表达式

通过观察真值表，可以写出对应的布尔表达式。这里的输出 y 是 a 和 b 的 异或（XOR） 运算：

\[ y = a\overline{b} + \overline{a}b = a \oplus b \]

真值表

通过真值表可以总结输入与输出的对应关系：

a	b	out
0	0	0
0	1	1
1	0	1
1	1	0

门电路表示

逻辑可以用逻辑门的电路图来表示：a 和 b 通过 与非门（NAND） 和 与门（AND） 等组合后，生成输出 y。在该例子中，通过 NOT、AND 和 OR 门电路组合来实现 XOR 运算。

这个例子展示了如何通过布尔代数推导出逻辑表达式，使用真值表验证逻辑，并通过逻辑门实现该逻辑功能。

Relationship Among Representations

在组合逻辑设计中，有三种常见的表示方法，它们互相关联，帮助我们从不同角度理解逻辑电路：

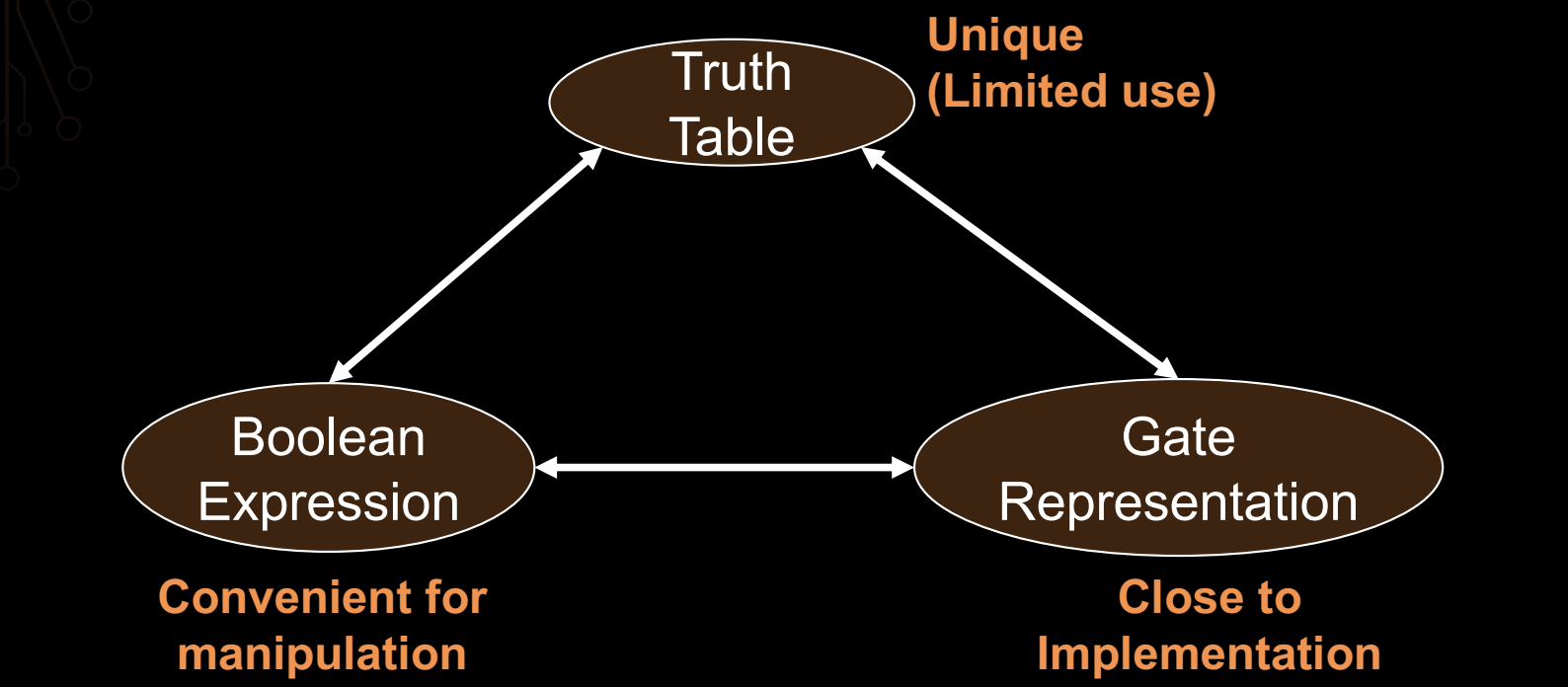
1. 真值表（Truth Table）：通过列出所有可能的输入组合，显示出每种输入对应的输出。这种表示唯一且适合有限输入情况，但规模会随着输入数量增加而迅速扩大。

2. 布尔表达式（Boolean Expression）：基于逻辑运算符（如 AND、OR、NOT 等）来表示逻辑功能。它易于操作和化简，尤其适合代数运算。

3. 门电路表示（Gate Representation）：接近硬件实现，使用逻辑门如 AND、OR、NOT 来描述逻辑电路的实际结构。

这些表示方法可以互相转换，真值表可以转换成布尔表达式，而布尔表达式可以进一步转换为门电路表示。

Boolean Algebra Background

逻辑电路的名称源于它们所基于的逻辑学原理。19世纪数学家 George Boole 开创了基于逻辑的代数系统——布尔代数（Boolean Algebra）。布尔代数使用两个变量：TRUE 和 FALSE（1 和 0），表示逻辑状态。

1937年，信息论之父 Claude Shannon 在其硕士论文中，首次展示了如何将布尔代数映射到数字电路中。这一突破成为现代数字电路设计的基础，奠定了逻辑电路理论的根基。

Boolean Algebra Fundamentals

布尔代数有三个基本元素：

1. 二元变量（Binary Variables）：元素为 0 和 1，分别表示逻辑上的 False 和 True。

2. 二元运算符（Binary Operators）：
   • AND（·）：逻辑与，输出为 1 仅当所有输入都为 1 时。
   • OR（+）：逻辑或，输出为 1 只要任意输入为 1。
3. 一元运算符（Unary Operator）：
   • NOT（ ̅）：逻辑非，将输入反转，1 变为 0，0 变为 1。

示例逻辑门与真值表

• AND 门：当 X 和 Y 都为 1 时，Z 输出为 1。

• 

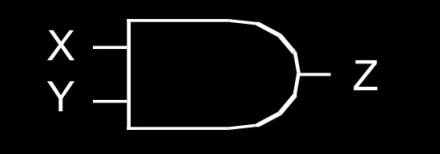
  X	Y	Z
  0	0	0
  0	1	0
  1	0	0
  1	1	1

• OR 门：只要 X 或 Y 为 1，Z 输出为 1。

• 

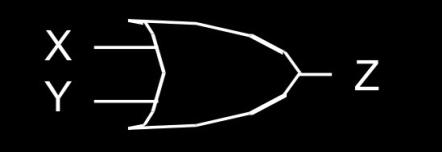
  X	Y	Z
  0	0	0
  0	1	1
  1	0	1
  1	1	1

• NOT 门：输入 X 的反转。

• 

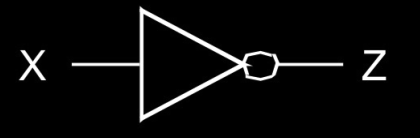
  X	Z
  0	1
  1	0

这些基础运算是所有数字电路和逻辑运算的核心，它们通过不同组合构成复杂的逻辑电路。

Boolean Operations of 2 Variables

对于两个变量 X 和 Y，可以构造出 16 种不同的布尔逻辑函数。这些函数可以通过真值表来表示，表明不同输入组合下的输出。

布尔表达式	逻辑函数名称	解释
\( F_0 = 0 \)	恒等式零	输出始终为 0。
\( F_1 = X \cdot Y \)	逻辑与（AND）	当且仅当 \( X \) 和 \( Y \) 均为 1 时，输出为 1。
\( F_2 = X \cdot \overline{Y} \)	条件 AND	当 \( X = 1 \) 且 \( Y = 0 \) 时，输出为 1。
\( F_3 = X \)	恒等于 X	输出等于 \( X \) 的值，无论 \( Y \) 的值如何。
\( F_4 = \overline{X} \cdot Y \)	条件 AND	当 \( X = 0 \) 且 \( Y = 1 \) 时，输出为 1。
\( F_5 = Y \)	恒等于 Y	输出等于 \( Y \) 的值，无论 \( X \) 的值如何。
\( F_6 = X \oplus Y \)	异或（XOR）	当 \( X \) 和 \( Y \) 的值不同时，输出为 1。
\( F_7 = X + Y \)	逻辑或（OR）	当 \( X \) 或 \( Y \) 为 1 时，输出为 1。
\( F_8 = \overline{X + Y} \)	逻辑或非（NOR）	OR 的反，当 \( X \) 和 \( Y \) 均为 0 时，输出为 1。
\( F_9 = \overline{X \oplus Y} \)	同或（XNOR）	当 \( X \) 和 \( Y \) 相同时，输出为 1。
\( F_A = \overline{Y} \)	Y 的取反（NOT Y）	输出等于 \( Y \) 的反值，当 \( Y = 0 \) 时，输出为 1；当 \( Y = 1 \) 时，输出为 0。
\( F_B = 1 \)	恒等式一	输出始终为 1。
\( F_C = \overline{X} \)	X 的取反（NOT X）	输出等于 \( X \) 的反值，当 \( X = 0 \) 时，输出为 1；当 \( X = 1 \) 时，输出为 0。
\( F_D = \overline{X \cdot Y} \)	与非（NAND）	AND 的反，当 \( X = 1 \) 且 \( Y = 1 \) 时，输出为 0。
\( F_E = \overline{X + Y} \)	或非（NOR）	OR 的反，当 \( X = 0 \) 且 \( Y = 0 \) 时，输出为 1。
\( F_F = 1 \)	恒等式一	输出始终为 1。

布尔运算的真值表

真值表列出了 \( X \) 和 \( Y \) 的四种组合输入值，并列出了每种输入情况下的 16 种逻辑函数 \( F_0 \) 到 \( F_F \) 的输出。这些函数包括常见的逻辑操作如 AND、OR、XOR、NAND、NOR 等。

Decomposition in Digital Design

在数字设计中，随着输入变量的增加，真值表的行数以 2^n 的速度增长。例如，若输入有 n 个，则需要 2^n 行来表示所有可能的输入组合。

示例：4 位加法器

• 加法器接收两个 4 位输入 A 和 B，并输出和 R 和进位 c。
• 对于 4 位输入的真值表，每个输入可能组合总共有 2^8 = 256 行。这意味着所有可能的输入组合以及对应的输出需要在 256 行的真值表中进行描述。

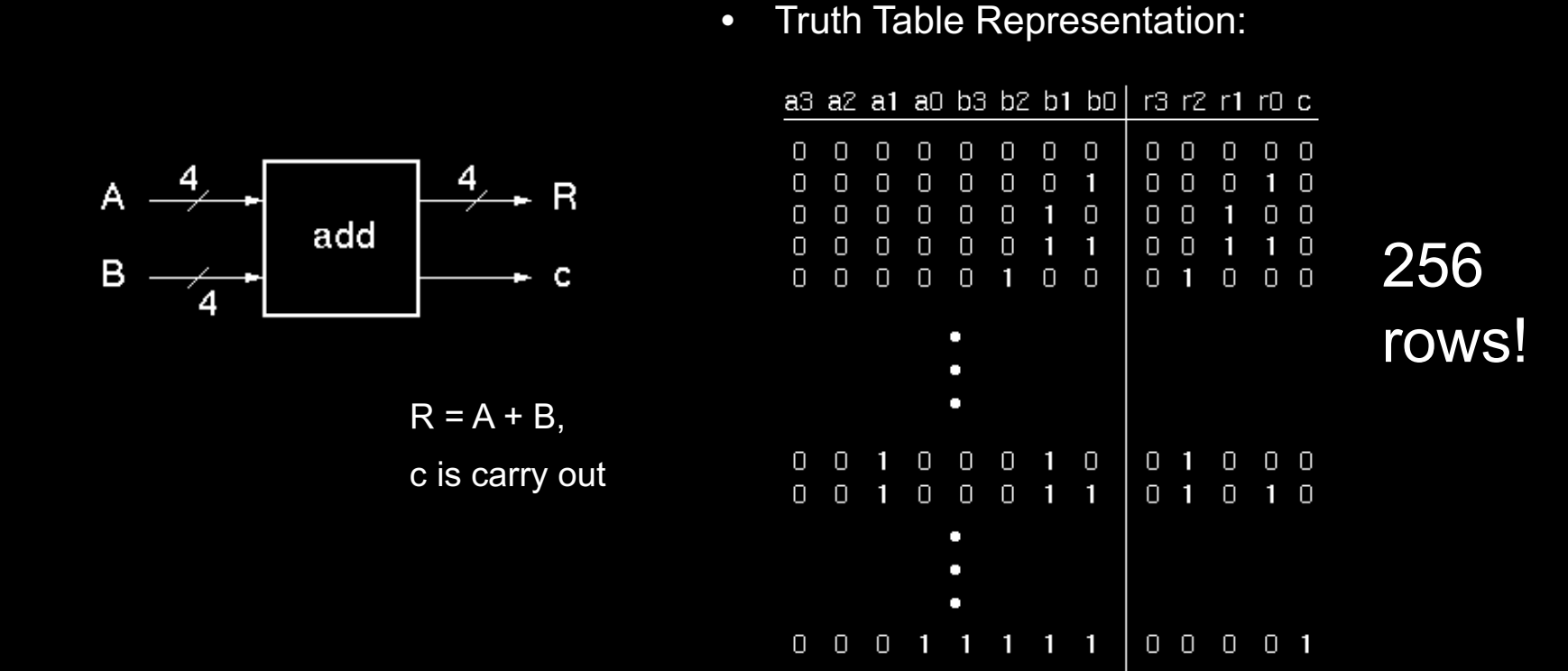
数字设计中的加法器设计可以通过手动计算逐步理解其逻辑运作。在该过程中，输入的每一位相加会生成一个和（sum）和进位（carry），这些操作可以通过布尔代数进行分解并实现。

1. 二进制加法器的基本逻辑

我们从两位二进制数的加法开始，例如：

• a₀ 和 b₀ 的加法：
  • 和（r）：r = a ⊕ b （异或运算）
  • 进位（c）：c = a ∙ b （与运算）

真值表描述了这种加法操作的所有可能组合：

a	b	c (进位)	r (和)
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

这里的 异或（XOR） 运算决定了和，而 与（AND） 运算则决定了进位。

2. 二位进位加法器的扩展

当我们对更高位进行加法时，需要考虑前一位的进位。以下是 a₁ 和 b₁ 的加法情况，结合来自 a₀ 和 b₀ 的进位：

cᵢ (进位)	a	b	cₒ (输出进位)	r (和)
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

布尔表达式如下：

• 和（r）：r = a ⊕ b ⊕ cᵢ
• 输出进位（cₒ）：cₒ = a ∙ b + (a + b) ∙ cᵢ

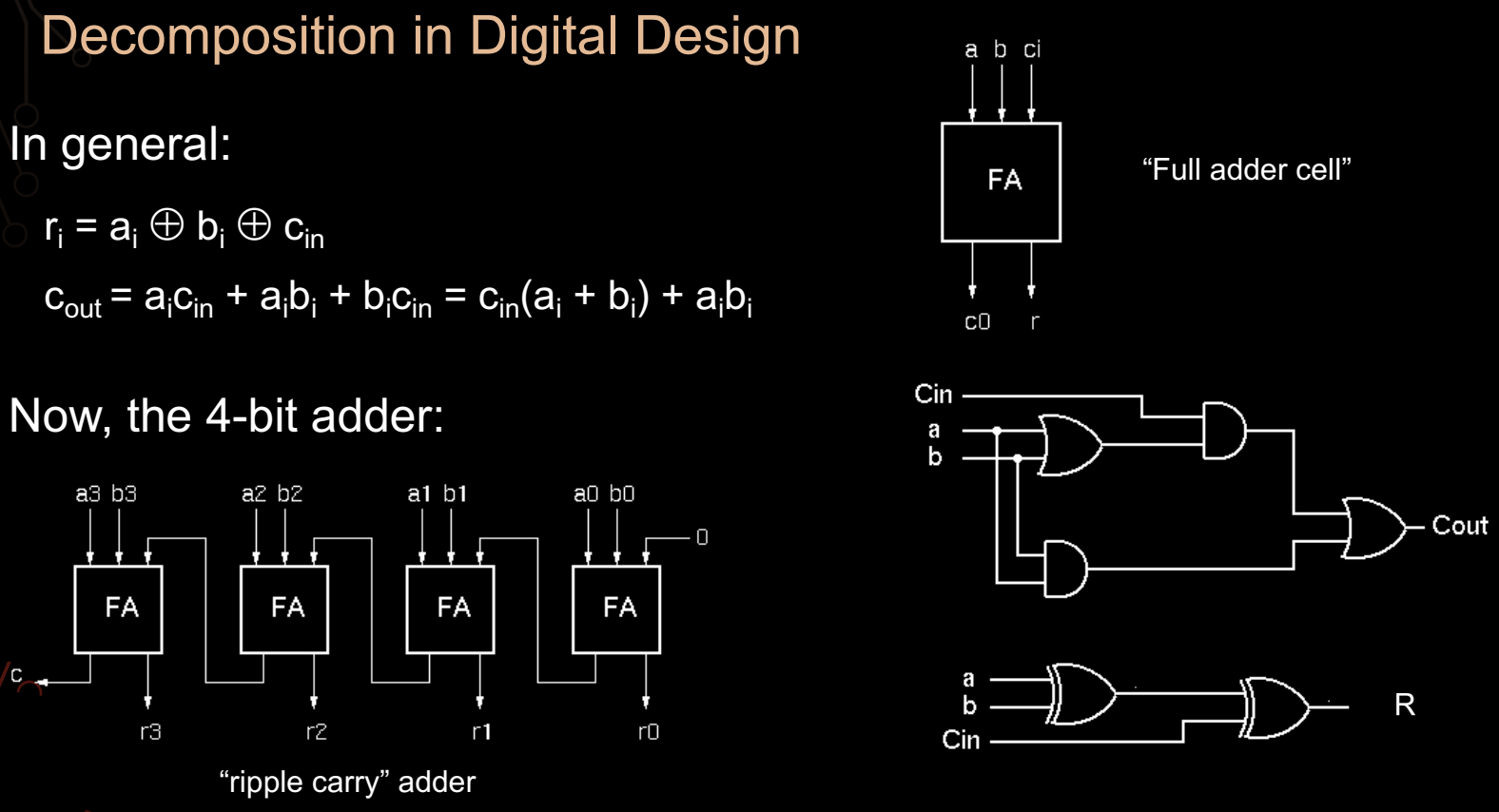
3. 4 位 Ripple-Carry 加法器

为了处理更高位的加法，如 4 位加法器，我们可以将多个全加器（Full Adder）级联起来形成 纹波进位加法器（Ripple-Carry Adder）。每个全加器接收两个输入位（aᵢ 和 bᵢ），以及来自前一位的进位 cᵢ，并生成和 rᵢ 和输出进位 cₒ。

• 一般公式：
  • 和（rᵢ）：rᵢ = aᵢ ⊕ bᵢ ⊕ cᵢ
  • 输出进位（cₒ）：cₒ = aᵢ ∙ bᵢ + (aᵢ + bᵢ) ∙ cᵢ

该结构使得进位信号逐步传播，最终决定最高位的加法结果。

4. Ripple-Carry 加法器结构

图中展示了 4 位 Ripple-Carry 加法器的结构：

• 每个 全加器单元（FA） 处理一位输入，并将进位传递给下一位。
• Cin 是输入的初始进位，通常为 0。每个全加器生成的 Cout 作为下一个全加器的 Cin 输入。

通过这种方式，可以处理任意位宽的加法运算。

Laws of Boolean Algebra

布尔代数是组合逻辑设计的核心，它为逻辑电路的设计提供了数学基础。通过布尔代数的定律，我们可以简化和优化逻辑表达式，从而实现更高效的电路设计。以下是布尔代数的主要定律：

1. 恒等律（Identities）

• X + 0 = X: OR 操作中，任何值与 0 相或，结果都是该值本身。
• X ∙ 1 = X: AND 操作中，任何值与 1 相与，结果也是该值本身。
• 这些恒等律帮助我们在不改变逻辑功能的情况下简化表达式。

2. 幂等律（Idempotence）

• X + X = X: OR 操作中，任何值与自己相或，结果不变。
• X ∙ X = X: AND 操作中，任何值与自己相与，结果也不变。
• 幂等律表明在逻辑表达式中，重复的相同变量不会改变输出，这可以进一步减少冗余逻辑。

3. 互补律（Complements）

• X + X’ = 1: OR 操作中，变量与其反转值相或，结果为 1。
• X ∙ X’ = 0: AND 操作中，变量与其反转值相与，结果为 0。
• 互补律用于表达相反的逻辑状态，在构建复杂逻辑时非常有用。

4. 交换律（Commutative Law）

• X + Y = Y + X: OR 操作是可交换的。
• X ∙ Y = Y ∙ X: AND 操作也是可交换的。
• 交换律允许我们在表达式中自由地交换操作数顺序，而不会改变结果。

5. 结合律（Associative Law）

• (X + Y) + Z = X + (Y + Z): 多个 OR 操作可以任意组合。
• (X ∙ Y) ∙ Z = X ∙ (Y ∙ Z): 多个 AND 操作也可以任意组合。
• 结合律使我们可以更灵活地重组表达式，以便于实现。

6. 分配律（Distributive Law）

• X ∙ (Y + Z) = (X ∙ Y) + (X ∙ Z): AND 操作对 OR 操作分配。
• X + (Y ∙ Z) = (X + Y) ∙ (X + Z): OR 操作对 AND 操作分配。
• 分配律是布尔代数中最重要的定律之一，它允许我们重新排列并简化表达式，特别是在构建电路时，可以减少所需逻辑门的数量。

7. 对偶律（Duality）

• AND 和 OR 互换: 对偶律说明可以将 AND 操作替换为 OR 操作，反之亦然，同时将 0 替换为 1，1 替换为 0，而不改变表达式的结构。
• 例如，对于表达式 X ∙ 1 = X，其对偶是 X + 0 = X。
• 对偶律帮助我们理解逻辑运算中的对称性，尤其是在反转逻辑设计中起到关键作用。

DeMorgan’s Law

德摩根定律（DeMorgan’s Law） 是布尔代数中极为重要的一部分，它描述了反转逻辑运算的关系，提供了一种将与和或操作互换的方法。

德摩根定律的两个形式：

1. 第一条德摩根定律

\[ \overline{X \cdot Y} = \overline{X} + \overline{Y} \]

与操作的反转等于两个输入的反操作的或。

对应的逻辑电路表示：

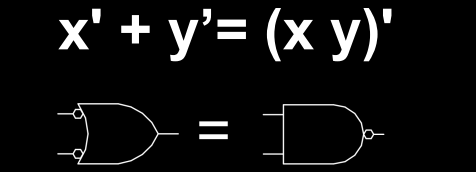
与门的反转可以通过或门实现，并对输入取反。反过来也可以。

2. 第二条德摩根定律

\[ \overline{X + Y} = \overline{X} \cdot \overline{Y} \]

或操作的反转等于两个输入的反操作的与。

对应的逻辑电路表示：

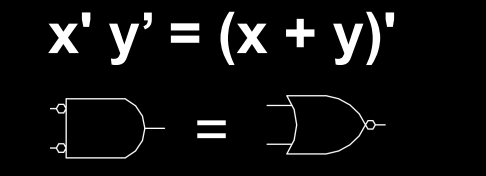
或门的反转可以通过与门实现，并对输入进行取反。反过来也可以。

德摩根定律在逻辑设计中非常有用，特别是当需要通过反转来转换复杂的逻辑表达式时。通过使用这两条定律，我们可以更有效地优化电路，减少不必要的逻辑门。

应用德摩根定律的真值表

在德摩根定律的示例中，通过真值表我们可以直观地观察到逻辑等式的正确性：

1. 第一条德摩根定律：

   • 真值表展示了 \(\overline{X \cdot Y}\) 和 \(\overline{X} + \overline{Y}\) 的输出结果相同。

     

2. 第二条德摩根定律：

   • 真值表展示了 \(\overline{X + Y}\) 和 \(\overline{X} \cdot \overline{Y}\) 的输出结果相同。

     

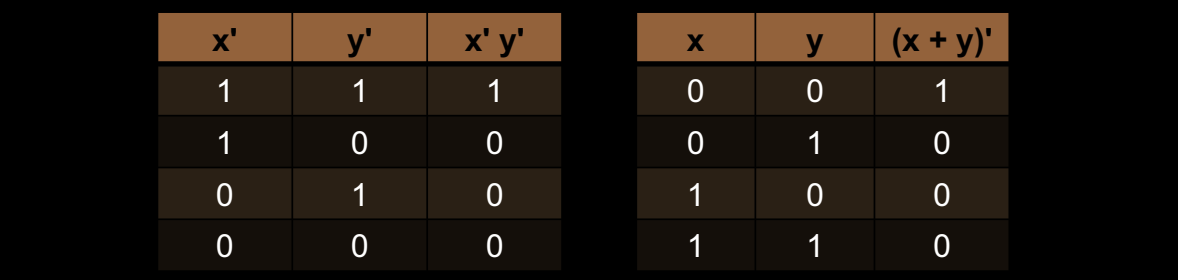
通过这些真值表可以清晰地验证德摩根定律的正确性。这些定律在逻辑电路设计中的应用非常广泛，尤其是在需要简化和优化电路时。

德摩根定律的应用

在逻辑设计中，德摩根定律不仅是简化逻辑表达式的重要工具，还能帮助我们通过 NAND 或 NOR 门实现逻辑电路。由于 NAND 和 NOR 门在硬件实现上往往比其他逻辑门更简单和高效，德摩根定律为设计者提供了优化和转换逻辑电路的有效途径。

逻辑转换示例：从 AND/OR 到 NAND/NOR

1. NAND 等效转换：
   • 一个 NAND 门等价于一个 OR 门，其输入取反。
   • 即，\(\overline{X \cdot Y}\) 可以通过将两个输入分别经过 NOT 门后输入到 OR 门来实现。
2. NOR 等效转换：
   • 一个 NOR 门等价于一个 AND 门，其输入取反。
   • 即，\(\overline{X + Y}\) 可以通过将两个输入分别经过 NOT 门后输入到 AND 门来实现。

这种转换非常有用，因为 NAND 和 NOR 门是功能完备的逻辑门，可以用于构建任何数字电路。因此，能够利用德摩根定律将常规的 AND 和 OR 逻辑门转化为 NAND 和 NOR 门，能够大大简化硬件设计。

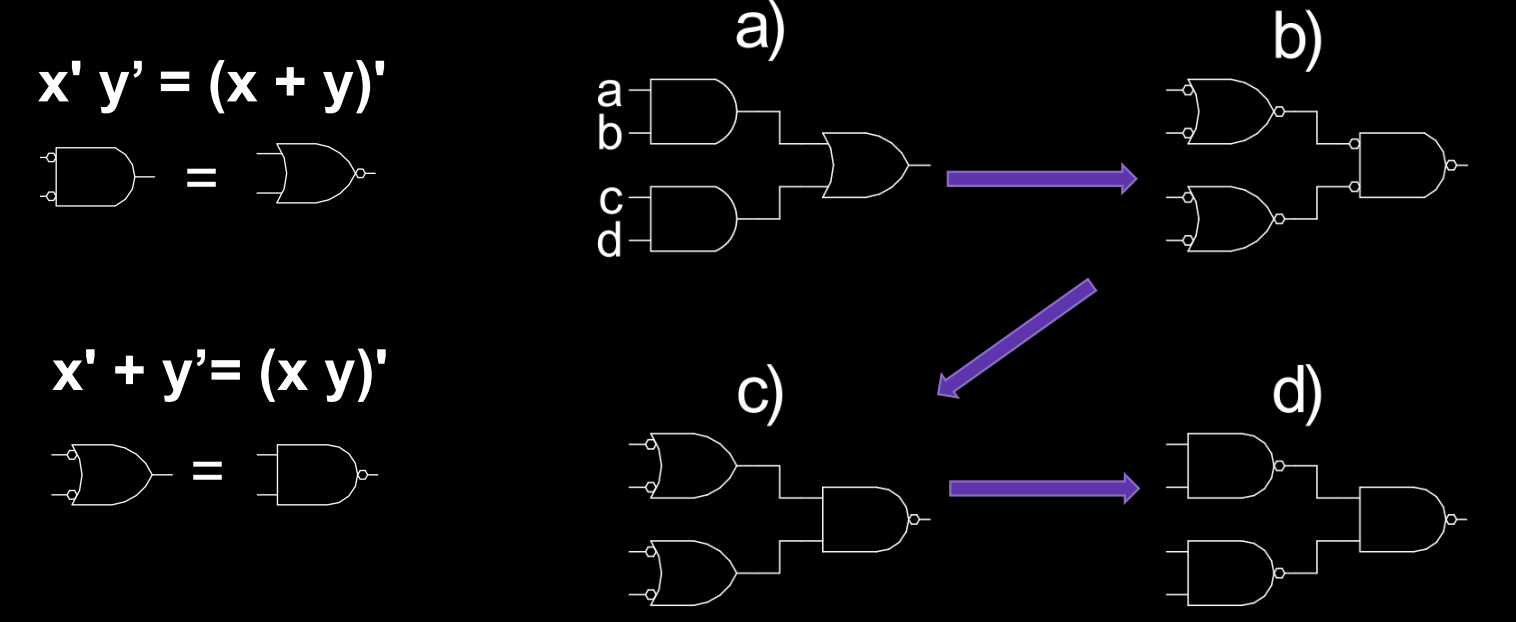
泡推技术（Bubble Pushing）

泡推（Bubble Pushing） 是德摩根定律在电路设计中的直观应用方式，用于在逻辑电路中移动“反相点”（泡）。这是一种视觉化的符号方法，通过将泡从电路的一侧“推”到另一侧，我们可以改变逻辑门的类型，而不改变电路的逻辑功能。

• 如果一个泡推到逻辑门的输入处，电路的功能相当于这个门的反操作。
• 例如，推泡会将 AND 门转换为 OR 门，反之亦然。

泡推技术示例：

• 在 AND 和 OR 门上，泡代表反操作，将泡从输入移动到输出时，逻辑门类型会发生翻转。
• 当泡从输入端移至输出时，AND 门会变为 OR 门，而 OR 门会变为 AND 门。

通过使用这种技术，设计者可以在保持电路逻辑功能不变的情况下，将电路转换为更适合硬件实现的形式。

德摩根定律不仅是布尔代数中的重要定律，也是数字电路设计中的重要工具。它允许我们通过简单的逻辑转换实现复杂电路的优化，并通过使用 NAND 和 NOR 门来降低硬件实现的复杂性。

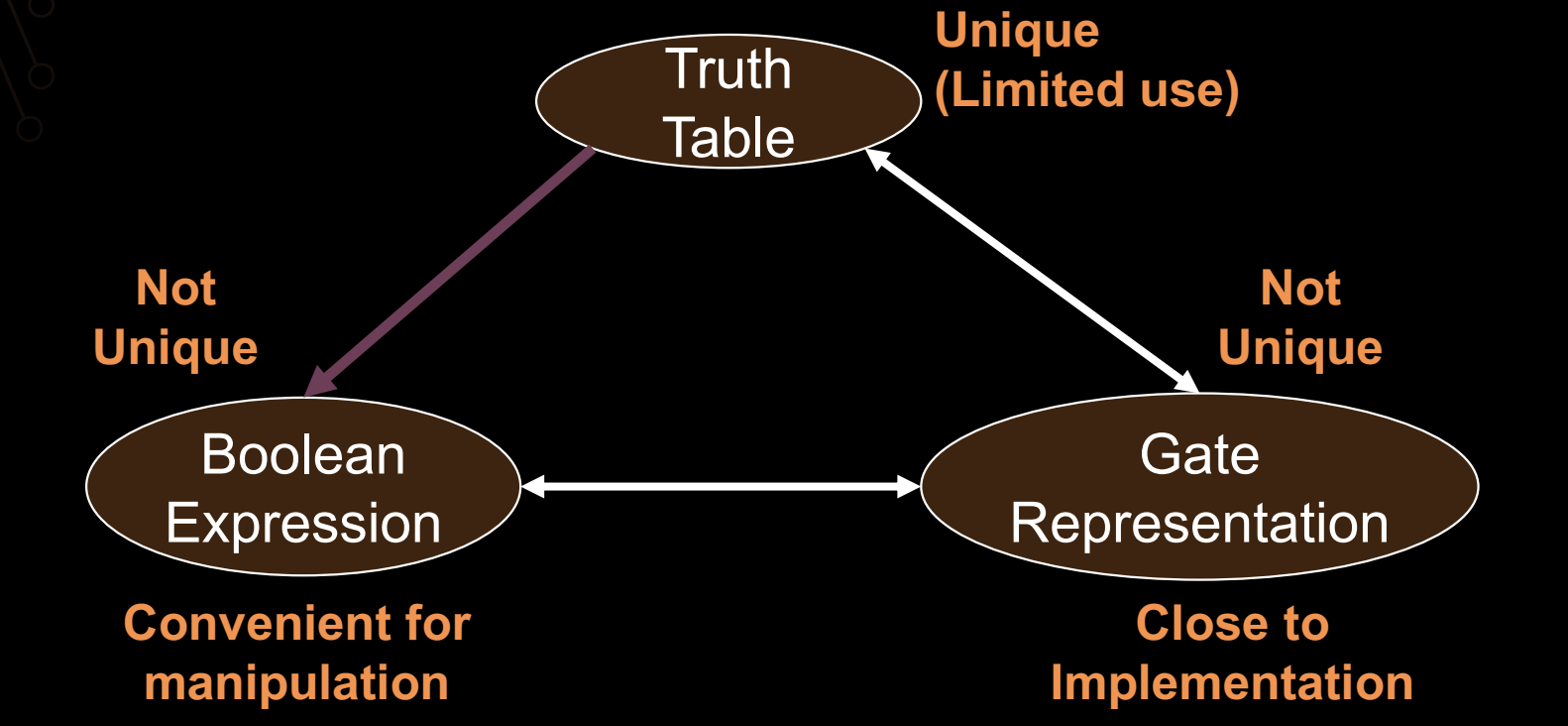
Relationship Among Representations2

在组合逻辑设计中，逻辑表达式、真值表和门电路的表示形式紧密相关。每种表示方式都在不同的设计阶段具有不同的用途，因此理解它们之间的关系非常重要。

1. 真值表（Truth Table）

• 真值表提供了逻辑电路所有可能的输入组合以及相应的输出。它是唯一的表示形式，直接展示了电路的行为。
• 虽然真值表易于理解，但它不便于直接实现复杂电路，因此在硬件设计中并不常用。

2. 布尔表达式（Boolean Expression）

• 布尔表达式基于布尔代数，通过逻辑运算符（如 AND、OR、NOT 等）来描述电路功能。
• 布尔表达式并不唯一。一个真值表可以对应多个不同的布尔表达式，经过不同的代数操作可以得到不同的表达式。
• 它是方便操纵的表示形式，常用于简化和优化电路。

3. 门电路表示（Gate Representation）

• 门电路表示是最接近硬件实现的方式。通过逻辑门（如 AND 门、OR 门、NOT 门等）的连接来实现布尔表达式。
• 与布尔表达式类似，门电路的实现也不是唯一的。设计者可以通过不同的逻辑门组合来实现相同的逻辑功能。

Canonical Forms

在逻辑设计中，规范形式（Canonical Forms） 是一种标准化的布尔表达式表示方法。通过从真值表转换得到，可以将复杂的逻辑表达式以更结构化的方式呈现。规范形式有两种主要类型：

1. 积之和形式（Sum of Products, SOP）

• SOP 是将布尔表达式以 AND 项（积）相加的形式展现的。每一项称为一个 最小项（Minterm），它表示在真值表中输出为 1 的输入组合。
• 最小项 是包含所有输入变量的与操作，只有当所有输入条件都满足时，最小项的输出为 1。
• SOP 常被称为析取范式（Disjunctive Normal Form），因为它是各最小项的析取（或）的结果。
• 例子：对于三个输入变量 a, b, c 的真值表，输出 f 的 SOP 形式可能是： \[ f = a’b’c + ab’c’ + abc \]

2. 和之积形式（Product of Sums, POS）

later

Sum of Products 例子

通过从真值表中的输出为 1 的行提取最小项，可以构造 SOP 表达式。每一项对应真值表中输出为 1 的一行，并使用 AND 连接每个输入的适当状态。

例如，对于下表：

Minterms	a	b	c	f	f’
a’b’c’	0	0	0	0	1
a’b’c	0	0	1	0	1
a’bc’	0	1	0	1	0
a’bc	0	1	1	1	0
ab’c’	1	0	0	1	0
ab’c	1	0	1	0	1
abc’	1	1	0	0	1
abc	1	1	1	1	0

在该真值表中，输出 f 为 1 的情况包括：

• 当 a'b'c 为真时
• 当 a'bc 为真时
• 当 ab'c' 为真时
• 当 abc 为真时

因此，SOP 表达式为： \[ f = a’b’c + a’bc + ab’c’ + abc \]

通过这种方式，可以将任意的真值表转换为 SOP 或 POS 表达式。这些规范形式在数字逻辑设计中极为有用，尤其是在生成布尔表达式时，用于简化和优化逻辑电路设计。

Quiz: Sum of Products Derivation

问题：

根据真值表推导出 \( \overline{Y} \) 的积之和（SOP）形式。

真值表：

A	B	Y	\( \overline{Y} \)
0	0	0	1
0	1	0	1
1	0	1	0
1	1	1	0

推导步骤：

从真值表可以看出，当 \( A = 0 \) 且 \( B = 0 \) 或者 \( A = 0 \) 且 \( B = 1 \) 时，\( \overline{Y} \) 输出为 1。因此，\( \overline{Y} \) 的积之和形式可以通过输出为 1 的行提取最小项得到。

积之和形式：

• 当 \( A = 0 \)，\( B = 0 \) 时，对应的最小项是 \( A’B’ \)。
• 当 \( A = 0 \)，\( B = 1 \) 时，对应的最小项是 \( A’B \)。

因此，\( \overline{Y} \) 的 SOP 形式为： \[ \overline{Y} = A’B’ + A’B \]

选项：

• a) \( \overline{Y} = (A + B)(A + \overline{B}) \)
• b) \( \overline{Y} = A’B’ + AB \)
• c) \( \overline{Y} = A’B’ + A’B \)

显然，选项 c) 是正确的答案，因为它符合从真值表推导出的 \( \overline{Y} \) 的积之和形式。

Simplifying Sum of Products

规范形式（Canonical Forms）：

虽然积之和形式是一种标准化的表示法，但它通常并不是最简化的形式。通过布尔代数规则，我们可以进一步简化这些表达式，使逻辑电路的实现更加高效。

简化示例：

通过使用布尔代数中的分配律和合并项，我们能够减少逻辑表达式中的项数，从而简化逻辑电路的实现。

布尔代数规则回顾：

定律	表达式	解释说明
消去律	\( x + x’y = x + y \)	当 \( x \) 和 \( x’ \) 两个变量相加时，只需考虑 \( y \)。这减少了表达式的复杂度。
结合律	\( (X + Y) + Z = X + (Y + Z) \)	OR 操作的结果不受括号的影响，适用于 AND 也一样。
	\( (X \cdot Y) \cdot Z = X \cdot (Y \cdot Z) \)
交换律	\( X + Y = Y + X \)	交换输入变量的顺序不会改变输出的结果，适用于 AND 和 OR。
	\( X \cdot Y = Y \cdot X \)
分配律	\( X + Y \cdot Z = (X + Y) \cdot (X + Z) \)	逻辑 OR 和 AND 可以根据需要进行分配，类似于算术中的乘法分配律。
	\( X \cdot (Y + Z) = X \cdot Y + X \cdot Z \)
幂等律	\( X + X = X \)	变量与自身 OR 或 AND 时，结果等于自身。
	\( X \cdot X = X \)
单位元律	\( X + 0 = X \)	OR 操作中，任何变量与 0 相加结果是变量自身。
	\( X \cdot 1 = X \)	AND 操作中，任何变量与 1 相乘结果是变量自身。
零律	\( X \cdot 0 = 0 \)	AND 操作中，任何变量与 0 相乘结果为 0。
	\( X + 1 = 1 \)	OR 操作中，任何变量与 1 相加结果为 1。
补元律	\( X + X’ = 1 \)	任何变量与其反值的 OR 结果是 1。
	\( X \cdot X’ = 0 \)	任何变量与其反值的 AND 结果是 0。
双重否定律	\( (X’)’ = X \)	变量取两次反结果是变量自身。
德摩根律	\( (X \cdot Y)’ = X’ + Y’ \)	AND 的反值等于各变量的 OR 反值。
	\( (X + Y)’ = X’ \cdot Y’ \)	OR 的反值等于各变量的 AND 反值。
吸收律	\( X + X \cdot Y = X \)	将逻辑表达式简化的定律之一，适用于减少冗余变量。
	\( X \cdot (X + Y) = X \)
对偶律	\( X \cdot 0 = 0 \) 与 \( X + 1 = 1 \)	AND 和 OR 运算的对偶表达，适用于布尔表达的简化。

通过这些定律，可以简化和优化数字逻辑电路的布尔表达式，减少冗余逻辑，提升设计效率。

消去律可以通过分配律等其他布尔代数定律推导出来。让我们通过推导过程来看一下消去律的推导。

消去律推导过程

消去律的表达式为：

\[ x + x’y = x + y \]

这个表达式其实是通过分配律和一些其他基本定律推导出来的。以下是推导步骤：

1. 原表达式： \[ x + x’y \]

2. 使用分配律： \[ x + x’y = (x + x’) \cdot (x + y) \]

3. 应用补元律：根据 \( x + x’ = 1 \)，我们可以进一步简化这个表达式。 \[ (x + x’) \cdot (x + y) = 1 \cdot (x + y) \]

4. 应用单位元律：根据 \( 1 \cdot A = A \)，我们得到最终结果： \[ x + y \]

这样就推导出了消去律：\( x + x’y = x + y \)。

Canonical Forms

1. 积之和形式（Sum of Products, SOP）

2. 和之积形式（Product of Sums, POS）

• 也称为合取范式（Conjunctive Normal Form, CNF）或最大项扩展（Maxterm Expansion）。POS 表达式由 OR 项组成，每一个最大项表示真值表中输出为 0 的输入组合。
• 最大项（Maxterm）：通过 OR 运算结合所有输入变量，当所有输入组合结果为 0 时，最大项的输出为真。
• POS 是输出为 0 的所有最大项的乘积（AND 操作），是输出为假（False）的条件。
• 可以通过对 SOP 形式应用 德摩根定律（DeMorgan’s Law） 将 SOP 转换为 POS，反之亦然。
• 例子：对于 \( f’ = (a + b + c’)(a + b’ + c)(a’ + b + c) \)，每一项代表输出为 0 的组合。

例子：

从真值表推导出的积之和和和之积形式如下：

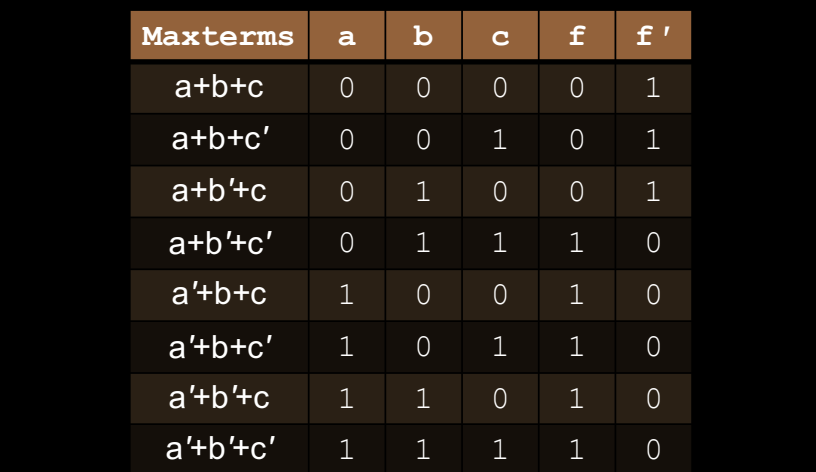
对于输出为 0 的行，POS 形式为： \[ f = (a+b+c)(a+b+c’)(a+b’+c) \]

\[ f’ = (a+b’+c’)(a’+b+c)(a’+b+c’) (a’+b’+c)(a+b+c’) \]

Summary

组合逻辑（Combinational Circuits）

• 输出仅取决于当前输入的值（无记忆性）。
• 组合电路的功能规格可以通过以下两种方式表达：
  • 真值表：列出所有输入组合及对应的输出。
  • 布尔表达式：用逻辑代数符号表示输入与输出之间的关系。

布尔代数（Boolean Algebra）

• 布尔代数处理的是值为 真（True） 或 假（False） 的变量。
• 它自然地映射到硬件逻辑门（如 AND、OR、NOT 等）的实现。
• 通过布尔代数定理（如分配律、结合律等）和 卡诺图（Karnaugh Maps） 来简化复杂的逻辑表达式。