L09-Sequential Circuits
MIT 6.004 2019 L09 Sequential Circuits,由Silvina Hanono Wachman讲述。
这次讲座的主题为:时序电路。
主要内容
- 时序电路与组合电路的区别:
- 时序电路具有状态,可以存储信息,而组合电路则不包含状态存储元素,输出完全取决于当前输入。
- 时序电路需要考虑信号的传播延迟,而组合电路则不涉及。
- 简单反馈电路示例:
- 通过两个互相连接的非门,可以构建一个能够保持0或1状态的电路。
- 如果将三个非门连接成环,电路会在0和1之间振荡,其频率由门的传播延迟决定。
- D触发器和D锁存器:
- D锁存器可以存储一个位的状态,并可以根据控制信号更改或保持该状态。
- D触发器则是在控制信号的边缘变化时(如从0变到1)改变状态,常用于时序电路设计中。
- 真值表和边缘触发的D触发器:
- 真值表显示了D锁存器和D触发器在不同输入下的行为。
- 边缘触发的D触发器在控制信号的上升沿改变输出,有助于同步状态变化。
- 使用蓝图语言描述时序电路(BlueSpec):
- 使用蓝图语言可以将时序电路抽象为模块,并提供清晰的接口进行交互。
- 可以定义模块的内部状态,以及通过接口方法读取或修改这些状态。
- 蓝图语言中的接口和方法:
- 接口定义了模块可以执行的操作和可以获取的信息。
- 方法可以是读取(value method)、改变状态(action method)或两者兼具(action-value method)。
- 模块化设计:
- 模块化设计允许将复杂电路拆分为更小、更可管理的部分。
- 通过模块接口,外部世界不需要了解模块的内部细节即可与之交互。
- 构建时序电路的例子:
- 以模4计数器为例,介绍了如何使用蓝图语言构建和表示一个简单的时序电路。
- 展示了如何定义模块的接口,以及如何描述内部状态和状态转换。
- 状态机(FSM)的使用:
- 状态机是描述和实现时序电路行为的一种方法。
- 通过定义状态和状态之间的转换来构建复杂的控制流逻辑。
- GCD电路的蓝图实现:
- 介绍了一个计算两个数最大公约数(GCD)的电路的蓝图实现。
- 通过定义模块、规则和内部状态来描述GCD算法的实现。
分页知识点
时序电路
Silvina Hanono Wachman 计算机科学与人工智能实验室 麻省理工学院
组合电路
组合电路不包含周期(反馈)或状态元素。
在计算机硬件中,组合电路是一种不保存任何状态信息的电路类型,电路输出完全取决于当前的输入。在这些电路中,不存在存储过去输入历史的内存元素,因此输出不能被用来影响或改变自身的状态。这一特性使得组合电路的行为更加容易预测和分析。
例如,一个多路选择器(Multiplexer)由多个输入和一个选择信号组成,根据选择信号的不同,输出其中一个特定的输入。一个比较器则可以比较两个输入信号,并根据比较结果输出,比如哪个更大、更小或者相等。算术逻辑单元(ALU)可以执行更复杂的操作,如加法、减法、逻辑运算(AND, OR, XOR等),并可以基于操作结果产生比较信号。
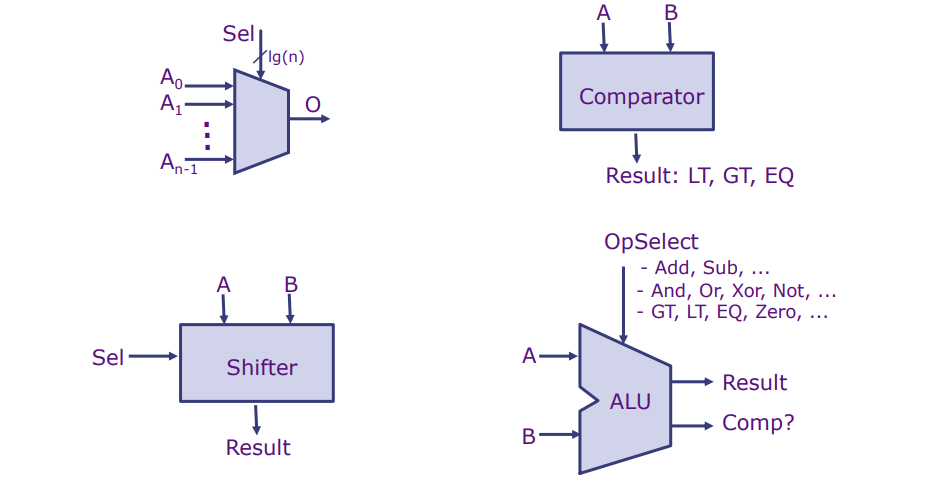
具有反馈的简单电路,即,一个周期
具有周期的电路可以保持状态。
通常,行为难以分析,并且需要关注信号传播延迟。
具有反馈环的电路可以存储信息,这就是我们所说的“具有状态”。例如,图中的第一个反馈电路可以维持一个0或者1的状态,这是通过两个互相连接的逻辑非门实现的。要改变这个电路的状态,我们需要能够干预其运行。
第二个电路展示了一个会在0和1之间振荡的反馈电路。这种振荡的原因是电路内部信号的传播延迟,这会导致输出不稳定,并且在没有外部输入的情况下自发地在两个状态之间切换。
这类带有反馈的电路通常更难以分析,因为它们的行为取决于内部信号的传播时间。在设计时序电路时,工程师必须仔细考虑信号传播延迟,以确保电路可以可靠地在预定的状态之间切换。
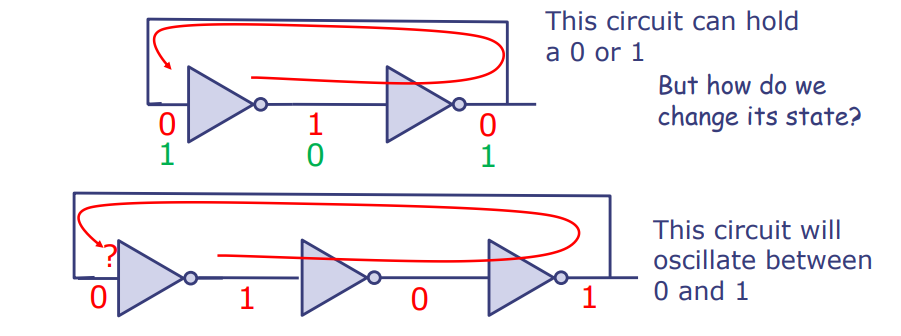
D锁存器:一个著名的可以存储状态的电路
D锁存器通过一个控制信号C来控制数据D是否传递到输出Q。如果C=0,D的值就会传递到Q;如果C=1,则Q的值保持不变。这里的Q代表D锁存器(DL)当前保存的值,Q+1代表下一个状态的值。
真值表解释了D锁存器在不同输入组合下的输出。
以图形化的块图来表示D锁存器,其中黄色块表示锁存器本身,它展示了D输入和C控制信号如何影响Q输出。
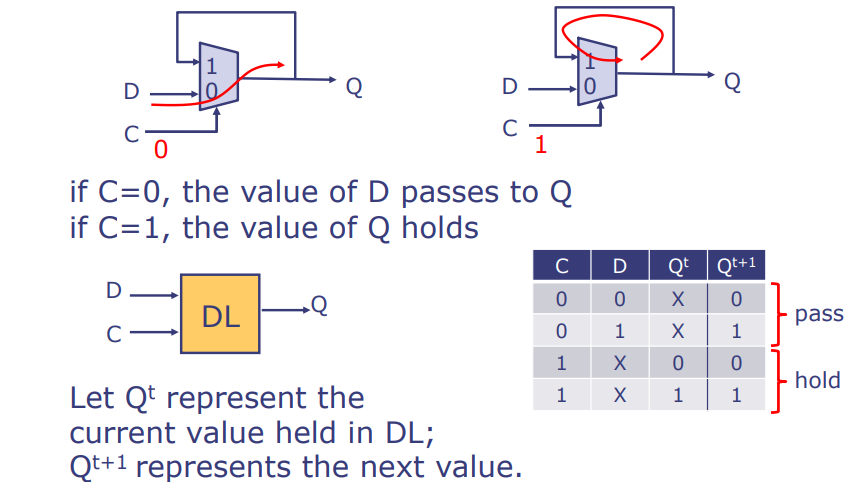
使用D锁存器构建电路
如果两个D锁存器由相同的C信号驱动,它们将在同一时间传递信号以及保持信号。这样的话,由两个D锁存器组成的电路在功能上与单个D锁存器相同(假设信号不会改变得太快)。
在此图中,我们看到了两个D锁存器是如何串联的,其中Q_int代表中间的输出,这也就意味着第一个锁存器的输出会成为第二个锁存器的输入。如果C信号相同,则两者会同时工作。

如果D锁存器由反转的C信号驱动,其中一个始终在“保持”状态,而另一个始终在“传递”状态。这种配置使得电路的行为更加复杂:

- 当C = 0时,Q保持其旧值,但Q_int会跟随输入D。
- 当C = 1时,Q_int保持其旧值,但Q跟随Q_int。
- Q的输出不会在C = 0或C = 1时改变,但是当C从0变到1(C的上升沿)时,Q会改变它的值。
这种配置通常被称为边缘触发电路,它可以在控制信号的特定变化(如上升沿或下降沿)时改变输出状态,非常适用于需要精确同步信号的场合。
在上面的示例中,一个D锁存器接一个反向器,再接一个D锁存器,构成了一个边缘触发电路。这样的设计保证了电路只在C信号的特定变化时更新状态,增强了电路的可预测性和稳定性。
边缘触发D触发器
一种基本的存储元件
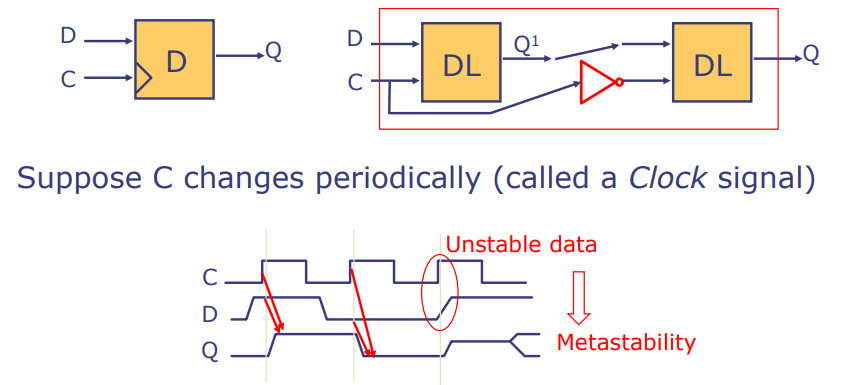
边缘触发D触发器是一种仅在输入C(时钟信号)的上升沿或下降沿变化时改变其输出状态的触发器。假设C信号周期性变化(称为时钟信号),数据在时钟的上升沿被采样,并且必须在该时刻稳定。如果数据在时钟信号的上升沿并不稳定,就可能导致触发器输出处于不稳定状态,这种现象称为亚稳态(Metastability)。
具有写使能的D触发器
时序电路的构建块
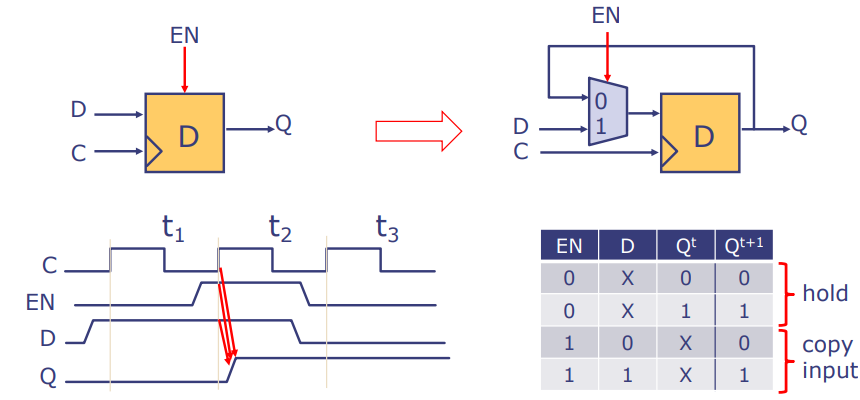
具有写使能(EN)的D触发器允许通过额外的使能信号控制数据是否能被存储到触发器中。只有当EN为高(通常表示为逻辑“1”)时,数据D才会在时钟信号C的下一个上升沿被捕获到输出Q。真值表显示了在使能信号下D输入与Q输出的关系。例如:
- 当EN和D都为0时,无论C如何变化,Q的下一个状态保持不变,因为没有写入操作被使能。
- 当EN为1且D为0时,如果时钟信号C有上升沿变化,Q的下一个状态会更新为0。
图中显示的波形图解释了在不同时间点(t1, t2, t3)的EN、C和D的状态如何影响Q的输出。
注意:在这种类型的触发器中,时钟信号通常是隐含的,并且不需要在电路图中显式表示出来。
寄存器
一组具有共同时钟和使能信号的D触发器
寄存器是一组串联的D触发器,它们共享同一个时钟信号和使能信号。这些串联的D触发器允许存储多位的数字,通常用于计算机内存中的寄存器实现。
寄存器文件则是一组这样的寄存器,它们有共同的时钟,以及共享的输入输出端口,使得可以同时对多个寄存器进行读写操作。这在中央处理单元(CPU)中非常重要,因为它允许快速访问和更新存储在其中的数据。

时钟序列电路
- 在本课程中,我们只讨论有时钟的序列电路。
- 我们还将假设所有的触发器都连接到相同的时钟上。
- 为了避免图表杂乱,时钟输入将被隐含,不在图中显示。
- 在BSV描述中,只有在设计多时钟电路时,才需要指明时钟输入。
这意味着在设计和理解时钟序列电路时,我们可以假定时钟信号是隐式存在的,而无需在每个元件或者电路图中明确指出。这样可以简化电路图的设计,因为所有的触发器都是同步工作的,节省了绘制和解释电路时的工作量。在使用硬件描述语言如BSV来描述这些电路时,同样适用这样的规则,除非需要处理复杂的多时钟问题。
一个例子:模4计数器
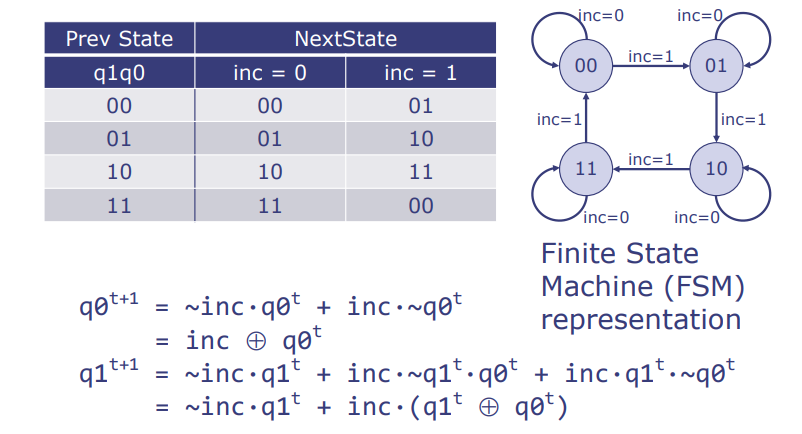
模4计数器是一个简单的状态机,它在每个时钟脉冲上增加其计数值,并在达到特定值(在这个例子中是4)后回到0重新开始计数。以下是其状态转换:
- Prev State(前一状态) 与 NextState(下一状态) 之间的真值表,显示了在增量信号
inc为0和1时,计数器状态如何变化。- 当
inc为0时,状态保持不变。 - 当
inc为1时,状态按照模4递增。
- 当
以下是该计数器状态转换的布尔代数表达式:
q0_t+1 = ~inc · q0_t + inc · ~q0_t- 可以简化为
q0_t+1 = inc ⊕ q0_t
- 可以简化为
q1_t+1 = ~inc · q1_t + inc · ~q1_t · q0_t + inc · q1_t · ~q0_t- 可以简化为
q1_t+1 = ~inc · q1_t + inc · (q1_t ⊕ q0_t)
- 可以简化为
最后,使用有限状态机(FSM)图表表示,可以直观地展示状态之间是如何转换的,这是理解和设计数字电路中常用的方法。
在FSM的图示中,每个状态用一个圆圈表示,状态之间的转换用带箭头的线表示,并标注了使状态转换发生的条件(例如 inc=0 或 inc=1)。这种图形化的表示方法有助于快速识别电路的行为和可能的状态路径,是设计和验证复杂电路时的重要工具。
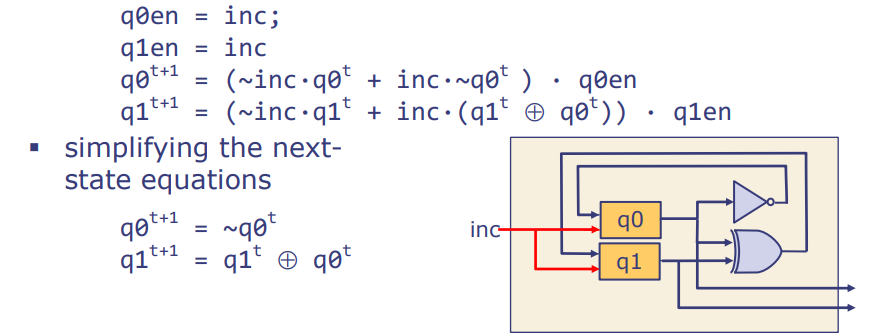
模4计数器电路使用具有使能的D触发器
- 利用两个具有使能功能的D触发器来存储q0和q1。
- 注意,只有当使能信号为真时,触发器的状态才会改变。因此,触发器的下一状态输入仅在其使能为真时才有意义。
q0en = inc; q1en = inc;表示使能信号是由增量信号inc控制的。- 状态转换方程经过简化后得到:
q0_t+1 = ~q0_tq1_t+1 = q1_t ⊕ q0_t
电路图展示了这两个D触发器如何通过逻辑门相连并被同一增量信号 inc 控制,以实现状态的递增。
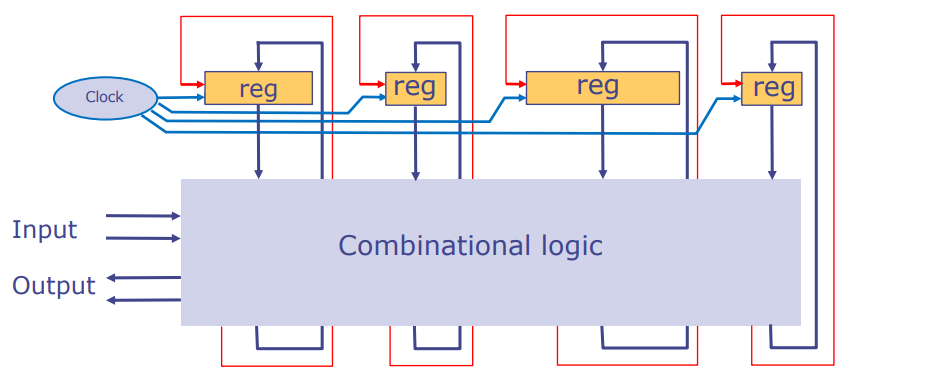
同步序列电路使用寄存器
这一部分展示了如何使用寄存器和组合逻辑构建同步序列电路。在设计中,所有寄存器都连接到相同的时钟输入,因此未来我们在电路图中不会画出时钟线。
图示的电路结构包含多个寄存器,它们通过一组组合逻辑进行交互,以实现更复杂的功能。每个寄存器通过时钟信号同步,确保电路整体的动作是协调一致的。组合逻辑负责处理输入信号,并根据这些信号以及寄存器的当前状态来决定寄存器的下一个状态,这些新状态在下一个时钟周期被捕获。
这样的电路设计方法有助于设计稳定且可预测的数字系统,因为所有的状态变化都是在同一个时钟信号的同步下发生的,降低了不同部分之间的时序问题。在这种设计中,输入信号通过组合逻辑产生对寄存器的控制信号,同时也可能直接影响输出信号,实现快速的电路响应。
有限状态机 (FSMs)
- 同步序列电路是实现硬件FSM的一种方法。
- FSM是一个被广泛研究的数学对象,类似于布尔代数。
- FSM在软件中也得到了广泛应用。
- 事实上,任何数字硬件(包括计算机)都可以被视为FSM,尽管我们通常不这样考虑。
有限状态机(FSM)是描述数字电路特定部分行为的一种模型。它由一组状态、输入信号、输出信号和根据当前状态和输入信号确定下一个状态的转移函数组成。在硬件设计中,FSM使我们能够精确地描述和实现复杂逻辑的操作序列。
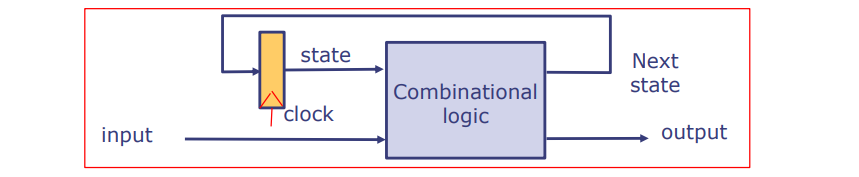
作为具有接口的模块的序列电路
- 模块具有内部状态和一个接口。
- 内部状态只能通过其接口方法读取和操作。
- 一个动作(action)方法指定了哪些状态元素将被修改;它有一个使能(enable)线,使能必须为真才能执行动作。
- 动作是原子性的——要么指定的所有状态元素都被修改,要么都不修改(不可见部分修改状态)。
- 我们将模块的接口视为其类型。
在这里,”模块”是指一个可以封装内部状态和行为的组件。在BSV(蓝图语言)中,模块的概念类似于Java或C++中的类定义。例如,一个计数器模块可以有增加(inc)和读取(read)的方法,以及一个内部的状态表示当前计数。
接口定义了可以对模块执行哪些操作,以及可以从模块获取哪些信息。例如,在上图中的计数器接口中定义了两个方法:inc 用于增加计数器的值,read 用于返回计数器的当前值。这使得与模块的交互被明确地限定在一组预定义的操作内,提高了设计的可维护性和模块性。

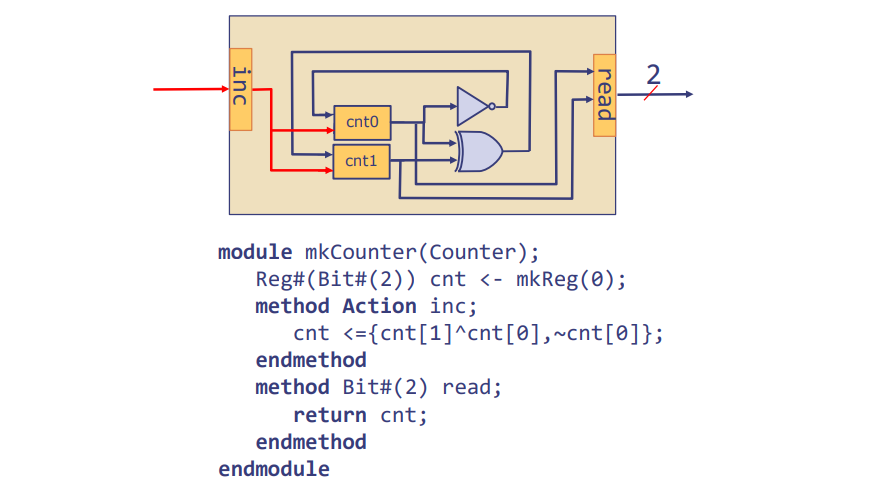
模4计数器:Bluespec中的实现
-
接口定义
interface Counter; method Action inc; method Bit#(2) read; endinterface
在Bluespec中,Counter 接口定义了一个模块,这个模块有两个方法:inc 用来增加计数器的值,read 用来读取当前的计数器值。这里的 Bit#(2) 表示返回值是一个2位的二进制数。
-
模块实例化
module mkCounter(Counter); Reg#(Bit#(2)) cnt <- mkReg(0);
mkCounter 模块实现了 Counter 接口。它定义了一个2位宽度的寄存器 cnt,并使用 mkReg(0) 初始化为0。这里的 Reg#(Bit#(2)) 是Bluespec语法,表示创建一个2位的寄存器。
-
状态指定与初值
method Action inc; cnt <= {cnt[1] ^ cnt[0], ~cnt[0]}; endmethod
inc 方法是一个动作(Action),当调用时会更新 cnt 寄存器的值。这里的 {cnt[1] ^ cnt[0], ~cnt[0]} 是更新计数器的逻辑,其中 ^ 表示位异或运算,~ 表示位非运算。这个逻辑表示当 inc 被调用时,cnt 的最低位将翻转,高位将根据最低位和自己当前的值进行异或运算,这就实现了模4的计数。
-
读取方法
method Bit#(2) read; return cnt; endmethod
read 方法返回当前 cnt 的值,使得外部可以查询计数器的当前状态。
-
结束模块
endmodule
这表示 mkCounter 模块定义的结束。
模块的设计使得 inc 和 read 方法提供了操作和查询计数器状态的机制,同时隐藏了内部的实现细节。这样的模块化设计方便了电路的重用和维护,同时也使得电路的测试和验证更加简单。
在下方的电路图中,我们可以看到这个模块被翻译成了实际的硬件,其中包含逻辑门和D触发器,这些都是由Bluespec代码自动生成的。这表明了使用高级硬件描述语言(如Bluespec)可以直接从概念性描述中生成硬件设计,提高了设计的效率和准确性。
总结
- 时序电路具有状态,并通过使用寄存器来存储状态。
- 寄存器具有使能信号,只有在使能信号为真时,它的状态才能被改变。
- 时序电路在Bluespec中由模块表示,并具有一组明确的接口方法来读取和修改其状态。
- 在Bluespec中,寄存器是一种原始模块类型。
- 模块可以被多次实例化,创建同类型的对象,即时序电路。
时序电路是数字逻辑设计的基础,允许电路在不同时间点根据输入信号和内部状态做出响应。在Bluespec这类硬件描述语言中,可以通过定义模块和其接口来清晰地封装电路的功能和状态,这使得设计可以模块化,易于理解、测试和重用。
带回家的问题
- 编写一个模块,可以增加、减少或不改变计数器的值。
- 这个模块需要一个忙碌的方法吗?
这些问题鼓励学生思考如何在硬件描述语言中实现计数器的基本功能,以及在设计时考虑模块的状态管理。”忙碌”方法可能涉及检查模块是否在执行长时间运行的操作,这是在某些应用中保持系统同步的重要特性。
计算GCD的方法
- 欧几里得算法用于计算最大公约数(GCD):
- 例如,求15和6的最大公约数时,可以不断交替从较大数中减去较小数,直到其中一个数减至0。最终非零数即为两数的最大公约数。
这部分以Python伪代码展示了欧几里得算法的实现:
def gcd(a, b):
if a == 0: return b # 如果a为0,则b为最大公约数
elif a > b: return gcd(a-b, b) # 如果a大于b,a减去b
else: return gcd(b, a) # 否则交换a和b的值
这个算法例子展示了递归函数的一个实例,其中每次函数调用都会使问题规模缩小,直到达到终止条件。类似的算法可以在硬件设计中实现,用于在数字电路中计算GCD。
GCD模块
- GCD模块可以在不忙碌时开始计算。
- 结果可以在准备好时读取。
interface GCD;
method Action start(Bit#(32) a, Bit#(32) b);
method ActionValue#(Bit#(32)) getResult;
method Bool busy;
method Bool ready;
endinterface
在Bluespec中定义了一个GCD接口,它包含四个方法:start 用来初始化GCD计算,接收两个32位的输入 a 和 b;getResult 返回计算结果,并结束当前操作;busy 返回模块是否忙碌;ready 表明结果是否准备好读取。
BSV中的GCD
module mkGCD (GCD);
Reg#(Bit#(32)) x <- mkReg(0);
Reg#(Bit#(32)) y <- mkReg(0);
Reg#(Bool) busy_flag <- mkReg(False);
rule gcd;
if (x >= y) begin x = x - y; end // subtract
else if (x != 0) begin x = y; y = x; end // swap
endrule
method Action start(Bit#(32) a, Bit#(32) b);
x = a; y = b; busy_flag = True;
endmethod
method ActionValue#(Bit#(32)) getResult;
busy_flag = False; return y;
endmethod
method Bool busy = busy_flag;
method Bool ready = x==0;
endmodule
在这个Bluespec代码片段中,mkGCD 模块实现了GCD接口。模块内部包含了两个32位的寄存器 x 和 y 用于存储GCD的输入值,以及一个布尔寄存器 busy_flag 用于指示模块是否正在计算。
gcd规则定义了GCD算法的主体,当x不为0并且大于等于y时,x减去y;当x不为0但小于y时,交换x和y。start方法初始化GCD计算,存储输入到x和y,并将忙碌标志设置为真。getResult方法结束GCD计算,将忙碌标志设置为假,并返回计算结果。busy方法返回忙碌标志的当前值。ready方法检查x是否为0,如果为0,表示计算已完成,结果准备好读取。- 仅当模块不忙时才应调用
start;仅当ready为true时才应调用getResult
这个模块的设计表明,GCD计算可以作为独立的操作进行,不干扰其他电路部分的工作。Bluespec语言提供了一种高层次的方式来描述这种行为,使得硬件设计更加接近于软件设计。这种模块化的方法能够简化并行计算和状态管理,特别是在复杂的数字系统中。
规则
- 模块可能包含规则。
规则是一个行动的集合,这些行动调用方法。规则中的所有行动都并行执行。规则可以在任何时候执行,而且当它执行时,它的所有行动都必须执行,这就是原子性。
例如,下面的BSV代码定义了一个名为 gcd 的规则:
rule gcd;
if (x >= y) begin
x <= x - y; // subtract
end else if (x != 0) begin
x <= y; y <= x; // swap
end
endrule
- 这个规则描述了GCD(最大公约数)算法的两个基本操作:如果
x大于等于y,则x减去y;如果x不等于0且小于y,则交换x和y的值。
动作和双重写入的并行组合
在BSV中,如果一个规则包含可能导致对同一个变量进行多次写入的行动,那么这样的并行组合是非法的,BSV编译器会拒绝这样的程序。
例如,以下是一些包含双重写入潜在问题的规则:
rule one;
y <= 3; x <= 5; x <= 7; // Double write to x
endrule
rule two;
y <= 3; if (b) x <= 7; else x <= 5; // No double write
endrule
rule three;
y <= 3; x <= 5; if (b) x <= 7; // Possibility of a double write
endrule
- 在规则
one中,变量x被分配了两次,这是非法的,并且会导致编译错误。 - 在规则
two中,尽管x有两个潜在的赋值,但由于它们在条件语句中,所以在任何执行路径上x只会被赋值一次,这是合法的。 - 在规则
three中,存在x被分配两次的可能性,因为它依赖于条件b,这也是非法的。
在BSV编程中,规则的设计必须确保不会违反这些约束,以避免竞争条件和不确定的行为。这些规则确保了在BSV设计的硬件中,所有的行动都是原子执行的,要么全部执行,要么全部不执行,这有助于保持硬件行为的一致性和可预测性。