Lecture 6: Floating Point

Review of Integer Number Representations

整数表示法回顾

计算机通过位（bits）来处理和表示数字。

在N位中可以表示多少种数值？
- 一共有 \(2^N\) 种不同的组合，这些组合可以用来表示不同的数值。让我们回顾一些常见的数值表示方法。

无符号整数（Unsigned integers）

范围：0 到 \(2^N - 1\)
- 例如，当 \(N = 32\) 时：
  - 无符号整数的范围是 0 到 \(2^{32} - 1\)，即 0 到 4,294,967,295。

有符号整数（Signed Integers，二进制补码表示）

范围：\(-2^{N-1}\) 到 \(2^{N-1} - 1\)
- 例如，当 \(N = 32\) 时：
  - 有符号整数的范围是 \(-2^{31}\) 到 \(2^{31} - 1\)，即 -2,147,483,648 到 2,147,483,647。

What about other numbers?

其他数字呢？

非常大的数字（如每千年的秒数）

31,556,926,010（科学记数法表示为 \(3.155692610 \times 10^{10}\)）

非常小的数字（如玻尔半径）

0.000000000052917710（科学记数法表示为 \(5.2917710 \times 10^{-11}\)）

同时包含整数和小数部分的数字

例如 2.625。

“Fixed Point” Binary Representation

“定点”二进制表示法

“二进制点”（Binary Point） 类似于小数点，用于区分整数部分和小数部分。

6位表示法示例，仅正数：

101010 表示为 1 0 . 1 0 1 0
- 计算方式：\(1 \times 2^1 + 0 \times 2^0 + 1 \times 2^{-1} + 0 \times 2^{-2} + 1 \times 2^{-3} + 0 \times 2^{-4}\)
- 即：\(2 + 0.5 + 0.125 = 2.625\)

使用上述6位“固定二进制点”表示法的范围：

范围：0 到 3.9375
- 计算方式：\(11.111_2 = 3.9375\)，即 \( 4 - 2^{-4} \)

Arithmetic with Fixed Point

定点数的算术运算

加法是直接的：

例如，计算 (1.1000 + 1.0100)
- 结果为：(2.1100)

乘法稍微复杂一些：

例如，计算 \(1.1000 \times 0.0100\)
- 结果为：\(0.1100\)

需要记住二进制点的位置：

在进行定点数运算时，必须记住并正确处理二进制点的位置，以确保结果的正确性。

What about other numbers?

31,556,926,010（科学记数法表示为 \(3.155692610 \times 10^{10}\)）
0.000000000052917710（科学记数法表示为 \(5.2917710 \times 10^{-11}\)）

存储所有这些数字需要更高的精度和更大的位数：

使用定点表示法存储上述所有类型的数字至少需要 92 位的精度，这显然是不切实际的。必须有更好的方法来表示这些数字，这就引出了浮点数表示法。
通过理解整数和定点数的表示及运算，可以更好地掌握计算机如何处理数值数据，但对于处理范围更广、精度更高的数值数据，需要学习浮点数表示法。

Floating Point

浮点数

“浮动二进制点”（floating binary point） 是一种有效利用有限位数的方法，提高了数字表示的准确性和范围。

示例：

假设我们要表示 0.1640625₁₀。
二进制表示：… 000000.001010100000…
1. 存储这些“有效位”（significant bits）。
2. 记录最高有效位（MSB）左侧 2 位的二进制小数点（“指数字段”）。

二进制点 独立于有效位存储，因此可以表示非常大和非常小的数字。通过分离有效位和指数，我们可以动态调整二进制点的位置，从而扩展表示范围。

Enter Scientific Notation (in Decimal)

使用科学计数法（十进制）

“规范化形式”（Normalized form）：确保小数点左边只有一个非零数字，这样可以最大化表示的精度。

要表示 3 / 1,000,000,000：
- 规范化：3.0 x 10^-9
- 非规范化：0.3 x 10^-8 或 30.0 x 10^-10

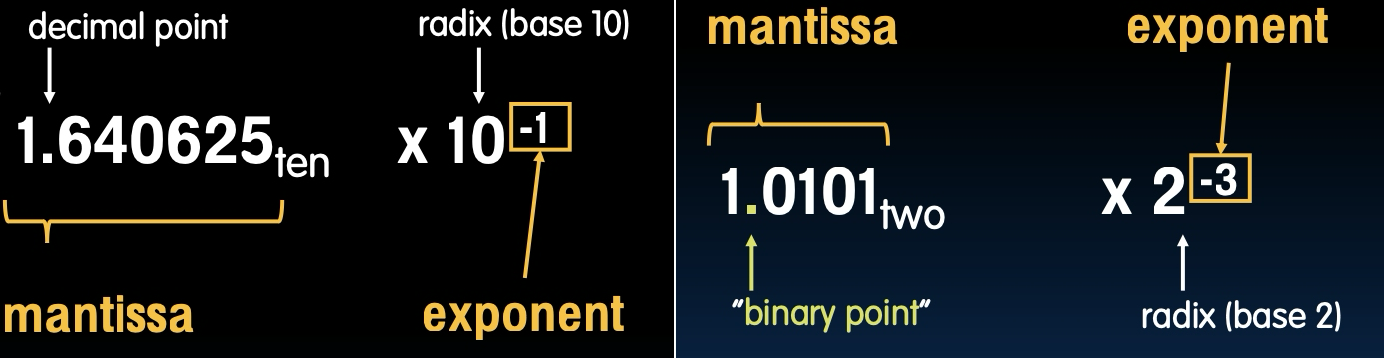
表示 1.640625₁₀ x 10^-1

基数（底数）：x 10⁰
尾数（mantissa）：1.640625
指数（exponent）：-1

Enter Scientific Notation (in Binary)

使用科学计数法（二进制）

“浮点数”（Floating point）

浮点数表示法允许二进制点的位置不固定，从而表示范围更广的数字。
C语言变量类型：float，double

表示 1.0101₂ x 2^-3

基数（底数）：x 2⁰
尾数（mantissa）：1.0101₂
指数（exponent）：x 2^-3

注意：规范化二进制表示总是以1开头！

这是因为在二进制表示中，除0之外的所有数字都可以表示为1.xxx…，这确保了尾数的最高有效位总是1，从而最大化表示的精度。

IEEE 754 Floating Point Standard

IEEE 754 浮点标准

单精度标准用于 32 位字。在 C 语言中表示为 float。

规范化形式：

±1.xxx…x_two × 2^YYY…Y_two

字段说明：

符号位（Sign bit，s）
- 1 表示负数
- 0 表示正数
指数字段（Exponent field，8 bits）
- 用偏移表示法（bias notation）：
  - 偏移值为127：从指数字段减去127以获得实际指数值。
  - 这种设计使得浮点数可以方便地使用整数比较来排序，即使没有专用的浮点硬件也能进行运算。
  - 对于相同符号的数，更大的指数字段表示更大的数。
  - 通过这种方式，数字按符号-数量的顺序排列：从 00…00 到 11…11，表示从 0 到 +最大值，再到 -0 到 -最大值。
有效数字字段（Significand field，23 bits）
- 为了提高表示精度，尾数前导隐含1：
  - 尾数 = 1 + 23 位有效数字字段
  - 0 < 有效数字字段 < 1

浮点数表示形式：

(-1)^s × (1 + significand) × 2^{(exponent-127)}

详细解释

符号位（Sign bit，s）：

这个位用来表示浮点数的符号。1 表示负数，0 表示正数。
- 实例：
  - 如果符号位是1，例如浮点数的表示是 1xxx xxxx xxxx xxxx xxxx xxxx xxxx xxxx，那么这个数是负数。
  - 如果符号位是0，例如浮点数的表示是 0xxx xxxx xxxx xxxx xxxx xxxx xxxx xxxx，那么这个数是正数。

指数字段（Exponent field，8 bits）：

浮点数的指数部分使用偏移表示法（bias notation），偏移值为127。这意味着存储在指数字段中的实际值减去127后得到实际的指数值。
- 偏移表示法的详细解释：
  - 偏移值（bias）为127，指数字段的实际存储值范围是0到255。
  - 通过偏移127，可以表示-127到128范围内的指数。
  - 例如，存储在指数字段的值为130，那么实际的指数值为 130 - 127 = 3。
  - 如果存储在指数字段的值为100，那么实际的指数值为 100 - 127 = -27。
- 好处：
  - 偏移表示法使指数字段可以表示正数和负数的指数，且避免了处理负数时的复杂性。
  - 指数字段使用无符号整数存储，这使得比较浮点数时可以直接比较存储的二进制数值，而无需额外处理正负号。
- 实例：
  - 对于一个浮点数，指数字段的二进制表示为10000011，其十进制值为131，实际指数值为 131 - 127 = 4。
  - 对于一个浮点数，指数字段的二进制表示为01111110，其十进制值为126，实际指数值为 126 - 127 = -1。

有效数字字段（Significand field，23 bits）：

有效数字字段存储的是尾数的小数部分，但规范化形式的浮点数总是以1开头，所以1是隐含的。
- 这使得23位的有效数字字段实际上表示24位的精度。
- 规范化形式：
  - 规范化的浮点数形式总是以 1.xxx... 表示，因此隐含的1不需要存储。
  - 有效数字字段实际上表示 0.xxx...，然后加上隐含的1。
- 实例：
  - 如果有效数字字段为 10101010101010101010101，其实际尾数为 1.10101010101010101010101。
  - 如果有效数字字段为 00000000000000000000000，其实际尾数为 1.00000000000000000000000。

浮点数表示形式：

结合符号位、指数字段和有效数字字段，浮点数的实际值可以表示为：(-1)^s × (1 + significand) × 2^{(exponent-127)}
- 这里，s是符号位，significand是有效数字字段的值，exponent是指数字段的值。
- 实例：
  - 例如，浮点数的二进制表示为 0 10000011 10100000000000000000000：
    - 符号位 s = 0，表示正数。
    - 指数字段 10000011，其十进制值为131，实际指数值为 131 - 127 = 4。
    - 有效数字字段 10100000000000000000000，实际尾数为 1.101。
    - 组合得到的浮点数实际值为 1.101 × 2^4 = 1.625 × 16 = 26.0。
  - 例如，浮点数的二进制表示为 1 01111110 01000000000000000000000：
    - 符号位 s = 1，表示负数。
    - 指数字段 01111110，其十进制值为126，实际指数值为 126 - 127 = -1。
    - 有效数字字段 01000000000000000000000，实际尾数为 1.01。
    - 组合得到的浮点数实际值为 -1.01 × 2^-1 = -1.25 × 0.5 = -0.625。

“Father” of the Floating Point Standard

浮点标准的“之父”

IEEE Standard 754 for Binary Floating-Point Arithmetic

IEEE 754 二进制浮点运算标准。

1989 ACM 图灵奖得主：威廉·卡恩教授（Prof. William Kahan）

威廉·卡恩教授被誉为IEEE 754浮点标准的“之父”。他的工作极大地影响了现代计算机科学，特别是在精确和可靠的数值计算领域。

Normalized Example

规范化示例

题目：以下 IEEE 754 单精度二进制浮点数的十进制等价是什么？

1 1000 0011 111 0000 0000 0000 0000 0000

计算步骤：

符号位（Sign bit）： 1（表示负数）
指数字段（Exponent）： 1000 0011（转换为十进制为 131）
- 实际指数 = 131 - 127 = 4
有效数字字段（Significand）： 111 0000 0000 0000 0000 000
- 隐含的1，因此有效数字为 1.111

浮点数表示形式：

\[ (-1)^1 × (1 + .111) × 2^{(131-127)} = -1 × 1.111 × 2^4 = -1 × 1.875 × 16 = -30.0 \]

因此，浮点数 1 1000 0011 111 0000 0000 0000 0000 0000 的十进制等价是 -30.0。

Step Size

步长

题目：Y 之后的下一个可表示的数字是什么？Y 之前呢？

0 1000 0011 111 0000 0000 0000 0000 0000

Y = 0 1000 0011 111 0000 0000 0000 0000 0000

下一个浮点数：

0 1000 0011 111 0000 0000 0000 0000 0001

计算：\[Y + ((.0…01)_2 × 2^{(131-127)}) = Y + (2^{-23} × 2^4) = Y + 2^{-19}\]

由于浮点数有固定数量的位，不能表示所有可能的数字，因此存在步长。
步长是指具有给定指数的连续浮点数之间的间距：
- 指数越大，步长越大。
- 指数越小，步长越小。

Special Numbers

Representing Zero

表示零

注意：零没有规范化表示法（没有前导1）。

IEEE 754 表示 ±0：

保留指数值为 0000 0000，向硬件信号不隐含加1。
保持有效数字字段全为零。
符号位可以为 0 或 1，两种情况都有效。

表示：

+0: 0 0000 0000 000...000
-0: 1 0000 0000 000...000

为什么两种表示都是有效的？

在数值计算中，正零和负零通常被认为是相等的，但在某些情况下，它们可以携带额外的符号信息。IEEE 754标准允许存在正零和负零，以支持这种区分。

Special Numbers

特殊数字

规范化数字只是浮点数表示的一部分。对于单精度浮点数：

偏移指数 (Biased Exponent)	有效数字字段 (Significand Field)	对象 (Object)
0	全为零	±0
0	非零	次正规数
1 - 254	任意	规范化浮点数
255	全为零	±∞
255	非零	NaN

Kahan 教授提出了一个聪明的设计：“不浪费，不缺乏。”即使在表示特殊数字时，也尽量不浪费位的使用。

偏移指数字段0和255用于处理溢出、下溢和算术错误。

Overflow and Underflow

上溢和下溢

由于0和255是保留的指数字段，单精度浮点数的规范化范围是：

最大值：

s 1111 1110 1...1 (23 bits)
(1.1...1) × 2^(254-127) ≈ 3.4 × 10^38

最小值：

s 0000 0001 0...0 (23 bits)
(1.0) × 2^(1-127) ≈ 1.2 × 10^-38

范围示意图：

-3.4×10^38 ---- -1.2×10^-38 ---- 0 ---- 1.2×10^-38 ---- 3.4×10^38

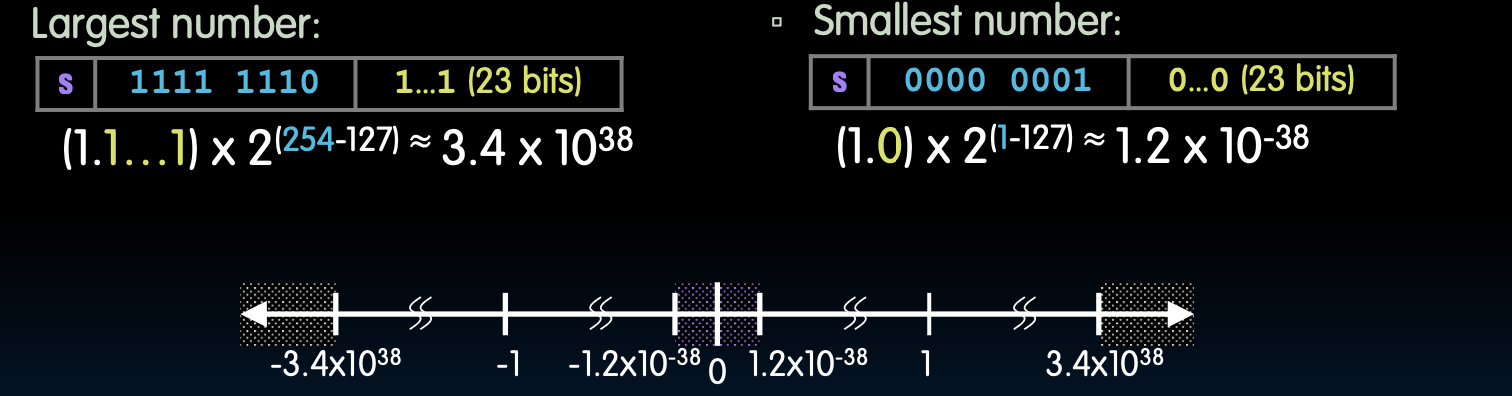
如果数字超出此范围会怎样？

太大：上溢（overflow）。值的大小太大，无法表示，会被表示为±∞。
太小：下溢（underflow）。值的大小太小，无法表示，接近于零。

Representation for ±∞

± ∞ 的表示

在浮点数中，除以±0应产生±∞，而不是上溢。

为什么？

可以使用∞进行进一步计算。例如，X / 0 > Y 可能是有效的比较。
问数学专业的同学，∞在计算中有实际意义。

IEEE 754 表示 ±∞：

保留指数值 1111 1111。
有效数字字段全为零。

表示：

+∞: 0 1111 1111 000...000
-∞: 1 1111 1111 000...000

Representation for Not a Number

非数字 (NaN) 的表示

问题：如果计算 sqrt(-4.0) 或 0/0 会得到什么？

如果 ∞ 不是错误，那么这些也不应该是错误！
称为非数字 (NaN) (Not a Number)。

IEEE 754 表示 NaN：

指数 = 255
有效数字字段非零。

为什么这有用？

NaN 会污染操作：任何与 NaN 参与的计算结果都是 NaN。例如，op(NaN, X) = NaN。
NaN 对调试有帮助：可以用有效数字字段来编码/标识错误发生的位置（专有的，未在标准中定义）。

表示：

s 1111 1111 xxx...xxxxx

实例：
- 计算sqrt(-4.0)，结果是 NaN。
- 计算0/0，结果也是 NaN。
- NaN 可以携带额外的信息，例如调试信息或错误代码，这些信息存储在有效数字字段中。

Denorms: Gradual Underflow (1/2)

非规范化数：渐进下溢 (1/2)

问题：

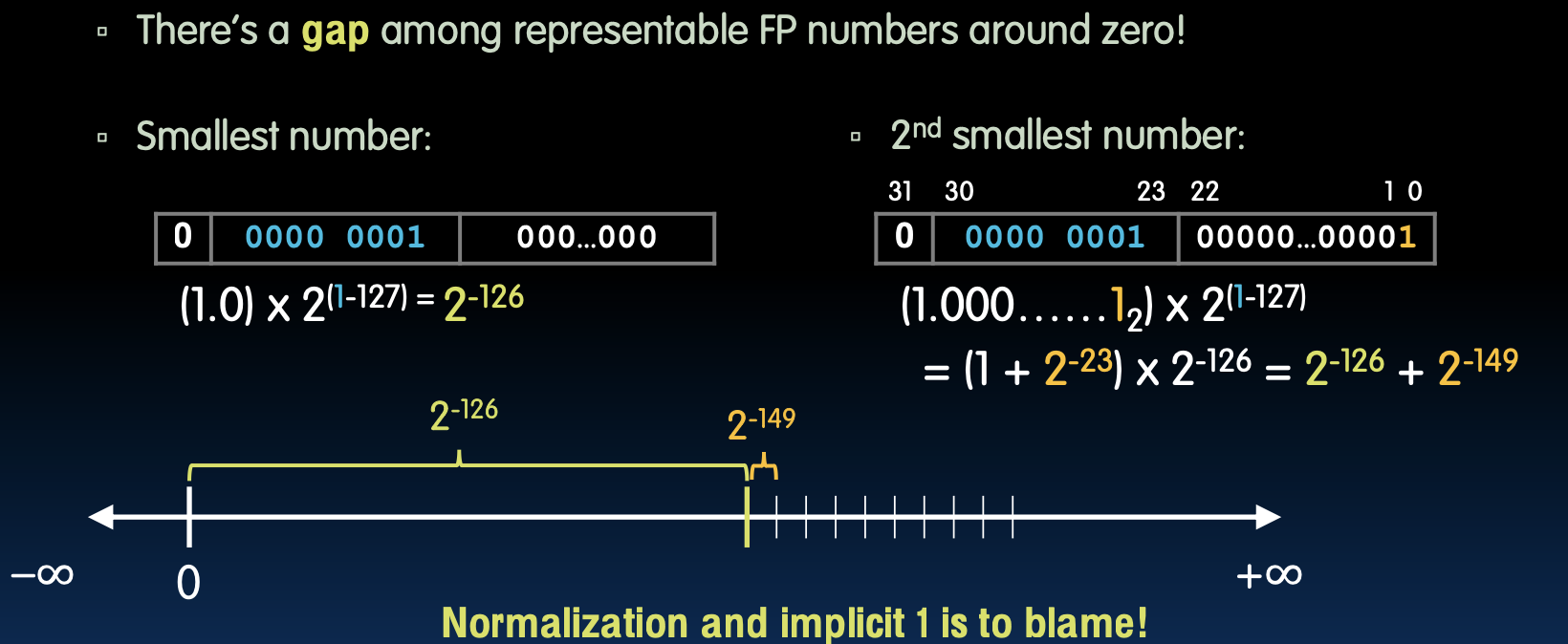
零附近的可表示浮点数之间存在一个间隙。这会导致数值计算中的精度损失。

最小的规范化数字：

0 0000 0001 000...000
(1.0) × 2^(1-127) = 2^-126

第二小的规范化数字：

0 0000 0001 000...0001
(1.000...001_2) × 2^(1-127)
= (1 + 2^-23) × 2^-126
= 2^-126 + 2^-149

由于使用了归一化形式和隐含的1，在零附近的表示间隔较大，导致数值精度不足。

Denorms: Gradual Underflow (2/2)

非规范化数：渐进下溢 (2/2)

解决方案：

我们可以使用指数为0，有效数字非零的表示来解决此问题。
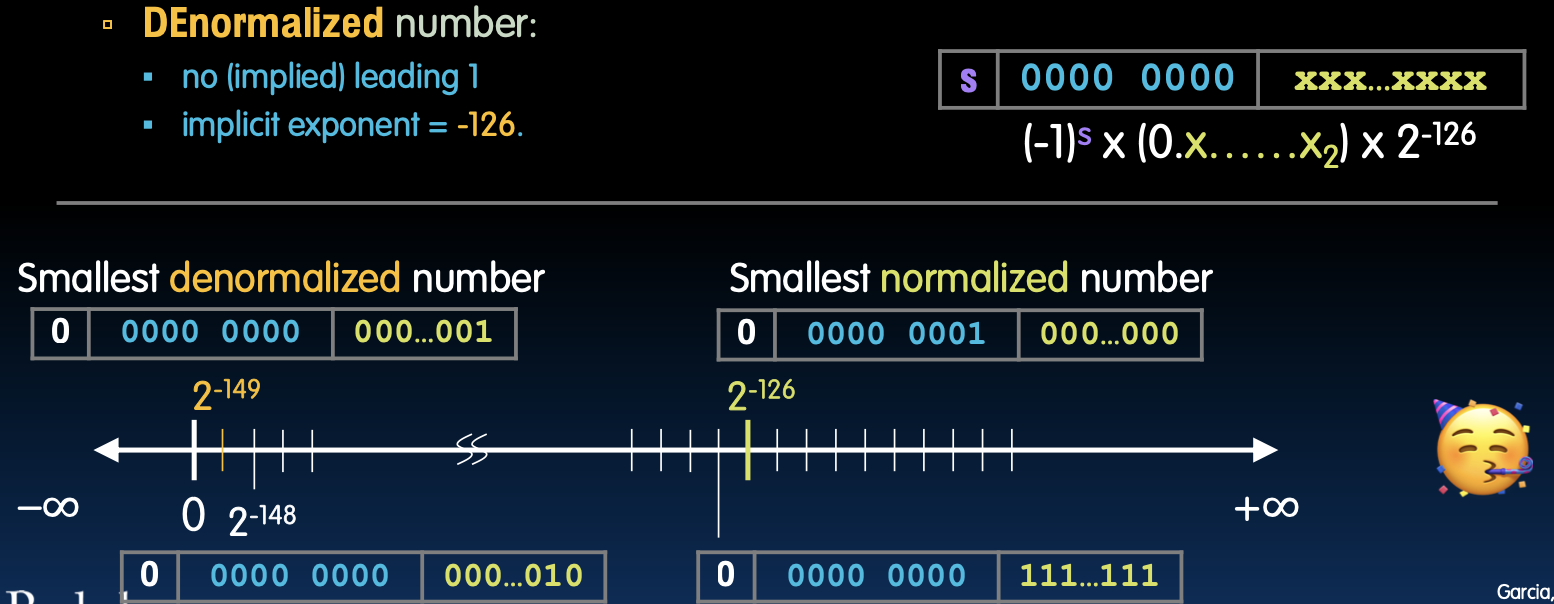
非规范化数：
- 没有隐含的前导1
- 隐含指数为 -126

表示：

s 0000 0000 xxx...xxxxx
(-1)^s × (0.xxx...x_2) × 2^-126

最小的非规范化数和最小的规范化数：

最小的非规范化数：
0 0000 0000 000...0001
2^-149

最小的规范化数：
0 0000 0001 000...0000
2^-126

非规范化数允许表示更接近零的数值，提供了更高的精度，避免了在接近零时出现的数值间隙。

规范化数与非规范化数的设计逻辑

规范化浮点数

规范化浮点数的设计是为了最大化表示范围和精度。这些数总是以隐含的1开头，这意味着尾数总是形式为 1.xxx…。这种表示法确保了在有限的位数内最大化存储的有效信息。

隐含的1：为了节省空间，不存储这个1，而是默认存在。

有效数字（Significand）：存储的是小数部分 xxx…。

由于有隐含的1，所以规范化数不能表示零或非常接近于零的数。

规范化数的示例

最小的规范化数：

二进制表示：0 0000 0001 000...0000

指数部分：1 （实际值为 1 - 127 = -126）

尾数部分：隐含1加上全零，即 1.0

实际值： (1.0 \times 2^{-126} = 2^{-126})

非规范化浮点数

为了能够表示零和非常接近于零的数，引入了非规范化浮点数。这些数不使用隐含的1，而是允许尾数为 0.xxx…。

没有隐含的1：这意味着尾数可以是 0.xxx…。

指数部分为0：但在计算时实际指数值为 -126（为了保持一致性）。

非规范化数的示例

最小的非规范化数：

二进制表示：0 0000 0000 000...0001

指数部分：0 （实际值为 0 - 127 = -127）

尾数部分：0.000…0001 （没有隐含的1）

实际值： (0.000…0001 \times 2^{-126} = 2^{-149})

表示零：

二进制表示：0 0000 0000 000...0000

指数部分：0

尾数部分：0.0

实际值：0

重要性

非规范化数的引入：

填补间隙：解决了规范化数在零附近无法表示非常小数值的问题。

渐进下溢：提供了一种更平滑的下溢方式，使得在接近零时计算结果更精确。

示例总结

最小的规范化数：0 0000 0001 000...0000 表示 (2^{-126})

最小的非规范化数：0 0000 0000 000...0001 表示 (2^{-149})

零：0 0000 0000 000...0000 或 1 0000 0000 000...0000

通过这样的设计，IEEE 754标准能够更全面地表示从非常大的数到非常小的数，包括零，从而增强了数值计算的范围和精度。

Special Numbers, Summary

特殊数字，总结

偏移指数 (Biased Exponent)	有效数字字段 (Significand Field)	对象 (Object)
0	全为零	±0
0	非零	非规范化数
1 - 254	任意	规范化浮点数
255	全为零	±∞
255	非零	NaNs

偏移指数字段0和255用于处理溢出、下溢和算术错误。

±0：当指数为0且有效数字字段全为零时，表示+0或-0。
非规范化数：当指数为0且有效数字字段非零时，用于表示非常接近于零的小数。
规范化浮点数：当指数在1到254之间时，表示规范化浮点数。
±∞：当指数为255且有效数字字段全为零时，表示正无穷或负无穷。
NaNs：当指数为255且有效数字字段非零时，表示非数字（NaN）。

Other Floating Point Representations

其他浮点数表示

Precision and Accuracy

精度和准确性

不要混淆这两个术语！

精度（Precision）：表示一个值所用位数的计数。更多的位数意味着更高的精度。
准确性（Accuracy）：表示一个值的实际值与其计算机表示之间的差异。准确性取决于计算机表示值与真实值的接近程度。

高精度允许高准确性，但不保证高准确性。

有可能具有高精度但低准确性。
示例：
```
float pi = 3.14;
```
- pi 将使用所有23位有效数字表示（高精度），但它只是一个近似值（不准确）。

Double Precision Floating Point

双精度浮点数

binary64：64位

字段说明：
- 符号位（Sign bit）：1位
- 指数（Exponent）：11位
- 有效数字（Significand）：52位

双精度（vs. 单精度）

C 变量声明为 double
指数偏移现在为1023。
表示范围约为 \(2.0 \times 10^{-308}\) 到 \(2.0 \times 10^{308}\)。
主要优势是由于更大的有效数字带来的更高准确性。

Other Floating Point Representations

其他浮点数表示

四倍精度（Quad-Precision）：128位，称为“binary128”
- 难以置信的范围和精度
- 15位指数，112位有效数字
八倍精度（Oct-Precision）：256位，称为“binary256”
- 19位指数，236位有效数字
半精度（Half-Precision）：16位，称为“binary16”或“fp16”
- 1位符号位，5位指数，10位有效数字
半精度（Half-Precision）：16位，称为“bfloat16”
- 与fp16竞争
- 与fp32相同的范围！
- 用于更快的机器学习

这些不同的浮点数表示形式提供了从高精度计算到低精度、高效率计算的多种选择，适用于不同的应用场景和计算需求。

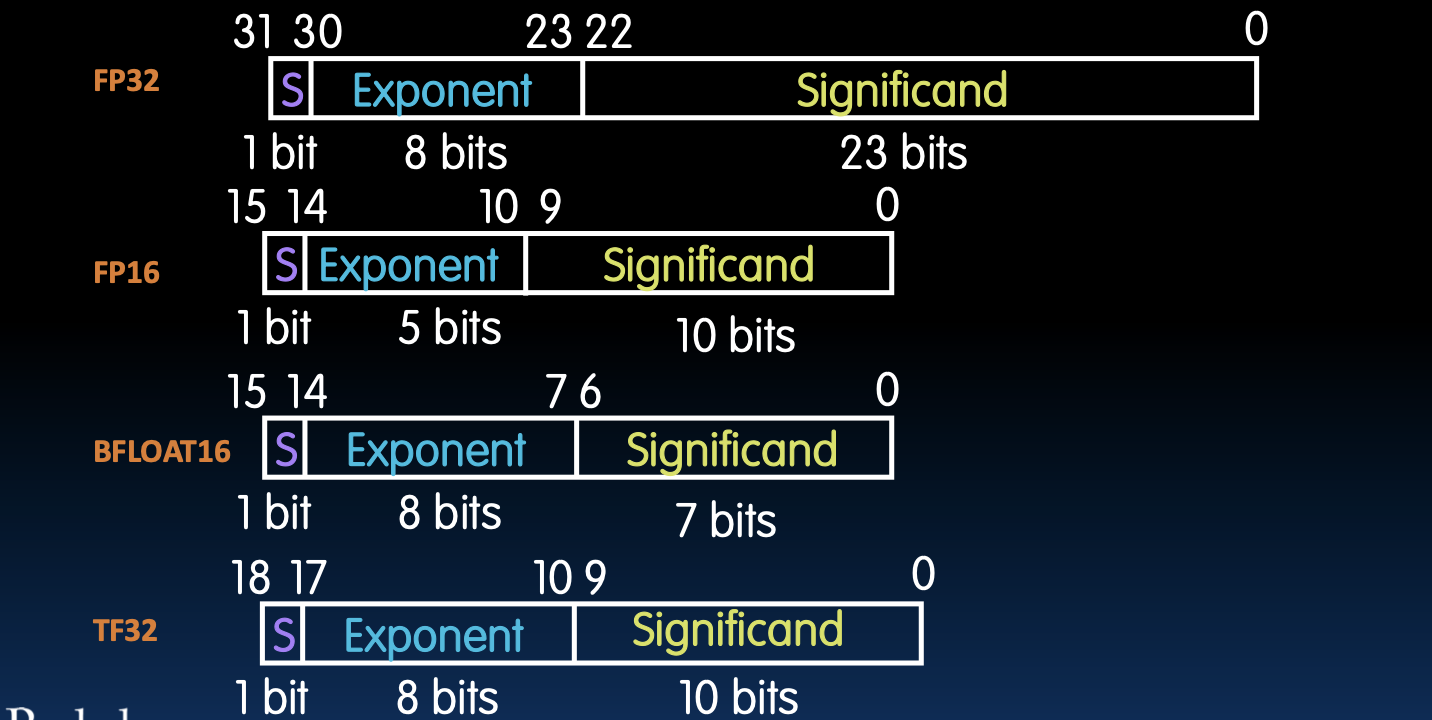
Floating Point Soup

浮点数大杂烩

FP32:

字段说明：
- 符号位（Sign bit）：1位
- 指数（Exponent）：8位
- 有效数字（Significand）：23位

FP16:

字段说明：
- 符号位（Sign bit）：1位
- 指数（Exponent）：5位
- 有效数字（Significand）：10位

BFLOAT16:

字段说明：
- 符号位（Sign bit）：1位
- 指数（Exponent）：8位
- 有效数字（Significand）：7位

TF32:

字段说明：
- 符号位（Sign bit）：1位
- 指数（Exponent）：8位
- 有效数字（Significand）：10位

详细解释和应用场景

FP32（单精度浮点数）：广泛用于一般计算，支持较大范围和精度。
FP16（半精度浮点数）：用于减少存储和计算带宽，常用于机器学习中的加速计算。
BFLOAT16（半精度浮点数的变种）：用于深度学习，保留了FP32的指数范围，但减少了有效数字的位数，以更快地进行训练。
TF32（张量浮点数）：主要用于张量计算，结合了FP16和FP32的特点，提升了计算速度和效率。

Who Uses What in Domain Accelerators?

域加速器中谁使用什么？

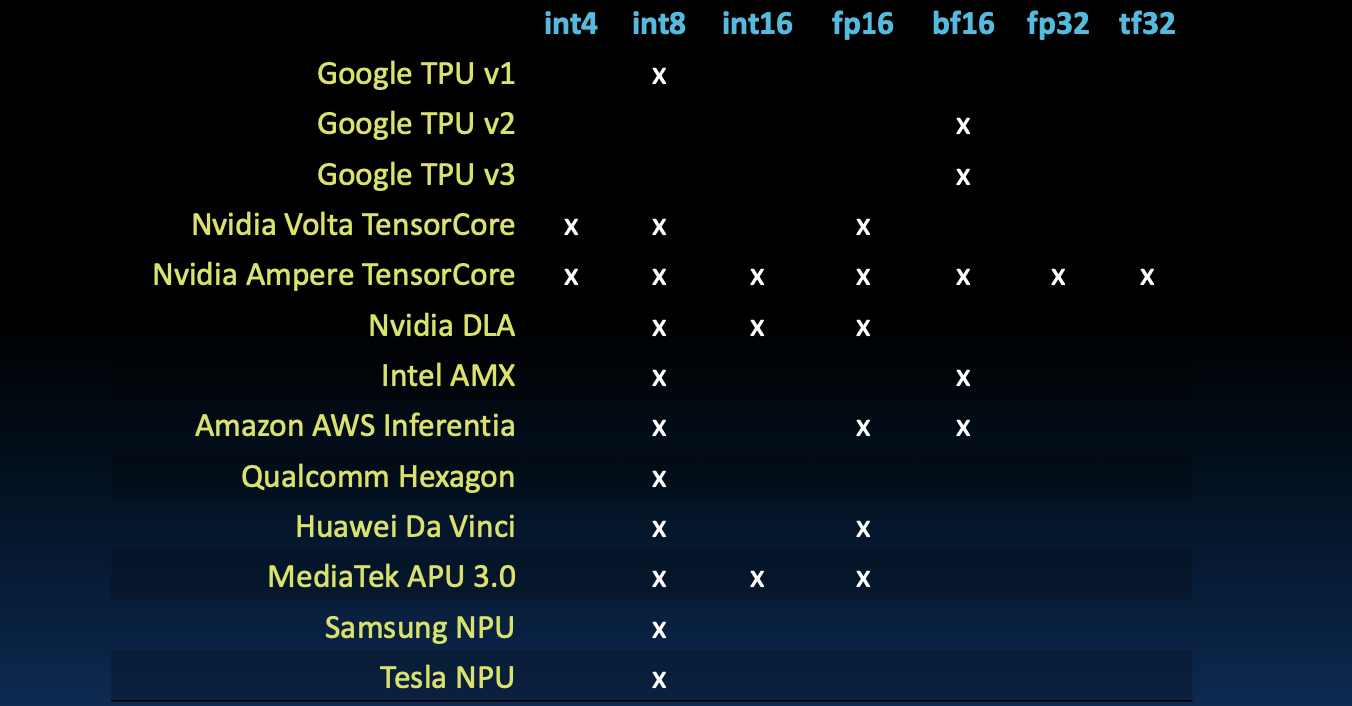
各种域加速器采用不同的浮点数表示形式以优化特定的计算任务。
- 例如，Google TPU v2和v3广泛使用int8和fp16用于机器学习加速。
- Nvidia的Volta和Ampere TensorCore采用fp16和tf32来提升张量计算的效率。
- Bfloat16在Intel AMX中使用，提供了更广泛的指数范围，非常适合深度学习任务。

Unum

Unum 数

目前为止所有的浮点数都有固定的指数和有效数字位数。

如果字段宽度是可变的会怎样？

添加一个 “u-bit” 来指示数字是精确的还是介于两个unum之间。
承诺要像浮点数对定点数一样对浮点数起到类似的作用。
声称可以节省功率！

详细解释

Unum（Universal Number）：是一种新的数值表示方法，具有可变长度的指数和有效数字。
- u-bit：用于表示数值是否精确。如果数值是精确的，u-bit为0；如果数值是近似的，u-bit为1。
- 可变长度的指数和有效数字：提供了灵活的精度和范围，可以在不增加计算复杂度的情况下处理极大或极小的数值。

Conclusion

结论

浮点数让我们…

表示同时包含整数和小数部分的数字，充分利用可用位。
存储非常大和非常小的数值的近似值。

IEEE 754 浮点标准是最广泛接受的尝试，旨在标准化此类数字的解释。

自1997年以来的每台计算机都遵循这些约定！

总结（单精度，即 fp32）：

31 30 23 22 0
s  exponent  significand
1位  8位      23位
(-1)^s × (1 + significand) × 2^(exponent-127)

指数告诉有效数字要以什么基数（2^x）进行计数（…，1/4，1/2，1，2，…）

可以存储 NaN, ±∞

详细解释

符号位（s）：1位，用于表示正负数。
指数（exponent）：8位，用于表示数值的规模，偏移值为127。
有效数字（significand）：23位，用于表示数值的精度部分。
公式：浮点数表示为 ((-1)^s \times (1 + significand) \times 2^{(exponent-127)})
- 指数部分：决定了有效数字要以什么基数进行计数，可以表示从非常小的数到非常大的数。
- 特殊值：可以表示NaN（非数字），正无穷和负无穷，确保计算的广泛性和可靠性。

通过这些解释，可以更深入地理解浮点数表示的结构和应用场景，从而更好地在计算中应用这些概念。

Ex 1: Convert Binary Floating Point to Decimal

示例1：将二进制浮点数转换为十进制

给定的二进制浮点数：

0 0110 1000 101 0101 0100 0011 0100 0010

步骤：

符号位（Sign bit）： 0（表示正数）
指数（Exponent）： 0110 1000₂ = 104₁₀
- 偏移调整：104 - 127 = -23

有效数字（Significand）：

1 + 1×2^-1 + 0×2^-2 + 1×2^-3 + 0×2^-4 + 1×2^-5 + ...
= 1 + 0.5 + 0.125 + 0.03125 + 0.0078125 = 1.6640625

计算：

1.6640625 × 2^-23 ≈ 1.986 × 10^-7

这个结果约等于2/10,000,000。

Ex 2: Convert Decimal to Binary Floating Point

示例2：将十进制转换为二进制浮点数

给定的十进制数：

-23.40625

步骤：

分解整数部分和小数部分：
- 整数部分：23
- 小数部分：0.40625
转换整数部分：

23 = 16 + 7 = 2^4 + 2^2 + 2^1 + 2^0 = 10111₂
转换小数部分：

0.40625 = 0.25 + 0.125 + 0.03125 = 0.01101₂
组合部分并规范化：

23.40625 = 10111.01101₂ = 1.011101101 × 2^4
计算偏移指数：

127 + 4 = 131 = 10000011₂

结果二进制浮点数：

1 1000 0011 011 1011 0100 0000 0000 0000

Ex 3: Represent 1/3

示例3：表示 1/3

计算：

1/3 = 0.333333…₁₀ = 0.010101010101…₂ × 2^0

二进制浮点数表示：

符号位：0
指数：127 = 01111111₂
有效数字：010101010101…

结果：

0 0111 1111 0101 0101 0101 0101 0101 0101

Understanding the Significand (1/2)

理解有效数字（1/2）

方法1：分数法（Fractions）：

十进制： 0.34₁₀

0.34₁₀ = 34₁₀ / 100₁₀
二进制： 0.11₂

0.11₂ = 11₂ / 1000₂ = 6₁₀ / 8₁₀

优势：

分数法使用较少的纯数字，使人更容易理解有效数字的含义。它强调了分子和分母的关系，适用于将小数转换为二进制的情况。

Understanding the Significand (2/2)

理解有效数字（2/2）

方法2：位置值法（Place Values）：

科学记数法：
- 十进制：
  
  1.6732 = (1×10^0) + (6×10^-1) + (7×10^-2) + (3×10^-3) + (2×10^-4)
- 二进制：
  
  1.1001 = (1×2^0) + (1×2^-1) + (0×2^-2) + (0×2^-3) + (1×2^-4)

优势：

位置值法非常适合快速计算有效数字值。通过将每个数字的值乘以它所在的位置权重，可以更直观地理解浮点数的具体表示。这种方法在处理和转换浮点数时特别有用。