Lecture 37: Dependability, Parity, ECC, RAID

Dependability via Redundancy

在这一部分，我们讨论了计算机系统中的各种故障及其对系统运行的影响。故障可以是暂时性的（例如，由电压波动引起的系统重启），也可以是永久性的（例如，硬件损坏导致的系统失效）。不论是哪种故障，都可能影响系统的正常运行，甚至导致系统崩溃。

为了解决这些问题，我们引入了第六个重要思想：通过冗余提高可靠性。冗余的核心思想是通过在系统中增加额外的资源或组件，以防止单个组件的故障导致整个系统失效。例如：

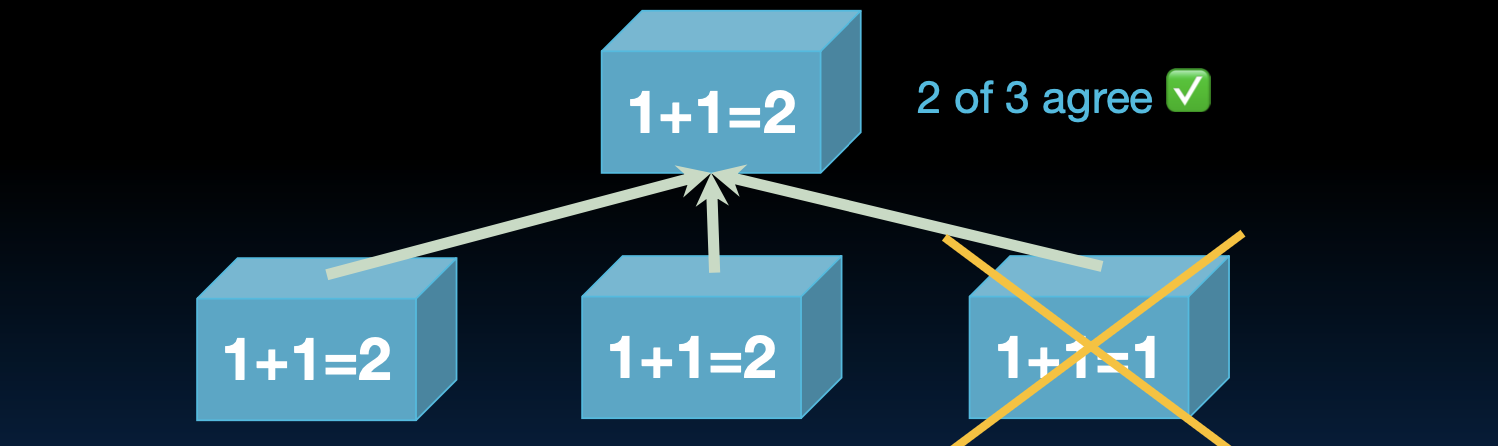
• 投票系统：在一些关键系统中，设计了三个子系统同时执行相同的计算，系统仅在至少两个子系统的结果一致时才接受该结果。这种设计可以显著提高系统的可靠性，确保即使一个子系统出现故障，系统仍能继续正常运行。

• 冗余数据中心：在互联网服务中，即使一个数据中心发生故障，另一个冗余数据中心可以继续提供服务，确保服务的持续可用性。
• 冗余磁盘：例如，通过 RAID（独立冗余磁盘阵列）技术，即使一个磁盘出现故障，数据也不会丢失，因为数据被复制到多个磁盘上。
• 冗余内存位：使用 ECC（错误纠正码）内存，即使单个位出错，也可以通过纠错机制恢复正确的数据，防止系统崩溃。

这些冗余设计可以显著提高系统的可靠性和可用性，确保系统在面对部分组件故障时仍能正常运行。

Dependability Metrics

可靠性指标

“故障”（Fault）是指系统中某个组件失效。虽然组件的失效可能导致系统整体失效，但通过适当的冗余设计，系统可以在一定程度上应对这些故障，继续提供服务。

Dependability via Redundancy: Time vs. Space

在提高系统可靠性的过程中，冗余可以通过两种主要方式实现：

• 空间冗余（Spatial Redundancy）：这是通过复制硬件组件或数据来应对硬件故障或暂时性故障。例如，RAID阵列中的磁盘冗余，通过在多个磁盘上存储相同的数据，确保即使一个磁盘故障，数据仍然安全。

• 时间冗余（Temporal Redundancy）：这是通过重复操作或重试机制来处理暂时性故障。例如，在网络传输中，如果数据包丢失，系统可以通过重新发送数据包来确保数据完整性。这种方式适用于处理短暂的、不可预见的错误。

Dependability Measures

为了评估和提高系统的可靠性，我们引入了以下关键指标：

• 可靠性（Reliability）：通过平均故障时间（MTTF）来衡量，即系统在失效前能够正常运行的平均时间。MTTF 越长，系统的可靠性越高。

• 服务中断时间（Service Interruption）：通过平均修复时间（MTTR）来衡量，即系统从故障到修复完成的平均时间。MTTR 越短，系统恢复速度越快。

• 平均故障间隔时间（MTBF）：定义为 MTTF 与 MTTR 之和，即系统两次故障之间的平均时间。MTBF 越长，系统在更长时间内保持稳定。

• 可用性（Availability）：表示系统在特定时间段内正常工作的概率。可用性公式为 MTTF / (MTTF + MTTR)。可用性越高，系统的整体性能和用户体验越好。

提高系统可用性的方法：

• 增加 MTTF：通过提高硬件和软件的质量与容错能力，延长系统无故障运行的时间。

• 减少 MTTR：通过改进诊断工具、优化维修流程和增强技术支持，缩短故障后的修复时间。

这些措施可以有效地提高系统的可用性，确保在面对各种故障时，系统能够快速恢复并保持稳定的运行状态。

可用性衡量标准

可用性（Availability）是衡量系统在特定时间段内能够正常运行的概率，其计算公式为：MTTF / (MTTF + MTTR)，通常以百分比形式表示。

• MTTF（平均故障间隔时间）和 MTTR（平均修复时间）通常以小时为单位进行衡量。
• 为了更直观地表达系统的可靠性，通常使用“每年的可用性9的个数”来表示系统的可靠性等级：
  • 1个9: 90% 可用性，意味着每年有约36天的不可用时间。
  • 2个9: 99% 可用性，意味着每年有约3.6天的不可用时间。
  • 3个9: 99.9% 可用性，意味着每年有约526分钟（约8.76小时）的不可用时间。
  • 4个9: 99.99% 可用性，意味着每年有约53分钟的不可用时间。
  • 5个9: 99.999% 可用性，意味着每年只有约5分钟的不可用时间。

随着可用性要求的增加，系统设计变得更加复杂和昂贵，因为任何一个小故障都可能影响整体系统的可用性。

可靠性衡量标准

除了可用性外，另一个重要的衡量标准是年度故障率（Annualized Failure Rate, AFR），它表示在一年内系统组件发生故障的平均次数。

• 举个例子，如果一个系统包含1000个硬盘，每个硬盘的MTTF是100,000小时：
  • 一年有365天，每天24小时，总共8760小时。
  • 计算出一年的总工作时间：1000个硬盘 * 8760小时/年 = 8,760,000设备小时。
  • 预计每年的故障次数：8,760,000设备小时 / 100,000 = 87.6次。
  • 这样，每年每1000个硬盘中的平均故障率为 87.6/1000 = 8.76%。

Google 2007年的一项研究显示，不同硬盘的实际年度故障率（AFR）在1.7%（新硬盘）到8.6%（三年使用的硬盘）之间。这表明硬盘的故障率随着使用时间的增加而上升。

失效率（FIT）率

失效率（Failures In Time, FIT）率是指在十亿（10^9）设备小时内预期会发生的故障次数。FIT 是一个用于衡量硬件设备，尤其是关键性系统（如汽车和航空电子设备）可靠性的重要指标。

• 公式为：MTBF = 1,000,000,000 × 1/FIT，即失效率和平均故障间隔时间成反比。
• 例如，如果有1000个设备在100万小时内或者100万个设备在1000小时内发生了若干次故障，那么这些故障数量就是FIT值。

在汽车安全完整性等级（ASIL）中，FIT指标对于定义不同类别车辆组件的失效率至关重要，确保在设计上达到必要的安全标准。

可靠性设计原则

为了提高系统的可靠性，设计中必须遵循一些关键原则：

• 避免单点故障（No Single Points of Failure）：确保系统的任何单个组件故障都不会导致整个系统失效。例如，通过冗余设计，系统可以继续运行，即使某个组件发生故障。
• 可靠性与Amdahl定律的关系：阿姆达尔定律同样适用于可靠性设计。不论你使系统的某一部分多么可靠，整体可靠性仍受未改进部分的限制。因此，在设计系统时，所有部分的可靠性都需要得到足够重视，而不仅仅是集中在某个特定部分。

这些设计原则在现代计算系统中至关重要，尤其是在关键任务系统中，确保系统能够在各种故障条件下保持正常运行。

Error Detection

错误检测/纠正码（Error Detection/Correction Codes）

存储系统中的错误

• 错误来源：在存储系统中，数据的正确性可能因多种原因受到影响，导致位错误。这些错误通常分为两类：
  • 软错误（Soft Errors）：这些是暂时性的错误，通常由外部环境因素（如α粒子辐射或电磁干扰）引起，导致存储单元中的某个位意外翻转。
  • 硬错误（Hard Errors）：这些错误是永久性的，通常是由于硬件损坏（如存储芯片故障）造成的。
  • 随着存储器密度的增加，DRAM中每个位的电荷越来越小，导致软错误变得更加常见。同时，硬件故障的可能性也随之增加，尤其是在大容量存储器中。

保护机制：EDC/ECC

• EDC（错误检测码）和ECC（错误纠正码）：为了应对这些错误，存储系统通常采用错误检测和纠正技术。通过在每个数据字上添加额外的位（称为冗余位），系统可以检测并纠正其中的错误。
  • 每个数据字通过附加这些冗余位映射到一个唯一的代码字（Code Word）。
  • 如果存储或传输过程中数据发生了错误，代码字将变得无效，从而可以被检测到并且在某些情况下被纠正。

块码原理（Block Code Principles）

汉明距离（Hamming Distance）

• 定义：汉明距离是指两个二进制数之间不同位的数量。它用于衡量两个代码字之间的相似度或差异度。
  • 例如，对于两个二进制数 p = 01101 和 q = 00111，它们的汉明距离为2，因为在这两个数中有两个位是不同的。

错误检测与纠正

• 代码字的构建：通过增加冗余位，代码字之间的汉明距离得以增加。最小汉明距离是用于衡量一个编码系统能够检测或纠正的错误数量的指标。
• 最小汉明距离为2的系统：如果两个有效代码字之间的最小汉明距离为2，则该系统可以检测到1位错误（如两个代码字之间相差一个位），但无法纠正该错误。如果发生两个或更多的错误，系统可能无法检测到错误的存在。

校验位：简单错误检测编码（Parity: Simple Error-Detection Coding）

偶校验（Even Parity）

• 校验位的工作原理：在数据存储前，系统会计算一个校验位（parity bit），并将其添加到数据字的末尾。这个校验位使得整个数据字的“1”的数量保持为偶数。
  • 例如，对于数据字 b7b6b5b4b3b2b1b0，系统计算所有位的异或值，生成一个校验位 p，使得当数据和校验位组合在一起时，1的总数为偶数。

校验码的局限性

• 最小汉明距离为2：校验码只能检测到奇数个错误（例如1个、3个等），而不能检测偶数个错误（如2个、4个等）。这意味着当两个不同位同时发生错误时（偶数个错误），校验码可能无法检测到这些错误。

校验位示例（Parity Example）

写入与校验过程

• 写入过程：在写入数据时，系统会根据数据的“1”的数量来确定校验位。
  • 例如，数据 0101 0101 中有4个“1”，属于偶校验，因此校验位为0，完整的数据字为 0101 0101 0。
  • 如果数据为 0101 0111，此时有5个“1”，属于奇校验，因此校验位为1，完整的数据字为 0101 0111 1。

读取与校验过程

• 读取过程：当数据被读取时，系统通过重新计算1的数量来验证数据的完整性。
  • 例如，读取 0101 0101 0 时，1的总数为4，偶校验正确，说明数据无误。
  • 如果读取到的数据为 1101 0101 0（可能由于某个位翻转造成），1的数量为5，这与偶校验不符，系统因此检测到错误。

校验位自身错误的处理

• 校验位错误的影响：如果错误发生在校验位本身，系统可能会错误地判断数据的完整性。这种情况下，简单的校验机制可能无法提供足够的保护，需要更复杂的错误检测和纠正编码（如汉明码或其他更高级的ECC技术）来应对这些问题。

通过这些机制，存储系统可以在检测到错误时采取措施，如请求重新传输数据或使用冗余信息进行纠正，从而提高数据的可靠性和系统的整体稳健性。

Error Detection and Correction

假设想要纠正一个错误

汉明码（Hamming Code）

理查德·汉明（Richard Hamming）发明了一种称为汉明码（Hamming Code）的错误纠正码，它的设计初衷是通过引入最小汉明距离为3的编码方案，能够有效地纠正单个比特错误，并检测双比特错误。汉明码的核心思想是通过在数据中添加冗余位来实现错误检测和纠正。

• 错误纠正：汉明码能够纠正一个单比特错误。具体来说，如果传输过程中一个比特发生了翻转，汉明码可以通过计算并识别出错误位的位置，然后将其纠正回正确的值。
• 错误检测：汉明码不仅能够纠正单个错误，还能检测到双比特错误。当有两个比特错误发生时，汉明码会发现数据未通过其编码检查，从而发出错误信号，提示存在数据损坏。

汉明码的背景

汉明的工作背景是使用早期继电器计算机的时代，这些计算机往往因为硬件的局限性导致频繁的读取错误。例如，卡片读取器在读取穿孔卡片数据时容易出错，这使得汉明不得不反复手动重启计算机来处理错误。面对这些问题，他着手开发了一种能够自动检测和纠正这些错误的编码方案，即汉明码。在1950年，汉明发表了关于这种技术的论文，为现代错误检测与纠正技术奠定了基础。

检测/纠正码的概念（Detecting/Correcting Code Concept）

错误检测与纠正

在错误检测与纠正码的概念中，数据传输过程中可能会由于各种原因（如噪声或硬件故障）导致比特翻转。为了确保数据的完整性，系统采用编码方案来检测并纠正这些错误。

• 检测：当数据未通过预期的码字检查时，系统可以确定数据已经遭到破坏。检测的核心是利用比特模式的空间，其中有效的码字仅占这个空间的一小部分。如果数据在传输过程中被修改，结果可能会落在无效的比特模式上，从而触发错误检测。
• 纠正：纠正过程涉及将错误的比特模式映射回最近的有效码字。这种映射通常基于汉明距离，系统通过找到与错误码字最近的有效码字来纠正错误。

在比特模式空间中，所有可能的比特组合形成了一个大的空间，但只有一部分是有效的码字。系统通过检测并纠正错误，确保数据的可靠性。

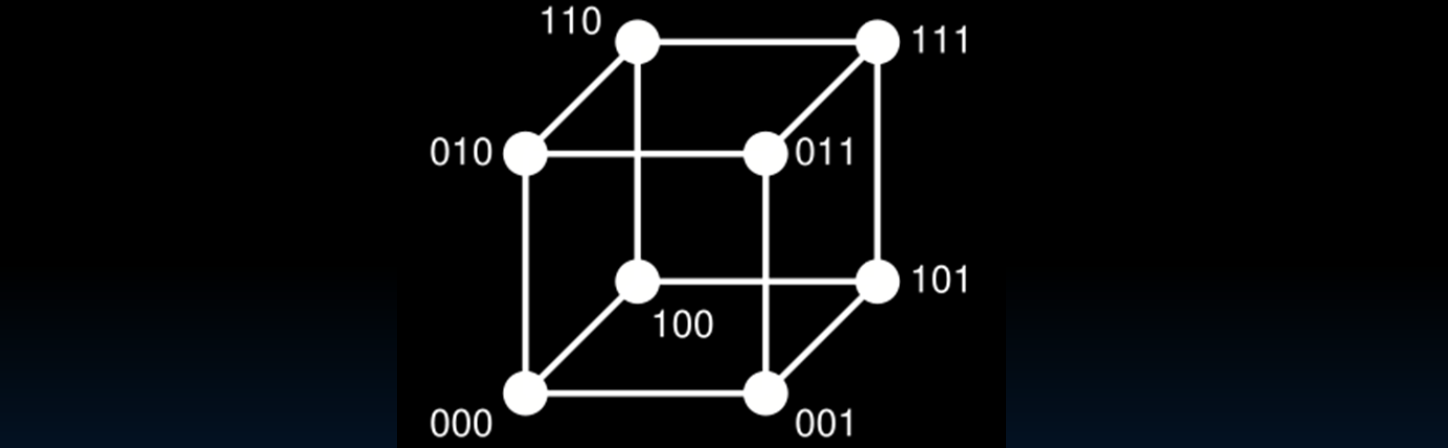
汉明距离：八个码字（Hamming Distance: Eight Code Words）

汉明距离的基本概念

汉明距离表示两个二进制码字之间不同位的数量。在一个三位二进制码字的空间中，每个点代表一个可能的码字，相邻点之间的边表示它们之间的汉明距离为1。这个概念在错误检测和纠正中起着至关重要的作用。

汉明距离 2 的码字设计与错误检测

这张图展示了使用汉明距离为2的码字来进行错误检测和纠正的原理。我们将分两个部分来讨论：有效码字与无效码字的设计、1/2的码字为何有效，以及如何进行错误检测与纠正。

1. 有效码字与无效码字的设计

在编码理论中，码字是用来表示信息的二进制字符串。为了能够检测和纠正错误，我们通过特定的设计来将某些二进制字符串定义为有效码字，而其他的则被认为是无效码字。

• 有效码字：在这张图中，黄色节点（如 000, 011, 101, 110）代表有效码字。这些码字的设计使得任何两个有效码字之间的汉明距离至少为2。这意味着，从一个有效码字变成另一个有效码字，至少需要改变两个比特位。

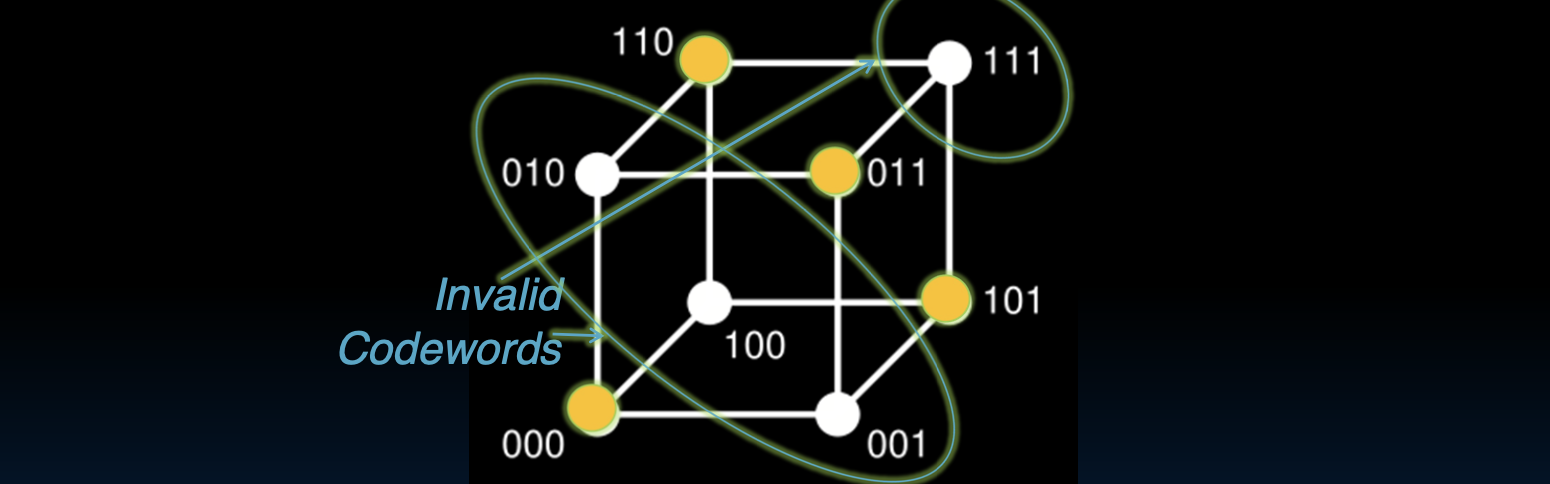
• 无效码字：白色节点（如 001, 010, 100, 111）表示无效码字。它们不属于预定义的有效码字集合。

2. 1/2 的码字为何有效？

在这种编码方案中，所有可能的二进制字符串中，只有一半是有效码字。这是为了确保有效码字之间的汉明距离为2。具体原因如下：

• 防止错误码字变为另一个有效码字：由于有效码字之间的汉明距离至少为2，任何一个有效码字发生单比特错误（即只改变一位）后，都不会变成另一个有效码字，而是变成一个无效码字。这就保证了单比特错误不会使得一个有效码字被误认为是另一个有效码字。

• 保证纠错的唯一性：如果我们只使用一半的码字作为有效码字，任何一个无效码字只会与一个有效码字的汉明距离为1（即相差一位）。这意味着当我们检测到一个无效码字时，可以确定唯一的有效码字来纠正错误。

因此，为了能够正确地检测和纠正单比特错误，我们必须牺牲一部分码字的使用权，使得只有一半的码字被用作有效码字。这确保了可靠的错误检测和纠正。

错误纠正

下图只有 000 和 111 这两个码字是有效的，而其他所有码字都是无效的。在这种设计中，任何无效码字都与唯一一个有效码字的汉明距离为1。

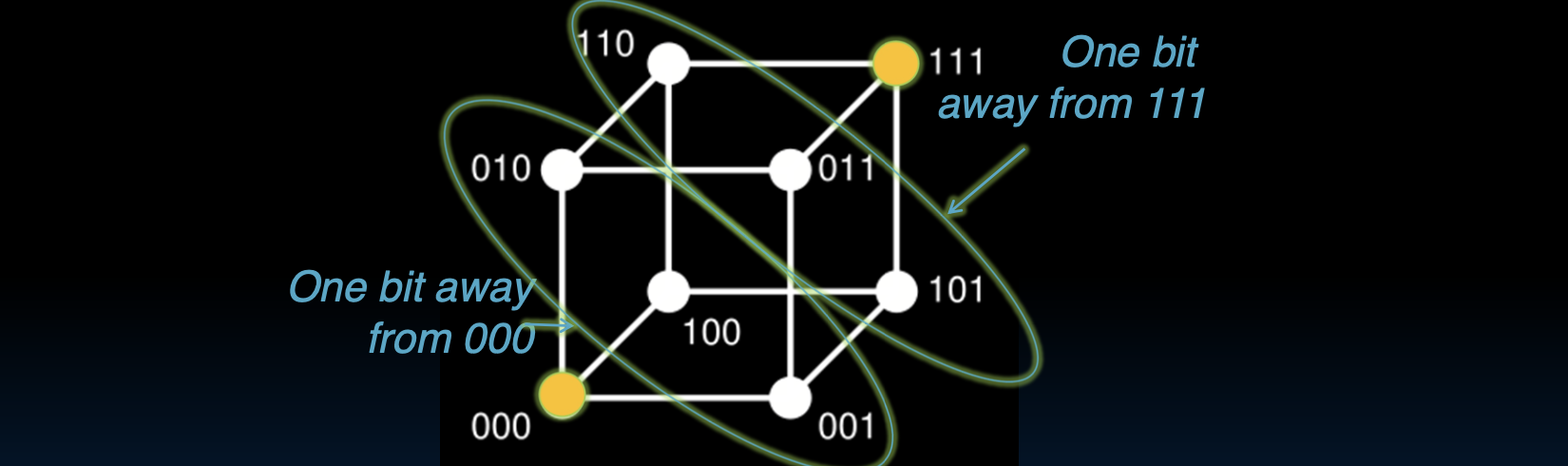
错误检测：

• 单比特错误检测：假设传输过程中发生了单比特错误，导致码字变成了无效码字（比如 000 变成 001）。由于所有无效码字都与任一有效码字的汉明距离至少为1，因此可以检测出错误。

错误纠正：

• 单比特错误纠正：当一个无效码字被检测到时，我们可以根据与哪个有效码字的汉明距离为1来纠正它。例如，如果收到的码字是 001，我们知道 001 与 000 的汉明距离为1，因而可以将 001 纠正为 000。

Error Correcting Code (ECC) Examples

汉明错误校正码概述

汉明错误校正码（Hamming ECC）是一种用于检测和纠正数据传输或存储过程中单比特错误的编码技术。通过在数据中插入校验位，汉明码能够在数据受到单比特错误影响时检测并纠正这些错误，从而提高数据传输和存储的可靠性。

在汉明编码过程中，校验位被插入到数据的特定位置，以确保在错误发生时可以检测到错误。

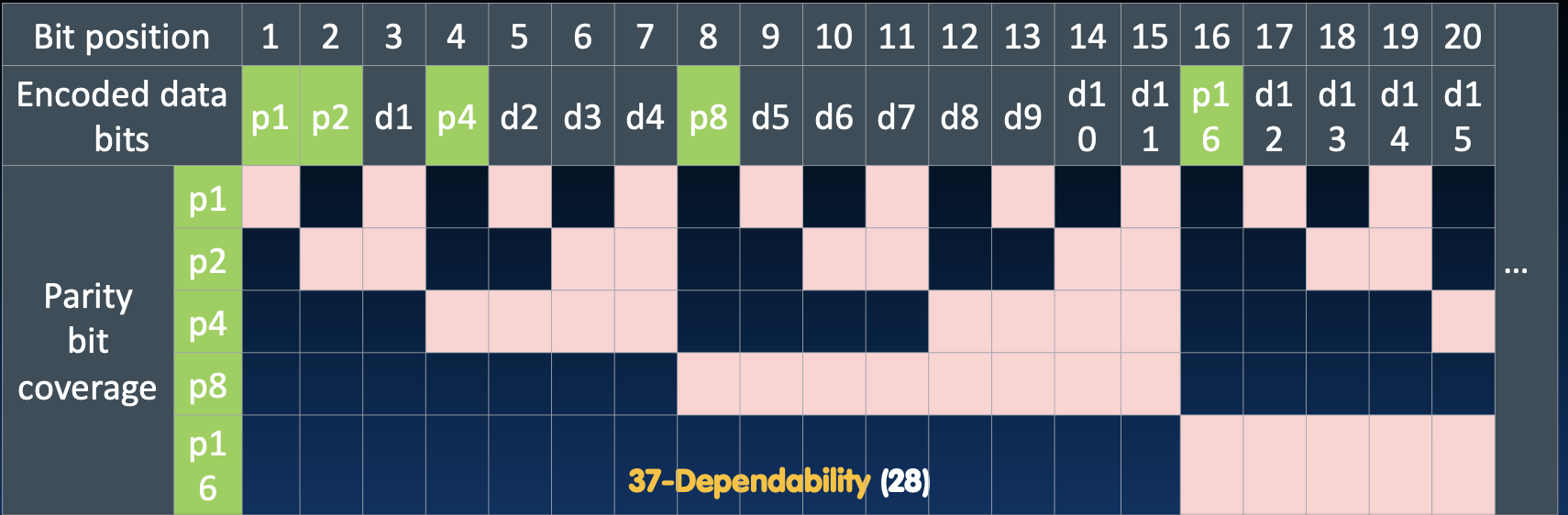
1. 校验位（Parity Bits）的插入位置

校验位插入在那些二进制表示中是2的幂次方的位置。例如：

• p1 位插入在第1位（对应二进制 0001）。
• p2 位插入在第2位（对应二进制 0010）。
• p4 位插入在第4位（对应二进制 0100）。
• p8 位插入在第8位（对应二进制 1000）。
• p16 位插入在第16位（对应二进制 10000）。

这些位置都是2的幂，选择这些位置是因为它们可以唯一地覆盖其他数据位，并且它们在二进制数中的低位权重决定了它们覆盖的范围。

2. 校验位的覆盖范围

每个校验位负责检查一组特定的数据位。这些覆盖范围是根据校验位在二进制表示中的低位权重来决定的。

• p1：覆盖所有二进制表示的最右边一位为1的位置（即1、3、5、7、9、11、13、15…）。这意味着它负责检测这些位置的数据位。
• p2：覆盖所有二进制表示的次低位为1的位置（即2、3、6、7、10、11、14、15…）。
• p4：覆盖所有二进制表示的第3位为1的位置（即4、5、6、7、12、13、14、15…）。
• p8：覆盖所有二进制表示的第4位为1的位置（即8、9、10、11、12、13、14、15…）。
• p16：覆盖所有二进制表示的第5位为1的位置（即16及以上…）。

3. 数据位的插入位置

数据位（d1, d2, d3…）插入在非校验位的位置。这些位是需要传输的实际数据，经过汉明码编码后，这些数据位与校验位交替出现。

例如：

• d1 插入在第3位（因为第1位是p1, 第2位是p2）。
• d2 插入在第5位（第4位是p4）。
• d3 插入在第6位，以此类推。

4. 校验位的计算

每个校验位负责计算并校验它覆盖的数据位之和的奇偶性（根据需要，可以是偶校验或奇校验）。如果这些数据位发生错误，校验位就会发现不匹配，从而帮助定位出错的比特位。

5. 为什么选择这些位置？

选择这些特定的插入位置（2的幂次方）和覆盖范围是为了确保每个数据位都可以被唯一确定地定位。通过对校验位的组合分析，可以精确找出发生错误的具体位。

汉明 ECC 编码示例

假设我们有一个字节的数据10011010，在汉明码的编码过程中，我们首先在指定的位置插入校验位的占位符。对于一个12位的编码，我们需要插入4个校验位。

假设编码的各个位位置如下：

_ _ 1 _ 0 0 1 _ 1 0 1 0
1 2 3 4 5 6 7 8 9 a b c - 位位置序号（从左到右）

在这个表示中，位1、位2、位4、位8是校验位的占位符，其他位置保留给数据位。

接下来，我们计算各个校验位的值，这些值通过检查其覆盖的特定数据位来确定。每个校验位覆盖一组数据位，并确保这组数据位的奇偶性。

例如：

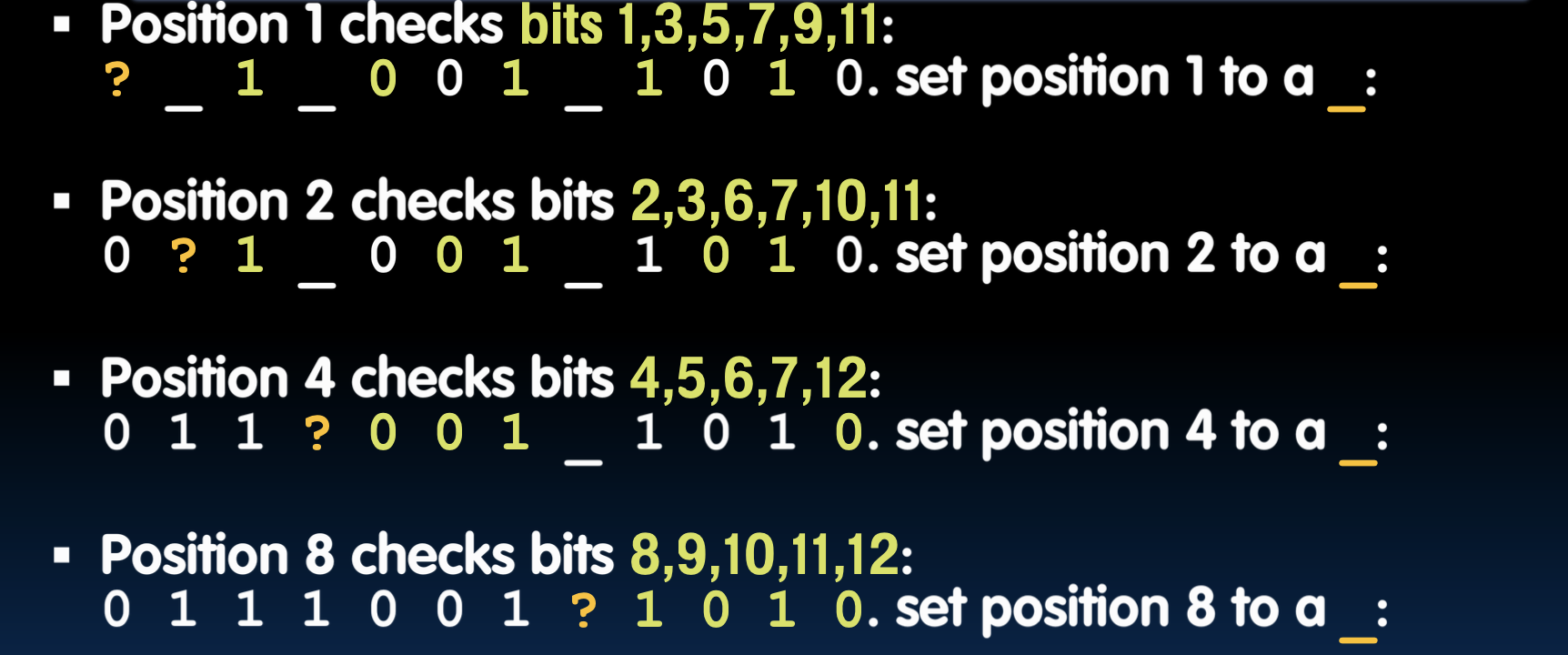
• 校验位1（位1）覆盖位1, 3, 5, 7, 9, 11：计算结果为0。
• 校验位2（位2）覆盖位2, 3, 6, 7, 10, 11：计算结果为1。
• 校验位4（位4）覆盖位4, 5, 6, 7, 12：计算结果为0。
• 校验位8（位8）覆盖位8, 9, 10, 11, 12：计算结果为1。

这些校验位的值被插入到数据串中的相应位置，从而形成完整的汉明码。

最终的编码结果为011100101010，其中校验位和数据位被交错排列。通过这种方式，汉明码确保在数据传输或存储过程中发生单比特错误时，这些错误可以被检测并纠正。

汉明 ECC 解码示例

在解码过程中，接收到的数据可能包含单比特错误。假设我们接收到的数据为011100101110，它包含了数据位和校验位。接下来的步骤是检查这些校验位是否满足其奇偶性条件，以确定是否存在错误。

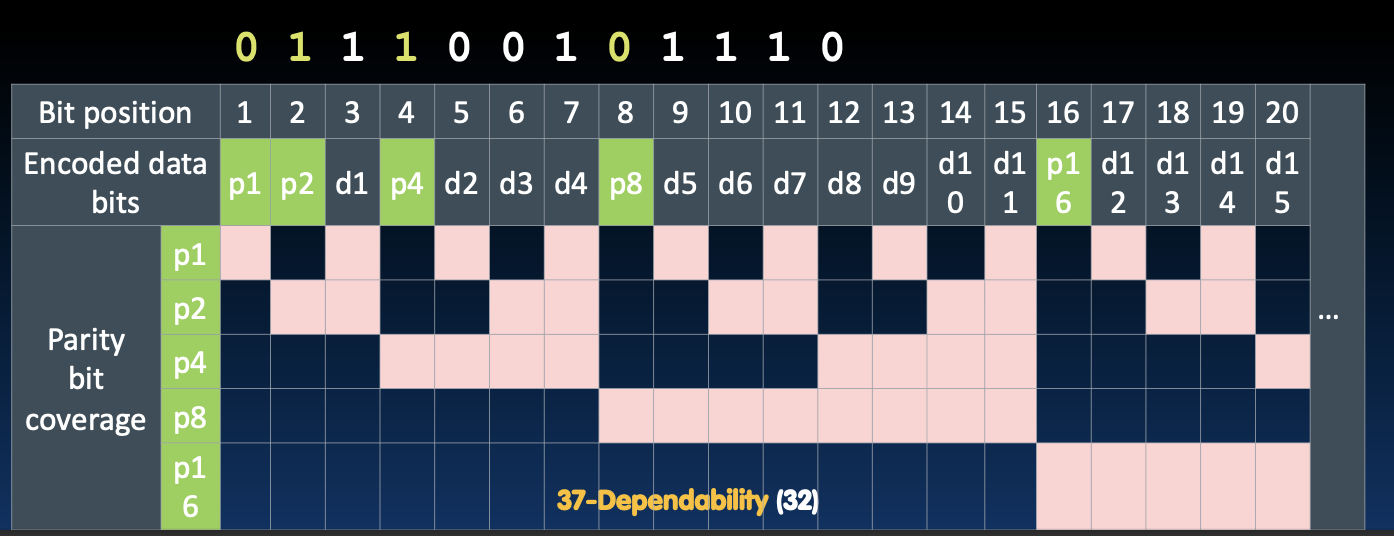
为了检查错误，我们重新计算接收数据中每个校验位覆盖的位，并将计算结果与接收到的校验位进行比较。

• 校验位2：如果覆盖的数据位中出现了错误，这意味着校验位2显示有问题。
• 校验位8：如果覆盖的数据位中也出现了错误，这意味着校验位8显示有问题。

根据汉明码的纠错机制，当多个校验位都显示错误时，可以通过这些校验位的位置组合确定错误发生的确切位置。在这个例子中，位置 8 + 2 = 10，即第10位的数据出现了错误。

根据错误检查得出的错误位置信息，我们可以将第10位的数据位从1更正为0，从而将收到的编码修正为011100101010。这个过程成功修复了单比特错误。

经过错误校正后的数据位现在是正确的，可以继续进行进一步的处理或使用。汉明码的这种错误检测与纠正方法确保了数据在传输或存储中的可靠性，大大降低了由于单比特错误而导致数据不一致的风险。

通过这种方式，汉明码成为了在计算机存储和通信领域中广泛应用的一种错误检测与纠正技术。

Redundancy with RAID

多位错误的处理

当数据传输或存储过程中出现超过2位的错误时，汉明码等简单的纠错方法就不再适用了。这时，我们需要使用更复杂的错误检测和纠正机制，如双错误纠正、三错误检测（DECTED）码。这些方法能够检测和纠正更多位数的错误，适应更加复杂的错误模式。以下是几种常用的高级纠错技术：

1. 循环冗余校验（CRC）：
   • 原理：CRC是一种基于多项式除法的错误检测方法，通过对数据进行计算生成校验值，并将其附加在数据之后。当接收方收到数据时，再次计算校验值并与接收到的校验值进行比较。如果两者不一致，说明数据发生了错误。
   • 应用：CRC广泛应用于网络传输、存储设备中，能够有效地检测突发错误。
2. 交错存储（Interleaving）：
   • 原理：交错存储通过将数据在存储或传输时分散存放，使得连续位的错误不会集中在一个数据块中，减少了单一错误影响的位数，从而使得简单的纠错码也能有效工作。
   • 应用：常用于磁带、CD-ROM等存储介质中，以增强数据的可靠性。
3. 高级编码方法：
   • 低密度奇偶校验码（LDPC）：这是一种现代纠错码，广泛应用于Wi-Fi、5G等高数据速率的通信标准中，能够有效地处理高比特率的错误。
   • Reed-Solomon码：用于CD、DVD、QR码等介质中，擅长纠正连续错误和突发性错误。

这些高级错误纠正技术使得系统在面对突发性多位错误时，能够更好地保证数据的完整性和可靠性。

使用RAID实现冗余

RAID（独立磁盘冗余阵列）是一种通过将数据分布在多个磁盘上来提供冗余和提高可用性的方法。RAID通过条带化（striping）数据并结合冗余技术，即使某个磁盘发生故障，系统仍然可以继续运行，并能够恢复丢失的数据。以下是几种常见的RAID配置：

RAID 1：磁盘镜像/影子

• 工作原理：RAID 1通过将每个磁盘的内容完整地复制到另一个磁盘上，形成一个“镜像”磁盘。这样，即使一个磁盘发生故障，系统仍然可以从镜像磁盘中读取数据。
• 优点：
  • 高可用性：即使一个磁盘失效，数据仍然安全可用。
  • 读取优化：可以同时从多个磁盘读取数据，提高读取速度。
• 缺点：
  • 存储成本高：需要双倍的存储容量来存储镜像数据。
  • 写入速度较慢：写操作需要同时更新两个磁盘，可能导致写入性能下降。

RAID 3：奇偶校验磁盘

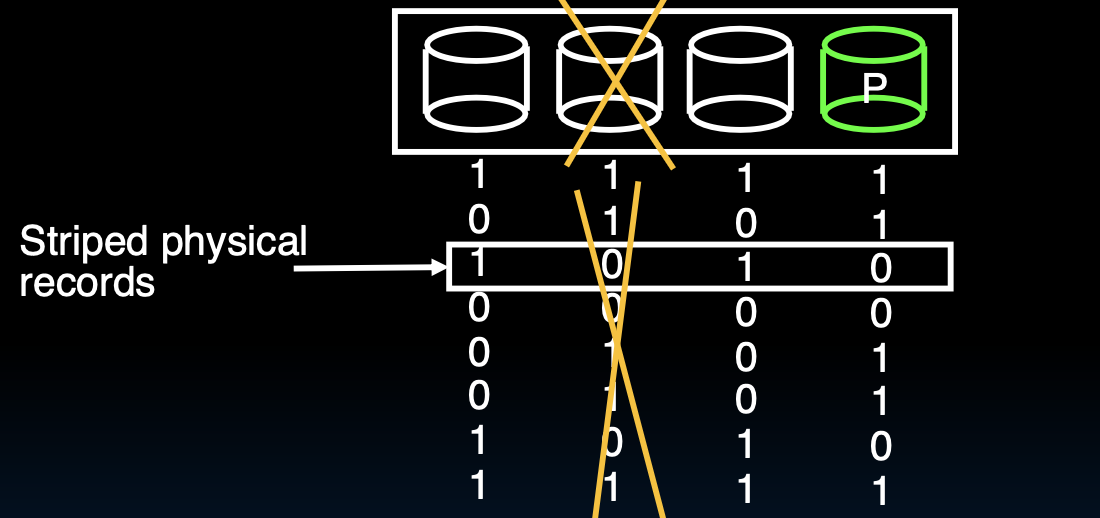
• 工作原理：RAID 3利用一个专用的奇偶校验磁盘（P盘）存储其他所有数据磁盘的奇偶校验信息。奇偶校验是对数据进行mod 2的和运算，生成校验位。当一个磁盘发生故障时，可以通过其他磁盘的数据和奇偶校验信息重建丢失的数据。
• 优点：
  • 高效的冗余：奇偶校验磁盘提供了较好的数据冗余能力，同时只需要额外一个磁盘来存储冗余信息。
• 缺点：
  • I/O瓶颈：由于奇偶校验磁盘需要参与每次写操作，因此在大量小数据块的I/O操作时，奇偶校验磁盘可能成为性能瓶颈。
  • 重建时间长：当一个磁盘发生故障时，重建数据需要计算大量的奇偶校验信息，过程较为耗时。

RAID 4：优化的高I/O速率奇偶校验

RAID 4是对RAID 3的改进，采用了与RAID 3相同的基本思想，即使用一个专用的奇偶校验磁盘来存储冗余信息。然而，RAID 4通过将数据块分割并以条带化的方式分布在多个磁盘上，显著提高了系统的I/O速率，特别是在大数据量的读取操作中。每个磁盘可以独立读取其上的数据块，因此在读操作中多个磁盘可以并行工作，从而提高了整体数据读取速度。

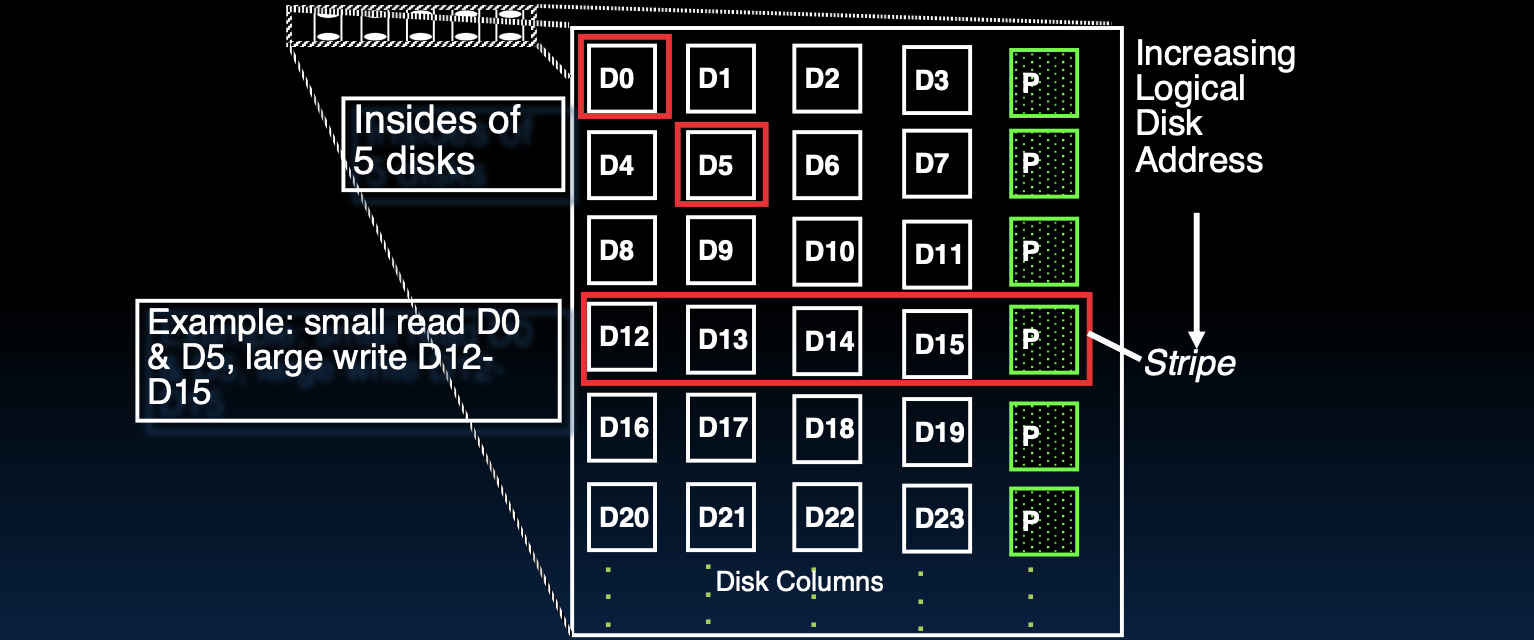
• 优点：
  • 高效的读取性能：由于数据分布在多个磁盘上，读取操作可以并行执行，从而显著提升了系统的读取速率。
  • 简单的奇偶校验管理：只需一个专用的奇偶校验磁盘来管理冗余数据，结构相对简单。
• 缺点：
  • 奇偶校验磁盘瓶颈：所有写操作都需要更新奇偶校验磁盘，因此频繁的写操作可能会导致奇偶校验磁盘成为系统瓶颈，影响整体写入性能。
  • 单点故障风险：如果奇偶校验磁盘出现故障，系统将失去所有数据的冗余保护，直到故障磁盘被替换并重新生成奇偶校验信息。

RAID 5：提升写入效率的分布式奇偶校验

RAID 5是在RAID 4的基础上进一步优化的版本，它的设计目的是解决RAID 4中奇偶校验磁盘成为瓶颈的问题。RAID 5通过将奇偶校验信息均匀地分布在所有磁盘上，使得每个磁盘既存储数据块，也存储奇偶校验块。这种分布式的奇偶校验机制使得RAID 5在处理写操作时更加高效，因为写操作可以在多个磁盘上并行进行，从而消除了单个奇偶校验磁盘的瓶颈。

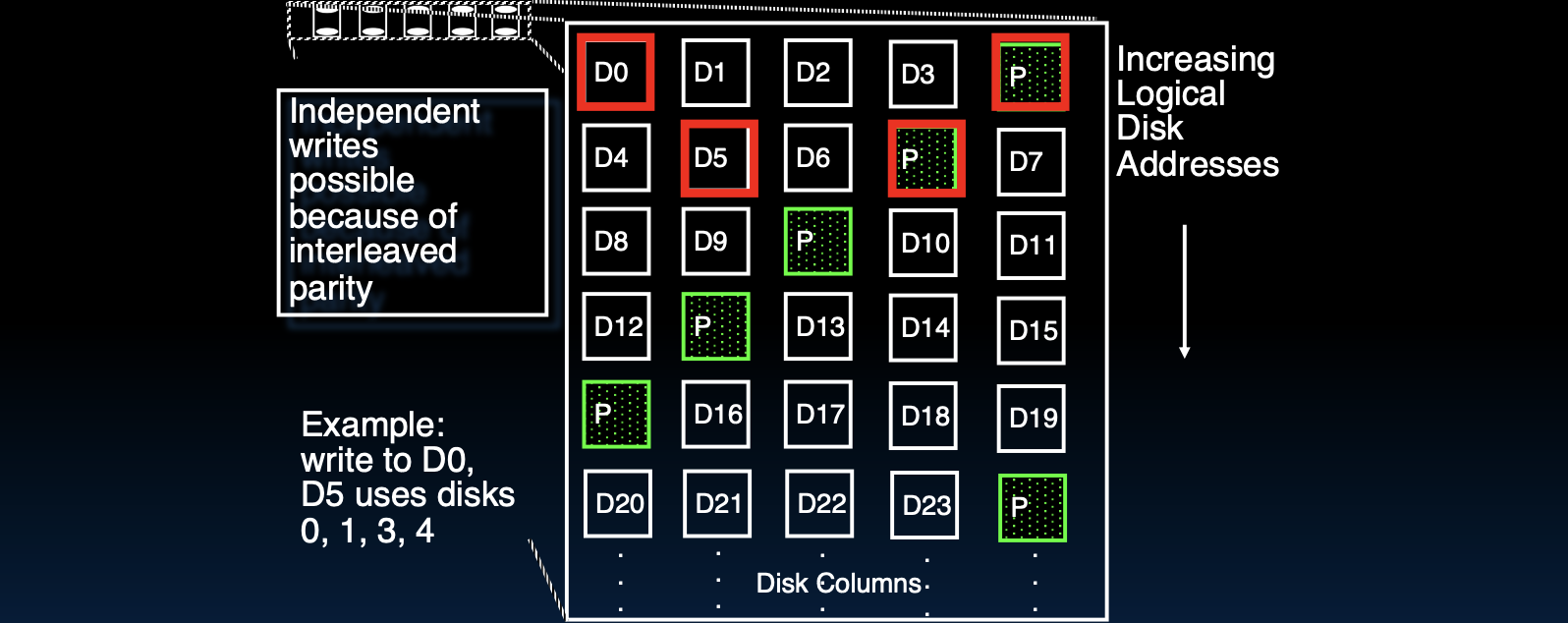
• 奇偶校验更新机制：
  • 全盘读取更新：RAID 5在进行写操作时，可以通过读取其他数据磁盘的内容重新计算奇偶校验，然后更新奇偶校验数据。
  • 差异更新：如果已知旧数据和新数据之间的差异，RAID 5可以直接更新对应的奇偶校验数据，而无需重新计算整个奇偶校验，从而加快了写操作的速度。
• 优点：
  • 高并行写入性能：通过将奇偶校验数据分布到所有磁盘上，RAID 5显著提高了写入操作的效率，特别是在处理小数据块时更为明显。
  • 无单点故障的冗余设计：由于奇偶校验数据分布在多个磁盘上，即使一个磁盘故障，系统仍然能够通过其他磁盘的数据和奇偶校验信息重建丢失的数据。
• 缺点：
  • 复杂的重建过程：当一个磁盘出现故障时，重建数据的过程需要涉及多个磁盘的数据读取和奇偶校验计算，可能会导致系统性能下降，尤其是在大数据量的系统中。
  • 写入性能受限：虽然RAID 5优化了写入性能，但在极端情况下，写入操作仍然可能受到奇偶校验更新的影响，导致性能下降。

总结

RAID技术的核心理念是通过冗余来实现系统的可靠性和可用性。通过引入空间冗余（如额外的磁盘存储奇偶校验数据）和时间冗余（如错误重试机制），RAID能够有效地提高系统的容错能力，确保即使在部分硬件故障的情况下，系统仍能正常运行。

• 关键指标：
  • 可靠性（Reliability）：通过度量如平均故障间隔时间（MTTF）、年度故障率（AFR）和故障次数（FIT）来评估系统的可靠性。
  • 可用性（Availability）：通过公式MTTF/(MTTF + MTTR)来计算系统在某一时间段内的可用性，即系统正常运行的时间百分比。

RAID的不同版本（如RAID 1、RAID 4、RAID 5）通过不同方式实现数据冗余和容错能力。特别是RAID 5，通过将奇偶校验数据分布在所有磁盘上，显著提高了写入操作的效率，适用于大多数企业级存储环境。RAID技术的广泛应用大大提高了数据存储系统的可靠性和可用性，使其成为现代数据中心和存储系统的重要组成部分。