Lecture 16: SDS State, FSMs

Introduction to Synchronous Digital Systems (SDS) State

同步数字系统（SDS）状态简介

在同步数字系统中，状态元素（State Elements）是用于存储信息的关键组件。它们与时钟信号协调工作，以确保数据的有序流动和处理。

Accumulator

累加器

Uses for State Elements

状态元素的用途包括：

存储值的地方：
- 用于存储某些不确定时间段内的值，例如：
  - 寄存器文件（如RISC-V中的x0-x31）
  - 内存（缓存和主内存）
- 状态元素可以在不丢失数据的情况下存储临时计算结果，等待下一步操作。
控制信息流动：
- 在组合逻辑块之间控制信息的流动。
- 状态元素用于在组合逻辑块的输入处保留信息的移动，允许有序传递。通过时钟信号控制数据的传递时机，确保每一步计算都在正确的时间发生。

Accumulator Example

累加器是用于对一系列数值进行累加的电路或算法。

问题的提出

Why do we need to control the flow of information? 为什么我们需要控制信息流？

控制信息流是为了确保每个输入的值能够被正确处理和累加，并在预期的时间内输出结果。

需求（Want）

我们希望实现以下目标：

s = 0;
for (i = 0; i < n; i++) {
    s = s + x_i;
}

这段代码的意思是，我们从0开始，将一系列值 \(x_i\) 逐一累加到变量 \(s\) 中。

假设（Assume）

每个 \(x\) 值按顺序依次应用，每个时钟周期一个。
在 \(n\) 个时钟周期之后，累加的结果 \(S\) 会出现在输出端。

图示中的模块

图中展示了一个累加器模块：

输入： \(x_i\) 表示输入的数值序列。
Sum：累加器模块，负责对输入的数值进行累加。
输出： \(S\) 表示累加的结果。

工作原理

初始状态：
- 初始化累加器 \(S\) 为0。
每个时钟周期：
- 将当前的输入值 \(x_i\) 输入到累加器中。
- 累加器将输入值 \(x_i\) 加到当前的累加和 \(S\) 上。
- 更新累加和 \(S\) 的值。
结束状态：
- 在 \(n\) 个时钟周期之后，累加的结果 \(S\) 会在输出端显示。

详细解释

控制信息流：在这个过程中，我们需要确保每个输入值 \(x_i\) 在正确的时钟周期被输入到累加器中，这就是控制信息流的意义。错误的时序会导致错误的累加结果。
累加器模块：累加器模块通过不断地将输入值与当前累加和相加，逐步得到总和。
时钟周期：每个时钟周期内，累加器处理一个输入值。这意味着如果有 \(n\) 个输入值，则需要 \(n\) 个时钟周期来完成所有输入值的累加。

First try…Does this work?

Nope!

原因1：如何控制for循环的下一次迭代？
原因2：如何表示S=0？

初次尝试通过反馈连接将输出值返回到输入，但缺乏控制机制，导致问题无法解决。

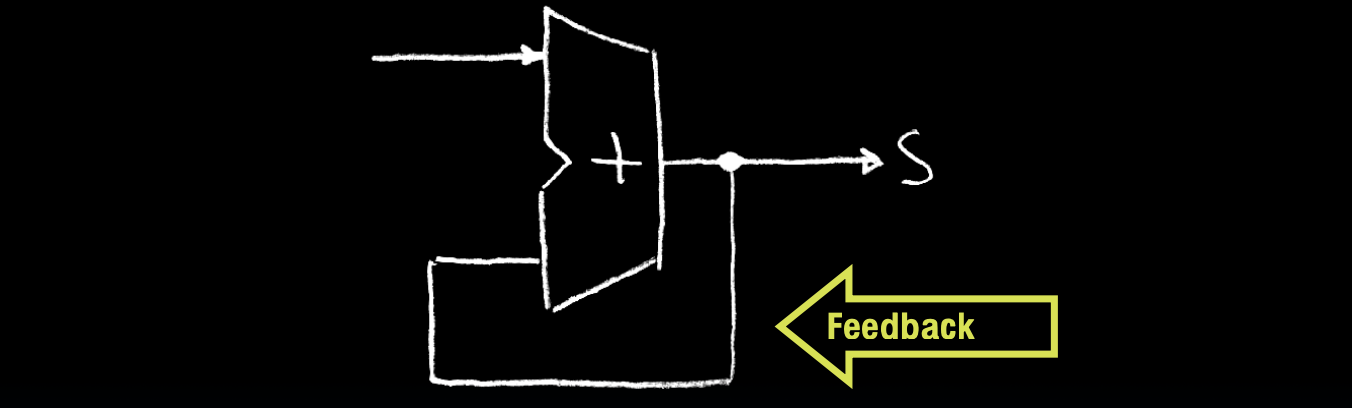
Second try…How about this?

解决方案：

使用寄存器来延缓数据传输到加法器的过程。

在此设计中，寄存器用于保持中间结果，确保每次时钟信号到来时，寄存器中的值正确传输到加法器。
通过寄存器的使用，可以有效控制加法器的每次运算。

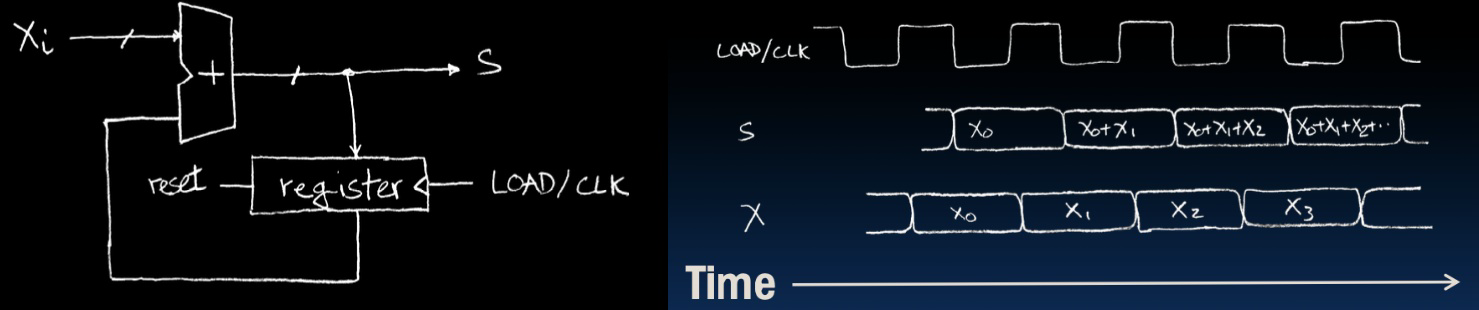
粗略时序图：

显示了时钟信号（LOAD/CLK）、累加结果（S）以及输入值（X）的关系。
通过时钟信号的控制，每个输入值X_i按顺序在每个时钟周期传递并累加，最终在输出S上得到总和。

这种设计使得数据在不同的时钟周期内有序传递和累加，解决了最初设计中的控制问题。

Register Details Flip-flops

Register Details…What’s Inside?

寄存器的内部结构

寄存器由多个触发器（Flip-Flop）组成。每个触发器存储一个位。
触发器被称为“Flip-Flop”，因为其输出在0和1之间反复变化。
D表示“数据”（data），Q表示“输出”（output）。
这种触发器也称为“D型触发器”（D-type Flip-Flop）。

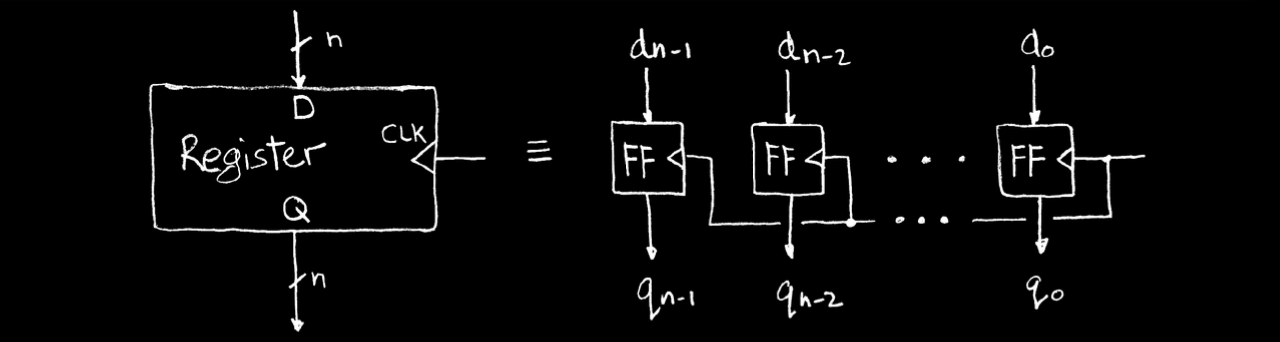
寄存器工作原理

每个D型触发器在时钟信号的上升沿（rising edge）采样输入数据，并将其传输到输出。
在其他时间，输入数据被忽略。这种机制确保了数据的稳定性和一致性。

在现代计算机系统中，寄存器用于暂存指令、操作数和中间结果等。寄存器的性能直接影响CPU的速度和效率。

What’s the Timing of a Flip-flop? (1/2)

D型触发器的时序

边沿触发D型触发器：这个触发器是“上升沿触发”（rising edge-triggered），也称为“正边沿触发”（positive edge-triggered）。
当时钟信号的上升沿到来时，输入数据d被采样并传输到输出q。在其他时间，输入数据d被忽略。

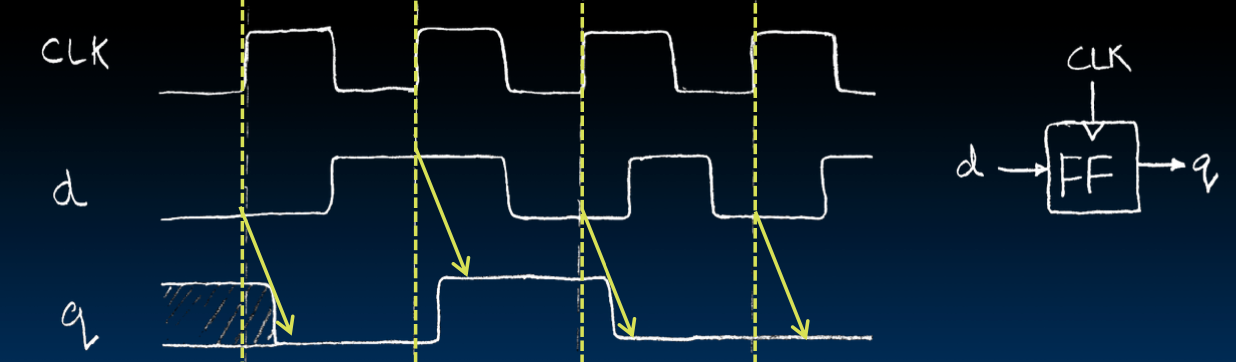
示例波形

CLK：时钟信号。
d：输入数据。
q：输出数据。

波形图展示了在时钟信号上升沿时，输入数据d如何被采样并传输到输出q。在时钟的上升沿，D型触发器捕获输入数据并在Q端输出。

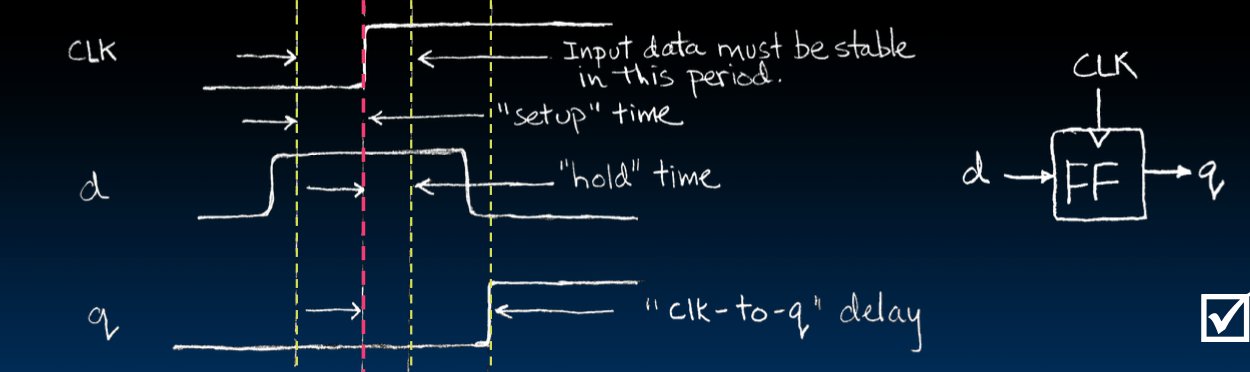
示例波形（更详细）

波形图展示了输入数据在被采样前需要稳定一段时间（setup time），并且在被采样后需要保持一段时间（hold time）。
输入数据到输出数据之间的延迟被称为“clk-to-q”延迟。

这些时序参数对设计稳定可靠的数字电路至关重要。例如，在设计高速电路时，需要特别注意这些参数，以确保数据在适当的时间点被正确采样和传输。

Accumulator Revisited

Accumulator Revisited (proper timing 1/2)

累加器的正确时序（1/2）

复位输入(reset)：寄存器的复位输入用于将寄存器中的所有值强制为零（优先于D输入）。
\( S_{i-1} \)：保存第\( i-1 \)次迭代的结果。
时序分析：从寄存器的输出开始分析电路时序。

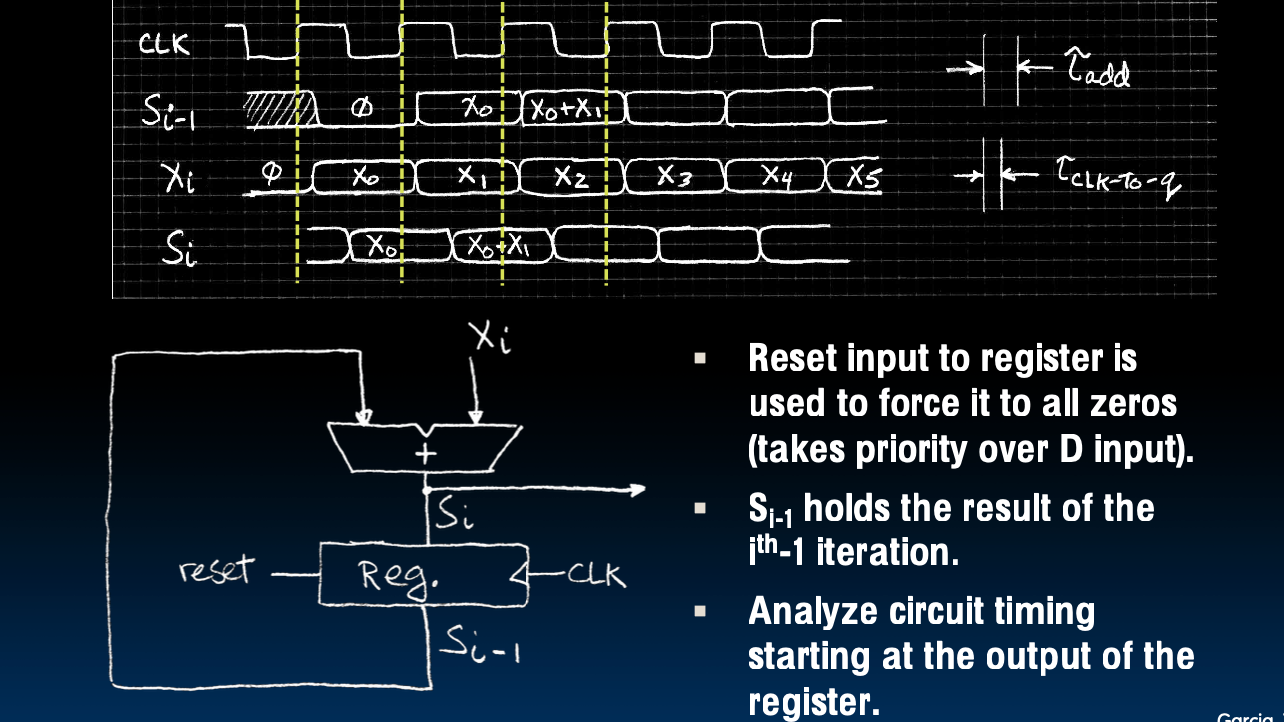
在上图中，时钟信号（CLK）、输入数据（\( X_i \)）、当前累加值（\( S_i \)）和前一轮累加值（\( S_{i-1} \)）的波形展示了在每个时钟周期内的数据传输过程。

Accumulator Revisited (proper timing 2/2)

累加器的正确时序（2/2）

复位信号：复位信号的波形图展示了在复位过程中寄存器如何被清零。
数据到达时间：在实际应用中，\( X \) 可能不会与 \( S_{i-1} \) 同时到达加法器。
暂时错误：\( S_i \) 暂时可能是错误的，但寄存器总能捕获正确的值。
稳定性：在良好的电路设计中，不稳定性不会发生在时钟的上升沿。

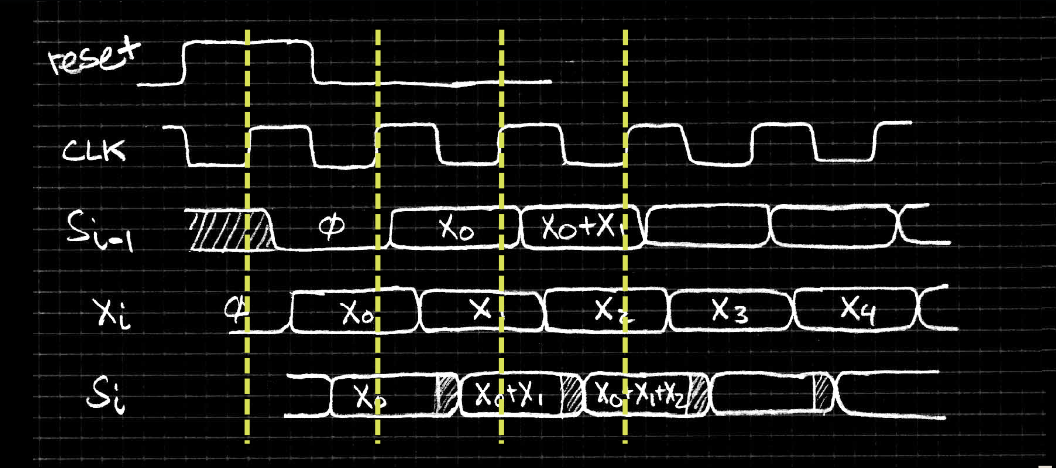
通过波形图，我们可以看到每个时钟周期内，数据 \( X_i \) 如何与前一轮累加值 \( S_{i-1} \) 一起被加法器处理，得到当前的累加值 \( S_i \)，并在下一周期内稳定输出。

这部分内容详细展示了累加器在时序电路中的工作原理，通过复位信号和时钟信号的控制，实现数据的正确累加和输出。

Pipelining for Performance

Maximum Clock Frequency

最大时钟频率

问题：这个电路的最大时钟频率是多少？（提示：频率 = 1 / 周期）
关键点：时钟周期是由组合逻辑和寄存器的延迟决定的。
公式：最大延迟 = 时钟到Q延迟（CLK-to-Q Delay）+ 组合逻辑延迟（CL Delay）+ 设置时间（Setup Time）。

CLK-to-Q Delay：从时钟边沿到寄存器输出变化所需的时间。

组合逻辑延迟：信号通过组合逻辑门所需的时间。

Setup Time：输入信号在时钟边沿之前必须保持稳定的时间。

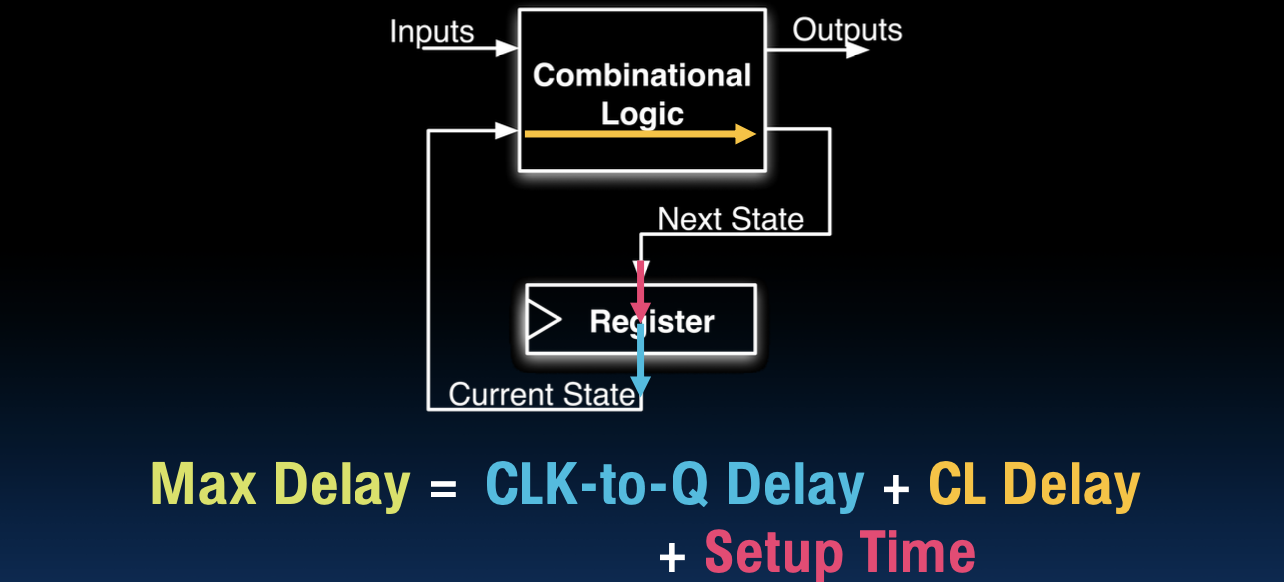
通过图示可以看到，输入信号通过组合逻辑后进入寄存器，然后产生下一状态输出。在此过程中，时钟到Q的延迟、组合逻辑的延迟和设定时间共同决定了最大时钟频率。

Pipelining to improve performance (1/2)

通过流水线提高性能（1/2）

流水线是一种通过在不同阶段之间插入寄存器来分割计算过程的方法。这允许每个阶段在每个时钟周期内处理一部分数据，从而实现并行处理，增加了每秒输出的数量。时间图展示了如何在不同阶段之间移动数据，每个阶段在一个时钟周期内完成其处理任务。

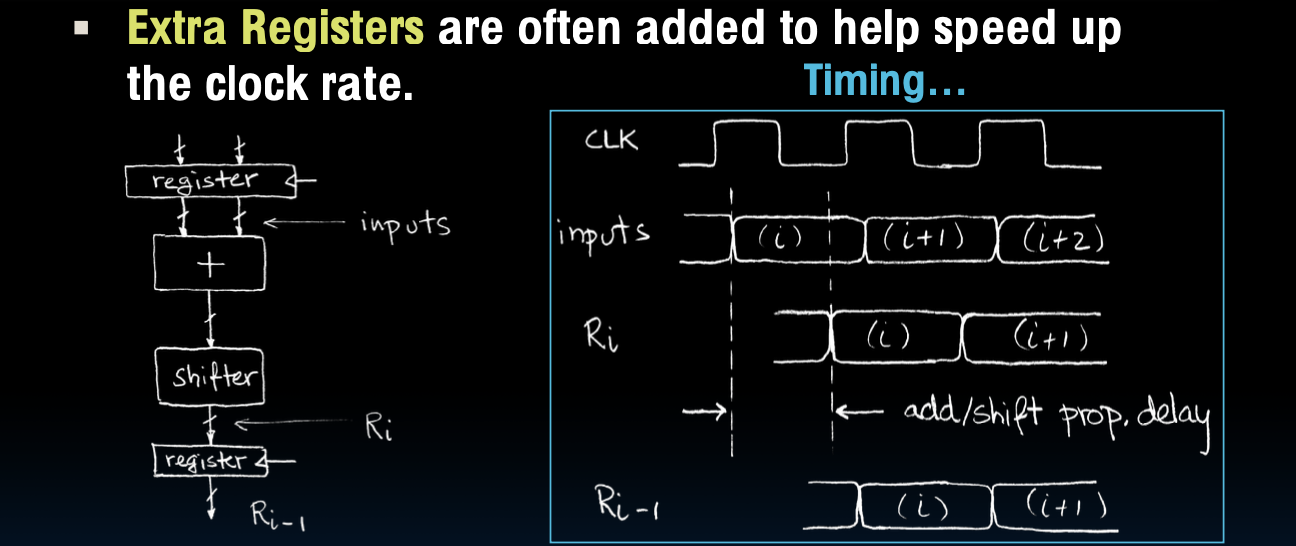
额外寄存器：通常会增加额外的寄存器来帮助加速时钟速率。
注意：从输入到输出有一个时钟周期的延迟。
时钟周期限制：时钟周期受加法器/移位器传播延迟的限制。

在这部分内容中，时序图展示了在时钟周期内数据从输入到输出的传播过程。通过在不同的计算阶段之间增加额外的寄存器，可以将复杂的计算分解为多个阶段，每个阶段在一个时钟周期内完成，从而提高整体电路的性能。

通过增加流水线阶段，可以将复杂计算分解为多个简单的步骤，每个步骤在一个时钟周期内完成。
这样可以显著提高电路的时钟频率和整体性能。
需要注意的是，流水线阶段之间的寄存器增加了时序复杂度，但总体上提高了数据处理速度。

图示展示了通过插入多个寄存器，将复杂计算过程分解为多个阶段。每个阶段在一个时钟周期内完成，从而允许更高的时钟频率，增加每秒钟的输出数量。这种方法可以显著提升系统的性能。

寄存器的作用

寄存器在数字电路中充当了临时存储器的角色，可以在每个时钟周期捕获和保持数据。将寄存器插入组合逻辑电路的关键位置，可以将整个电路分割成多个阶段，每个阶段在一个时钟周期内完成其任务。这样，每个寄存器在时钟周期内捕获其输入，并在下一个时钟周期提供其输出，从而实现阶段间的数据传递。

原理解释

分割逻辑路径：

在没有寄存器的电路中，信号必须穿过所有组合逻辑门，然后才到达输出。这意味着所有逻辑门的总延迟决定了电路的时钟周期。

当在适当的位置添加寄存器后，逻辑路径被分割成多个阶段。每个阶段的逻辑门延迟相对较小，因为它们只需要处理一部分数据。这些阶段可以在不同的时钟周期内独立运行。

寄存器的捕获与保持：

寄存器在时钟的上升沿或下降沿捕获输入数据，并在整个时钟周期内保持这个数据，直到下一个时钟周期。这使得每个阶段的输出都能在下一个时钟周期内作为下一个阶段的输入。

通过这种方式，每个阶段的逻辑门只需要在一个时钟周期内完成其任务，而不需要等到整个逻辑路径上的所有门都完成工作。

并行处理：

当一个阶段在处理当前数据时，前一个阶段已经开始处理新的数据。这样，可以实现流水线并行处理，从而提高整个电路的吞吐量。

例如，假设有三个阶段A、B和C。第一时钟周期，阶段A处理数据X1，第二时钟周期，阶段A处理数据X2，同时阶段B处理数据X1，依此类推。

提高时钟频率：

由于每个阶段的逻辑延迟较短，因此整个电路的时钟周期可以缩短，从而提高时钟频率。这意味着电路可以在更短的时间内完成更多的计算任务，提高了整体性能。

总结

通过在组合逻辑电路中插入寄存器，可以将长的逻辑路径分割成多个短的逻辑路径，每个路径在一个时钟周期内完成其任务。寄存器捕获和保持数据，使得每个阶段可以并行处理不同的数据，从而提高了电路的时钟频率和吞吐量。这种设计方法称为流水线，它是现代处理器和数字系统中常用的技术，用于提高性能和效率。

Recap of Timing Terms

时序术语回顾

Clock (CLK)：稳定的方波信号，用于同步系统。
Setup Time：输入信号在时钟上升沿之前必须稳定的时间。
Hold Time：输入信号在时钟上升沿之后必须保持稳定的时间。
“CLK-to-Q” Delay：从时钟上升沿开始计算，输出变化所需的时间。
Flip-flop：在每个时钟上升沿采样一个比特状态（正沿触发）。
Register：在时钟上升沿或LOAD信号上升沿采样多个比特状态（正沿触发）。

这些术语对于理解时序电路的工作原理至关重要。时钟信号用于同步系统中的所有操作，设定时间和保持时间确保信号在时钟边沿前后保持稳定，而“CLK-to-Q”延迟则描述了时钟边沿到输出变化之间的时间。触发器和寄存器是存储和传输数据的基本组件，确保数据在时钟周期内正确传递。

Finite State Machines (FSM) Introduction

有限状态机（FSM）简介

FSM 的基本概念：有限状态机（Finite State Machine，FSM）是一种抽象机器，用于在一组有限的状态之间进行转换。它的基本思想是通过输入信号的变化来引发状态的变化，并根据当前状态和输入信号决定输出。
状态转换图：FSM 的功能可以用“状态转换图”表示，如图所示，状态1可以根据输入/输出转换到状态2或状态3。
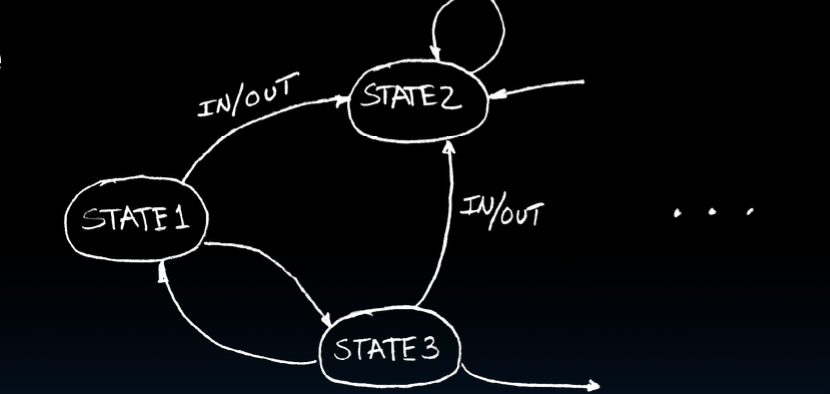
硬件实现：通过组合逻辑和寄存器，任何 FSM 都可以在硬件中实现。组合逻辑用于计算状态转换和输出逻辑，而寄存器用于存储当前状态。通过时钟信号控制，FSM 可以在每个时钟周期更新状态，实现预定的状态转换和输出。

Finite State Machine Example: 3 ones…

有限状态机示例：检测连续的3个1

目标：设计一个 FSM 来检测输入中连续出现的3个1。
状态转换：假设状态转换由时钟控制。在每个时钟周期，机器检查输入，并移动到新状态并产生新的输出。

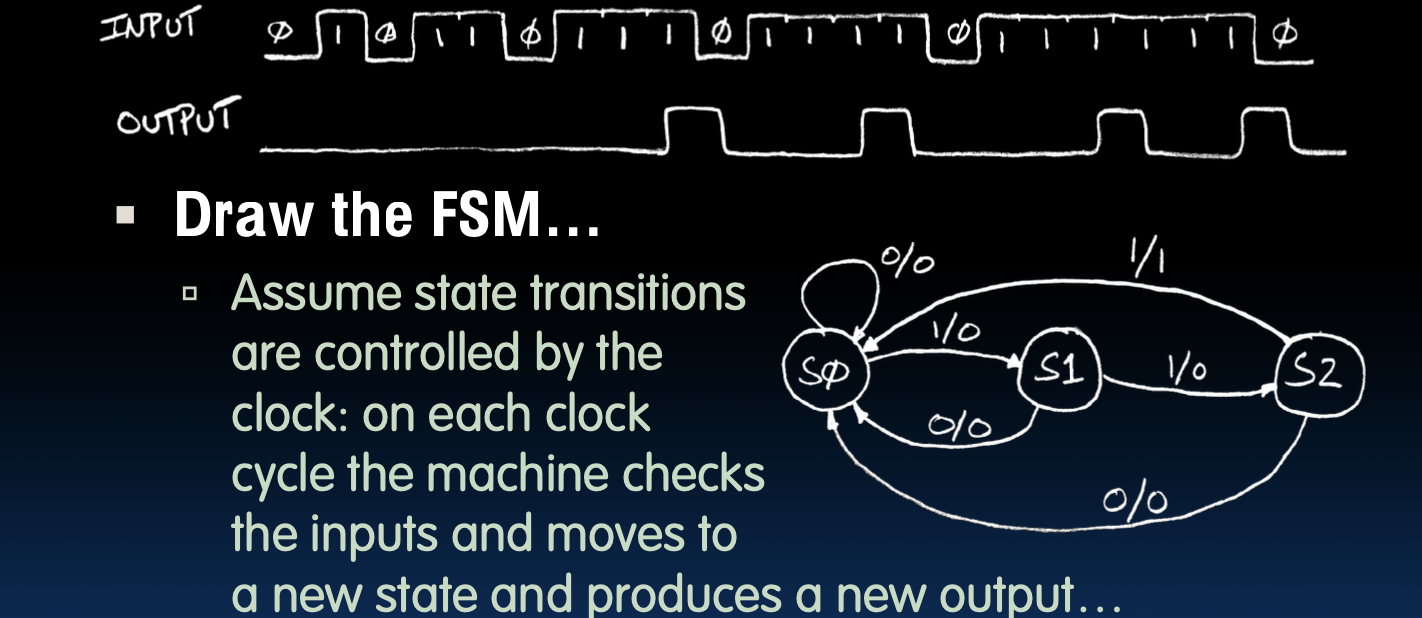
图示展示了一个简单的 FSM，用于检测连续的三个1，初始状态是SP。

SP（初始状态）：如果输入信号为0，则保持在SP状态；如果输入信号为1，则转到S1状态。
S1：如果下一个输入信号为0，则返回SP状态；如果输入信号为1，则转到S2状态。
S2：如果下一个输入信号为0，则返回SP状态；如果输入信号为1，则转到S3状态。
S3：检测到三个连续的1，输出信号为1；如果输入信号为0，则返回SP状态。

Hardware Implementation of FSM

FSM 的硬件实现

寄存器的作用：需要一个寄存器来保存状态机当前所处的状态的表示。对于每个状态，使用一个独特的位模式。
组合逻辑电路：使用组合逻辑电路来实现从输入和当前状态（PS）到下一个状态（NS）和输出的函数映射。

下图展示了组合逻辑电路和寄存器的结合方式：寄存器存储当前状态，组合逻辑电路根据当前状态和输入决定下一个状态和输出。

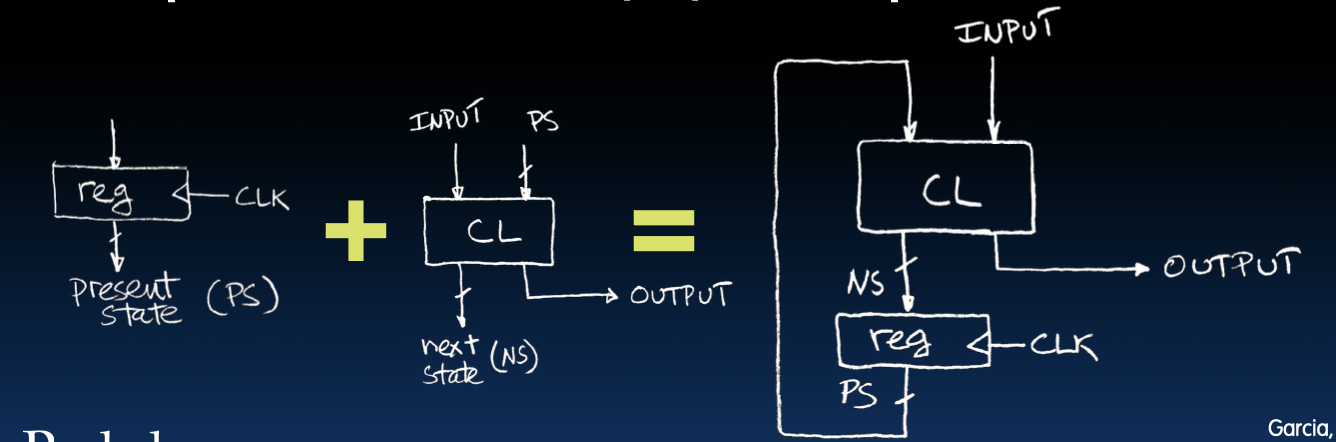
Hardware for FSM: Combinational Logic

FSM 的硬件：组合逻辑

详细实现讨论：下一次讲座将讨论详细实现，现在先看功能规格，真值表形式。

图示展示了 FSM 的真值表形式，输入和当前状态决定下一个状态和输出。例如，当当前状态是00，输入是1时，下一个状态是01，输出是0。

General Model for Synchronous Systems

同步系统的一般模型

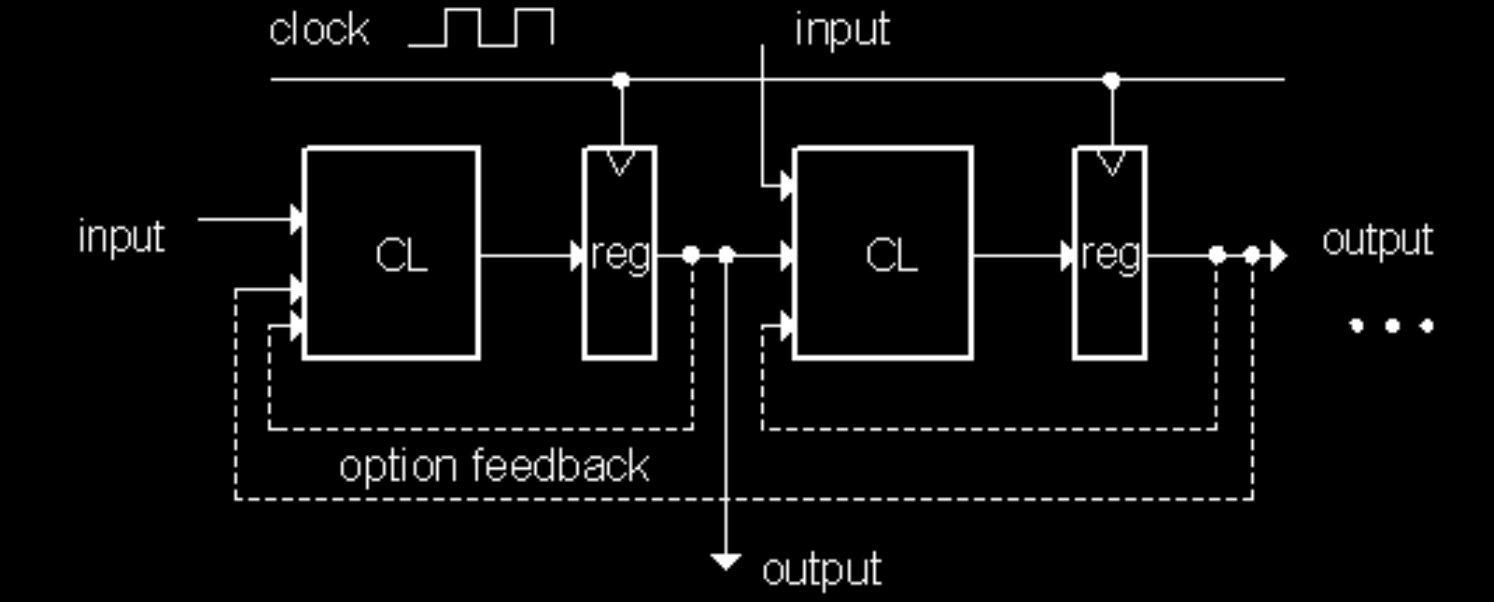
组合逻辑块集合：由寄存器分隔的组合逻辑块集合。
寄存器和组合逻辑块的排列：寄存器可以背靠背排列，组合逻辑块也可以背靠背排列。
反馈：反馈是可选的。
时钟信号：时钟信号仅连接到寄存器的时钟输入。

图示展示了同步系统的一般模型，寄存器在组合逻辑块之间起到分隔作用，时钟信号同步整个系统的操作。

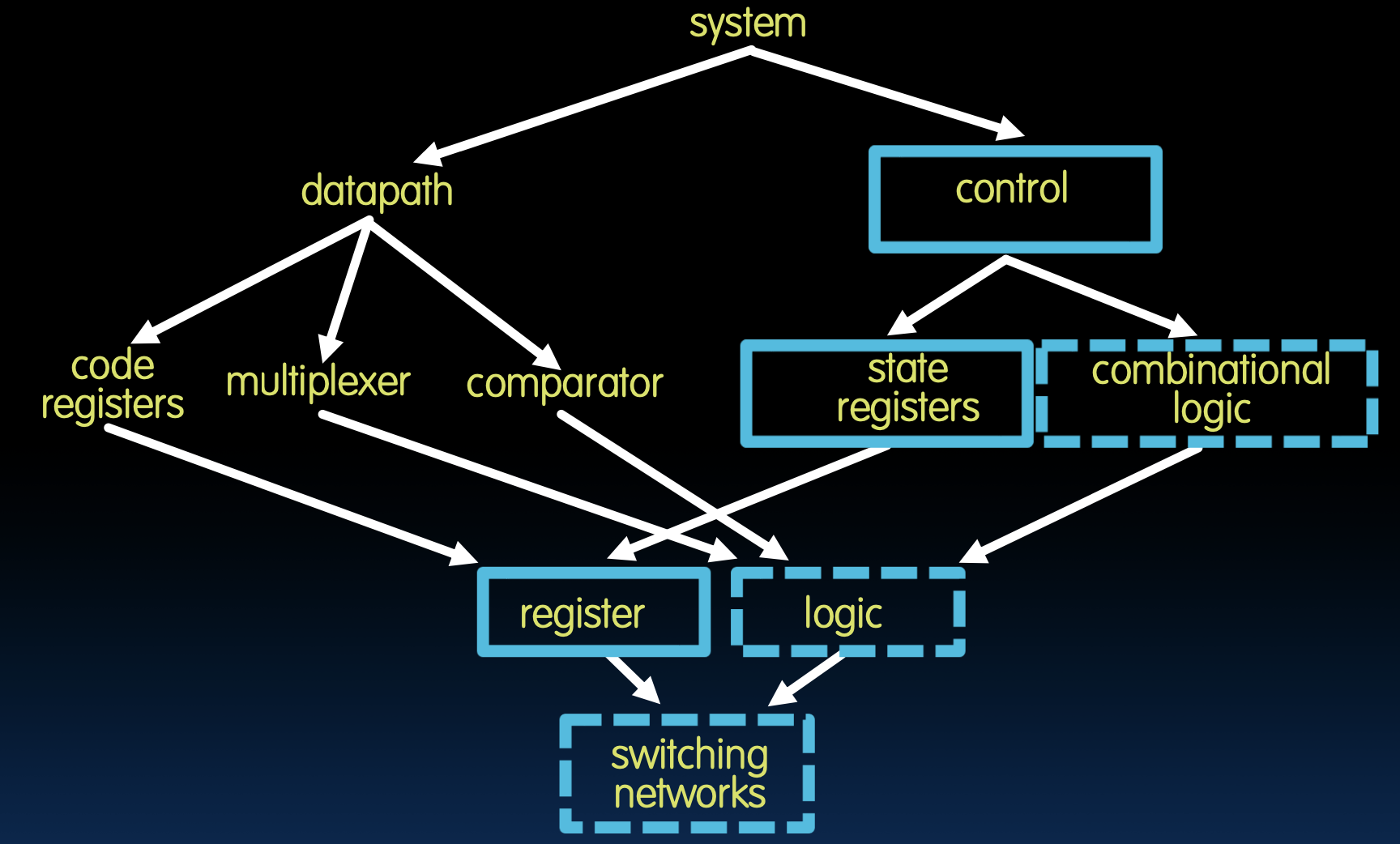
Design Hierarchy

设计层次结构

系统（system）：最顶层，包含所有的子模块。
数据路径（datapath）：处理数据流的路径，包括寄存器、比较器和多路复用器。
控制（control）：负责控制数据路径的操作。
状态寄存器（state registers）：保存当前状态的信息。
组合逻辑（combinational logic）：实现状态之间的转换逻辑。
寄存器（register）：存储数据和状态。
逻辑（logic）：具体的逻辑实现。
开关网络（switching networks）：用于控制信号的传输。

此图展示了系统设计的分层结构，各个子模块如何相互连接和协作。

设计层次（Design Hierarchy）

这张图展示了一个系统设计的层次结构，描述了从顶层系统设计到底层逻辑和寄存器的分解过程。以下是图中各部分的详细解释：

系统 (System)

最高层次：表示整个系统的设计，它包括所有的组件和子系统。

数据通路 (Datapath)

数据处理路径：负责处理数据流动，通常包括算术运算单元（ALU）、寄存器、数据总线等。

组件：多路复用器（multiplexer）、比较器（comparator）和代码寄存器（code registers）等。

控制 (Control)

控制单元：负责管理数据流动的控制信号，确保各个部分按照预定的方式工作。

状态寄存器 (State Registers)：存储当前状态信息，并与组合逻辑 (Combinational Logic) 一起决定下一个状态。

组合逻辑 (Combinational Logic)

逻辑运算：执行不需要存储状态的逻辑运算，输出仅仅取决于当前输入。

寄存器 (Register)

存储单元：存储数据和状态信息，用于保持数据的一致性和顺序性。

功能：与组合逻辑配合，实现状态转移和数据处理。

开关网络 (Switching Networks)

And In Conclusion…

总结…

状态元素的作用：
- 构建内存。
- 控制状态元素和组合逻辑之间信息流的流动。
D触发器用于构建寄存器：D触发器是一种基本的存储元件，用于保存单个位的数据。
时钟信号的作用：时钟信号告诉D触发器何时改变状态，设置时间和保持时间非常重要。
流水线化长延迟的组合逻辑以加快时钟速度：通过流水线化，可以将长延迟的组合逻辑分解为多个阶段，每个阶段的计算结果存储在寄存器中，从而提高整体系统的时钟频率。
有限状态机（FSM）极其有用：FSM用于实现复杂的控制逻辑，将在更高级的课程（如151A、152、164、172等）中再次看到。

通过这些概念和技术，可以设计和实现高效的同步数字系统，确保系统在每个时钟周期内正确地执行其功能。