Lecture 28: Flynn Taxonomy, SIMD

Parallelism

并行计算概述

并行计算是指在多个计算资源上同时执行多个计算任务，以提高计算性能和效率。图中展示了并行计算在软件和硬件中的不同层次的实现和应用。

软件层次的并行

• 并行请求：
  • 分配给计算机，例如，搜索“Cats”。
  • 多个独立的请求可以同时被处理，以提高系统的响应能力。
• 并行线程：
  • 分配给核心，例如，执行查找、广告等任务。
  • 多个线程可以在一个或多个处理器核心上同时运行，以提高计算性能。
• 并行指令：
  • 一次执行多条指令，例如，5条流水线指令。
  • 处理器可以在同一时刻执行多条指令，利用流水线技术提高指令执行效率。
• 并行数据：（本节内容）
  • 一次处理多个数据项，例如，一次加法操作处理4对数据。
  • 通过单指令多数据（SIMD）技术，可以在一次指令中处理多个数据项，提高数据处理速度。

硬件层次的并行

• 仓库级计算机：
  • 大规模的数据中心，包含成千上万的服务器，通过并行处理大量请求来实现高性能计算。
• 核心和多核心处理器：
  • 单个处理器核心和多核心处理器，通过多核心并行执行任务，提高计算能力。
• 内存和缓存：
  • 内存和缓存的并行访问，可以提高数据访问速度，减少延迟。
• 执行单元和功能块：
  • 处理器内部的执行单元和功能块可以并行工作，执行不同的计算任务。
• 逻辑门：
  • 硬件描述中，所有逻辑门可以并行工作，以实现快速的信号处理和数据传输。

并行计算的优势

通过在软件和硬件层次实现并行计算，可以显著提高计算性能，减少执行时间，增强系统的响应能力。在现代计算机系统中，并行计算是实现高性能和高效率的关键技术。

---

视角…

引用

“真正的问题是程序员花了太多时间在错误的地方和错误的时间关注效率；过早的优化是所有问题的根源（或至少是大多数问题的根源）。” ——唐纳德·克努斯，《计算机程序设计艺术》

解释

著名计算机科学家唐纳德·克努斯指出，程序员往往在错误的地方和错误的时间过于关注效率，而过早的优化是所有问题的根源（或至少是大多数问题的根源）。这句话提醒我们，在编写程序时，不应该过早关注优化，而是应该首先确保程序的正确性和可读性，然后在需要时进行优化。

通过并行计算，可以在适当的时间和地方进行优化，从而实现高性能计算，而不需要在编程的早期阶段过于关注细节优化。这种方式不仅可以提高程序的效率，还可以减少编程过程中的复杂性和错误。

---

Flynn Taxonomy

弗林分类法

软件与硬件并行性

软件与硬件并行性比较

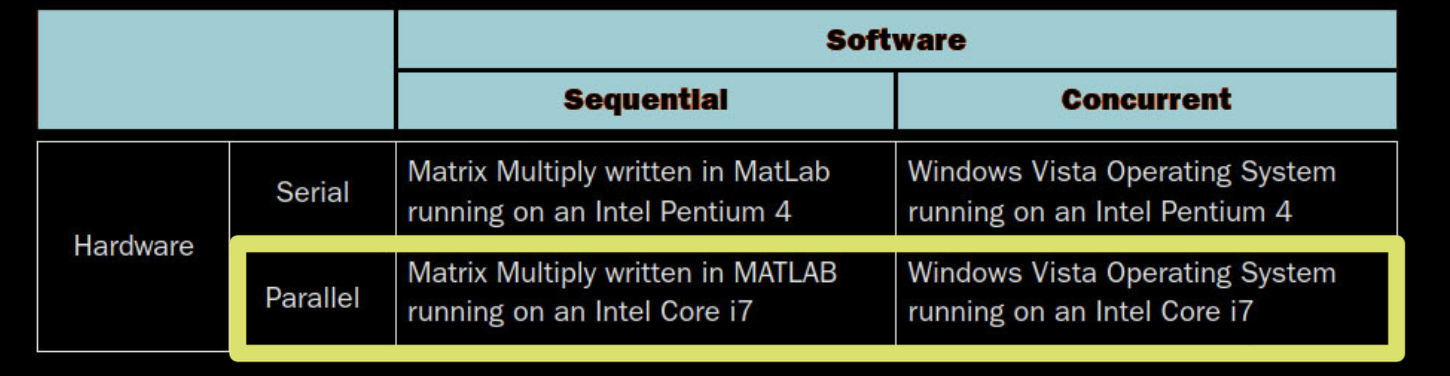
选择硬件和软件并行性是独立的

• 并行软件也可以在串行硬件上运行
• 串行软件也可以在并行硬件上运行
• Flynn分类法是用于并行硬件的

在计算系统中，硬件和软件的并行性是可以独立选择的。这意味着即使硬件支持并行处理，软件也可以是串行的，反之亦然。Flynn分类法根据指令和数据流的数量将计算机体系结构分为四类：单指令单数据流（SISD）、单指令多数据流（SIMD）、多指令单数据流（MISD）和多指令多数据流（MIMD）。

单指令/单数据流（SISD）

SISD结构

• 序列计算机，不利用指令或数据流中的任何并行性
• SISD架构的例子是传统的单处理器机器

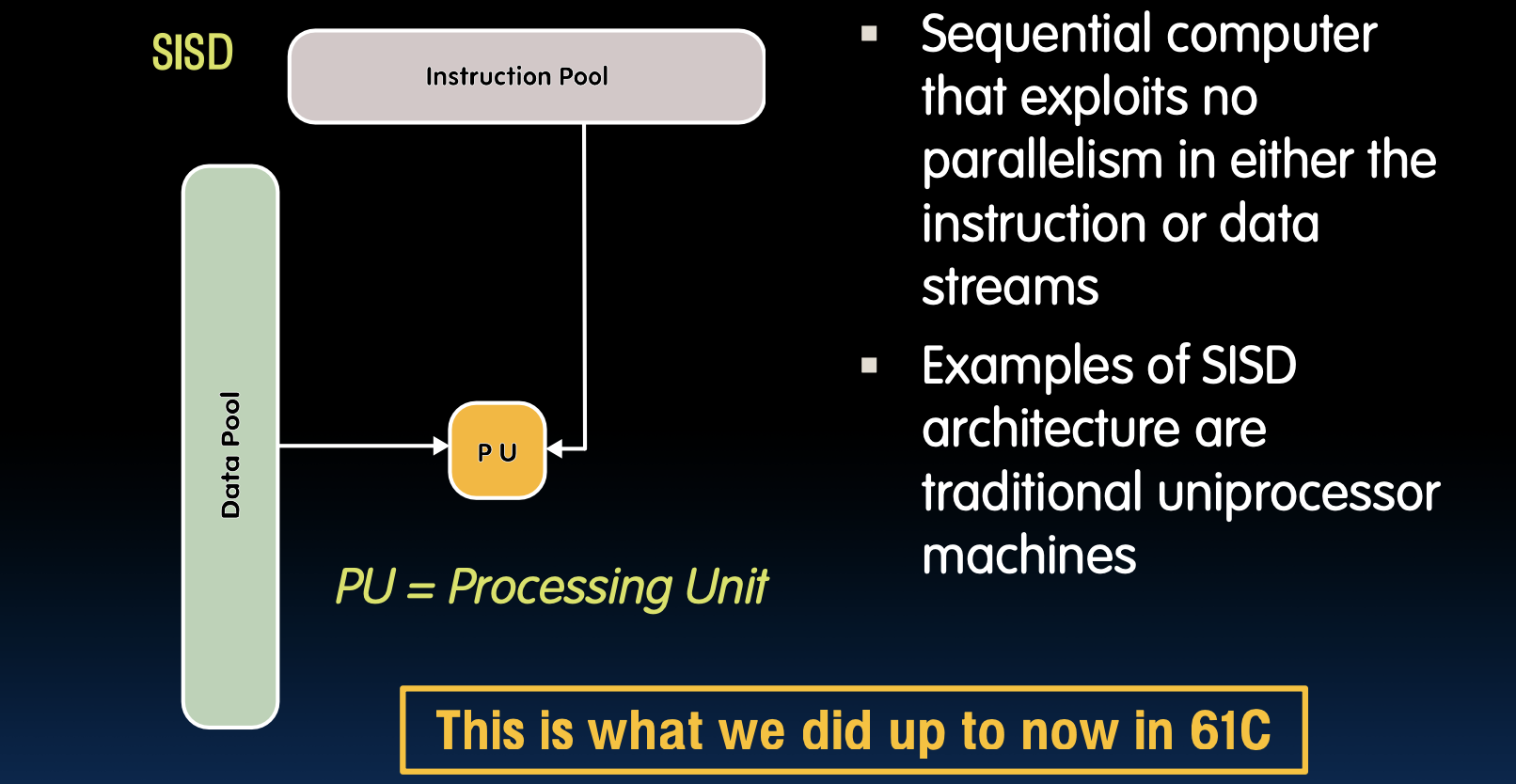
SISD架构是最基本的计算机结构，其中每个时钟周期内处理器执行一个指令并操作一个数据流。这种架构常见于早期的计算机系统和一些嵌入式系统。它的特点是简单，但在处理复杂任务和大规模数据时效率较低，因为无法利用并行性来加速计算。

单指令/多数据流（SIMD）

SIMD结构

• 计算机应用单个指令流到多个数据流，适用于可自然并行化的操作（如SIMD指令扩展或图形处理单元）

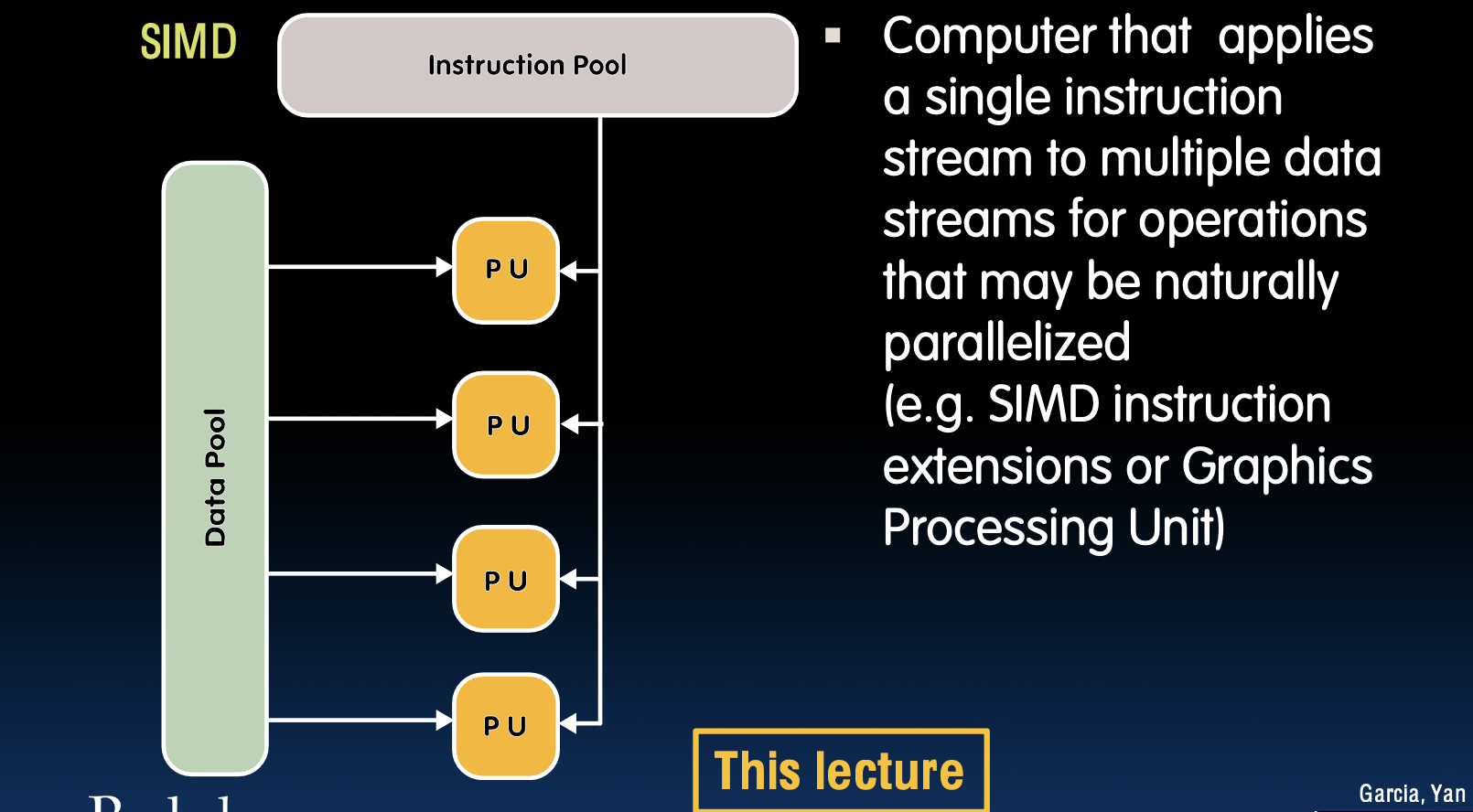
在SIMD架构中，一个指令控制多个处理单元同时操作不同的数据。这种架构特别适用于数据并行任务，例如图形处理、科学计算和多媒体应用。SIMD能够显著提高处理速度，因为同一操作可以在多个数据元素上同时执行。现代处理器（如GPU）通常采用SIMD架构，以在图像处理和机器学习等应用中实现高效并行计算。

多指令/多数据流（MIMD）

MIMD结构

• 多个自主处理器同时对不同数据执行不同指令
• MIMD架构包括多核处理器和仓库规模计算机

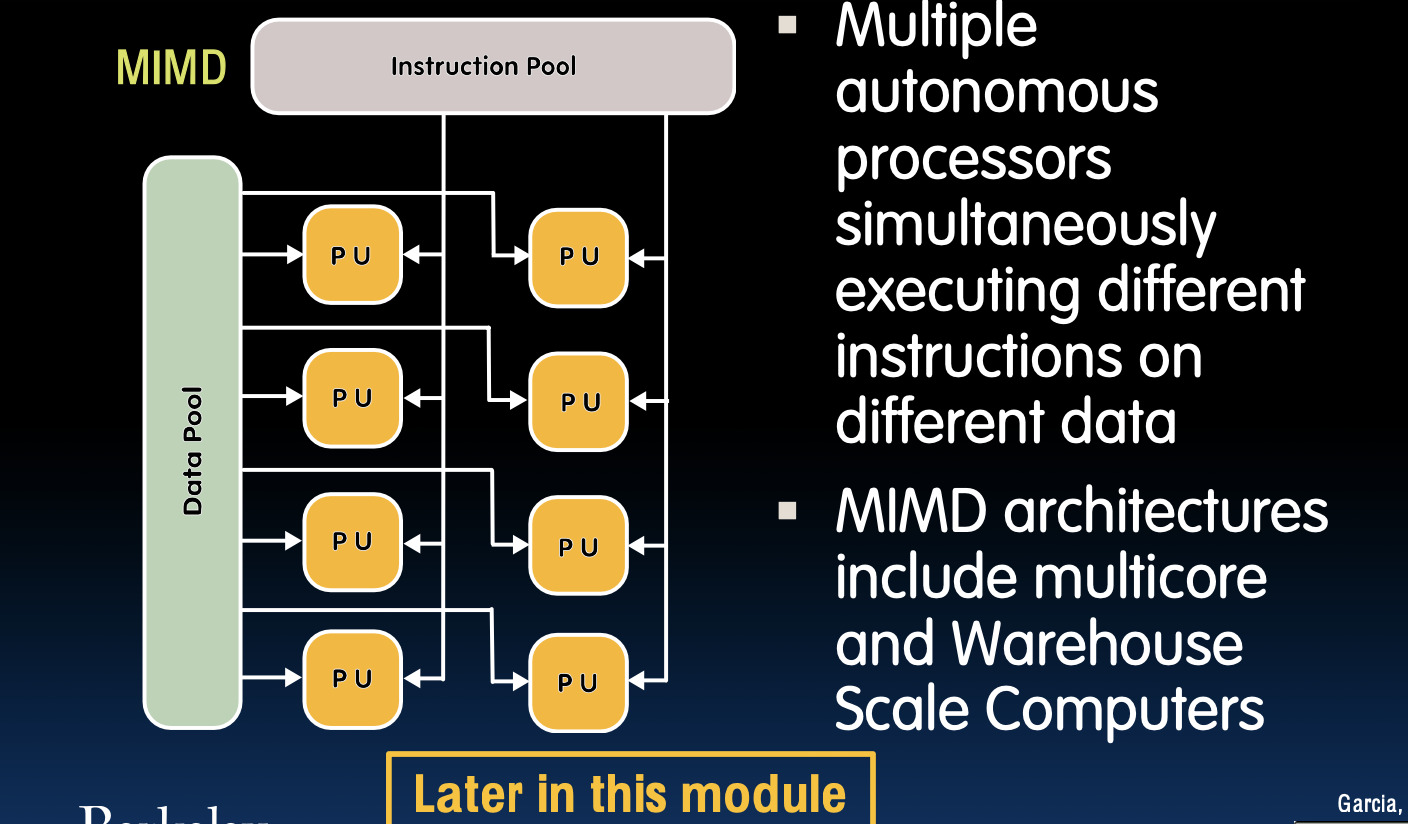
在MIMD架构中，每个处理器都有自己的指令和数据流，可以独立执行不同的任务。这种架构非常灵活，适用于需要同时处理多个独立任务的应用场景，如大型服务器和高性能计算机。在多核处理器中，每个核心都可以被视为一个MIMD处理器，能够并行处理不同的线程或进程，从而大幅提高计算效率。

多指令/单数据流（MISD）

MISD结构

• 利用多个指令流对单个数据流进行操作，适用于自然并行的数据操作（如某些类型的阵列处理器）
• MISD架构不再常见，主要具有历史意义

MISD架构在实际应用中很少见，因为它的适用范围非常有限。通常，只有在需要对单个数据流进行多种不同处理的情况下，才会考虑使用MISD架构。例如，在一些特定的信号处理和故障检测系统中，可能会使用MISD架构来实现数据的多次不同处理。然而，由于这种需求并不普遍，因此MISD在现代计算机架构中几乎没有应用。

Flynn分类法

Flynn分类法简介

Flynn分类法根据指令流和数据流的数量将计算机体系结构分为四类：

• SISD（单指令单数据流）：如Intel Pentium 4
• SIMD（单指令多数据流）：如x86的SSE指令
• MISD（多指令单数据流）：目前没有实际例子
• MIMD（多指令多数据流）：如Intel Xeon e5345（Clovertown）

Flynn分类法是分析和理解计算机架构的一种经典方法。SISD是最基本的计算模式，适用于单处理器系统；SIMD适用于数据并行处理，常见于图形处理单元（GPU）和多媒体应用；MISD虽然理论上存在，但在实际中应用很少；MIMD是现代多处理器系统的基础，广泛应用于服务器、高性能计算和分布式系统中。通过这种分类，能够更好地理解不同计算架构的特点和适用场景。

SIMD Architectures

SIMD 架构

数据级并行（DLP）

• 数据级并行（DLP）：在多个数据流上执行一个操作

• 示例：用系数向量乘以数据向量（例如，在滤波中）

  y[i] := c[i] × x[i], 0 ≤ i < n
  

数据级并行（DLP）是指对一组数据进行相同操作的一种并行计算方法。在SIMD架构中，单个指令可以同时作用于多个数据元素。例如，向量化操作可以在单个时钟周期内对整个向量进行计算，从而大大提高了计算效率。许多编程语言和编译器都支持这种并行计算模式，使得开发者可以更容易地利用硬件的并行计算能力。

SIMD架构的性能提升主要来自于以下几个方面：

1. 指令获取和解码：因为所有操作只需一条指令，所以减少了指令获取和解码的开销。
2. 操作独立性：每个数据元素的操作都是独立的，可以在多个处理单元上并行执行，避免了数据依赖带来的等待时间。
3. 流水线和并发访问：通过流水线技术，可以在不同阶段并行处理多个操作，同时内存访问也可以并行进行，从而减少了数据传输的瓶颈。

首个SIMD扩展：MIT林肯实验室TX-2，1957年

扩展讲解：在1957年，MIT林肯实验室开发了TX-2计算机，这是早期的SIMD计算架构之一。TX-2能够同时执行多个算术元素的操作，通过将指令控制多个独立的算术单元来实现并行计算。图中展示了不同位宽的算术元素结构，说明了如何通过不同的耦合方式实现并行计算。这个设计为后来的SIMD架构奠定了基础，使得在现代计算中能够更高效地处理大量数据。

Advanced Digital Media Boost

提高性能：Intel的SIMD指令

• 获取一条指令，完成多条指令的工作：利用单条指令在多个数据上执行操作，以提高处理效率。
• MMX（MultiMedia eXtension）：Pentium II处理器系列引入的多媒体扩展。
• SSE（Streaming SIMD Extension）：从Pentium III及之后的处理器开始引入的流SIMD扩展。

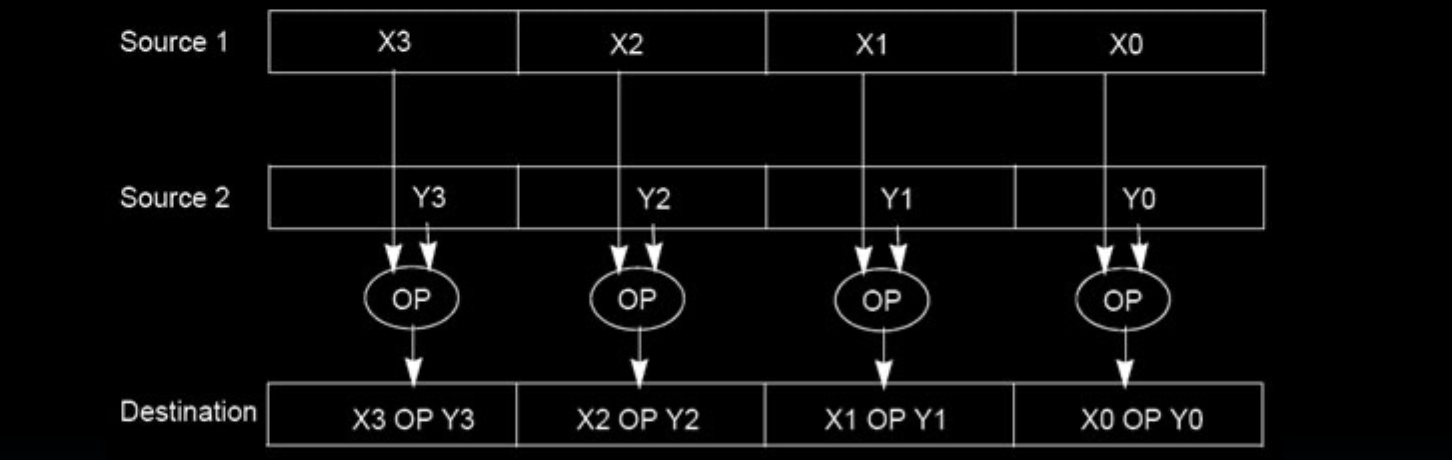
Intel的SIMD指令集通过利用数据并行性来显著提高计算性能。MMX指令集是最早的多媒体扩展，专注于多媒体应用的加速。之后的SSE指令集进一步扩展了SIMD能力，支持更广泛的应用，包括图像处理、科学计算等。通过在单个时钟周期内执行多次操作，SIMD指令能够大大减少计算时间。

Intel x86 SIMD Evolution

从MMX到现代SIMD指令集

• 开始于多媒体扩展（MMX）
  • 每隔几年引入新指令
  • 新的更宽的寄存器
  • 更多的并行性

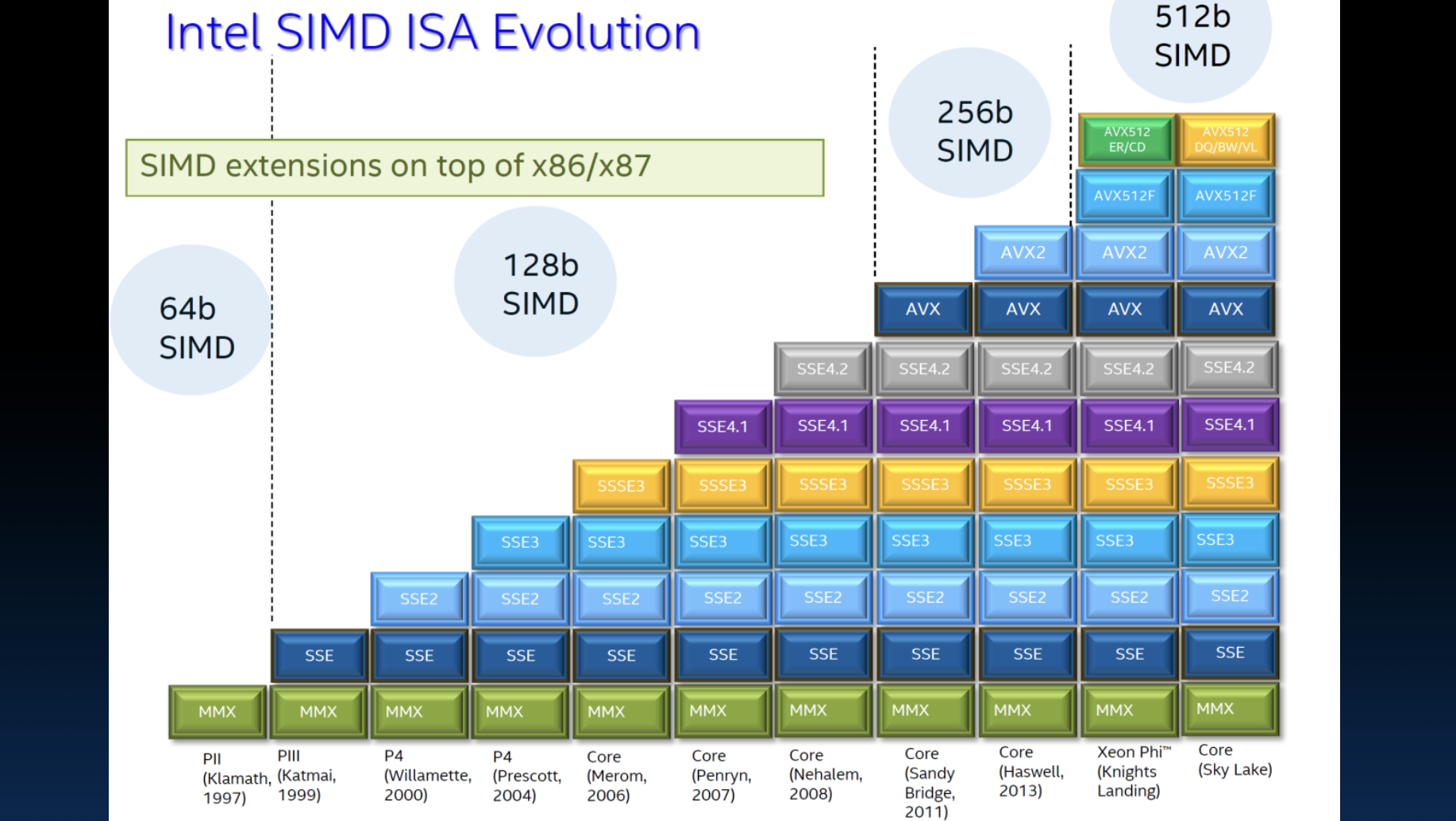
Intel的SIMD指令集从最初的MMX发展到现代的AVX，经历了多次演进。每次更新不仅增加了新的指令，还扩展了寄存器的宽度，从64位扩展到128位、256位甚至512位。这些扩展使得处理器能够在单个时钟周期内处理更多的数据，从而显著提高了并行计算的效率。

XMM Registers in SSE

SSE中的XMM寄存器

• 架构扩展：增加了八个128位数据寄存器
  • 64位地址架构：可用作16个64位寄存器（XMM8 - XMM15）
  • 例如，128位打包单精度浮点数据类型（双字），允许同时执行四个单精度操作

SSE指令集引入了XMM寄存器，这些128位寄存器使处理器能够同时执行多次浮点运算。通过将多个浮点数打包到一个寄存器中，处理器可以在单个时钟周期内执行多个操作。这种并行处理方式大大提高了浮点计算的性能，特别是在科学计算和多媒体应用中。随着架构的进一步发展，更多的XMM寄存器被引入，提供了更大的灵活性和更高的计算能力。

Intel Architecture SSE2 + 128-Bit SIMD Data Types

基本的128位打包SIMD数据类型

• Packed Bytes: 16个字节（16/128位）
• Packed Words: 8个字（8/128位）
• Packed Doublewords: 4个双字（4/128位）
• Packed Quadwords: 2个四字（2/128位）

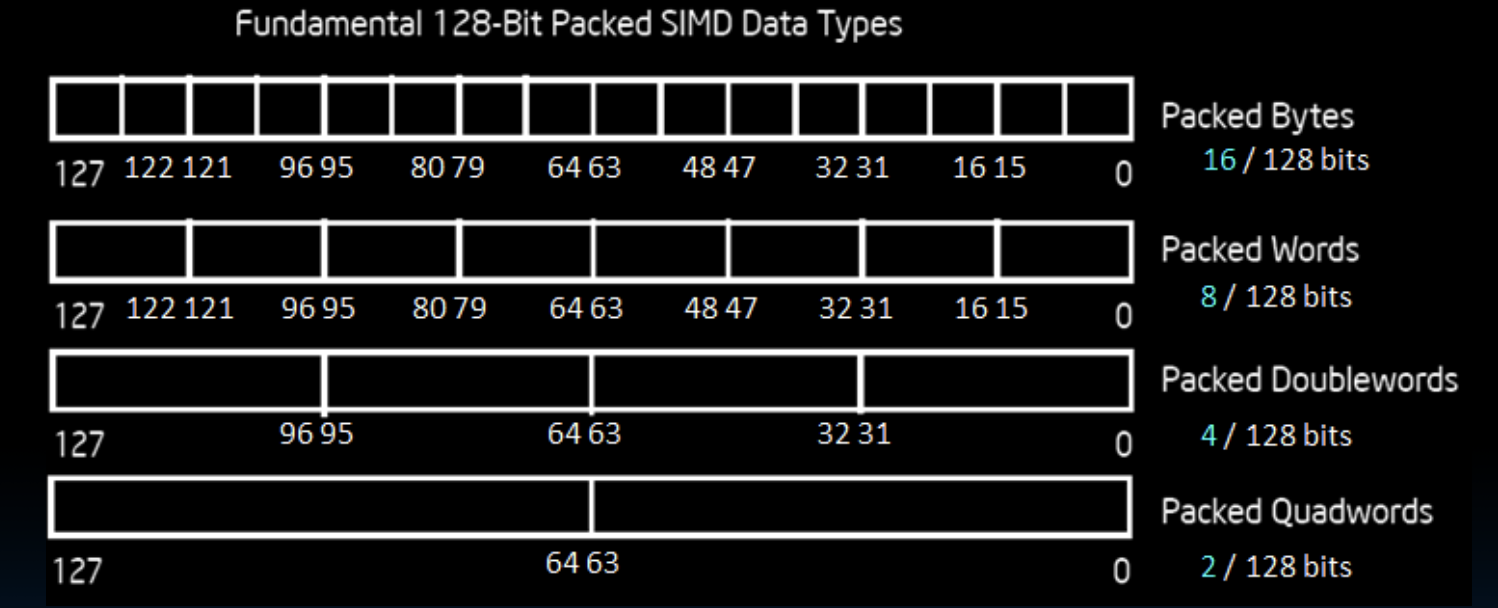
在SSE2指令集中，Intel架构提供了多种打包数据类型，用于在128位寄存器内处理多个数据元素。例如，Packed Bytes允许在一个寄存器中处理16个8位的字节，Packed Words允许处理8个16位的字，Packed Doublewords允许处理4个32位的双字，而Packed Quadwords则允许处理2个64位的四字。这些打包数据类型使得SIMD能够在单个指令周期内并行处理多个数据，提高了数据处理的效率。

注意事项

• 在Intel架构中（与RISC V不同），一个字是16位的
  • 单精度浮点数：双字（32位）
  • 双精度浮点数：四字（64位）

Intel架构中定义的字长与RISC V有所不同。在Intel架构中，一个字长为16位，这影响了浮点数的表示方式。单精度浮点数使用32位双字表示，而双精度浮点数则使用64位四字表示。这种定义在使用SIMD指令进行浮点运算时需要特别注意，以确保数据处理的正确性。

SIMD Registers in AVX512

AVX512状态

• Kmask k0..k7
• zmm0..zmm31
• ymm0..ymm15
• xmm0..xmm7

AVX512是Intel架构中新的SIMD扩展，提供了更高的并行计算能力。AVX512指令集增加了更多的寄存器，如zmm寄存器（zmm0到zmm31），每个寄存器宽度为512位，能够处理更多的数据。同时，AVX512还引入了Kmask寄存器（k0到k7），用于条件掩码操作，以提高数据处理的灵活性和效率。与SSE相比，AVX512的寄存器状态增加了8倍，这意味着需要更多的状态来补偿内存带宽，以实现更高的计算性能。

Check Out a Typical Laptop (lscpu)

示例说明：

• 型号: Intel(R) Core(TM) i7-1065G7 CPU @ 1.30GHz
• 标志: sse2, sse3, ssse3, sse4_1, sse4_2, avx, avx2, avx512f, avx512dq, avx512cd, avx512bw, avx512vl

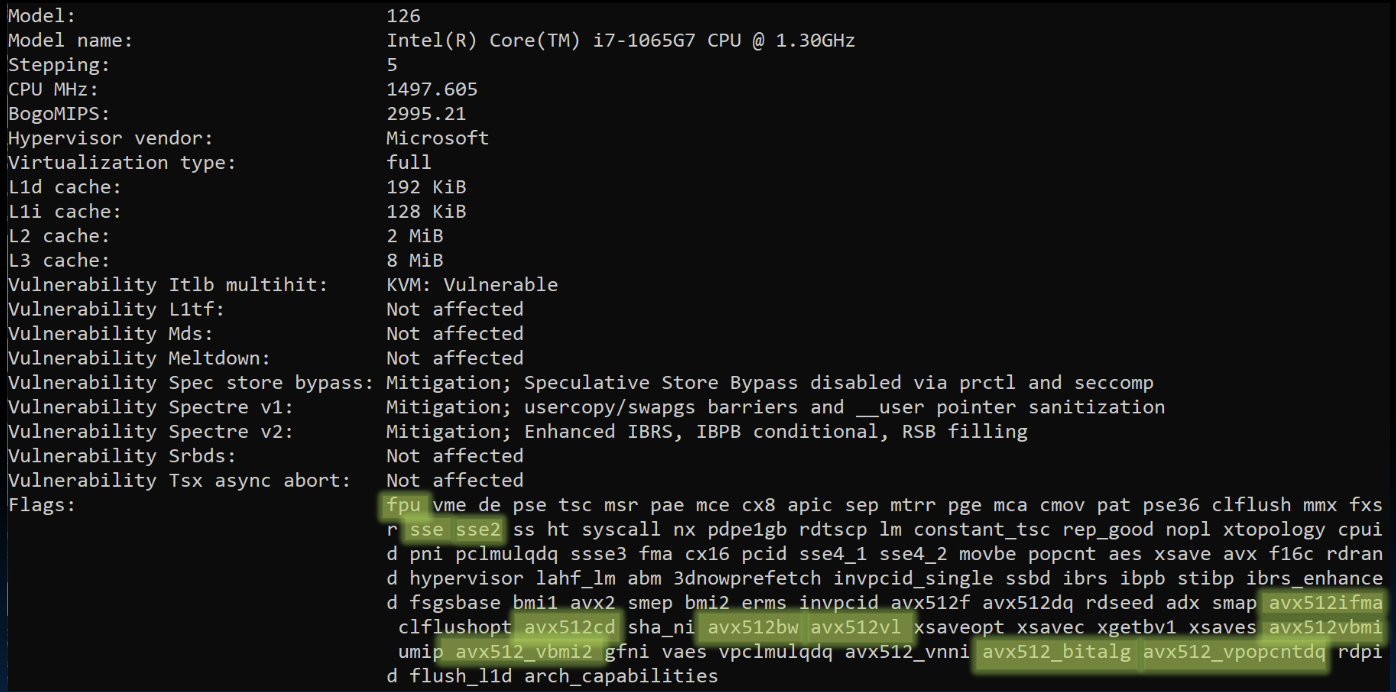
从典型的笔记本电脑配置中可以看到，现代处理器支持多种SIMD指令集扩展，如SSE2、AVX、AVX2和AVX512。这些扩展使得处理器能够在多媒体处理、科学计算和数据分析等应用中提供更高的性能。例如，AVX512扩展提供了更宽的寄存器和更多的指令，能够在单个时钟周期内处理更多的数据，从而显著提高计算效率。通过查看处理器支持的指令集，可以了解其在并行计算中的能力和适用范围。

SIMD Array Processing

Example: SIMD Array Processing

伪代码示例

for each f in array:
    f = sqrt(f)

这段伪代码展示了如何遍历一个数组，并对每个元素计算其平方根。这种方式是最基本的顺序处理，没有使用任何并行化技术。

SISD (Single Instruction Single Data)

for each f in array {
    load f to the floating-point register
    calculate the square root
    write the result from the register to memory
}

SISD架构下，对于数组中的每个元素，处理器需要逐个加载到浮点寄存器中，计算平方根，然后将结果写回内存。这种方式处理每个数据元素需要独立的指令周期，效率较低。

SIMD (Single Instruction Multiple Data)

for every 4 members in array {
    load 4 members to the SSE register
    calculate 4 square roots in one operation
    write the result from the register to memory
}

SIMD架构通过使用SSE寄存器，可以一次性加载多个数据元素（例如4个），并在一个指令周期内同时计算这些元素的平方根。这样显著提高了数据处理的并行度和效率。使用SIMD指令可以大幅减少循环的迭代次数，从而加快处理速度。

Example: Add Single-Precision FP Vectors

示例：添加单精度浮点向量

需要执行的计算

vec_res.x = v1.x + v2.x;
vec_res.y = v1.y + v2.y;
vec_res.z = v1.z + v2.z;
vec_res.w = v1.w + v2.w;

这里展示了将两个四维向量（v1和v2）相加的计算过程，每个维度的结果存储在vec_res中。这是一个典型的向量加法操作，在SIMD架构中可以并行处理多个维度的数据。

SSE 指令序列

movaps address-of-v1, %xmm0
// v1.w | v1.z | v1.y | v1.x -> xmm0
addps address-of-v2, %xmm0
// v1.x+v2.x | v1.y+v2.y | v1.z+v2.z | v1.w+v2.w -> xmm0
movaps %xmm0, address-of-vec_res

以下是使用SSE指令执行上述向量加法操作的步骤：

1. movaps address-of-v1, %xmm0
   • 将内存中的v1加载到XMM寄存器%xmm0中。
   • movaps：从内存到XMM寄存器的移动操作，要求内存对齐且数据是打包的单精度浮点数。
   • 加载结果：%xmm0中现在包含v1.w | v1.z | v1.y | v1.x。
2. addps address-of-v2, %xmm0
   • 将内存中的v2加载到XMM寄存器%xmm0中，并与%xmm0中的v1相加。
   • addps：对打包的单精度浮点数执行加法操作。
   • 加载并相加结果：%xmm0中现在包含v1.w+v2.w | v1.z+v2.z | v1.y+v2.y | v1.x+v2.x。
3. movaps %xmm0, address-of-vec_res
   • 将XMM寄存器%xmm0中的结果存储回内存中的vec_res。
   • movaps：从XMM寄存器到内存的移动操作，要求内存对齐且数据是打包的单精度浮点数。
   • 存储结果：内存地址address-of-vec_res中现在包含vec_res.w | vec_res.z | vec_res.y | vec_res.x。

在SSE指令集中，movaps指令用于将内存中的数据块（例如向量v1）加载到128位的XMM寄存器中。然后，使用addps指令将另一个向量v2加到XMM寄存器中的数据上。这些指令一次性处理多个数据元素，实现了并行计算。最后，movaps指令将计算结果存回内存地址vec_res。

SSE（Streaming SIMD Extensions）指令集提供了强大的并行计算能力，特别适用于处理需要高吞吐量的向量和矩阵计算。在现代处理器中，SSE指令集已被广泛使用，并被更先进的AVX（Advanced Vector Extensions）指令集所扩展，这些扩展提供了更宽的寄存器和更多的并行计算能力。了解并使用这些指令集可以显著提高计算密集型任务的性能。

Intel SSE Intrinsics

内在函数（Intrinsics）

• 内在函数说明：内在函数是将包括SSE指令在内的汇编语言放入C函数和程序中的方法。
  • 使用内在函数，可以间接使用这些指令编程
  • SSE指令和本质之间存在一一对应关系

内在函数（Intrinsics）是一种特殊的编程接口，允许程序员在高层次语言（如C/C++）中直接使用处理器的低级别指令（如SSE指令）。这提供了一种在不编写纯汇编代码的情况下，利用硬件特性优化性能的方法。通过内在函数，开发人员可以更方便地实现数据并行处理，提高计算密集型应用的效率。

• 向量数据类型：__m128d
  • 这是SSE寄存器的数据类型，表示128位的双精度浮点数向量。
• 加载和存储操作
  • __mm_load_pd：加载对齐的打包双精度浮点数
  • __mm_store_pd：存储对齐的打包双精度浮点数
  • 对应的SSE指令：MOVAPD/对齐的打包双精度，MOVAPD/对齐的打包双精度
• 算术操作
  • __mm_add_pd：打包双精度浮点数加法
  • __mm_mul_pd：打包双精度浮点数乘法
  • 对应的SSE指令：ADDPD/打包双精度加法，MULPD/打包双精度乘法

扩展讲解：这些内在函数允许程序员在C代码中直接使用SSE指令，从而在处理需要高性能计算的任务时充分利用CPU的向量处理能力。例如，使用__mm_load_pd可以将内存中的数据加载到SSE寄存器中，而__mm_add_pd和__mm_mul_pd则分别执行加法和乘法操作。通过这些本质函数，可以在不编写复杂汇编代码的情况下实现高效的并行计算。

Back to RISC-V: Vector Extensions (Draft)

RISC-V 向量扩展

• 提高RISC-V性能：添加SIMD指令（和硬件）——V扩展
  • 获取一条指令，完成多条指令的工作
  • OP表示一个向量指令，前缀v——向量寄存器
  • vadd vd, vs1, vs2（将两个向量寄存器中的向量相加）
  • 假设向量是512位宽的

RISC-V架构通过引入向量扩展（V扩展）来提升其处理并行计算的能力。向量扩展允许处理器一次处理多个数据元素，从而提高数据并行计算的效率。例如，vadd指令可以在一个指令周期内完成两个向量的加法运算，这对于大规模数据处理（如科学计算和图像处理）非常有用。与SSE指令类似，RISC-V的向量扩展也旨在通过并行化操作来加速数据处理任务。

And in Conclusion…

Flynn 分类法的并行架构

• SIMD（单指令多数据流）：单个指令在多个数据流上操作，适用于处理数据并行的任务，如图形处理、科学计算等。
• MIMD（多指令多数据流）：多个自主处理器同时执行不同的数据，适用于多核处理器和大规模计算机系统。
• SISD（单指令单数据流）：传统的单处理器系统，每个时刻只处理一个指令和一个数据。
• MISD（多指令单数据流）：较少应用的架构，多个指令在同一个数据流上操作。

SIMD和MIMD是现代并行计算中最常见的两种架构。SIMD用于需要大量相同操作的并行计算任务，例如图像处理和信号处理。MIMD则适用于需要处理不同任务的多处理器系统，例如服务器和超级计算机。SISD是传统计算机的工作方式，而MISD由于其应用场景有限，几乎没有被实际使用。

Intel AVX SIMD 指令

• 单条指令获取同时操作多个操作数
• 512/256/128/64位AVX寄存器
• 使用C本质函数

AVX（高级矢量扩展）是Intel处理器的一种指令集扩展，旨在提高并行计算性能。AVX指令可以在一个时钟周期内执行多个操作数的计算，通过使用更宽的寄存器（如512位寄存器），进一步提高数据处理的吞吐量。通过C本质函数，程序员可以在高层次语言中直接调用这些低级指令，简化了开发过程并提升了程序性能。

座右铭

• “过早优化是万恶之源（或至少是大多数罪恶的根源）”——Donald Knuth

这句名言提醒开发者在编写代码时不要过早进行优化，因为过早优化可能会使代码复杂化，增加维护难度。在进行性能优化时，应首先确保程序正确运行，然后再找出性能瓶颈，进行有针对性的优化。通过这种方式，可以在保持代码简洁和可维护性的同时，提升程序的执行效率。

Matrix Multiply Example

矩阵乘法示例

Application: Machine Learning

机器学习中的应用

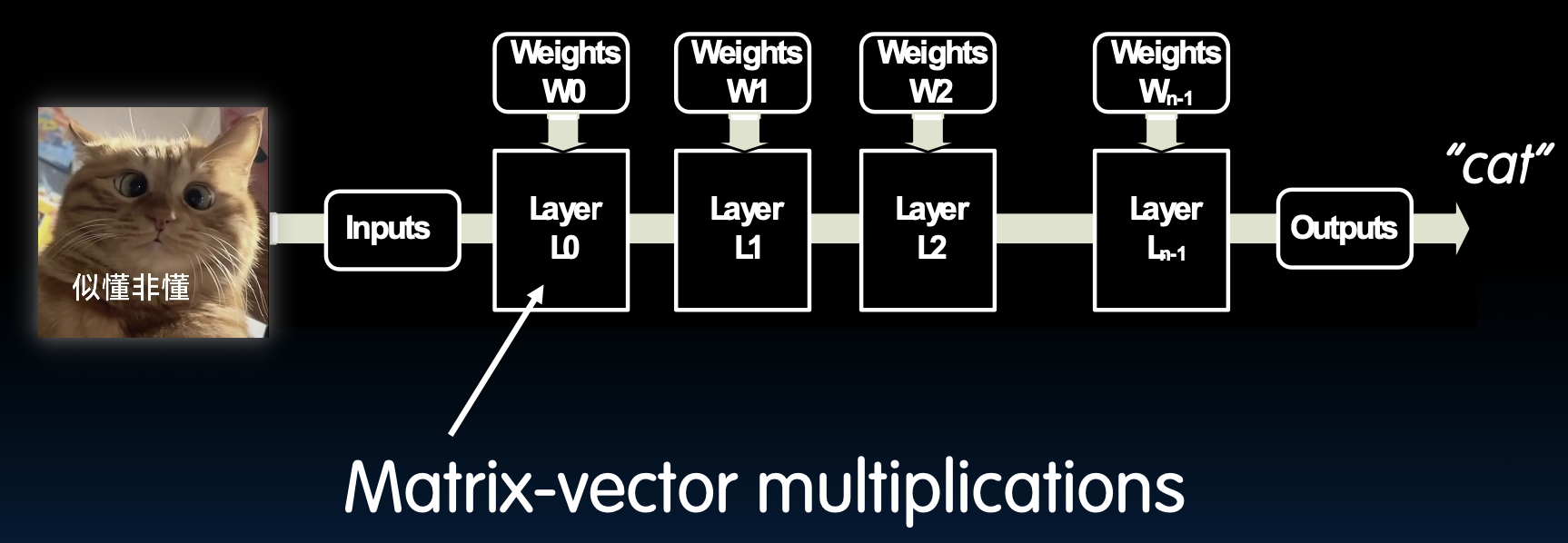
在机器学习应用中，推理是一个关键过程，它通过已经训练好的模型来对新的数据进行预测或分类。在图示的例子中，一个图像输入被处理并通过多个层的权重（Weights），最终输出一个分类结果，如“猫”。这个过程中涉及到大量的矩阵-向量乘法运算，这是神经网络中的基本操作。矩阵-向量乘法的高效实现对于提升机器学习模型的推理速度至关重要。

Reference Problem: Matrix Multiplication

矩阵乘法

• 基本操作：矩阵乘法是许多工程、数据处理和图像处理任务中的基本操作，如图像滤波、降噪和机器学习。
• 相关操作：许多与矩阵乘法密切相关的操作。
• dgemm：双精度浮点矩阵乘法，在FORTRAN中实现。

矩阵乘法不仅在理论上是线性代数的重要部分，在实际应用中也是计算密集型任务的核心。例如，在图像处理任务中，滤波操作可以表示为矩阵乘法；在机器学习中，前向传播和反向传播中的权重更新也大量依赖矩阵乘法。dgemm是BLAS（Basic Linear Algebra Subprograms）库中的一部分，用于高效地进行双精度浮点数的矩阵乘法运算。

Matrices

矩阵的表示

• 方阵：维度为NxN的方阵。
• 元素位置：使用(i, j)表示矩阵中的元素位置，i表示行，j表示列。

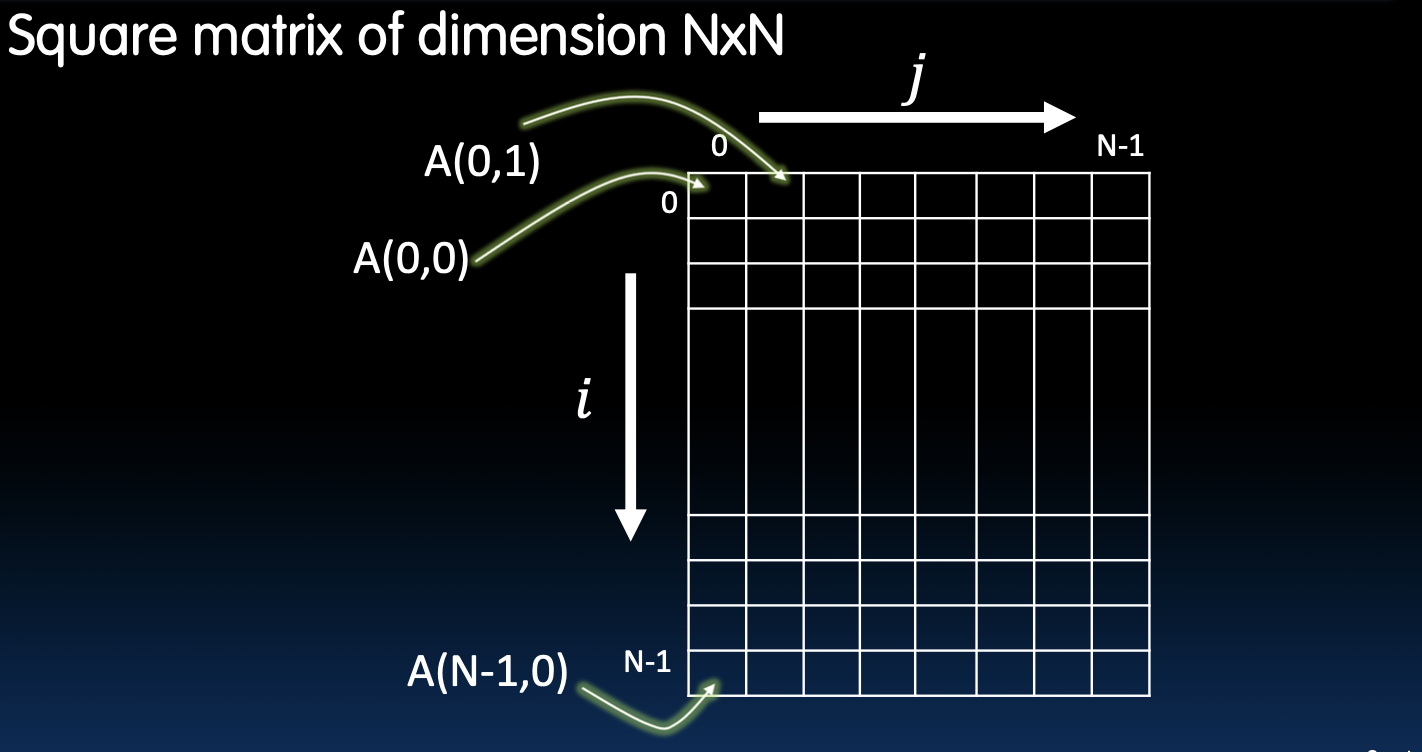
在方阵中，元素的定位非常重要，尤其是在进行矩阵运算时。对于一个NxN的方阵，A(i, j)表示第i行第j列的元素。在许多矩阵操作中，如矩阵乘法、转置等，明确每个元素的位置和其在计算中的作用是至关重要的。在图示中，A(0,0)表示矩阵的第一个元素，而A(N-1, N-1)则表示最后一个元素。理解这些基本概念是深入学习矩阵运算和并行计算优化的基础。

Matrix Multiplication

矩阵乘法

矩阵乘法是线性代数中的基本操作。对于两个矩阵A和B的乘积C，其计算公式为：

\[ C_{ij} = \sum_{k} A_{ik} \times B_{kj} \]

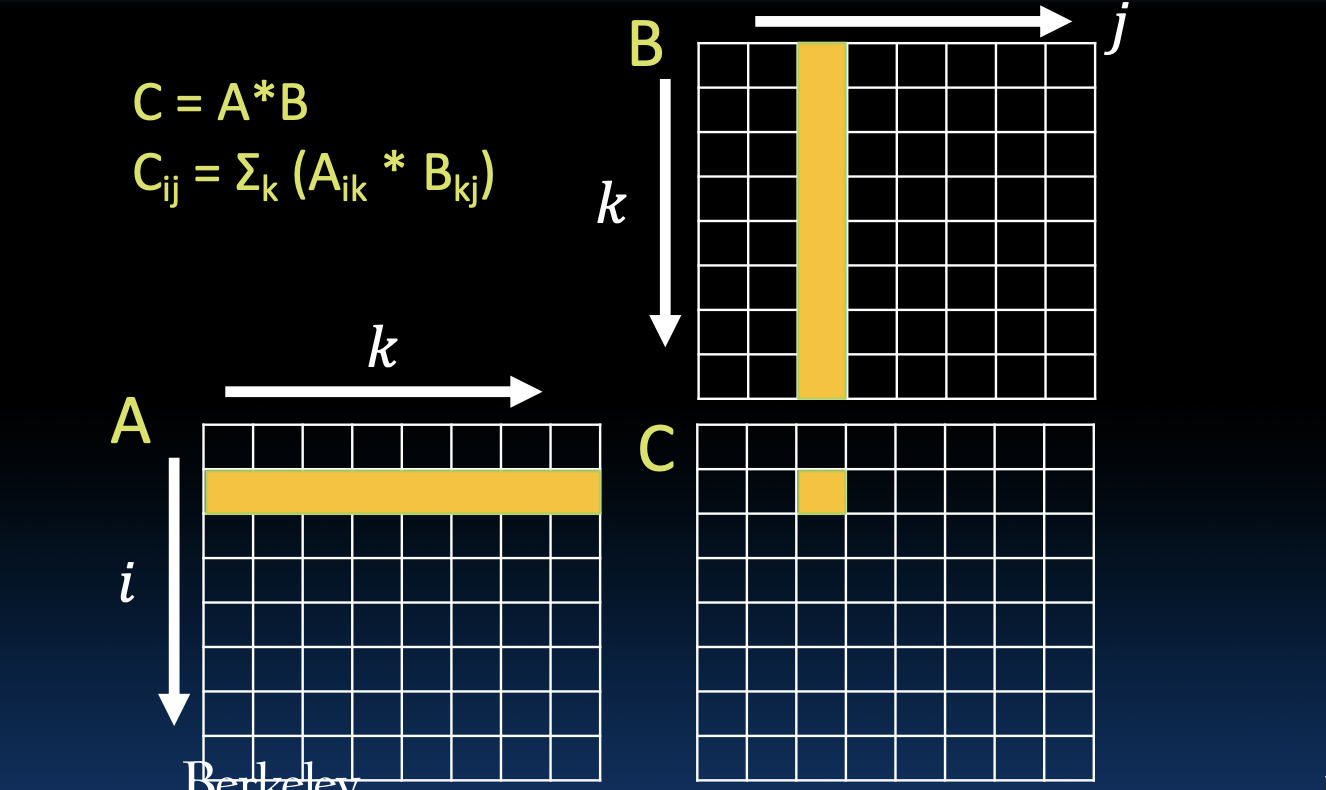
在图示中，矩阵A的第i行元素依次与矩阵B的第j列元素相乘并累加，得到矩阵C的第i行第j列元素。这个操作需要进行大量的乘法和加法运算，是计算密集型任务。

Example: 2 x 2 Matrix Multiply

2x2矩阵乘法示例

扩展讲解：考虑两个2x2矩阵的乘法示例：

Python中的矩阵乘法

在Python中，我们可以通过嵌套循环实现矩阵乘法。如下所示，函数dgemm实现了矩阵乘法，其中N表示矩阵的维度，a和b是输入矩阵，c是结果矩阵。

矩阵的数据结构表示

在这个例子中，矩阵被展平成一维数组进行存储。假设矩阵是N x N的，我们可以通过以下方式来表示：

• a[i + k * N]表示矩阵a中第i行第k列的元素。
• b[k + j * N]表示矩阵b中第k行第j列的元素。
• c[i + j * N]表示结果矩阵c中第i行第j列的元素。

代码示例

def dgemm(N, a, b, c):
    for i in range(N):
        for j in range(N):
            c[i + j * N] = 0  # 初始化结果矩阵的元素
            for k in range(N):
                c[i + j * N] += a[i + k * N] * b[k + j * N]  # 累加对应的乘积

在这个例子中，内层循环负责计算结果矩阵c的每个元素，通过累加对应的乘积。对于一个N维矩阵，dgemm函数需要进行大约2*N^3次浮点运算（FLOPs）。

性能结果表明，Python的实现每秒可以进行约5.4到5.5百万次浮点运算（MFLOPs）。

N	Python [MFLOPs]
32	5.4
160	5.5
480	5.4
960	5.3

这表明，随着矩阵维度的增加，Python的性能表现相对稳定。

C

矩阵乘法代码（C语言）

矩阵的数据结构表示

在C语言实现中，矩阵同样被展平成一维数组进行存储：

• a[i + k * N]表示矩阵a中第i行第k列的元素。
• b[k + j * N]表示矩阵b中第k行第j列的元素。
• c[i + j * N]表示结果矩阵c中第i行第j列的元素。

代码示例

void dgemm_scalar(int N, double *a, double *b, double *c) {
    for (int i = 0; i < N; i++) {  // 遍历结果矩阵的行
        for (int j = 0; j < N; j++) {  // 遍历结果矩阵的列
            double cij = 0;  // 初始化结果矩阵的元素
            for (int k = 0; k < N; k++) {  // 遍历并累加对应的乘积
                cij += a[i + k * N] * b[k + j * N];
            }
            c[i + j * N] = cij;  // 将计算结果存储到结果矩阵
        }
    }
}

这个C语言实现的矩阵乘法函数dgemm_scalar，使用了三重循环来遍历矩阵的每个元素进行乘法和加法运算。i和j分别遍历结果矩阵的行和列，k用于计算对应的元素乘积并累加到结果矩阵的相应位置。这种实现方式可以直接利用C语言的高效内存操作和计算能力，因此在执行速度上比Python实现更快。

Timing Program Execution

计时程序执行时间（C语言）

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

int main(void) {
    clock_t start = clock();
    
    // 需要计时的任务
    dgemm(N, ...);
    
    clock_t end = clock();
    double delta_time = (double)(end - start) / CLOCKS_PER_SEC;
    printf("Execution time: %f seconds\n", delta_time);
    return 0;
}

在这个C语言程序中，使用clock()函数来计时。clock()函数返回从程序启动到调用时所使用的处理器时间。通过记录任务开始和结束时的时间，可以计算出任务的执行时间，并将其转换为秒数进行输出。这种方法适用于需要精确测量代码性能的情况。

C vs. Python

C与Python性能比较

N	Python [GFLOPS]	C [GFLOPS]
32	0.0054	1.30
160	0.0055	1.30
480	0.0054	1.32
960	0.0053	0.91

从表格中可以看出，C语言在矩阵乘法的性能上比Python快了约240倍。GFLOPS（每秒十亿次浮点运算）是衡量计算性能的重要指标。C语言的高性能主要得益于其底层操作的高效性和编译优化，而Python由于是解释型语言，在执行速度上相对较慢。因此，对于计算密集型任务，如矩阵乘法，使用C语言实现可以显著提高性能。

通过将相同的矩阵乘法算法用不同语言实现，可以明显看到C语言在执行效率上的优势。通过优化代码和选择合适的编程语言，可以在实际应用中获得更高的计算性能和更好的用户体验。

Example: 2 x 2 矩阵乘法

矩阵乘法公式

SIMD 指令的实现

在使用 SIMD（单指令多数据）指令进行矩阵乘法时，可以通过一次加载多个元素并同时进行计算来提高效率。例如，在 Intel 的 SSE 指令集中，可以使用 _mm_load_pd 指令一次加载两个 double 型数值到寄存器，并使用 _mm_mul_pd 进行并行乘法计算，从而大大加快运算速度。

这种方法利用了数据级并行性，可以显著减少计算时间，特别是在处理大型矩阵时，效果更加明显。通过使用适当的 SIMD 指令，计算可以更高效地执行，同时减少处理器的空闲时间，提高整体系统性能。

Example: 2 x 2 矩阵乘法

初始化结果矩阵 (C)

首先，我们需要初始化结果矩阵 (C) 为零矩阵：

矩阵乘法步骤

I = 1, 中间结果

对于 (i=1)，我们计算第一列的中间结果。

1. 计算 (C_{1,1}) 和 (C_{2,1})：

   \[ C_{1,1} = 0 + A_{1,1} \times B_{1,1} = 0 + 1 \times 1 = 1 \] \[ C_{2,1} = 0 + A_{2,1} \times B_{1,1} = 0 + 0 \times 1 = 0 \]

2. 计算 (C_{1,2}) 和 (C_{2,2})：

   \[ C_{1,2} = 0 + A_{1,1} \times B_{1,2} = 0 + 1 \times 3 = 3 \] \[ C_{2,2} = 0 + A_{2,1} \times B_{1,2} = 0 + 0 \times 3 = 0 \]

此时的中间结果为：

\[ C = \begin{pmatrix} 1 & 3 \\ 0 & 0 \end{pmatrix} \]

使用 SIMD 指令实现

在这里，我们可以使用 SIMD 指令加速计算。例如，使用 _mm_load_pd 将矩阵 (A) 和 (B) 的数据加载到 SSE 寄存器中，然后使用 _mm_mul_pd 和 _mm_add_pd 并行地进行乘法和加法操作。

__m128d a1 = _mm_load_pd(&A[0]);
__m128d b1 = _mm_load_pd(&B[0]);
__m128d c1 = _mm_mul_pd(a1, b1);
__m128d result = _mm_add_pd(c1, c1);

I = 2, 中间结果

对于 (i=2)，我们计算第二列的中间结果。

1. 计算 (C_{1,1}) 和 (C_{2,1})：

   \[ C_{1,1} = C_{1,1} + A_{1,2} \times B_{2,1} = 1 + 0 \times 2 = 1 \] \[ C_{2,1} = C_{2,1} + A_{2,2} \times B_{2,1} = 0 + 1 \times 2 = 2 \]

2. 计算 (C_{1,2}) 和 (C_{2,2})：

   \[ C_{1,2} = C_{1,2} + A_{1,2} \times B_{2,2} = 3 + 0 \times 4 = 3 \] \[ C_{2,2} = C_{2,2} + A_{2,2} \times B_{2,2} = 0 + 1 \times 4 = 4 \]

最终结果

通过上述计算，我们最终得到结果矩阵 (C)：

\[ C = \begin{pmatrix} 1 & 3 \\ 2 & 4 \end{pmatrix} \]

这种计算过程展示了如何通过逐步计算矩阵元素来实现矩阵乘法。使用 SIMD 指令可以显著加快计算速度，因为它们可以并行处理多个数据元素，从而减少总体计算时间。

Example: 2 x 2 矩阵乘法

代码解释

以下是一个使用SSE指令进行2x2矩阵乘法的示例代码。这个代码使用了SIMD（单指令多数据）技术来加速矩阵乘法的计算。

#include <stdio.h>
// 包含SSE编译器内置函数的头文件
#include <emmintrin.h>

// 注意：向量寄存器将在注释中表示为 v1 = [ a | b ]
// 其中 v1 是类型为 __m128d 的变量，a 和 b 是 double 类型

int main(void) {
    // 将A, B, C矩阵对齐到16字节边界
    double A[4] __attribute__ ((aligned (16)));
    double B[4] __attribute__ ((aligned (16)));
    double C[4] __attribute__ ((aligned (16)));
    int lda = 2;
    int i = 0;

    // 声明几个128位向量变量
    __m128d c1, c2, a, b1, b2;

    // 初始化A, B, C矩阵，例如
    /*
    * A = (注意列优先顺序！)
    * 1 0
    * 0 1
    */
    A[0] = 1.0; A[1] = 0.0; 
    A[2] = 0.0; A[3] = 1.0;

    /*
    * B = (注意列优先顺序！)
    * 1 2
    * 3 4
    */
    B[0] = 1.0; B[1] = 2.0; 
    B[2] = 3.0; B[3] = 4.0;

    /*
    * C = (注意列优先顺序！)
    * 0 0
    * 0 0
    */
    C[0] = 0.0; C[1] = 0.0; 
    C[2] = 0.0; C[3] = 0.0;

    // 使用对齐加载设置
    // c1 = [c_11 | c_21]
    c1 = _mm_load_pd(C+0*lda);
    // c2 = [c_12 | c_22]
    c2 = _mm_load_pd(C+1*lda);

    for (i = 0; i < 2; i++) {
        // a = [a_i1 | a_i2]
        a = _mm_load_pd(A+i*lda);

        // b1 = [b_1i | b_1(i+1)]
        b1 = _mm_load1_pd(B+i+0*lda);
        // b2 = [b_2i | b_2(i+1)]
        b2 = _mm_load1_pd(B+i+1*lda);

        /*
        * c1 = [c_11 | c_21] += [a_i1*b_1i | a_i2*b_1i]
        * c2 = [c_12 | c_22] += [a_i1*b_2i | a_i2*b_2i]
        */
        c1 = _mm_add_pd(c1, _mm_mul_pd(a, b1));
        c2 = _mm_add_pd(c2, _mm_mul_pd(a, b2));
    }

    // 将c1, c2存回C矩阵以完成计算
    _mm_store_pd(C+0*lda, c1);
    _mm_store_pd(C+1*lda, c2);

    // 打印C矩阵
    printf("%g, %g\n%g, %g\n", C[0], C[1], C[2], C[3]);
    return 0;
}

代码详解

1. 头文件引入

   #include <stdio.h>
   #include <emmintrin.h>
   

   • 引入标准输入输出头文件<stdio.h>。
   • 引入SSE编译器内置函数头文件<emmintrin.h>。
2. 主函数

   int main(void) {
       // 将A, B, C矩阵对齐到16字节边界
       double A[4] __attribute__ ((aligned (16)));
       double B[4] __attribute__ ((aligned (16)));
       double C[4] __attribute__ ((aligned (16)));
       int lda = 2;
       int i = 0;
      
       // 声明几个128位向量变量
       __m128d c1, c2, a, b1, b2;
   

   • 声明并分配对齐的矩阵A、B、C。
   • 定义lda为矩阵的维度（2x2矩阵）。
   • 声明用于存储中间结果的128位向量变量。
3. 初始化矩阵

       A[0] = 1.0; A[1] = 0.0; A[2] = 0.0; A[3] = 1.0;
       B[0] = 1.0; B[1] = 2.0; B[2] = 3.0; B[3] = 4.0;
       C[0] = 0.0; C[1] = 0.0; C[2] = 0.0; C[3] = 0.0;
   

   • 初始化矩阵A、B和C。
4. 加载初始值到向量寄存器

       c1 = _mm_load_pd(C+0*lda);
       c2 = _mm_load_pd(C+1*lda);
   

   • 使用SSE指令将矩阵C的初始值加载到向量寄存器c1和c2。
5. 矩阵乘法计算

       for (i = 0; i < 2; i++) {
           a = _mm_load_pd(A+i*lda);
           b1 = _mm_load1_pd(B+i+0*lda);
           b2 = _mm_load1_pd(B+i+1*lda);
      
           c1 = _mm_add_pd(c1, _mm_mul_pd(a, b1));
           c2 = _mm_add_pd(c2, _mm_mul_pd(a, b2));
       }
   

   • 使用嵌套循环遍历矩阵A的每一行，加载A和B的对应元素。
   • 通过SSE指令进行矩阵乘法和累加操作。
6. 存储计算结果并输出

       _mm_store_pd(C+0*lda, c1);
       _mm_store_pd(C+1*lda, c2);
      
       printf("%g, %g\n%g, %g\n", C[0], C[1], C[2], C[3]);
       return 0;
   }
   

   • 将向量寄存器中的结果存储回矩阵C。
   • 打印矩阵C的计算结果。

这个示例展示了如何利用SSE指令进行2x2矩阵乘法，通过使用向量化技术，可以显著提高计算效率。

C 与 Python 的性能对比

性能对比表

N	Python [GFLOPS]	C [GFLOPS]	AVX [GFLOPS]
32	0.0054	1.30	4.56
160	0.0055	1.30	5.47
480	0.0054	1.32	5.27
960	0.0053	0.91	3.64

理论性能

理论上的 Intel i7-5557U 性能约为 25 GFLOPS：

\[ 3.1 \text{GHz} \times 2 \text{指令/周期} \times 4 \text{乘法/指令} = 24.8 \text{GFLOPS} \]

在实际应用中，使用 C 语言和 SIMD 指令（如 AVX 指令集）可以显著提升计算性能，相比 Python 实现的速度提升可达 240 倍甚至更多。这表明，在计算密集型任务中，选择合适的编程语言和优化技术（如向量化）是至关重要的。