Lecture 17: Combinational Logic Blocks

数据多路复用器（Data Multiplexor, 简称 MUX）

多路复用器是一种组合逻辑电路，它能够从多个输入信号中选择一个作为输出。图中展示的是一个2-to-1的n-bit宽度的多路复用器（MUX）。

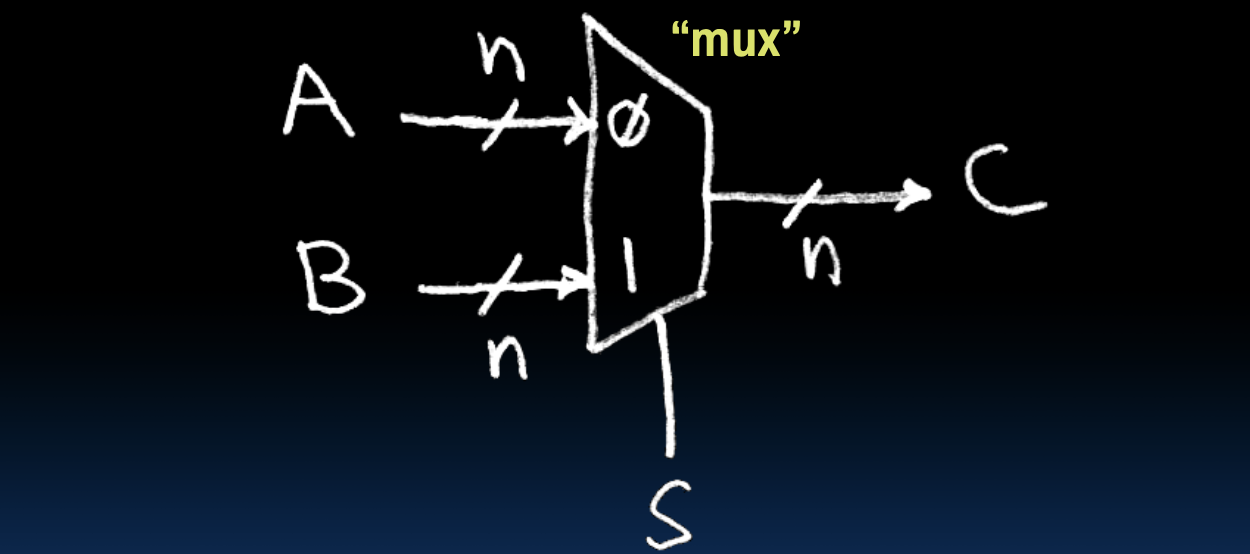
image-20240803123246599

  • 输入端：A和B，每个有n个位。
  • 选择信号：S，用于选择输出是来自A还是B。
  • 输出端：C，与选择信号S对应的输入端相连，输出为n个位。

1-bit宽度MUX实例

N个1-bit宽度的MUX实例

1-bit宽度的MUX实例可以通过布尔代数表示，如下所示：

  • 布尔表达式：c = s̅ab̅ + s̅ab + sa̅b + sab
  • 通过化简得到：c = s̅a + sb

对于一个1-bit宽度的MUX，真值表如下，通过选择信号s的值，决定输出c是选择输入a还是输入b。

image-20240803123436167

如何构建一个1-bit宽度的MUX？

逻辑电路实现

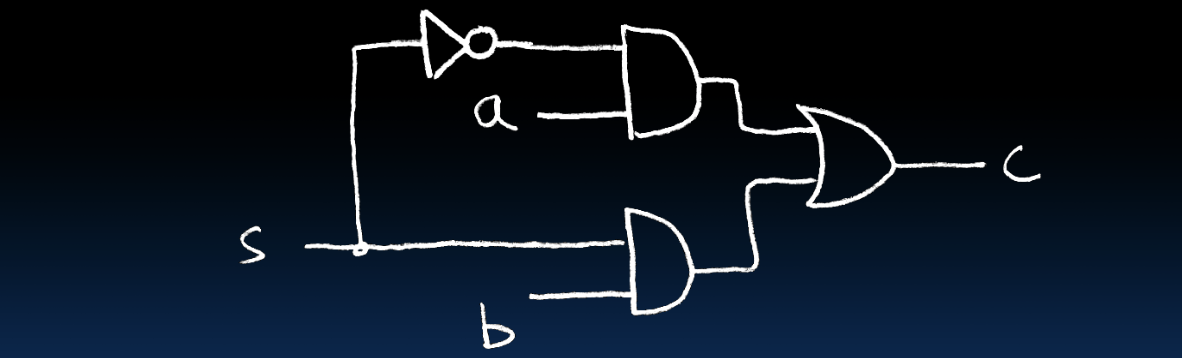
1-bit宽度的MUX可以用简单的逻辑门（与门、或门、非门）实现，其布尔表达式为：c = s̅a + sb。

  • 选择信号s的非门输出s̅，用于选择a。
  • 选择信号s直接用于选择b。
  • 两个与门的输出通过一个或门合并，得到最终的输出c。

这个逻辑电路的具体实现如图所示：当s为0时，选择a作为输出；当s为1时，选择b作为输出。

image-20240803123753835

##

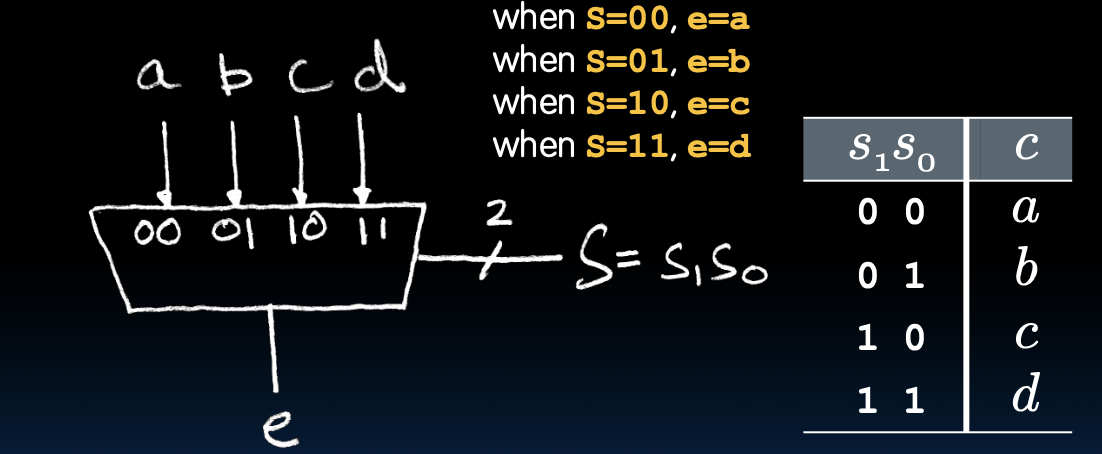
4-to-1多路复用器的实现

4-to-1多路复用器可以用来选择4个输入中的一个输出，其选择信号为2位（s1和s0）。

s1 s0 c
0 0 a
0 1 b
1 0 c
1 1 d

布尔表达式

根据选择信号的组合，布尔表达式可以写成： image-20240803123908694

这个表达式表示当选择信号s1s0为00时，输出为a；当选择信号s1s0为01时，输出为b；依此类推。

image-20240803123929902

分层实现（Hierarchical Implementation）

4-to-1多路复用器可以通过分层的方式实现，即用2个2-to-1多路复用器的输出作为另一个2-to-1多路复用器的输入。

  • 第一层：两个2-to-1多路复用器分别处理a、b和c、d。
  • 第二层：一个2-to-1多路复用器处理第一层的输出。

这种分层设计不仅可以简化电路设计，还可以提高电路的模块化和可维护性。

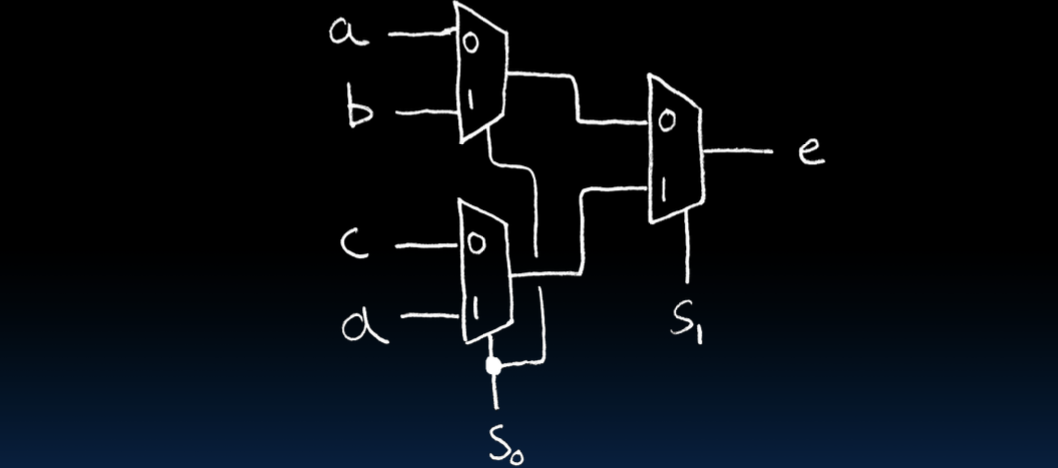
image-20240803124158399

图示展示了一个4-to-1多路复用器的分层实现，其中两个选择信号s0和s1分别控制不同层次的MUX，以实现最终的选择输出。

通过这种方式，复杂的多路复用器可以逐步拆解为更简单的2-to-1多路复用器，从而简化设计过程，并增强电路的灵活性和可扩展性。

算术逻辑单元（ALU）

大多数处理器包含一个特殊的逻辑模块，称为“算术和逻辑单元”（ALU）。

  • 功能：ALU执行基本的算术和逻辑操作，如加法（ADD）、减法（SUB）、按位与（AND）和按位或（OR）。

简单的ALU实现

在图中，我们展示了一个简单的ALU，它能够执行以下操作：

  • 当选择信号S为00时，执行加法操作：R = A + B。
  • 当选择信号S为01时，执行减法操作：R = A - B。
  • 当选择信号S为10时，执行按位与操作：R = A & B。
  • 当选择信号S为11时，执行按位或操作：R = A B。

这些操作的选择由选择信号S控制，通过改变S的值，可以选择不同的操作。

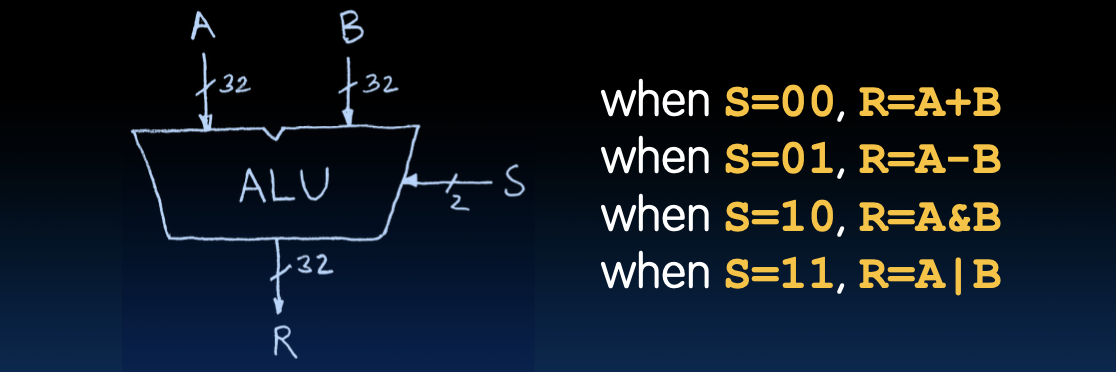
image-20240803124254124

结构图

图中展示了一个简单的ALU结构，它包括以下组件：

  • 加法/减法模块：根据选择信号So决定执行加法或减法操作。
  • 按位与模块：执行按位与操作。
  • 按位或模块：执行按位或操作。
  • 多路复用器：根据选择信号S0和S1选择最终的输出结果。

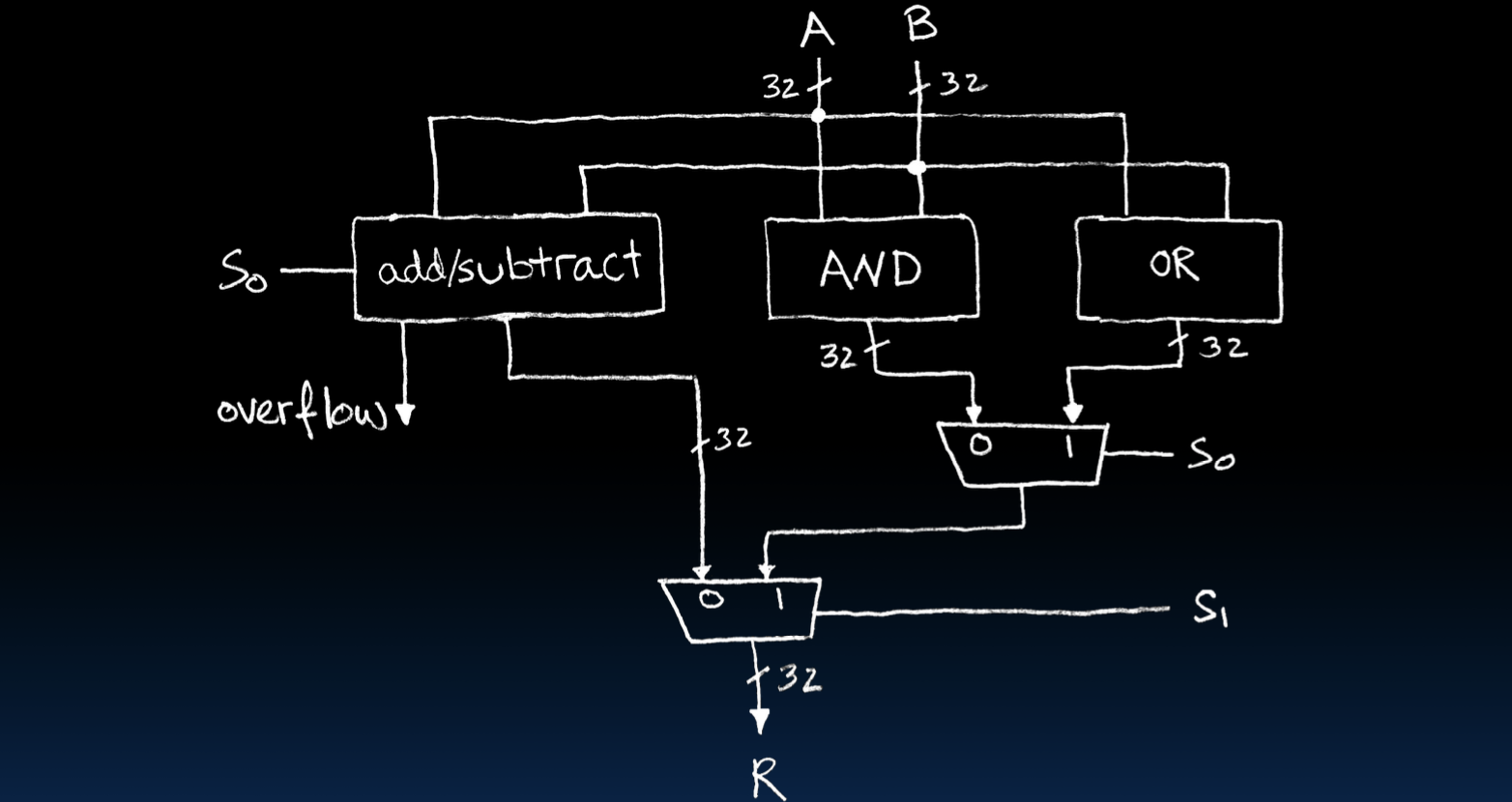
image-20240803124411692

工作原理

  • 加法/减法模块：根据选择信号So的值决定是执行加法还是减法操作，并输出结果。
  • 按位与模块：执行A和B的按位与操作，并输出结果。
  • 按位或模块：执行A和B的按位或操作，并输出结果。
  • 多路复用器：根据选择信号S0和S1选择加法/减法模块、按位与模块或按位或模块的输出作为最终结果R。

通过这种结构设计，ALU能够灵活地执行多种基本算术和逻辑操作，为处理器提供了强大的计算能力。

Adder / Subtracter

加法器/减法器设计 - 如何实现？

设计步骤

  1. 真值表：首先确定真值表，然后确定标准形式，再进行最小化和实现。
  2. 分解问题：将问题分解成可以级联或分层的小块，以便更易于处理和实现。

一位加法器 - 最低有效位（LSB）

在设计加法器时，首先需要考虑最基本的一位加法。一个一位加法器有两个输入位$a_0$和$b_0$，以及一个进位输入$c_0$。它的输出包括一个和位$s_0$和一个进位输出$c_1$。

真值表展示了所有可能的输入组合及其对应的输出：

  • 当$a_0 = 0$，$b_0 = 0$，$c_0 = 0$时，$s_0 = 0$，$c_1 = 0$。
  • 当$a_0 = 0$，$b_0 = 1$，$c_0 = 0$时，$s_0 = 1$，$c_1 = 0$。
  • 当$a_0 = 1$，$b_0 = 0$，$c_0 = 0$时，$s_0 = 1$，$c_1 = 0$。
  • 当$a_0 = 1$，$b_0 = 1$，$c_0 = 0$时，$s_0 = 0$，$c_1 = 1$。

通过分析真值表，可以得出以下公式：

  • 和位$s_0 = a_0 \oplus b_0$
  • 进位输出$c_1 = a_0 \land b_0$

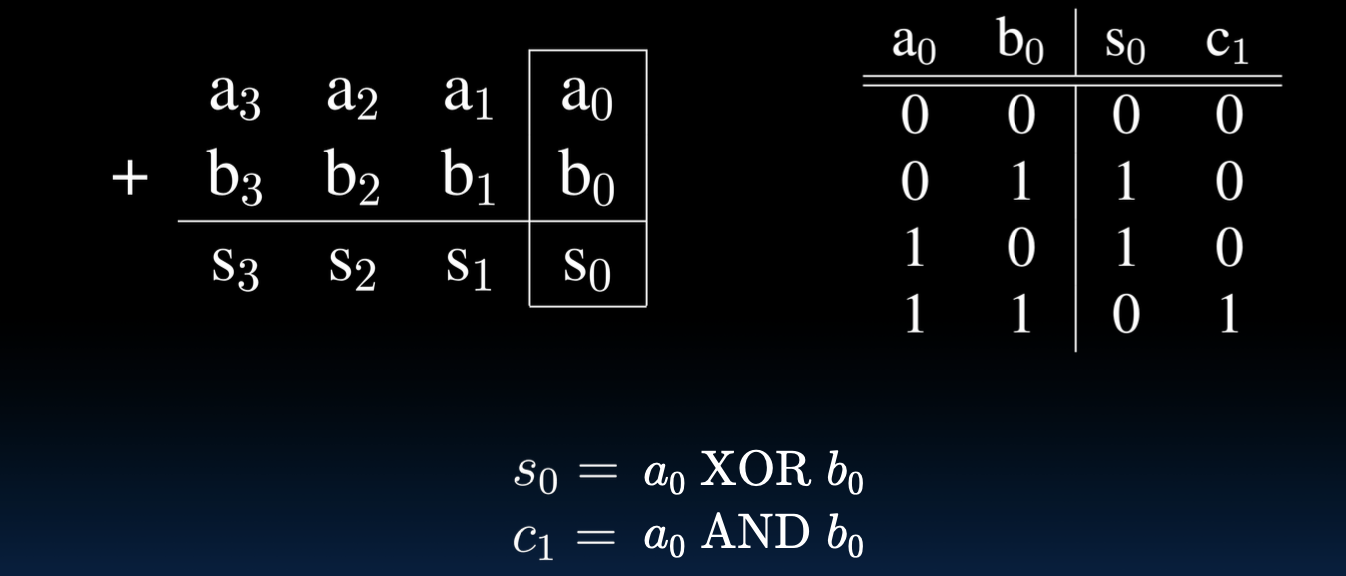
image-20240803130607337

加法器/减法器 - 一位加法器

为了处理多位加法，需要设计一个全加器（Full Adder），它在考虑进位输入的同时执行加法操作。对于每个位$i$，全加器的输入包括两个加数位$a_i$和$b_i$，以及一个进位输入$c_i$。它的输出包括一个和位$s_i$和一个进位输出$c_{i+1}$。

全加器的真值表展示了所有可能的输入组合及其对应的输出：

  • 当$a_i = 0$，$b_i = 0$，$c_i = 0$时，$s_i = 0$，$c_{i+1} = 0$。
  • 当$a_i = 0$，$b_i = 1$，$c_i = 0$时，$s_i = 1$，$c_{i+1} = 0$。
  • 当$a_i = 1$，$b_i = 0$，$c_i = 0$时，$s_i = 1$，$c_{i+1} = 0$。
  • 当$a_i = 1$，$b_i = 1$，$c_i = 0$时，$s_i = 0$，$c_{i+1} = 1$。
  • 其他组合同理。

image-20240803131156735

通过分析真值表，可以得出以下公式：

  • 和位$s_i = a_i \oplus b_i \oplus c_i$
  • 进位输出$c_{i+1} = (a_i \land b_i) \lor (a_i \land c_i) \lor (b_i \land c_i)$

这些公式说明了如何通过逻辑运算来实现全加器的功能。

更多细节见 MIT 6.004 Full Adder 或学习MIT 6.004 L05-L08

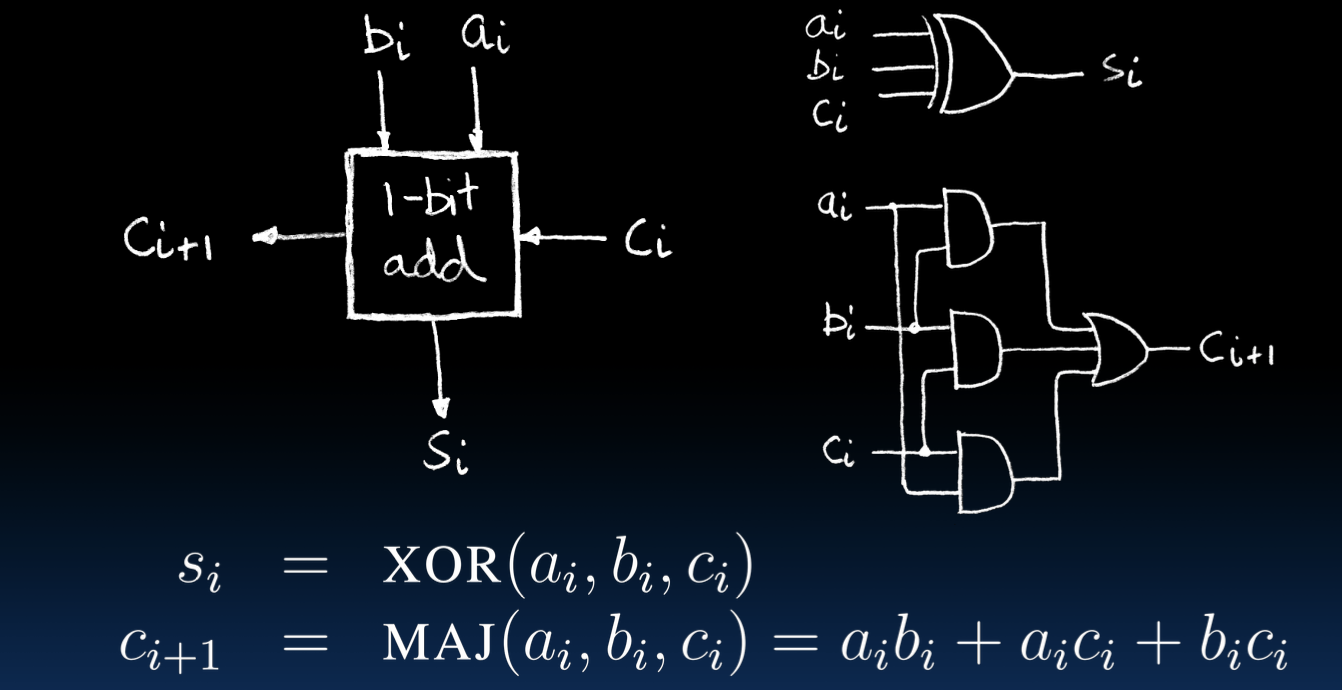
image-20240803140227894

图示展示了如何使用XOR和AND门来构建一个一位加法器。

公式解释：

  • 和位$s_i = \text{XOR}(a_i, b_i, c_i)$
  • 进位输出$c_{i+1} = \text{MAJ}(a_i, b_i, c_i)$，即$a_i b_i + a_i c_i + b_i c_i$

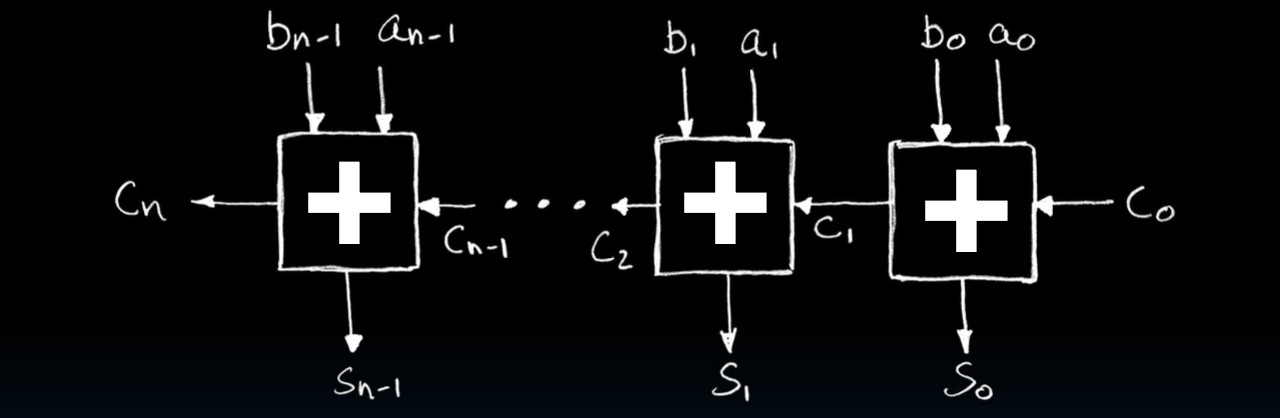
N位加法器

通过将多个一位加法器级联，可以实现一个多位加法器。例如，N位加法器可以由N个一位加法器级联而成。每个加法器的进位输出作为下一个加法器的进位输入，最终的进位输出$C_n$表示溢出。

image-20240803140318190

两个2位数的加法

无符号数加法

图示展示了两个2位数相加的过程及其真值表。

image-20240803142254844

图示展示了两个 2 位二进制数的求和过程，并讨论了求和过程中可能出现的溢出情况。这里我们先从基本概念开始。

  • a 和 b: 两个加数，每个加数有 2 位，分别表示为 (a_1, a_0) 和 (b_1, b_0)。
  • s: 求和结果，每位分别表示为 (s_1, s_0)。
  • c: 进位，每位分别表示为 (c_1) 和 (c_2)（其中 (c_0) 为输入进位，通常为 0）。

真值表和求和示例

在表格中列出了所有可能的 2 位二进制数的和：

  • 00, 01, 10, 11 分别表示 0, 1, 2, 3。
  • 表格中的每一行展示了两个 2 位二进制数的和，例如：01 + 01 = 10。

进位和溢出判断

  • 无符号数求和: 当两个数的和需要超过 2 位时，产生进位。例如，10 + 10 = 100，需要 3 位来表示。
  • 有符号数求和（补码表示）: 当最高位的进位 (c_1) 和次高位的进位 (c_2) 不一致时，会产生溢出。

溢出例子

在图示中的有符号数：

  • (11 + 11 = 110)：(c_2 = 1)，但没有溢出，因为 (c_1 = 1)。
  • (10 + 10 = 100)：(c_2 = 1)，且 (c_1 = 0)，溢出。
  • (01 + 01 = 10)：没有溢出，因为 (c_2 = 0) 且 (c_1 = 1)。

溢出（Overflow）的定义

  1. 无符号数溢出：当结果需要更多位数来表示时，发生溢出。
  2. 有符号数溢出：当最高有效位（MSB）的进位 \(c_1\) 和次高有效位（MSB-1）的进位 \(c_2\) 不一致时，发生溢出。判断溢出可以通过异或操作来完成，即 \( \text{overflow} = c_1 \oplus c_0 \)。

分析 \(11 + 01\) 的溢出情况

我们来逐步分析 \(11 + 01\) 的二进制加法过程：

  1. 二进制表示和加法

    • \(a = 11\) 对应的十进制值为 -1（补码表示）。
    • \(b = 01\) 对应的十进制值为 1。

    现在我们进行逐位加法：

    1 1
  + 0 1
-----
    0 0  (sum)  with carry = 1
  1. 进位分析
    • 第0位（最低位）的加法：\(1 + 1 = 10\)，得到0，并向第1位进1。
    • 第1位（最高位）的加法：\(1 + 0 + 进位1 = 10\)，得到0，并向最高位进1。
  2. 结果
    • 最终结果为 00（和为 0），最高位有进位。

溢出判断

对于 \(11 + 01\) 这个加法操作，我们需要看它在不同情况下的溢出情况。

无符号数

  • 无符号数 \(11\) 表示 3，\(01\) 表示 1。求和 \(3 + 1 = 4\)，需要更多位来表示，所以无符号数是溢出的。

有符号数（补码）

  • 对于有符号数，\(11\) 表示 -1，\(01\) 表示 1。求和 \(-1 + 1 = 0\)，在补码表示下，结果为 00，表示没有溢出。

具体分析进位情况

  1. 无溢出情况：
    • 如果两个正数相加，结果仍为正数。
    • 如果两个负数相加，结果仍为负数。
    • 在这两种情况下，从次高位（倒数第二位）到最高位的进位和从最高位到最高位之外的进位是一致的（即 \(c_{n-1} = c_n\)）。
  2. 溢出情况：
    • 如果两个正数相加，结果为负数。
    • 如果两个负数相加，结果为正数。
    • 在这两种情况下，从次高位（倒数第二位）到最高位的进位和从最高位到最高位之外的进位是不一致的（即 \(c_{n-1} \neq c_n\)）。

有符号数加法（补码）

在进行有符号数（补码）加法时，需要注意溢出情况。溢出的判断依据是最高位的进位$C_n$和次高位的进位$C_{n-1}$是否一致：

  • 若$C_n \neq C_{n-1}$，则发生溢出。

公式：

  • 溢出判断$overflow = C_n \oplus C_{n-1}$

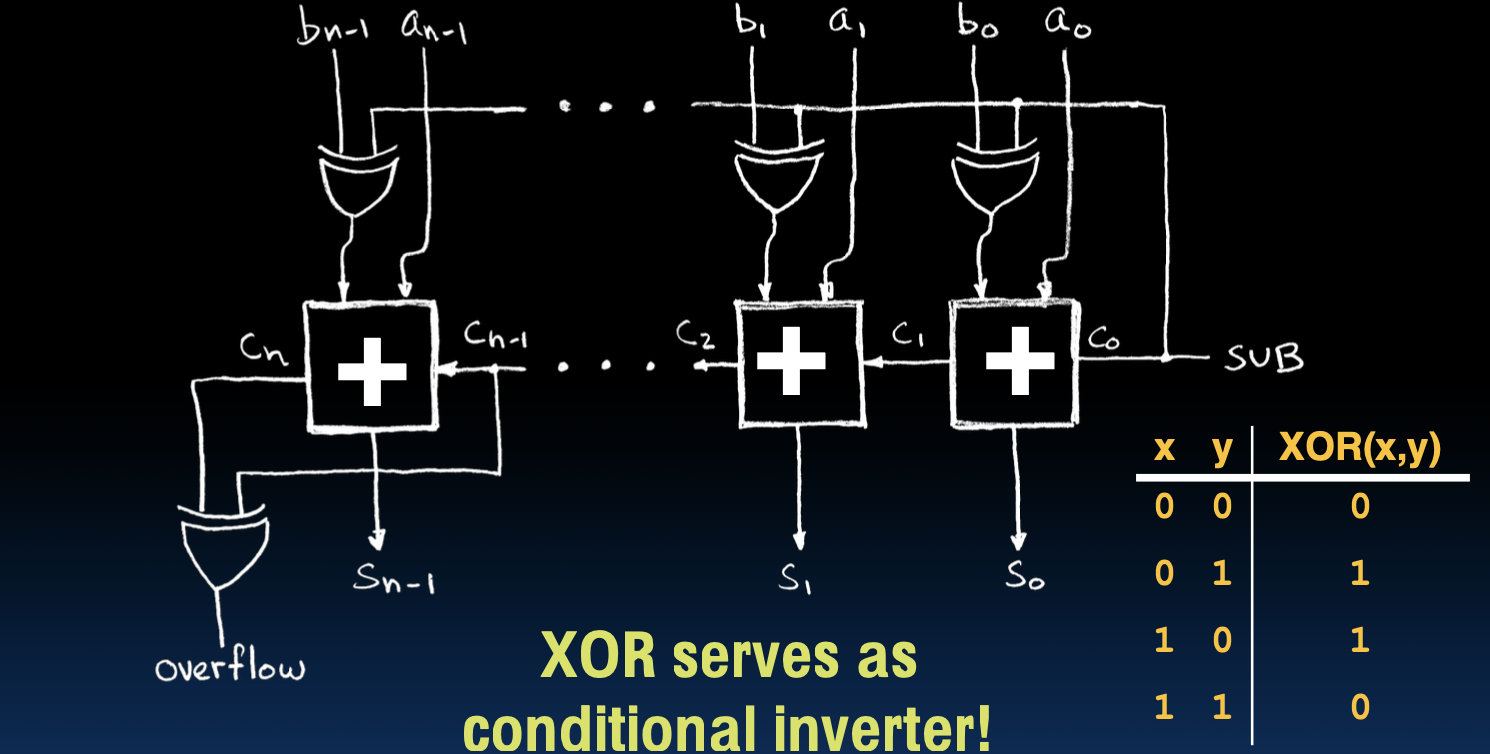
Subtractor Design

巧妙的减法器：A-B = A + (-B)

极其巧妙的减法器设计

减法器可以通过加法器来实现，通过将被减数取反然后加上被减数的补码来完成减法运算。图示展示了这一过程：

  • XOR门作为条件反相器，可以将被减数进行条件取反。
  • 进位链通过多个加法器级联，实现多位数的减法。

这个设计的关键在于XOR门的使用，确保输入信号根据需要进行取反，从而实现A - B的操作。

image-20240803150703917

问题

  1. 具有4位信号的多路复用器的真值表有多少行？
  2. 我们可以级联N个1位移位器来制作1个N位移位器？

答案

真值表的行数是控制信号和数据输入信号的组合数量。对于一个4位控制信号的多路复用器，其真值表的行数为：

\[ 2^{4} \times 2^{16} \]

  • 控制信号：4位控制信号有 (2^4 = 16) 种组合。
  • 数据输入信号：16个数据输入信号，每个信号可以是0或1，有 (2^{16}) 种组合。

将这两者结合起来，总的组合数为：

\[ 2^4 \times 2^{16} = 2^{20} \]

示例真值表

下面是一个简化的真值表，展示了控制信号和数据输入信号的组合如何决定输出：

S3 S2 S1 S0 I0 I1 I2 I3 I4 I5 I6 I7 I8 I9 I10 I11 I12 I13 I14 I15 输出
0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 I0
0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 I1
0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 I2
0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 I3
1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 I15

每一行代表一个可能的输入组合，其中4位控制信号选择一个特定的数据输入信号作为输出。真值表中所有可能的组合数为 (2^{20})，即 (2^4 \times 2^{16})。

结论

  • 使用多路复用器来选择输入：S个控制信号选择2^S个输入。每个输入可以是n位宽，与S无关。
  • 可以分层次实现多路复用器。
  • ALU可以使用多路复用器实现，与基本模块元素结合。
  • 使用N个1位加法器和输入上的XOR门可以实现N位加减法器，XOR门作为条件反相器。

© 2024 LzzsSite
该笔记由 LzzsG 基于 CS 61C / Garcia, Yan 的作品创作，采用的是 CC BY-NC-SA 许可。

Edit this page on GitHub.