Lecture 3. Control

Textbook Ch. 1.3 Ch. 1.4 Ch. 1.5

公告

实验（Lab）截止日期

• Lab 0 和 Lab 1 马上就要截止了。
  • Lab 0 不计入成绩，但它非常重要，帮助你完成计算机环境的设置。
  • Lab 1 是计入成绩的，截止时间为周一晚上 11:59（太平洋时间）。
  • 如果你身处不同的时区（尤其是欧洲时区），并且觉得这个截止时间不方便，请发送邮件至 [email protected]，申请延长至周二。

实验结构与指导

• 实验相较于作业更为简单，预计完成时间为1.5小时左右。
• Lab 指导时间安排：
  • 下午2:00：同时进行两个指导会，一个是面向所有学生，另一个是为编程经验较少的学生准备的。
  • 下午6:00、下午7:00（为编程经验较少的学生提供）、下午9:00 还有额外的指导会。
  • 对于编程经验较少的同学，建议参加为其量身定制的指导会，那里提出的问题可能会更符合入门学生的需求。
  • 每场实验指导由不同的助教负责，但内容是相同的。
  • 形式：通过 Zoom 以网络研讨会的形式进行，问题通过 Q&A 工具提交，一些问题将通过文字回答，另一些会通过口头回答。
  • 我们计划将所有会议录制并发布到 bCourses，但建议你现场参加，以便实时提问并获得帮助。

实验提交

• 在参加指导后，完成 Lab 1，并通过与提交 Lab 0 相同的方式提交。
• 实验可以自由合作 —— 你可以和其他同学共享代码，一起解决问题。但请记住，实验是为了学习，确保你真正理解了所学内容。
• 实验作业不会严格检查代码抄袭，但如果不通过实验掌握解决问题的技能，后续的作业和考试将会遇到很大困难。

作业 1

• 作业 1 已经发布，截止时间为周四。
  • 与实验不同，作业中禁止共享或抄袭代码。
  • 你可以讨论解决问题的策略，但不能分享代码。
  • 你可以通过 Piazza 或访问 oh.cs61a.org 办公室时间获得帮助。
• 你可以在办公室时间系统中组队，并为团队请求助教的帮助。
• 预约将在前一天晚上10:00左右开放，预约不限于特定任务，因此你可以针对任何实验或作业寻求帮助。

新增项目：非正式的 1 对 1 咨询会

• 1 对 1 非正式咨询会将从本周五开始，并在周六和周一继续进行。
  • 这些会议是非正式的，不用于解决课程问题。
  • 相反，这些会议是一个机会，可以与助教（通常是高年级学生）讨论学习策略、其他课程、实习、研究机会，或就伯克利的生活提出建议。
  • 这些会议不是为解决作业问题设计的，因此我们特意选择了作业截止后的时间安排。
  • 你可以通过办公室时间系统区分这些咨询会议，会议地点将显示为advising（咨询）。
  • 这些会议将在周一开放预约，并于周五、周六、周一正式举行，你可以在本周任何时间预约。

Python 表达式

Python 表达式与 print() 函数的区别

• 当你在 Python 交互式解释器中输入表达式时，它会显示该表达式的值。
• print() 函数可以显示结果，但是有区别：
  • 如果你直接输入表达式，比如输入 "go bears"，Python 会显示 'go bears'，带有引号。
  • 但是，使用 print("go bears") 时，显示结果为 go bears，没有引号。
  • 这表明打印和表达式的求值是有区别的。

None 值的特殊性

• None 表示”无”。
  • 当你直接求值 None 时，Python 不会显示任何东西。
  • 但是如果你使用 print(None)，Python 会打印出 None。

函数返回值与 None

• 如果一个函数没有明确的 return 语句，它会默认返回 None。
  • 例如定义一个没有返回值的函数 does_not_square(x)，它计算 x*x 但不返回任何值。
  • 当调用 does_not_square(4) 时，不会返回 16，而是返回 None。

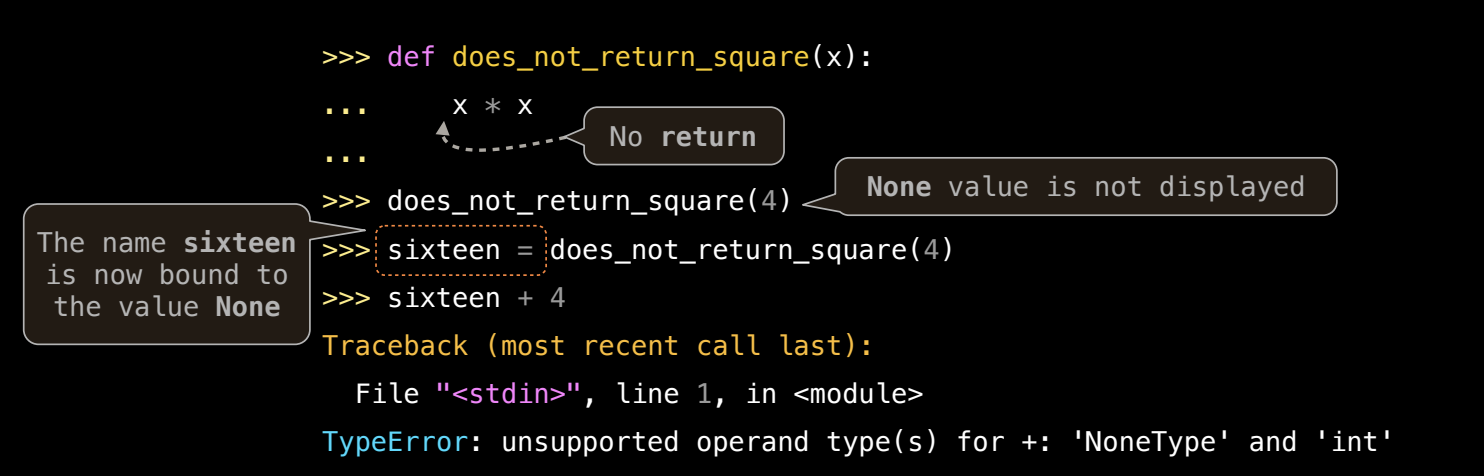
变量赋值与 None

• 如果你将 None 赋值给变量，比如 result = does_not_square(4)，那么 result 的值将是 None。
  • 如果随后执行 result + 4，会导致类型错误，因为你不能将 None 和整数相加。

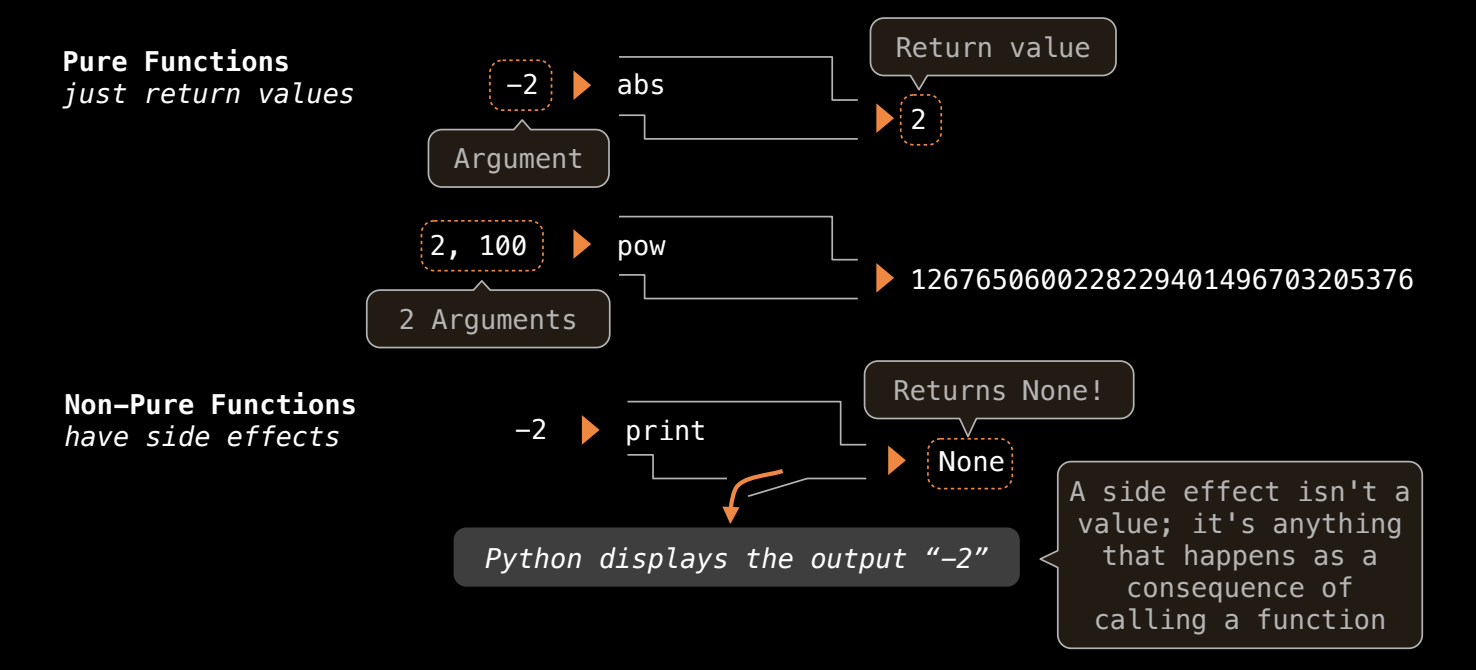
纯函数与非纯函数

• 纯函数：只依赖输入，并返回输出，没有副作用，比如 abs(-2) 返回 2。
• 非纯函数：除了返回值，还有副作用，比如 print() 函数，返回 None，同时输出内容。
  • 纯函数是一个封闭的输入输出系统，而非纯函数除了返回值，还会影响外部环境（例如打印输出）。

嵌套 print() 函数的行为

• 嵌套调用 print() 函数时，外层 print() 会输出 None，因为 print() 的返回值是 None。
  • 例如：print(print(1), print(2)) 输出 1 2 None None。
  • 通过理解 print() 的行为及其副作用，可以理解这种嵌套表达式的输出结果。

嵌套调用与表达式树

在 Python 编程中，调用函数时，尤其是嵌套调用时，理解每一步的执行过程非常重要。通过深入分析嵌套的 print() 调用，我们可以看到这种操作的复杂性。

嵌套 print() 调用的示例

print(print(1), print(2))

执行结果为：

1
2
None None

这是因为每次调用 print() 时，会产生两个不同的结果：

1. 副作用：在输出中显示传入的参数值。
2. 返回值：print() 函数总是返回 None。

分析执行步骤

1. print(1) 被首先求值，它的副作用是在屏幕上显示 1，但它返回 None。
2. print(2) 随后被求值，副作用是显示 2，返回值仍为 None。
3. 外层的 print() 函数最终打印的是两个 None 值，分别来自内部的两个 print() 调用。

表达式树分析

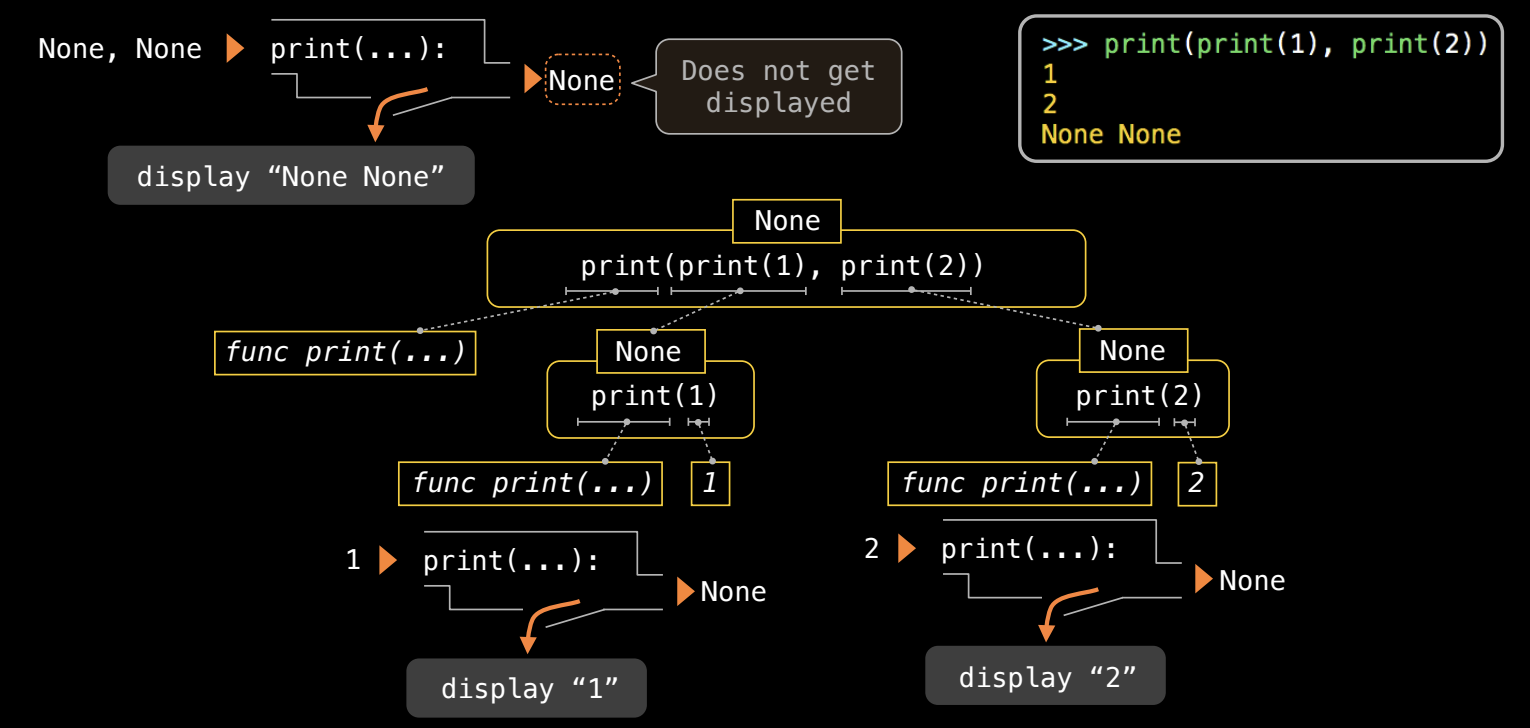
为了更好地理解嵌套函数调用的执行顺序，我们可以使用表达式树。表达式树展示了函数调用的递归结构，帮助我们直观地看到操作符和操作数的关系。

• 在表达式 print(print(1), print(2)) 中，最外层的 print() 是根节点，其子节点是内部的 print(1) 和 print(2)。
• print(1) 和 print(2) 的结果都是 None，因此外层 print() 的最终结果是 None。

用户自定义函数

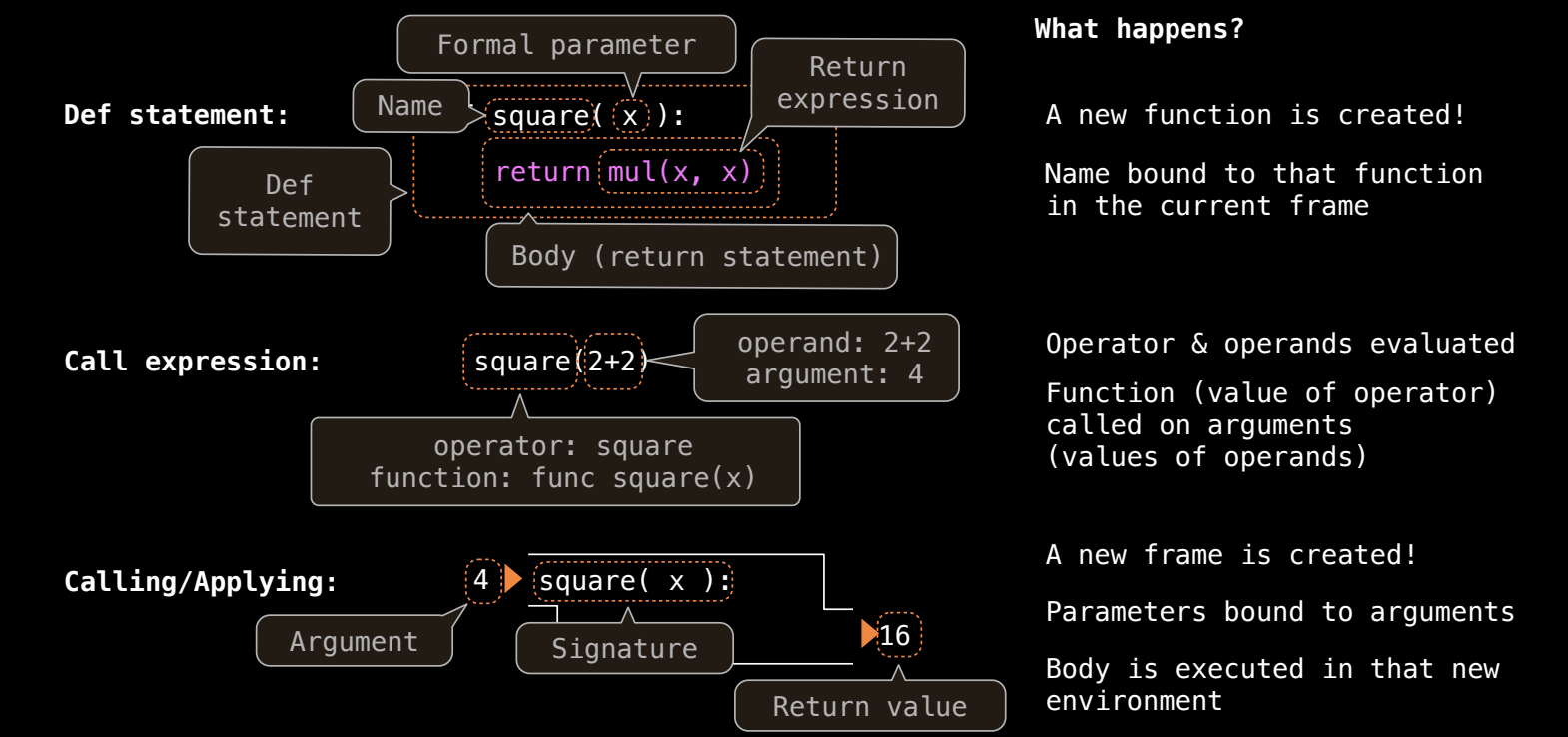
函数定义

用户自定义函数通过 def 语句来定义。一个典型的 def 语句包含以下几个部分：

1. 函数名：表示函数的名字，例如 square。
2. 参数列表：定义函数的输入，如 x。
3. 函数体：缩进的一段代码，通常包含 return 语句，用于返回计算结果。

例如，定义一个平方函数：

def square(x):
    return x * x

函数调用

调用自定义函数时，Python 按以下步骤执行：

1. 创建新帧：为函数的执行创建一个新的环境帧。
2. 绑定参数：将函数参数与实际的调用值绑定。
3. 执行函数体：在新的帧中执行函数体，最终返回结果。

例如，调用 square(4) 的步骤：

1. 创建一个新帧，并将参数 x 绑定到值 4。
2. 执行 x * x，即 4 * 4，结果为 16。

在每次函数调用时，Python 会在环境中创建一个新的帧，用来存储局部变量的绑定关系。每个环境可以包含多个帧，并且帧之间存在顺序关系。查找变量时，Python 会按照环境中的帧顺序逐一查找，直到找到变量的值。

名称在没有环境时没有意义

在编程语言中，每一个表达式都必须在特定的环境（environment）中求值。环境可以看作是一个帧的序列，存储了当前作用域中所有名称与值的绑定关系。如果没有环境，名称将无法解析出任何含义，因为它们没有与任何具体的值关联。

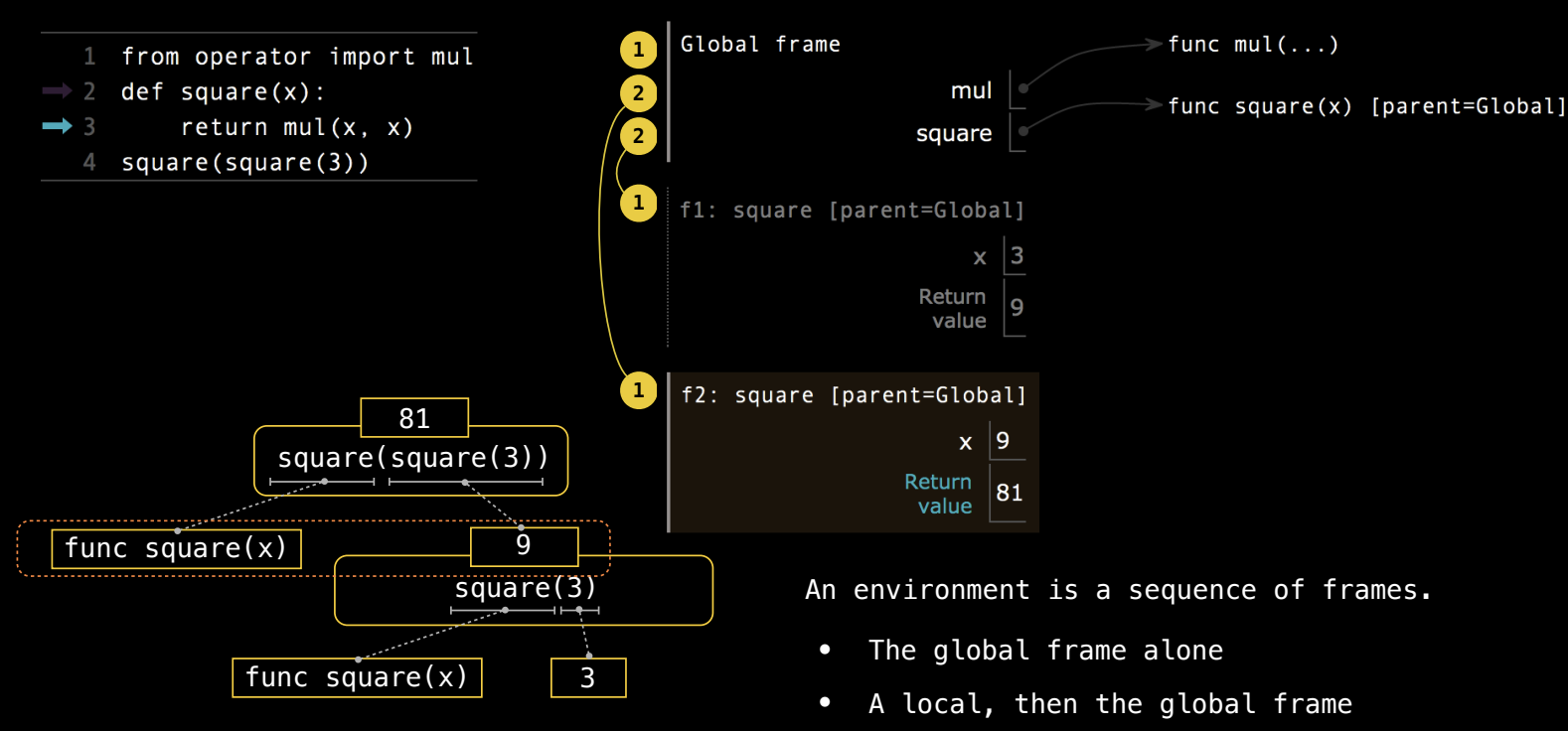
环境中的名称解析

每个名称的值是在当前环境中的某个帧里找到的。如果某个名称在局部帧中存在绑定，解释器会首先使用局部帧中的值；否则，会继续向上查找父环境中的帧，直到全局帧。

以代码 square(square(3)) 为例：

from operator import mul

def square(x):
    return mul(x, x)

square(square(3))

1. 全局帧（Global Frame）：首先，Python 会在全局帧中执行 square(square(3))。square 是在全局帧中定义的，它绑定到用户自定义的函数对象。

2. 局部帧 f1：调用 square(3) 时，解释器会创建一个新的局部帧 f1。在这个帧中，形式参数 x 被绑定到值 3。执行 return mul(x, x)，计算结果为 9，并将返回值 9 传递回全局帧。

3. 局部帧 f2：接着调用 square(9)，创建另一个局部帧 f2，此时 x 被绑定到 9。再次执行 return mul(x, x)，计算结果为 81，并将该值返回。

最终，square(square(3)) 的计算结果是 81。在整个过程中，环境图展示了局部帧如何依赖全局帧来解析函数 mul 和 square，每次函数调用都在独立的局部帧中进行。

环境是帧的序列

环境由多个帧组成，帧之间有父子关系：

• 全局帧单独存在，用于存储全局变量和函数的定义。
• 每次函数调用都会创建一个局部帧，该帧可以访问全局帧中的名称。

因此，名称的含义完全取决于它所在的环境。在不同的函数调用中，相同的名称可能绑定到不同的值。

名称在不同环境中有不同的意义

函数调用和函数体的执行在不同的环境中进行。在每次函数调用时，Python 会为函数创建一个局部帧，用来存储该调用的局部变量和参数。这意味着，即便是在相同的函数中，名称在不同调用环境下也可以有不同的含义。

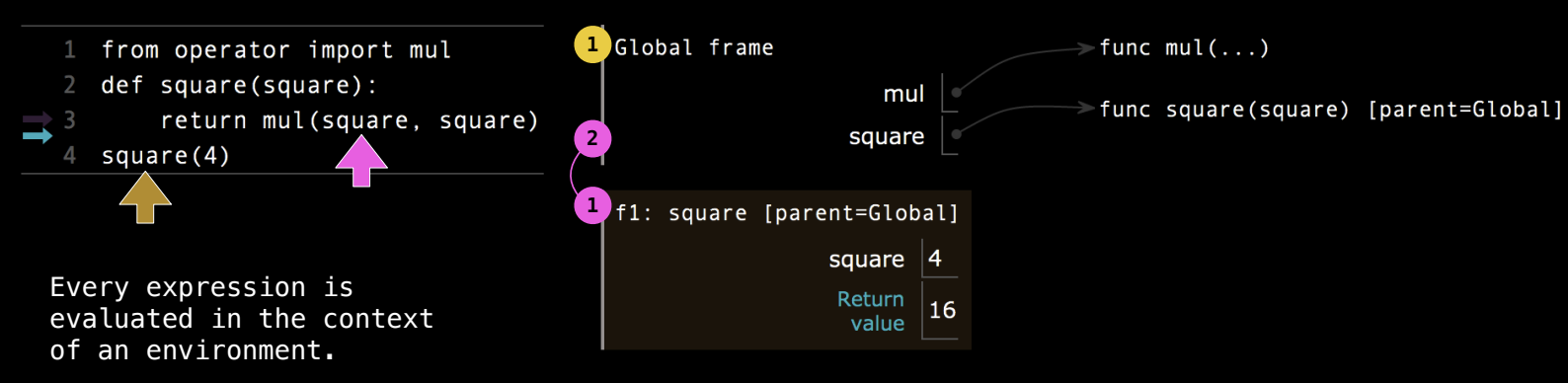
例子解析

以下代码演示了如何在不同环境中解析相同的名称：

from operator import mul

def square(square):
    return mul(square, square)

square(4)

1. 全局帧：在全局帧中，square 是用户自定义的函数，绑定到 square(square)。当执行 square(4) 时，解释器会进入全局帧，找到 square 函数，并开始调用。

2. 局部帧 f1：在调用 square(4) 时，创建了一个新的局部帧 f1。在这个帧中，局部变量 square 被绑定到实参 4。因此，尽管全局帧中的 square 是一个函数，但在局部帧中，square 现在是一个数值 4。

3. 函数体执行：局部帧 f1 中，函数体中的表达式 mul(square, square) 实际上是计算 mul(4, 4)，返回结果 16。

同名变量的不同含义

在这个例子中，局部帧中的 square 覆盖了全局帧中的 square 函数，导致函数体内的 square 绑定到局部变量 4。因此，即便全局帧中的 square 是一个函数，在局部帧中它的含义完全不同。

环境查找顺序

Python 解释器在查找名称时，遵循以下顺序：

1. 局部帧：首先在局部帧中查找名称绑定。
2. 全局帧：如果局部帧中没有找到对应的绑定，则会继续查找全局帧。
3. 内置对象：如果全局帧中也没有找到，最后查找内置的 Python 对象（例如 min、max 等）。

名称的解析始终依赖于当前的执行环境。在不同的环境中，相同的名称可以有不同的绑定。局部帧中的名称优先于全局帧中的名称，因此局部变量可以遮蔽全局变量。这种灵活的名称解析机制使得函数调用具有高度的局部性和独立性。

运算符与函数

在 Python 中，运算符（如 + 和 *）实际上是调用内置函数的简写形式。例如：

2 + 3

等价于：

from operator import add
add(2, 3)

这意味着我们可以使用运算符来进行简洁的表达式书写，同时也可以通过显式调用函数来实现相同的功能。

运算符优先级与函数调用

在 Python 中，运算符（如 + 和 *）有其内在的优先级规则。例如，乘法比加法优先执行。要改变这个优先级，可以使用括号来明确表达式的计算顺序。以下是一个例子：

2 + 3 * 4  # 输出为 14，因为乘法优先于加法
(2 + 3) * 4  # 输出为 20，括号改变了执行顺序，先进行加法运算

如果我们想将这种运算表达为函数调用形式，必须手动处理运算符的优先级：

# 相当于 2 + (3 * 4)
from operator import add, mul
result = add(2, mul(3, 4))  # 结果为 14

除法与取余

Python 中有两种主要的除法方式：

1. 真除法（True Division），使用 / 符号进行。它返回浮点数结果，例如：

   5 / 2  # 输出 2.5
   

2. 整除法（Floor Division），使用 // 符号进行。它只返回商的整数部分，忽略小数部分：

   5 // 2  # 输出 2
   

对于获取余数，Python 提供了 取模操作符（Modulus Operator） %，例如：

5 % 2  # 输出 1，表示 5 除以 2 的余数为 1

调用函数返回多个值

在 Python 中，函数可以返回多个值。例如，我们可以编写一个函数，返回商和余数：

def divide_exact(n, d):
    return n // d, n % d

quotient, remainder = divide_exact(2013, 10)
print(f"商为 {quotient}, 余数为 {remainder}")

这个函数同时返回商和余数，调用时可以使用多重赋值来获取这两个返回值。

在文件中编写 Python 代码

在实际编程中，代码通常不会直接在交互式解释器中输入，而是编写到文件中。以下是一个简单的 Python 文件示例：

# ex.py 文件
from operator import floordiv, mod

def divide_exact(n, d):
    """返回 n 除以 d 的商和余数。
    >>> q, r = divide_exact(2013, 10)
    >>> q
    201
    >>> r
    3
    """
    return floordiv(n, d), mod(n, d)

# 测试打印输出
q, r = divide_exact(2013, 10)
print(f"商为 {q}, 余数为 {r}")

在命令行中执行该文件：

python3 ex.py

编写文档字符串（Docstring）

在 Python 中，通常使用文档字符串（Docstring）来描述函数的功能。文档字符串位于 def 语句的下一行，通常用于说明函数的作用以及给出示例：

def divide_exact(n, d):
    """返回 n 除以 d 的商和余数。
    参数:
    n -- 被除数
    d -- 除数

    返回值:
    商和余数

    示例:
    >>> q, r = divide_exact(2013, 10)
    >>> q
    201
    >>> r
    3
    """
    return n // d, n % d

使用文档字符串有助于其他开发者快速理解函数的功能和用法。Python 内置的 help() 函数可以自动提取并显示文档字符串，以便开发者在使用函数时了解其细节。不仅帮助开发者理解函数的作用，还可以通过提供示例代码演示函数的使用。示例代码还可以通过 doctest 进行测试。

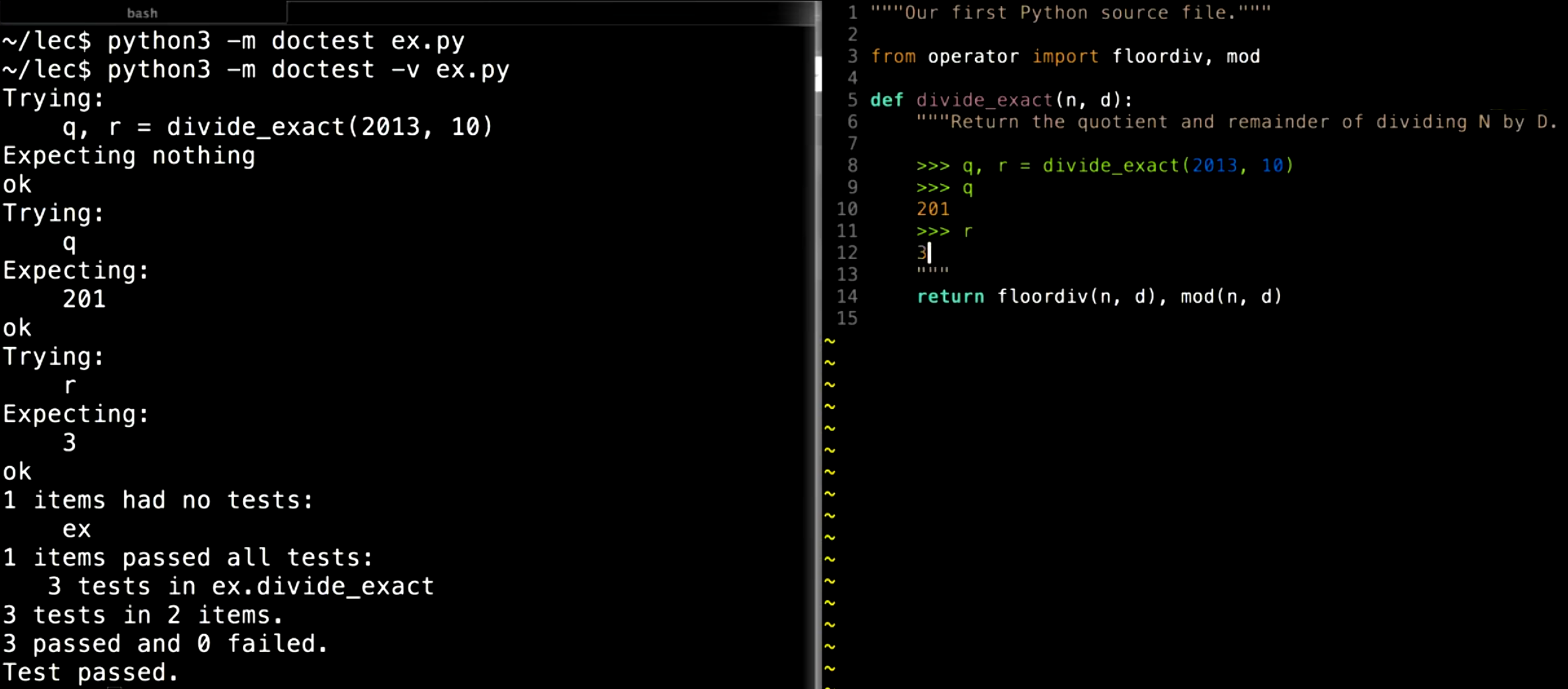
文档字符串中的代码并不是 Python 代码的实际执行部分，而是用于说明该函数的预期行为。我们可以通过 doctest 模块来测试这些示例是否按预期运行：

python3 -m doctest your_file.py

如果一切正常，控制台不会显示任何内容；如果有错误，系统会指出哪里出现了问题。

函数的默认参数值

在 Python 中，函数可以定义默认参数值。如果调用函数时没有传递对应的参数，默认值将被使用。例如：

def divide_exact(n, d=10):
    """返回 n 除以 d 的商和余数，d 的默认值为 10。"""
    return n // d, n % d

调用时可以省略第二个参数：

q, r = divide_exact(2013)
print(q, r)  # 输出: 201 3

如果传递了 d 的值，则会使用传递的值：

q, r = divide_exact(2013, 7)
print(q, r)  # 输出: 287 2

语句（Statements）

在编程语言中，语句是执行某种动作的基本单位。每条语句通过解释器执行，完成特定的操作。在 Python 中，语句可以是简单的单行操作，也可以是复杂的多行操作，这些复杂操作由多个语句组成，称为复合语句（Compound Statements）。

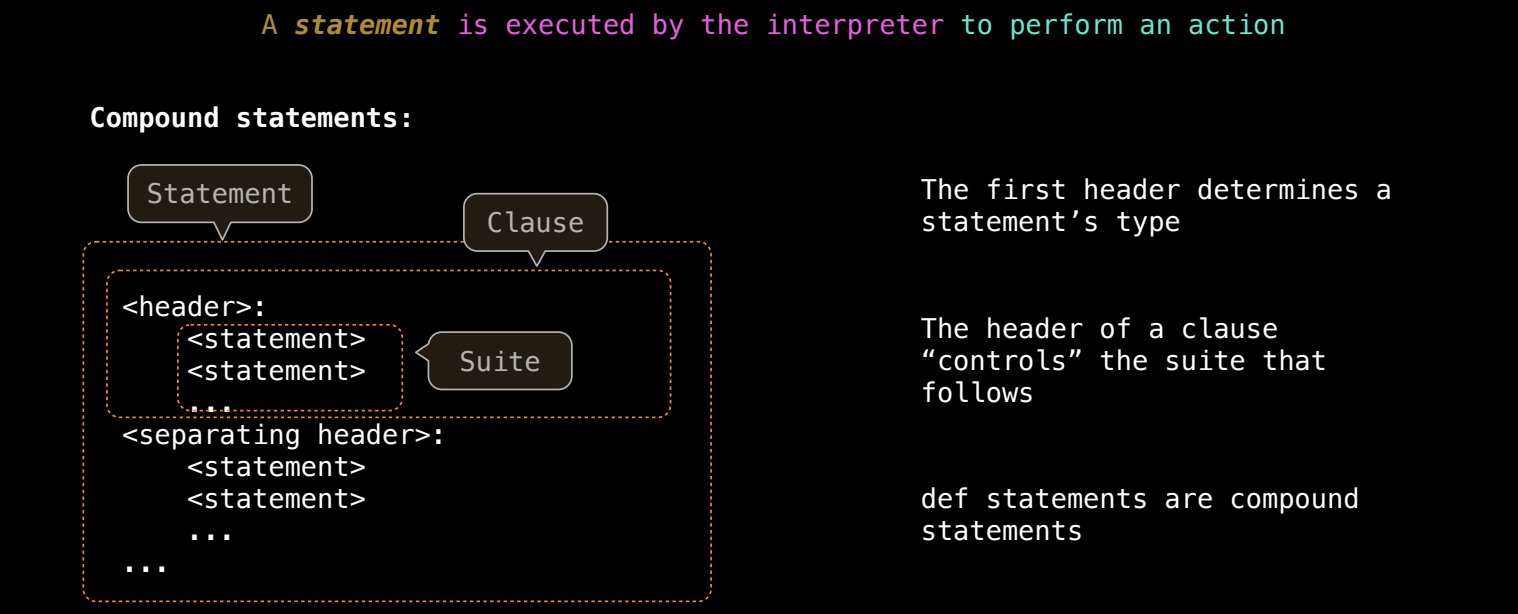
复合语句的结构

复合语句由一个头部（header）和一个或多个子句（clause）组成。每个子句包含一个语句块（suite），这个语句块由一系列语句顺序执行。

• 头部：定义复合语句的类型，例如 if、while、for、def 等语句。头部决定了后续语句的执行条件或规则。
• 子句：每个子句包含一个语句块，这些语句将按照定义的顺序执行。
• 语句块：语句块是语句的集合，当复合语句的条件满足时，语句块中的所有语句将依次执行。

在复合语句的执行过程中，解释器会按照以下规则执行：

1. 先执行第一个语句。
2. 除非有特殊指示（如跳转、循环、条件控制等），否则继续按顺序执行剩余语句。

条件语句（Conditional Statements）

条件语句用于控制程序的执行路径，根据不同条件执行不同的语句块。常见的条件语句包括 if、elif 和 else 子句。

条件语句的结构

条件语句通常包含以下部分：

• if 子句：始终是条件语句的开头部分，判断是否满足特定条件。
• elif 子句（可选）：用于指定其他可能的条件。如果 if 条件不满足，依次检查 elif 条件。
• else 子句（可选）：当所有 if 和 elif 条件都不满足时，执行 else 子句中的语句。

示例代码

def absolute_value(x):
    """返回 x 的绝对值"""
    if x < 0:
        return -x
    elif x == 0:
        return 0
    else:
        return x

在这个例子中，absolute_value 函数根据输入参数 x 的值不同，返回相应的结果。它包含：

• 1 个 if 子句，判断 x 是否小于 0；
• 1 个 elif 子句，判断 x 是否等于 0；
• 1 个 else 子句，处理所有未被 if 和 elif 覆盖的情况。

条件语句的执行规则

1. 逐个判断子句：解释器会依次检查每个子句的条件，从上到下逐条检查。
2. 执行第一个满足条件的子句：当某个子句的条件为真时，执行该子句对应的语句块，并跳过剩下的所有子句。
3. 没有条件为真时执行 else 子句：如果所有条件都不满足，执行 else 子句中的语句。

语法提示

• 条件语句总是以 if 子句开始。
• 可以有零个或多个 elif 子句。
• else 子句（如果有）总是在最后，且只有一个。

代码示例

以下代码定义了一个简单的条件语句：

def check_number(num):
    if num < 0:
        return "Negative"
    elif num == 0:
        return "Zero"
    else:
        return "Positive"

• check_number(-5) 将返回 "Negative"。
• check_number(0) 将返回 "Zero"。
• check_number(7) 将返回 "Positive"。

布尔上下文与 George Boole

布尔上下文是指程序中的那些只关心表达式是否为真的位置。在条件语句中，我们使用的表达式会根据其真值来决定后续的代码是否执行。例如，在条件判断 if x < 0 中，x < 0 就是一个布尔上下文。

在 Python 中，以下值被认为是假值：

• False
• 0（数字）
• ""（空字符串）
• None

除此之外，其他所有值都被认为是真值。

while 循环语句

Python 中的 while 语句是一种控制流程，用于反复执行一段代码，直到条件不再为真。while 循环的执行步骤如下：

1. 首先检查循环条件。如果条件为真，则执行循环体的代码块（suite）。
2. 执行完毕后，返回到第一步，再次检查条件。
3. 当条件变为假时，停止循环。

示例：累加计算

我们可以使用 while 循环来累加从 1 到 3 的数字，得到总和 6：

i = 0
total = 0

while i < 3:
    i = i + 1
    total = total + i

执行过程：

1. 初始化 i 和 total 为 0。
2. 检查 i < 3，初始为真，进入循环体。
3. 每次循环，i 增加 1，total 加上当前的 i。
4. 当 i 达到 3 时，条件 i < 3 变为假，循环结束，total 的值为 6。

代码执行流程分析

• 第一次循环时，i 变为 1，total 变为 1。
• 第二次循环时，i 变为 2，total 变为 3。
• 第三次循环时，i 变为 3，total 变为 6。此时，i < 3 不再为真，循环结束。

质因数分解算法

在这个例子中，我们要通过 while 循环来找到正整数的质因数分解。质因数分解是将一个整数分解为若干个质数的乘积。这一方法基于找到最小的质因数，逐步将数值除以该质因数，直到剩下的数值变为 1。

质因数分解的概念

每个正整数 \( n \) 都可以唯一地表示为一组质数的乘积。这些质数按照从小到大的顺序排列。例如：

• 8 的质因数分解是 \( 2 \times 2 \times 2 \)
• 9 的质因数分解是 \( 3 \times 3 \)
• 10 的质因数分解是 \( 2 \times 5 \)
• 12 的质因数分解是 \( 2 \times 2 \times 3 \)

算法思想

1. 从 \( n \) 开始，寻找最小的质因数，将 \( n \) 除以该质因数，更新 \( n \) 的值。
2. 继续寻找新的质因数，直到 \( n \) 被完全分解。
3. 这一过程可以通过循环来实现，每次找到一个最小质因数，将其从 \( n \) 中除去，直到 \( n \) 变为 1。

Python 实现步骤

首先，我们编写一个函数来实现质因数分解：

def prime_factors(n):
    """打印 n 的质因数分解"""
    while n > 1:
        k = smallest_prime_factor(n)  # 找到 n 的最小质因数
        print(k)  # 打印出质因数
        n //= k   # 将 n 除以最小质因数

在该函数中，while n > 1 保证了循环持续到 \( n \) 被完全分解。同时，我们使用了一个辅助函数 smallest_prime_factor(n) 来找到最小的质因数。

辅助函数：寻找最小质因数

接下来，我们实现 smallest_prime_factor(n)，该函数用于找到 \( n \) 的最小质因数：

def smallest_prime_factor(n):
    """返回 n 的最小质因数"""
    k = 2
    while n % k != 0:  # 循环直到找到能够整除 n 的质因数
        k += 1
    return k  # 返回最小的能够整除 n 的质因数

这里，k 从 2 开始递增，每次检查 \( n \) 是否能被 \( k \) 整除。一旦找到一个能够整除 \( n \) 的 \( k \)，我们就返回这个值。

质因数分解过程示例

让我们来一步步理解如何执行质因数分解的过程。例如，求 858 的质因数分解：

1. 初始时，\( n = 858 \)，从 2 开始寻找质因数。2 可以整除 858，因此我们找到的第一个质因数是 2，将 858 除以 2 得到 429。
2. 接下来对 429 进行同样的操作。2 无法整除 429，接下来尝试 3，3 可以整除 429，得到的质因数是 3，将 429 除以 3 得到 143。
3. 对 143，尝试从 2 开始，2 和 3 都不能整除 143，接下来尝试 11，11 可以整除 143，得到的质因数是 11，除以 11 得到 13。
4. 最后，13 是质数，因此其质因数是 13。

最终，858 的质因数分解为 \( 2 \times 3 \times 11 \times 13 \)。

完整代码

以下是质因数分解的完整代码：

def prime_factors(n):
    """打印 n 的质因数分解"""
    while n > 1:
        k = smallest_prime_factor(n)
        print(k)
        n //= k

def smallest_prime_factor(n):
    """返回 n 的最小质因数"""
    k = 2
    while n % k != 0:
        k += 1
    return k

# 测试质因数分解函数
prime_factors(858)

结果输出

运行上述代码时，结果将是：

2
3
11
13

这表明 858 的质因数分解是 \( 2 \times 3 \times 11 \times 13 \)。

质因数分解的优化与抽象

在这段代码讨论中，我们通过 while 循环编写了一个质因数分解的算法。最初，我们使用了两个函数：一个用于找到最小的质因数，另一个用于循环打印这些质因数。然而，在后续讨论中，我们尝试将这两个函数合并成一个更为紧凑的实现，并探讨了它的可读性与维护性。

代码分解与抽象的意义

将代码分为多个函数的一个重要理由是抽象化。抽象化是计算机科学中的一个核心概念，能够帮助开发者分离不同层次的逻辑，使代码更容易理解和维护。在最初的实现中，我们通过两个函数分离了 “寻找最小质因数” 和 “打印质因数” 这两个步骤。

def prime_factors(n):
    """打印 n 的质因数分解"""
    while n > 1:
        k = smallest_prime_factor(n)
        print(k)
        n //= k

def smallest_prime_factor(n):
    """返回 n 的最小质因数"""
    k = 2
    while n % k != 0:
        k += 1
    return k

优势：

• prime_factors 负责处理主要的循环逻辑和输出。
• smallest_prime_factor 专注于找到最小的质因数。

通过这种分离，我们的代码清晰地表达了不同的功能模块，便于后续的维护和修改。

合并两个函数的尝试

接下来，我们尝试将 smallest_prime_factor 的逻辑直接嵌入到 prime_factors 函数中。尽管这样减少了函数数量，但也引发了一些问题，特别是在代码的可读性和维护性上。

def prime_factors(n):
    """打印 n 的质因数分解"""
    while n > 1:
        k = 2
        while n % k != 0:  # 找到最小质因数
            k += 1
        print(k)
        n //= k  # 更新 n 的值

这种实现的确能够正确执行，但它将所有逻辑压缩在一个函数内，导致代码变得更难理解。例如，变量 k 在不同上下文中的含义不太直观，我们需要修改变量名以增强代码的可读性。即便如此，代码的逻辑依然不如初始实现清晰。

函数抽象的好处

在讨论中我们提到，使用多个函数并通过清晰的命名将不同逻辑抽象化，能够显著提高代码的可读性和可维护性。特别是当代码规模增大时，将复杂的操作分解为更小的函数模块，可以使代码更易于理解、调试和扩展。

在最初的实现中：

• smallest_prime_factor 函数专门负责寻找质因数，它的单一职责使得代码更直观。
• prime_factors 函数通过调用 smallest_prime_factor 来处理主要的循环和输出任务，遵循了“单一责任原则”。

通过保持代码的模块化设计，开发者可以轻松定位和修改特定部分的逻辑，而不必在一个复杂的函数中查找错误或进行优化。

使用函数进行抽象化 是编写清晰、易维护代码的关键。尽管在某些情况下，将多个函数合并似乎可以简化代码，但这种做法往往会降低代码的可读性和灵活性。良好的函数抽象有助于在开发中保持代码的清晰结构，增强代码的扩展性与维护性。

最终结论是，尽管可以通过不同的方法解决问题，但使用函数进行逻辑分离，通常能够让代码更加简洁明了，更适合长期的维护和开发。