Lecture 16. Mutable Functions
在这一讲中,我们探讨一个重要的概念:可变函数。可变函数是与可变数据关联的函数,这些数据会随着时间的推移而发生变化。
可变函数的介绍
一个典型的例子是银行账户的模型,它通过一个 withdraw(取款)函数来实现。这个函数每次被调用时,会根据取款金额减少账户余额,并返回剩余的余额。
def make_withdraw(balance):
def withdraw(amount):
nonlocal balance
if amount > balance:
return 'Insufficient funds'
balance = balance - amount
return balance
return withdraw
关键概念:
- 初始余额:
make_withdraw函数接收初始余额作为参数,并创建一个withdraw函数,该函数能随着取款操作不断修改账户的余额。 nonlocal声明:为了在闭包中修改外层函数(make_withdraw)中的balance变量,必须使用nonlocal关键字。
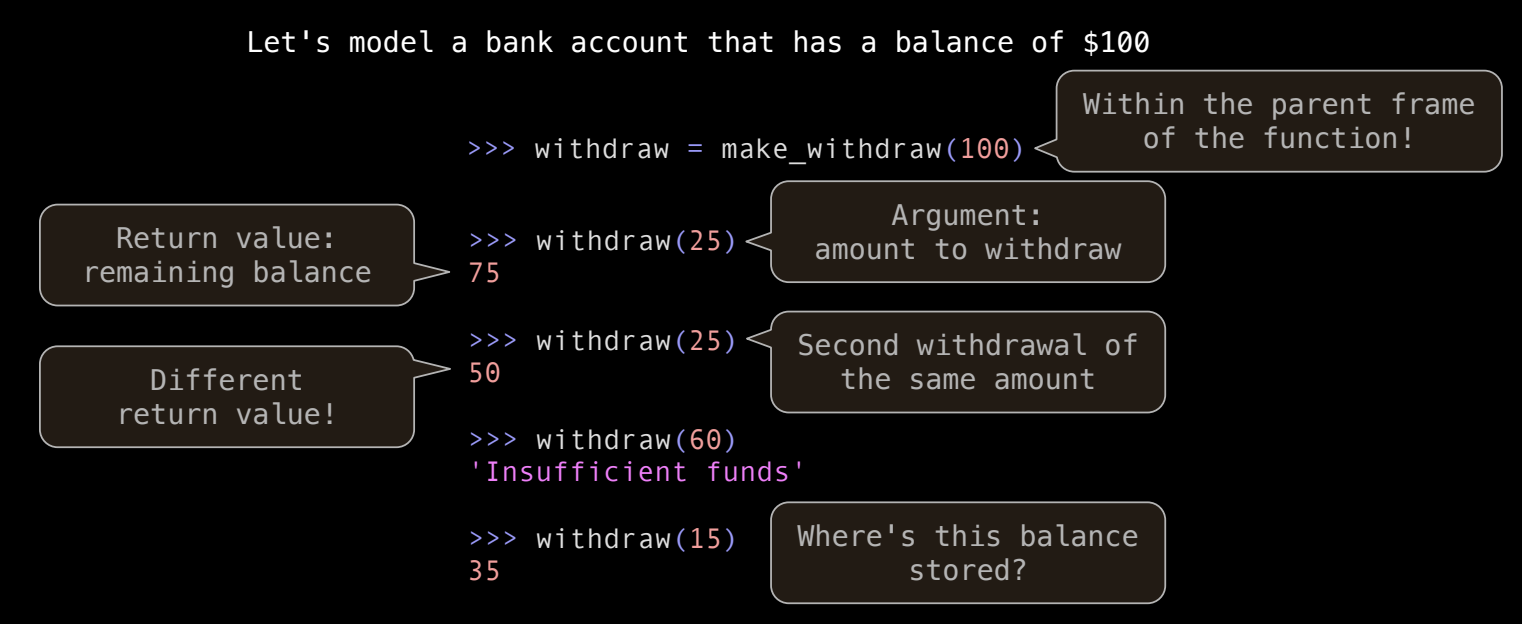
执行流程:
- 调用
make_withdraw(100),创建一个具有初始余额 100 的取款函数withdraw。 - 调用
withdraw(25),减少余额并返回 75。 - 再次调用
withdraw(25),余额减少至 50。 - 如果取款金额超出余额,例如
withdraw(60),函数会返回 “Insufficient funds”(余额不足)。
通过这种方式,withdraw 函数模拟了一个随时间推移余额会发生变化的银行账户。
环境图与变量作用域
每次调用 withdraw 函数时,都会创建一个新的调用帧,但所有这些调用帧都会共享同一个父帧(make_withdraw 的帧),从而共享相同的余额。这个共享的余额正是通过 nonlocal 声明修改的。这种设计使得函数可以维护自己的状态,并在多个调用之间保持数据的连续性。
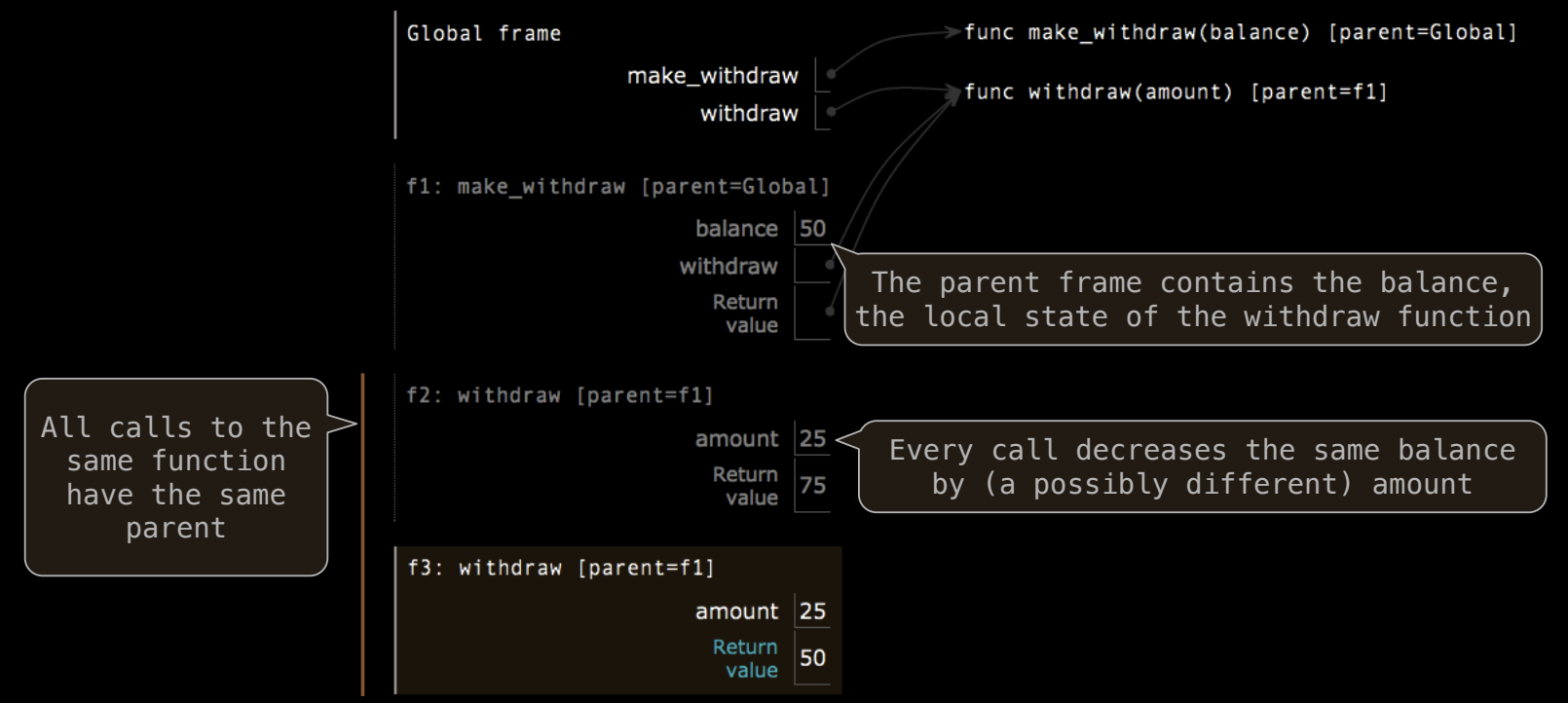
环境图解释
环境图用于帮助我们理解变量在不同作用域中的绑定与修改:
- 当
make_withdraw被调用时,会创建一个新帧,balance在该帧中绑定为初始余额。 - 调用
withdraw时,会创建一个新的帧,该帧的父帧是make_withdraw的帧。 nonlocal balance使得withdraw可以修改父帧中的balance,从而更新余额。- 余额的改变在父帧中生效,因此后续的
withdraw调用将基于更新后的余额进行计算。
非本地赋值(nonlocal)
nonlocal 赋值 是 Python 提供的一种特殊机制,它允许在嵌套函数中修改外层函数的变量。普通的赋值只能作用于当前函数的局部变量,而使用 nonlocal 可以使函数修改其外层函数中的变量。这在需要维护跨函数调用的状态时尤为重要,例如银行账户余额的动态更新。
nonlocal balance
- 这条语句告诉 Python,
balance变量并不是在当前函数中定义的,而是在外层函数中定义的,因此需要在外层作用域中进行查找并修改。
nonlocal 语句的作用
1. nonlocal 的语法
语法形式为:
nonlocal <name>, <name>, ...
2. nonlocal 语句的效果
- 作用:当使用
nonlocal声明变量时,后续对该变量的赋值会修改其在第一个非局部环境中的绑定。 - 解释:当一个变量通过
nonlocal声明后,后续对该变量的赋值会影响到其在外围函数(即“包围的作用域”或“enclosing scope”)中的值,而不是创建或修改当前函数中的局部变量。
例如:
def outer():
x = 10
def inner():
nonlocal x
x = 20 # 这将修改外层函数 outer() 中的 x
inner()
print(x) # 输出 20
在这里,nonlocal 用来修改外层函数 outer() 中的变量 x。
3. 注意
- 声明的名称必须指向包围作用域中的一个已有绑定:这意味着在
nonlocal使用之前,这个变量必须已经在外围函数中定义过。 - 声明的名称不能与当前作用域中的局部变量重名:即
nonlocal声明的变量不能与当前函数的局部变量冲突。 - 如果没有在外围作用域找到相应的变量,或者
nonlocal声明的变量和局部变量冲突,Python 将抛出SyntaxError错误。
def make_withdraw(balance):
def withdraw(amount):
if amount > balance:
return 'Insufficient funds'
balance = balance - amount
return balance
return withdraw
错误信息:
UnboundLocalError: local variable 'balance' referenced before assignment
错误的原因:
- 代码的设计意图是通过
withdraw函数不断减少balance,但在 Python 中,局部作用域中的赋值操作会将变量视为局部变量。因为balance在withdraw中被赋值(balance = balance - amount),Python 会认为balance是withdraw函数内的局部变量。 - 这会导致在
balance = balance - amount执行之前,Python 试图引用尚未赋值的局部变量balance,因此抛出UnboundLocalError错误。
解决方案
- 使用
nonlocal语句,将balance绑定到外部作用域(即make_withdraw的局部作用域)中的balance变量,而不是创建一个新的局部变量。
正确的代码示例:
def make_withdraw(balance):
def withdraw(amount):
nonlocal balance # 指定使用外部作用域中的 balance
if amount > balance:
return 'Insufficient funds'
balance = balance - amount
return balance
return withdraw
这样,内部函数 withdraw 会正确修改外部作用域的 balance 变量,避免了 UnboundLocalError。
除了使用 nonlocal,还可以通过引入可变对象来实现函数的局部状态持久化。由于列表是可变的,我们可以通过修改列表中的元素来维护函数的状态,而无需使用非本地赋值。
可变值与持久的局部状态
替代方案:使用可变对象,在不使用 nonlocal 语句的情况下,通过可变对象(例如列表)来保持局部状态。
在 Python 中,如果不希望使用 nonlocal 来改变外部函数中的不可变变量(例如整数),可以通过使用 可变对象 来达到类似的效果。
def make_withdraw_list(balance):
b = [balance] # 使用一个列表来存储 balance
def withdraw(amount):
if amount > b[0]:
return 'Insufficient funds'
b[0] = b[0] - amount # 更新列表中的元素
return b[0]
return withdraw
- 可变对象:这里使用了一个列表
b = [balance]来存储余额,而不是直接使用不可变的整数。通过修改列表中的元素(b[0] = b[0] - amount),可以实现更新余额的效果,而不需要nonlocal。 - 局部状态持久化:由于列表是可变的,内部函数
withdraw可以通过修改列表的第一个元素来更新余额。这种方法可以避免在不使用nonlocal的情况下对外部作用域中的变量进行修改。
环境图

图中的结构:
make_withdraw_list函数创建了一个列表b来存储balance。- 内部函数
withdraw修改列表中的元素来更新余额。 - 当调用
withdraw(25)时,列表b的第一个元素从100更新为75。
局部状态的变化:
- 在初始状态下,列表
b包含一个值[100]。 - 第一次调用
withdraw(25)后,b[0]被更新为75。 - 列表作为可变对象被传递给内部函数,因此即使没有
nonlocal语句,内部函数也可以通过修改列表的元素来保持外部状态的变化。
关键点
使用 可变对象(如列表、字典)可以在局部作用域中实现类似 nonlocal 的效果,允许内部函数修改外部作用域中的状态。
这种方法避免了 nonlocal 声明的需求,但需要注意的是,使用可变对象可能带来意外的副作用,尤其是在处理并发或复杂的数据结构时。
赋值语句的多种含义
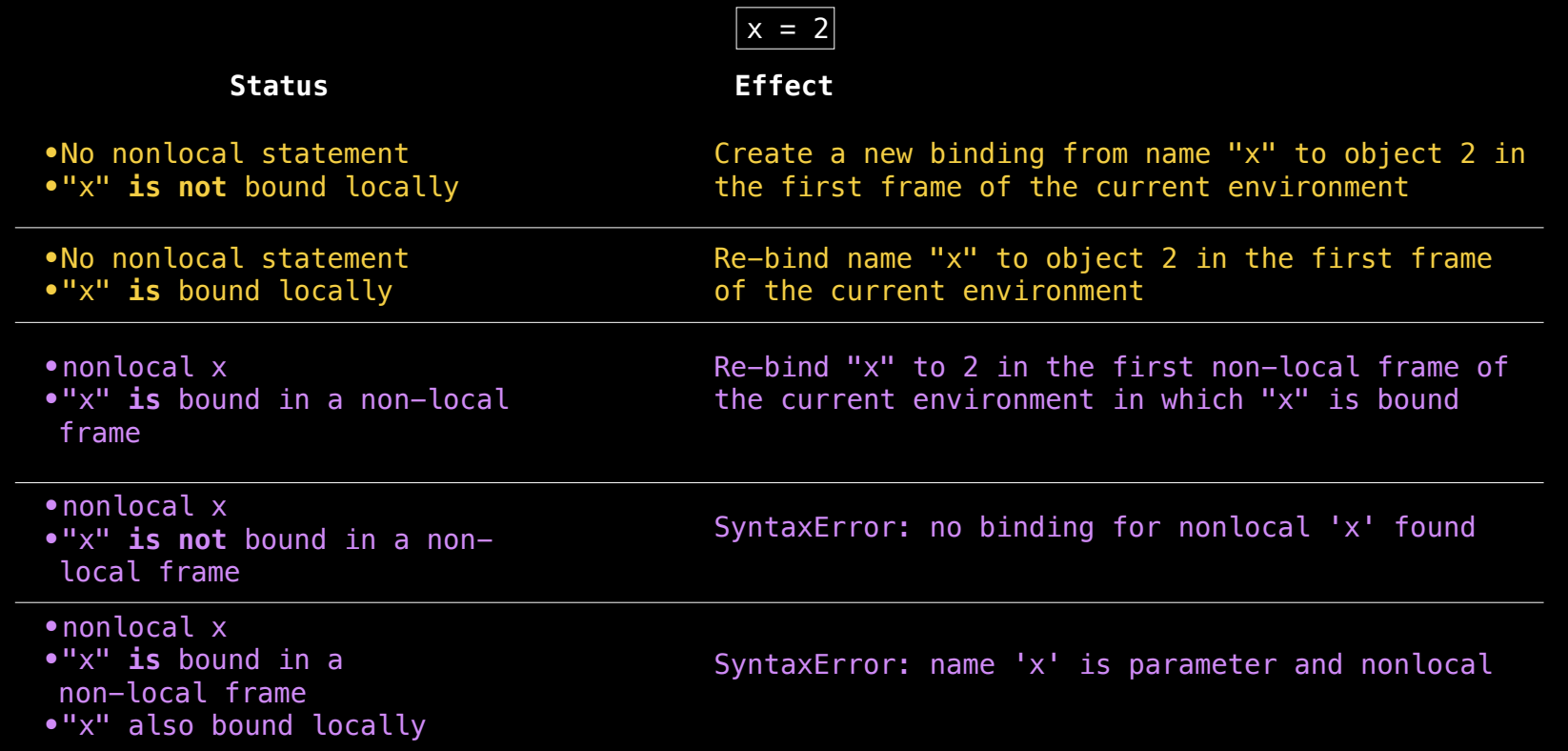
图中展示了几种情况下赋值语句 x = 2 的效果,取决于变量 x 是否绑定于局部或非局部作用域,以及是否使用了 nonlocal 语句。
1. 没有 nonlocal 声明且 x 未绑定在局部作用域中
- 状态:
x未在当前局部作用域中绑定,且未使用nonlocal语句。 - 效果:创建一个新的绑定,将名称
x绑定到当前环境中的值2。
这意味着如果 x 不存在于当前函数的局部变量中,Python 会将其作为一个新变量,并将其赋值为 2。
2. 没有 nonlocal 声明但 x 已绑定在局部作用域中
- 状态:
x已在局部作用域中存在,且没有使用nonlocal。 - 效果:重新绑定
x,将其值更新为2,而不会影响到非局部作用域中的同名变量。
这表示即使外层作用域有同名变量,局部作用域的变量不会受到影响,赋值操作只会在当前作用域中生效。
3. 使用 nonlocal x 且 x 已绑定于非局部作用域中
- 状态:
x已在非局部作用域中存在,且使用了nonlocal语句。 - 效果:重新绑定
x,将非局部作用域中的x重新绑定到2。
在这种情况下,x 的值在外围函数中被修改,而不会创建或修改局部变量。
4. 使用 nonlocal x 但 x 未绑定于非局部作用域中
- 状态:在非局部作用域中没有
x,但使用了nonlocal声明。 - 效果:抛出
SyntaxError,因为nonlocal要求x必须存在于外围的作用域中,但此时没有找到。
5. 使用 nonlocal x 且 x 在局部和非局部作用域中都已绑定
- 状态:
x已同时在局部和非局部作用域中绑定,且使用了nonlocal。 - 效果:抛出
SyntaxError,因为nonlocal语句不能和局部变量冲突。
nonlocal 声明的变量名不能与局部变量相同,否则会引发冲突并导致语法错误。
局部状态与多个可变函数
当有多个函数分别维护自己的局部状态时,它们各自的状态是独立的。我们通过一个例子来说明:
- 两个独立的银行账户:John 和 Steven 各自拥有一个独立的银行账户,John 有 $100,而 Steven 有 $100,000。
- John 和 Steven 的账户是分开的:即便他们的余额偶然相同(比如都剩下 $50),他们的账户依然是不同的。
- 每个账户的操作独立:John 的取款操作不会影响 Steven 的账户余额,反之亦然。两者各自维护自己的局部状态。
引用透明性
引用透明性 是指在一个程序中,如果用表达式的值替换该表达式,不会改变程序的行为。我们通过以下例子解释了这个概念:
mul(add(2, mul(4, 6)), add(3, 5))
当我们只有纯粹的函数调用(如加法、乘法)时,替换表达式为其计算结果不会影响程序的行为。例如,考虑以下表达式:
这个表达式是引用透明的,因为你可以逐步将子表达式替换为它们的结果,而不会改变最终结果:
mul(4, 6)计算为24。- 将
mul(4, 6)替换为24,表达式变为mul(add(2, 24), add(3, 5))。 add(2, 24)计算为26。- 将
add(2, 24)替换为26,表达式变为mul(26, add(3, 5))。 add(3, 5)计算为8,最终表达式变为mul(26, 8)。mul(26, 8)最终计算为208。
在这个过程中,每一步我们都将子表达式替换为了其值,程序的行为和含义并没有发生变化。这是引用透明性的一个例子。
然而,可变操作破坏了引用透明性。可变操作不仅返回值,还会修改程序的环境,这意味着替换一个表达式为其结果时可能会影响程序的后续执行。
引用透明性的丧失示例
我们通过一个复杂的例子展示了如何通过非本地赋值导致引用透明性丧失:
def f(x):
x = 4
def g(y):
def h(z):
nonlocal x
x = x + 1
return x + y + z
return h
return g
a = f(1) # f(1) -> g
b = a(2) # g(2) -> h
result_1 = b(3) # 调用 h(3),计算 x + y + z
result_2 = b(4) # 再次调用 h(4)
- 调用
f(1):创建一个局部变量x,初始为 1,但被立即重设为 4。返回函数g并将其赋给a。 - 调用
a(2):返回函数h,将其赋给b,此时y被设为 2。 - 第一次调用
b(3):z = 3,nonlocal x的声明使得h函数可以修改外层函数f中的x。x递增为 5,返回x + y + z = 5 + 2 + 3 = 10。
- 第二次调用
b(4):z = 4,x再次递增为 6,返回x + y + z = 6 + 2 + 4 = 12。
通过这个例子,我们展示了如何通过非本地赋值改变外层函数中的局部变量,从而导致相同的函数调用返回不同的结果。这破坏了程序的引用透明性。
总结
- 局部状态:函数的局部状态可以通过
nonlocal关键字或使用可变对象来维护。不同函数的局部状态相互独立,除非它们共享同一个可变对象。 - 引用透明性:在没有可变操作的情况下,程序中的表达式可以被其值替换而不影响程序行为。可变操作(如
nonlocal赋值)会改变程序的环境,导致引用透明性丧失。 - 可变函数与环境:通过非本地赋值和闭包,函数可以维护随时间变化的状态。这为我们提供了强大的功能,但也带来了复杂性和潜在的错误。
在设计程序时,理解引用透明性和局部状态的影响对于编写稳定且可预测的代码非常重要。
Review Problem Tree Recursion 问题
最后,课程推荐了一个递归问题 Combo,要求构建一个最小的整数,包含两个整数的所有数字。这个问题涉及 树形递归 的概念,需要通过递归寻找所有可能的组合,并选择最佳的解决方案。递归问题通常会有以下几个特点:
- 基准情况:即简单到可以直接返回结果的情况。
- 递归情况:需要通过递归调用来解决更复杂的问题。
Tree Recursion 问题:Combo
问题描述: 给定两个整数 a 和 b,需要构建一个最小的整数,包含两个整数的所有数字,且数字的相对顺序保持不变。例如,给定 a = 123 和 b = 456,你需要返回 123456,因为将所有数字组合成一个最小的数字时,这是唯一符合顺序要求的组合。
这个问题是典型的 树形递归(Tree Recursion)问题。树形递归意味着在递归的过程中,函数可能会从一个节点分支出多个递归调用,从而形成一个递归树。每个分支表示一种可能的组合。
思路和代码 (Click me after thinking!)
递归思路
1. 基准情况:
这是解决递归问题时首先要考虑的简单情况。如果我们发现其中一个数字已经用完了,那么只需要把剩下的另一个数字拼接到结果中即可。
- 基准情况:当
a或b中的数字全部用完时,直接将另一个数字剩余的部分附加到结果中。
2. 递归情况:
在递归情况中,需要递归地选择两个整数的第一个数字,将其添加到结果中。我们有两个选择:
- 选择
a的第一个数字,并递归地处理a的剩余部分和b。 - 选择
b的第一个数字,并递归地处理a和b的剩余部分。
关键点是:我们需要从两个递归选项中,选出能够生成最小数字的方案。
递归树的结构
设 a = 123 和 b = 456,递归大致如下:
combo(123, 456) (根节点)
/ \
-> 选择 '1' -> 选择 '4'
/ \
combo(23, 456) combo(123, 56)
/ \ / \
选择 '2' 选择 '4' 选择 '1' 选择 '5'
... ...
递归树显示出每个递归分支代表了两种可能的选择:一种是从 a 取第一个数字,另一种是从 b 取第一个数字。
combo(123, 456),比较 1 和 4,选择较小的数字 1,因此递归到 combo(23, 456)。递归树的另一边表示选择了 4 的情况,但因为 1 < 4,这部分被忽略了。
实际的递归路径(选择最小值的路径)
Combo(123, 456)
-> 比较 1 和 4,选择 1 (因为 1 < 4)
-> 1 + Combo(23, 456)
-> 比较 2 和 4,选择 2 (因为 2 < 4)
-> 1 + 2 + Combo(3, 456)
-> 比较 3 和 4,选择 3 (因为 3 < 4)
-> 1 + 2 + 3 + Combo(, 456)
-> 直接返回 456 (因为 a 已经为空)
=> 1 + 2 + 3 + 456 => 123456
- 所有可能的路径:递归树展示了所有可能的路径,每条路径代表着一种可能的组合方式。不同路径意味着不同的选择(比如每次选择来自
a还是b的首位数字),最终所有路径都会返回一个解。 - 实际的路径:是递归过程中程序选择的那条具体路径,也就是从根节点(初始函数调用)到一个叶子节点(递归基准条件触发,返回结果)的路径。这个路径代表了一种可能的解法。
Python 代码实现
def combo(a, b):
# 基准情况
if a == 0:
return b
if b == 0:
return a
# 转为字符串方便处理
str_a = str(a)
str_b = str(b)
# 比较第一个字符
if str_a < str_b:
# 选择 a 的第一个字符,递归处理
return int(str_a[0] + str(combo(int(str_a[1:]), b)))
else:
# 选择 b 的第一个字符,递归处理
return int(str_b[0] + str(combo(a, int(str_b[1:]))))
解释:
- 基准情况:如果
a为 0(意味着a的所有数字已经被使用),直接返回b,反之亦然。 - 递归部分:
- 将
a和b转换为字符串,比较它们的第一个字符。 - 选择较小的那个字符作为结果的第一个字符,并递归地处理剩余的字符组合。
- 将
- 最终结果:通过递归,将每个子问题的结果组合起来,返回整个拼接后的最小数字。
示例:
print(combo(123, 456)) # 输出 123456
print(combo(56, 1234)) # 输出 123456
复杂度分析:
- 时间复杂度:由于树形递归的性质,每次都有两个递归调用,因此时间复杂度近似为 O(2^n),其中
n是a和b的数字长度之和。 - 空间复杂度:递归的深度为
n,因此空间复杂度为 O(n)。
总结:
这个问题展示了树形递归的应用,通过递归地生成所有可能的组合,然后选择最小的那个结果。递归过程中,基准情况负责处理最简单的子问题,而递归情况负责将更复杂的问题分解为多个更小的子问题。