Lecture 21. Composition

Announcements

1. 作业和项目的截止日期

作业4：今天截止。
蚂蚁项目：下周五截止。需要在下周二前完成部分内容以获得检查点，加分机会是如果在下周四之前提交完整项目，将获得提前提交奖励。

2. 办公时间和问题答疑

办公室预约：下周将增加办公时间的工作人员，预约人数和答复速度将得到提升。
Piazza 答疑：更多工作人员将负责解答问题，预计比上一项目更加及时。

3. 作业5及期中考试

作业5：明天发布，截止日期为两周后的周一（26号）。作业5将帮助你为期中考试做准备。
- 实验9：将于26号（作业5截止日期）进行，唯一必做的部分是完成作业5。实验中的一些可选问题强烈推荐完成，以备考期中考试。
期中考试：在下周三（28号）进行，内容涵盖到本周五的课程。下周的课程为复习或可选内容。

树结构的复习和链表

根据匿名调查的反馈，很多同学希望有更多的树结构问题练习。因此，今天的课程将再次讨论树结构，并从面向对象的角度探讨链表的实现。

链表（Linked List）的概念与实现

链表的定义：链表要么是空的，要么包含一个值和指向剩余链表的引用。链表可以通过递归的方式定义，即每个链表的 rest 属性要么是另一个链表，要么是 Link.empty。

链表的类定义

Link 类：
- first 表示链表中的第一个值。
- rest 表示链表的剩余部分，它可以是另一个 Link 实例或者 Link.empty。
- Link.empty 是一个特殊的类属性，用于表示链表结束。

class Link:
    empty = ()
    
    def __init__(self, first, rest=empty):
        self.first = first
        self.rest = rest

链表的构造

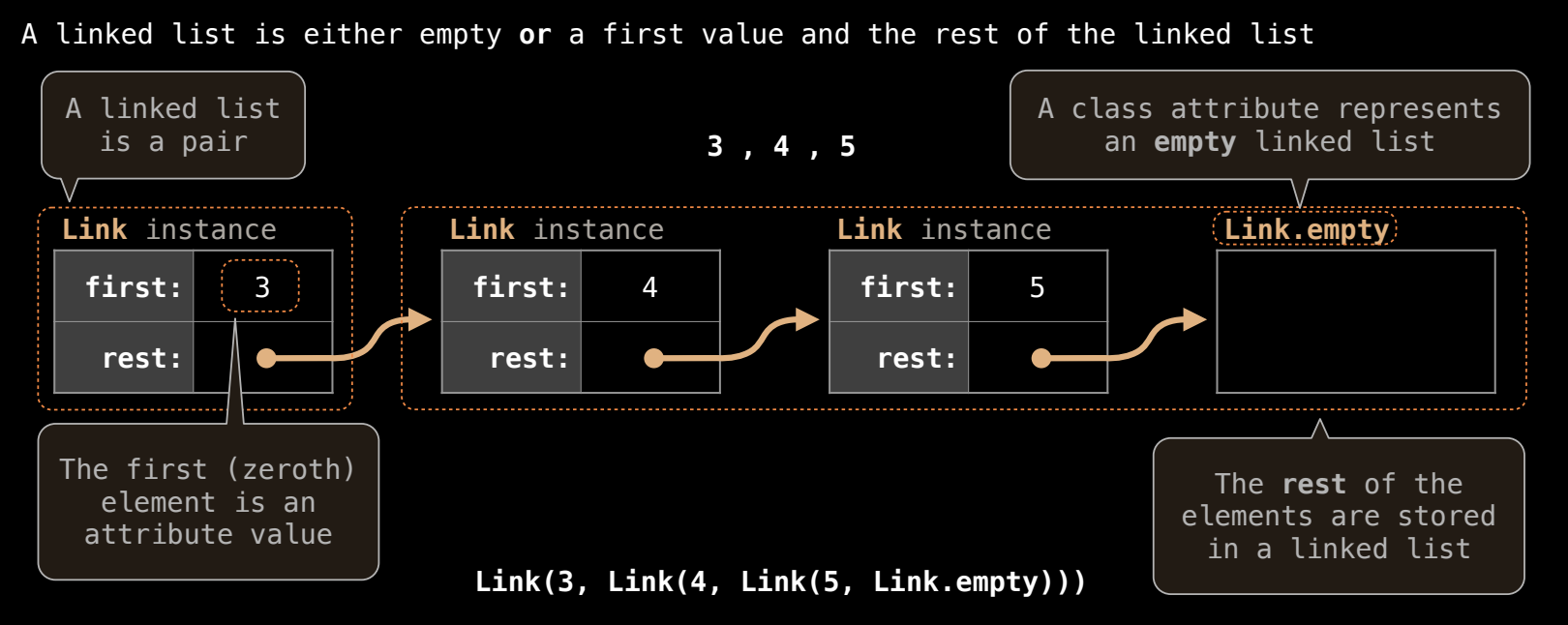
QQ_1726534369125

构造链表：例如要创建一个包含 3 -> 4 -> 5 的链表，可以按以下方式调用 Link 构造函数：

link = Link(3, Link(4, Link(5, Link.empty)))

这里，链表的构建是递归进行的。每个 Link 实例包含一个 first 值和一个 rest 链表。

链表的递归表示

递归结构：链表的 rest 可以是另一个链表或 Link.empty，实现了递归定义。例如，Link(3, Link(4, Link(5, Link.empty))) 构建的链表结构如下：
```
3 -> 4 -> 5 -> /
```
其中 / 表示链表的结束，Link.empty。

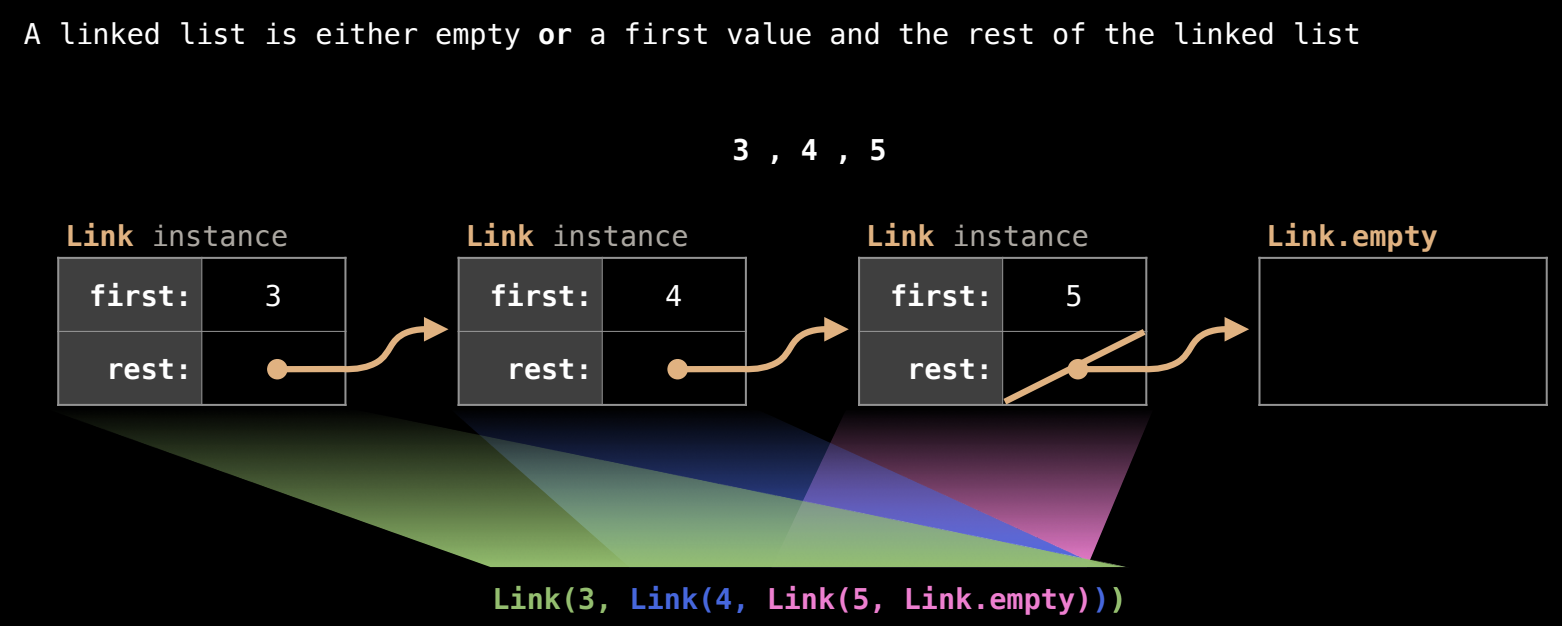
QQ_1726534493481

链表的遍历与访问

可以通过递归方式遍历链表，依次访问每个元素。要获取链表中的元素，可以递归访问 first 和 rest。

链表的示例和代码执行

代码执行顺序：当构建链表时，Python 先计算最里面的表达式（例如 Link(5, Link.empty)），然后依次向外展开，直到构建完整的链表。
链表的绘图约定：在计算机科学中，链表常通过箭头表示，Link.empty 可以简化为一个斜线 /，表示链表的结束。

link = Link(3, Link(4, Link(5, Link.empty)))
print(link.first)  # 输出: 3
print(link.rest.first)  # 输出: 4
print(link.rest.rest.first)  # 输出: 5

链表的表示与实现细节

链表的表示方式

在绘制链表时，通常将它们表示为成对的元素，通过箭头指向下一个元素。如果链表的末尾是空的，通常会用斜杠（/）表示 Link.empty，即链表的结束。

链表的类实现

在 Link 类中，我们将 rest 属性的默认值设置为 Link.empty，这使得我们在创建链表时可以省略 rest 参数。当 rest 没有传递时，链表默认认为后面没有元素。

Link.empty：我们使用一个空元组（()）来表示链表的结束符号，这代表链表已经没有更多元素。

`Link` 类的定义

Link 类的 __init__ 方法会接收两个参数：first 和 rest。rest 要么是 Link.empty，要么是另一个 Link 实例。使用 isinstance() 函数来验证 rest 是否是 Link 类的实例，确保链表结构正确。

class Link:
    empty = ()  # 表示链表的结束

    def __init__(self, first, rest=empty):
        assert rest is Link.empty or isinstance(rest, Link), "rest must be a Link or Link.empty"
        self.first = first
        self.rest = rest

链表的构造与访问

链表的构造

要创建一个包含元素 3 -> 4 -> 5 的链表，可以使用递归调用 Link 构造函数的方式：

s = Link(3, Link(4, Link(5)))

在这段代码中，链表的每个节点都包含一个 first 值和一个 rest 值，rest 要么是另一个链表，要么是 Link.empty。

链表的访问

通过访问链表的 first 和 rest 属性，我们可以遍历链表的元素。例如，要访问链表的第二个元素（值为 4），可以通过 s.rest.first：

print(s.first)  # 输出: 3
print(s.rest.first)  # 输出: 4
print(s.rest.rest.first)  # 输出: 5

链表的可变性与不变性

修改链表：链表中的值是可变的。例如，可以通过 s.rest.first = 7 修改链表中的值。
```
s.rest.first = 7
print(s.first, s.rest.first, s.rest.rest.first)  # 输出: 3 7 5
```
不变性与递归构造：链表通常用于不变数据结构的场景中，这意味着不会修改链表的元素。我们可以通过递归构造新的链表，而不修改原有的链表。例如，可以创建一个新链表，其中第一个元素为 8，后面的元素与原链表相同：
```
new_s = Link(8, s)
print(new_s.first)  # 输出: 8
print(new_s.rest.first)  # 输出: 3
```

递归处理链表的示例

链表的递归性质使得对链表的操作可以通过递归实现。以下是几个常见的递归操作示例。

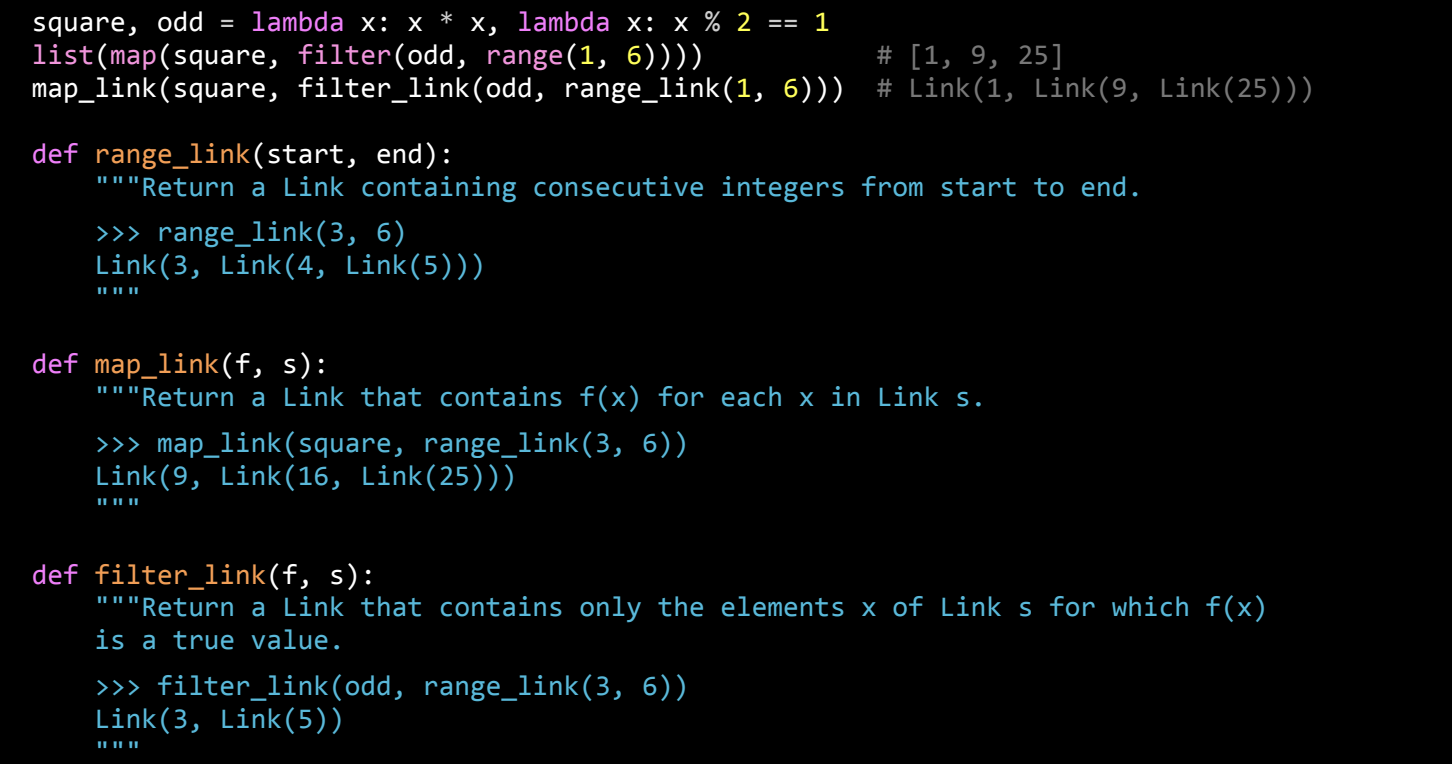
QQ_1726535023714

`range_link` 函数

range_link 函数创建一个包含连续整数的链表，从 start 到 end-1。

def range_link(start, end):
    if start >= end:
        return Link.empty
    else:
        return Link(start, range_link(start + 1, end))

# 示例：
r = range_link(3, 6)
print(r.first, r.rest.first, r.rest.rest.first)  # 输出: 3 4 5

`map_link` 函数

map_link 函数接收一个函数 f 和一个链表 s，返回一个新的链表，其中每个元素都应用了函数 f。

def map_link(f, s):
    if s is Link.empty:
        return Link.empty
    else:
        return Link(f(s.first), map_link(f, s.rest))

# 示例：
def square(x):
    return x * x

squared_r = map_link(square, r)  # 对链表的每个元素求平方
print(squared_r.first, squared_r.rest.first, squared_r.rest.rest.first)  # 输出: 9 16 25

`filter_link` 函数

filter_link 函数接收一个布尔函数 f 和一个链表 s，返回一个新的链表，只包含满足条件的元素。

def filter_link(f, s):
    if s is Link.empty:
        return Link.empty
    elif f(s.first):
        return Link(s.first, filter_link(f, s.rest))
    else:
        return filter_link(f, s.rest)

# 示例：
def is_odd(x):
    return x % 2 != 0

filtered_r = filter_link(is_odd, r)  # 过滤出奇数
print(filtered_r.first, filtered_r.rest.first)  # 输出: 3 5

链表处理的总结

链表是一种递归定义的数据结构，可以通过递归方式构建和操作。
Link 类 的实现可以通过递归的 first 和 rest 属性来表示一个序列，其中 rest 要么是另一个链表，要么是 Link.empty。
通过递归，我们可以轻松实现对链表的操作，例如 range_link、map_link 和 filter_link 等常见功能。

这种递归处理方式非常适合链表等递归数据结构，是计算机科学中数据结构操作的核心技巧之一。

链表的可变性与递归结构

链表不仅可以通过递归构建，还可以通过修改链表的属性来实现链表的变更。在 Python 中，我们可以使用属性赋值语句来改变链表中的值。例如，通过修改 first 和 rest 属性，链表中的值可以被改变。

链表的变更示例

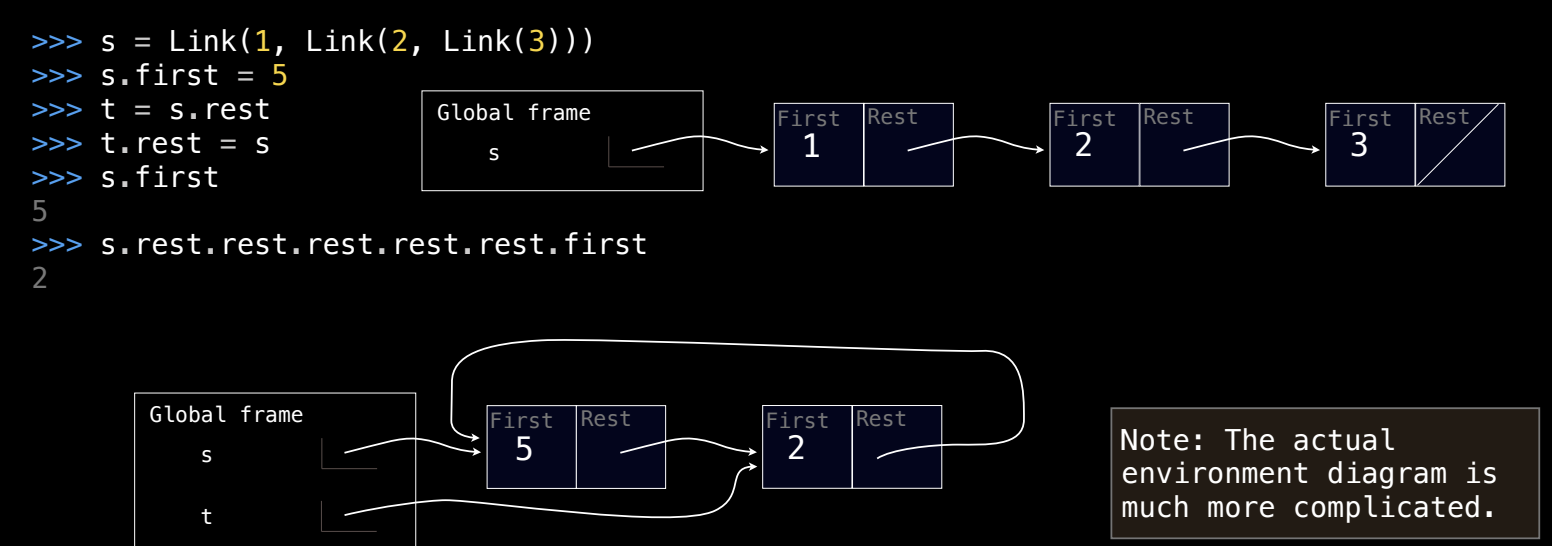
QQ_1726535586980

通过修改链表的 first 和 rest 属性，我们可以改变链表的结构。以下代码展示了如何修改链表的第一个值：

s = Link(1, Link(2, Link(3)))
s.first = 5  # 修改链表的第一个值
print(s.first, s.rest.first, s.rest.rest.first)  # 输出: 5 2 3

此外，还可以修改链表的 rest 属性，使得链表形成循环：

t = s.rest  # t 引用的是链表 s 的剩余部分 (2 -> 3)
t.rest = s  # 让 t 的 rest 指向 s，形成循环
print(s.rest.rest.rest.first)  # 输出: 5

这个例子展示了链表的递归性质，可以通过修改链表属性形成复杂的结构。

实现一个 `add` 函数

add 函数用于将一个值 v 插入到有序链表中，保持链表元素从小到大的顺序，并且不包含重复的元素。该函数会递归遍历链表，将新值插入到正确的位置。

`add` 函数实现步骤

初始条件：假设链表 s 最开始是有序的，并且没有重复元素。
递归检查：从链表的 first 开始，递归地比较 v 和每个节点的值，找到适当的位置插入 v。
插入位置：
- 如果 v 小于链表当前节点的 first，则将 v 插入链表的当前节点之前。
- 如果 v 大于当前节点的 first，递归继续遍历链表。
- 如果 v 等于链表的 first，说明 v 已经存在于链表中，不做任何修改。
末尾情况：如果遍历到链表的末尾（rest 为 Link.empty），则将 v 插入链表的末尾。

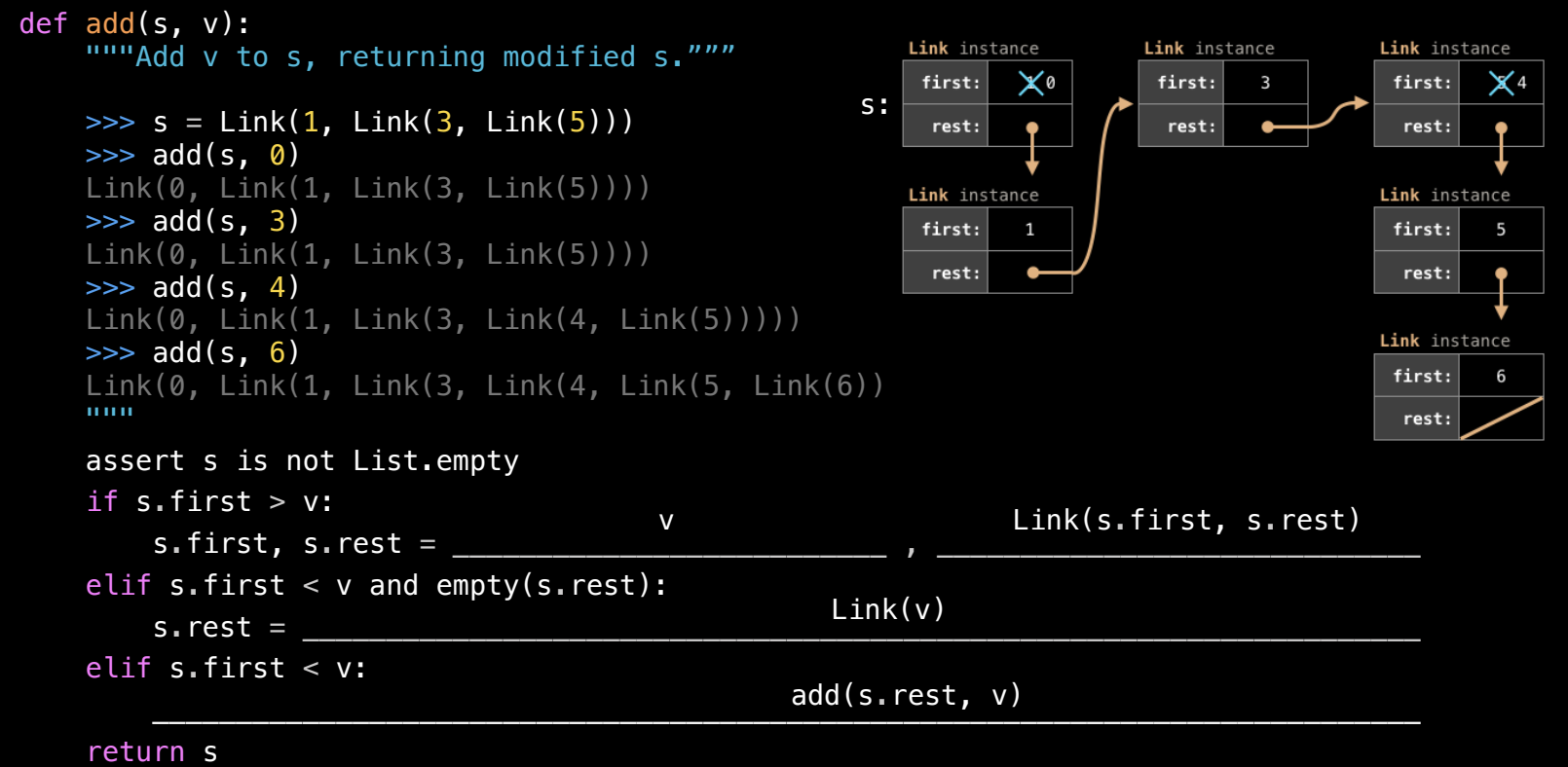
QQ_1726535644279

代码实现：

class Link:
    empty = ()  # 表示链表结束

    def __init__(self, first, rest=empty):
        self.first = first
        self.rest = rest

def add(s, v):
    # 如果 v 小于链表的第一个元素，则将 v 插入到链表的开头
    if v < s.first:
        return Link(v, s)
    # 如果 v 等于链表的第一个元素，直接返回 s，不进行修改
    elif v == s.first:
        return s
    # 如果 v 大于链表的第一个元素，但链表只剩最后一个元素，添加 v 到末尾
    elif s.rest is Link.empty:
        s.rest = Link(v)
        return s
    # 递归调用，在链表的剩余部分中插入 v
    else:
        s.rest = add(s.rest, v)
        return s

示例：

s = Link(1, Link(3, Link(5)))
s = add(s, 0)  # 在链表中添加 0
print(s.first, s.rest.first, s.rest.rest.first, s.rest.rest.rest.first)  # 输出: 0 1 3 5

s = add(s, 4)  # 在链表中添加 4
print(s.first, s.rest.first, s.rest.rest.first, s.rest.rest.rest.first, s.rest.rest.rest.rest.first)  # 输出: 0 1 3 4 5

s = add(s, 6)  # 在链表中添加 6
print(s.first, s.rest.first, s.rest.rest.first, s.rest.rest.rest.first, s.rest.rest.rest.rest.first, s.rest.rest.rest.rest.rest.first)  # 输出: 0 1 3 4 5 6

树的基本概念

树是另一种递归数据结构，与链表相似，但树的每个节点可以有多个子树。树的结构如下：

根节点（root）：树的第一个节点。
子节点（child）：从某个节点出发的其他节点。
父节点（parent）：连接到子节点的节点。
叶节点（leaf）：没有子节点的节点。

树的递归定义：

树由一个根节点和若干子树组成，每个子树也是一棵树。
如果树没有子树，它就是一个叶子节点。

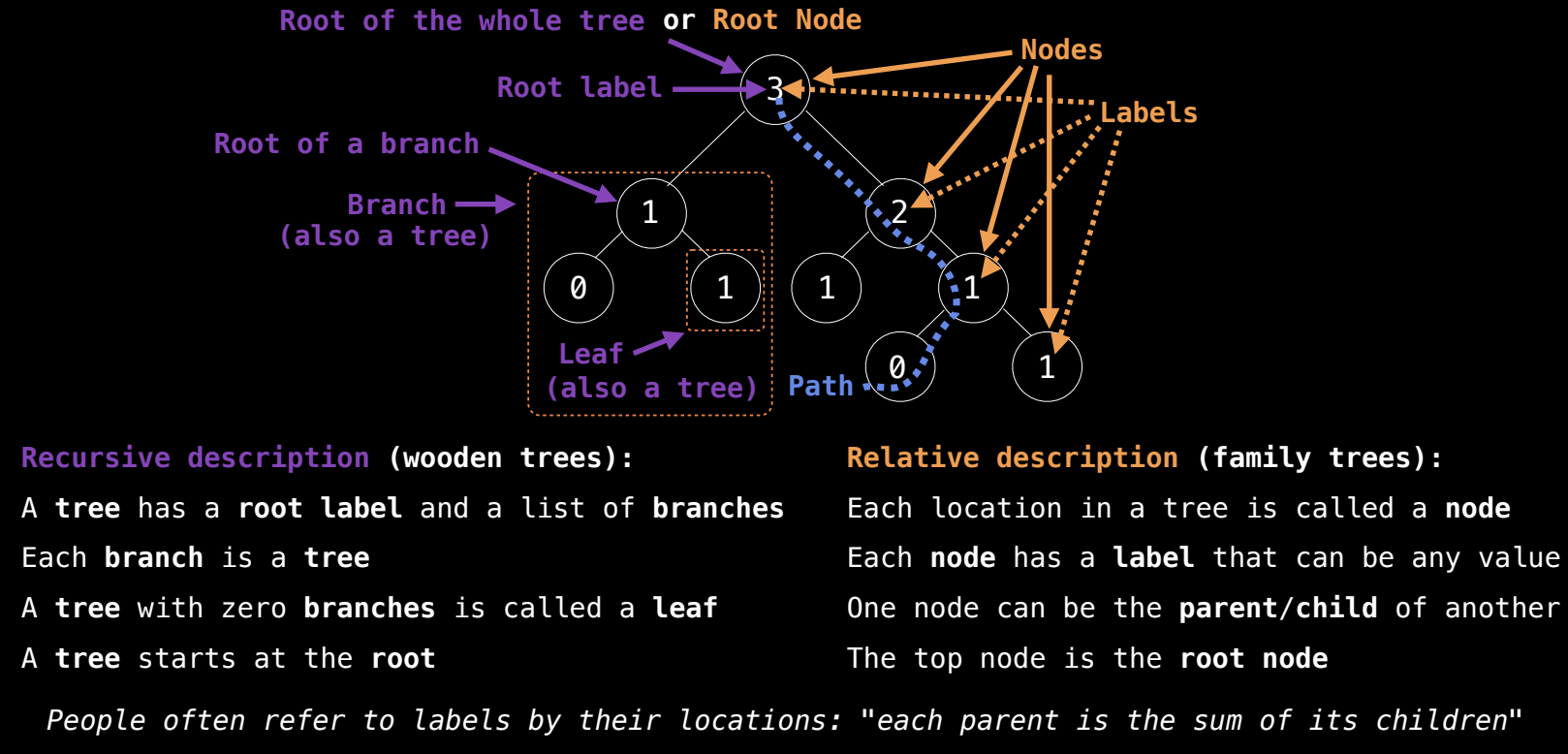
树的基本术语：

节点（Node）：树中的每个位置都可以称为一个节点。
路径（Path）：从树的一个节点到另一个节点的连接。
根到叶的路径：树中最常见的路径是从根节点到叶节点的路径。

树的关系：

父子关系：节点之间通过分支相连，连接到子树的节点称为父节点，子树的根节点称为子节点。
路径关系：节点之间可以有路径连接，路径可以从根节点开始，也可以是子树之间的连接。

树的递归处理与数据抽象

树的递归性质与链表类似，每个树都可以通过递归定义来处理。树的每个节点都包含一个标签（label），并且可能有多个分支（branches），这些分支本身也是树。可以通过递归操作对树进行处理，如遍历、查找等操作。

与链表不同的是，树可以有多个分支，这意味着树结构比链表更加复杂，适合用于表示层次结构或具有多个分支的数据。

树的定义与实现

在 Python 中，我们可以使用类来定义树。树的每个节点包含一个标签（label）和若干分支（branches），其中每个分支也是一棵树。树的定义和链表类似，但树的每个节点可以有多个分支，而链表的节点只能有一个“rest”部分。

根节点（root）：树的第一个节点，包含标签。
分支（branches）：每个根节点都有若干分支，每个分支也是树。
叶节点（leaf）：没有分支的节点。

我们可以通过定义 Tree 类来实现树的数据结构。

QQ_1726537083993

`Tree` 类的实现：

class Tree:
    def __init__(self, label, branches=None):
        self.label = label
        self.branches = branches if branches is not None else []
        # 确保每个分支都是 Tree 实例
        for branch in self.branches:
            assert isinstance(branch, Tree)
    
    def is_leaf(self):
        return not self.branches  # 没有分支则是叶子节点

    def __repr__(self):
        return f"Tree({self.label}, {self.branches})"

    def __str__(self, level=0):
        result = "  " * level + str(self.label) + "\n"
        for branch in self.branches:
            result += branch.__str__(level + 1)
        return result

__init__ 方法：接收标签和分支列表，确保分支是 Tree 实例。如果没有提供分支，默认为空列表。
is_leaf 方法：判断是否是叶节点，若无分支，则为叶节点。
__repr__ 和 __str__ 方法：用于显示树的结构。其中 __str__ 方法递归地输出树的层次结构，方便打印树的内容。

示例：

t = Tree(8, [Tree(3, [Tree(0), Tree(1)]), Tree(5, [Tree(1), Tree(1)])])
print(t)

输出的树结构如下：

self.branches = branches if branches is not None else []
这行代码使用了 Python 中的三元运算符（也称为条件表达式），它的结构是：
<值1> if <条件> else <值2>
<条件>：条件表达式 branches is not None 检查变量 branches 是否不是 None。

<值1>：如果条件为真（即 branches 不是 None），则 self.branches 被赋值为 branches。

<值2>：如果条件为假（即 branches 是 None），则 self.branches 被赋值为空列表 []。

场景说明：

在某些情况下，构造函数或方法可能允许 branches 参数为空。如果 branches 参数被传入时为 None，这行代码确保 self.branches 仍然会被赋予一个有效的默认值，即空列表 []，避免出现 NoneType 类型的错误。

如果 branches 传递了一个有效的值（比如一个列表），那这个值就会直接赋给 self.branches。

示例：
class Tree:
    def __init__(self, branches=None):
        # 设置分支，branches 是 None 时，self.branches 会变成一个空列表
        self.branches = branches if branches is not None else []

# 示例 1: 没有传递 branches 参数
tree1 = Tree()
print(tree1.branches)  # 输出：[]

# 示例 2: 传递了 branches 参数
tree2 = Tree(branches=[1, 2, 3])
print(tree2.branches)  # 输出：[1, 2, 3]

树的递归处理

与链表类似，树的递归性质使得树的处理也适合通过递归方式进行。我们可以编写函数来计算树的叶节点、树的高度等。

计算树的叶节点

我们可以递归遍历树的每个分支，并返回所有叶节点的列表。

def leaves(t):
    if t.is_leaf():
        return [t.label]  # 叶子节点返回其标签
    else:
        all_leaves = []
        for branch in t.branches:
            all_leaves.extend(leaves(branch))  # 递归添加每个分支的叶节点
        return all_leaves

示例：

leaves_of_tree = leaves(t)
print(leaves_of_tree)  # 输出: [0, 1, 1, 1]

计算树的高度

树的高度是从根节点到最远叶节点的路径中的节点数目。我们可以递归地计算每个分支的高度，取最大值并加 1。

def height(t):
    if t.is_leaf():
        return 0  # 叶节点的高度为 0
    else:
        return 1 + max(height(branch) for branch in t.branches)  # 最大分支高度加 1

示例：

height_of_tree = height(t)
print(height_of_tree)  # 输出: 2

树的 Fibonacci 示例

我们可以用树来生成 Fibonacci 序列，每个节点的标签是 Fibonacci 数，分支的标签则是两个更小的 Fibonacci 数。

`fib_tree` 函数

def fib_tree(n):
    if n == 0 or n == 1:
        return Tree(n)  # 基本情况，Fibonacci 数为 0 或 1
    else:
        left = fib_tree(n - 1)
        right = fib_tree(n - 2)
        return Tree(left.label + right.label, [left, right])  # 根为两个子树的和

示例：

fib_t = fib_tree(5)
print(fib_t)

输出的 Fibonacci 树如下：

树的其他操作：修剪（Pruning）

修剪树（Pruning）指的是移除树中某些特定条件下的子树或节点。修剪操作是递归的，首先处理当前树的分支，然后递归地修剪剩下的子树。修剪树的典型例子是根据标签的值来移除某些子树。

修剪的策略

步骤：
1. 递归处理每个分支，首先对每个分支进行修剪。
2. 然后，移除不符合条件的分支。
3. 通过修改树的 branches 属性来删除不符合条件的子树。

示例：修剪标签为 `1` 的子树

假设我们有一个树，需要移除根标签为 1 的所有子树。即所有根标签为 1 的子树都会被修剪，包括这些子树的所有后代。

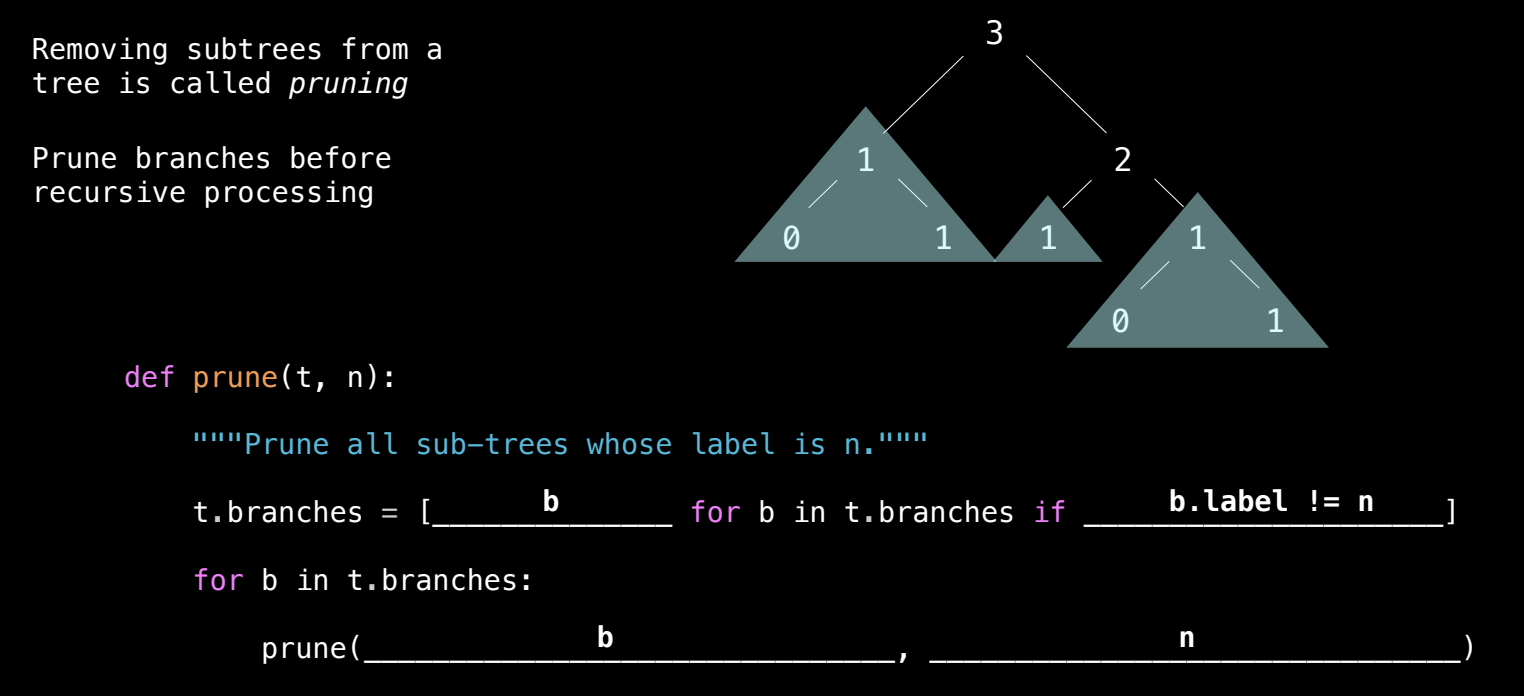
QQ_1726537060588

`prune` 函数实现：

def prune(t, n):
    # 使用列表推导式筛选出根标签不为 n 的分支
    t.branches = [b for b in t.branches if b.label != n]
    # 对剩下的分支递归调用 prune 函数
    for branch in t.branches:
        prune(branch, n)

功能描述：
- 首先，使用列表推导式来构建新的 branches 列表，只保留根标签不等于 n 的分支。
- 然后，递归地对剩余的每个分支继续进行修剪。
- 该函数不返回新值，直接修改传入的树对象。

t = Tree(8, [Tree(3, [Tree(1), Tree(0)]), Tree(5, [Tree(1), Tree(2)])])
print("Before pruning:")
print(t)

prune(t, 1)  # 移除标签为 1 的子树

print("After pruning:")
print(t)

在修剪前，树的结构如下：

修剪后，树的结构如下：

t.branches = [b for b in t.branches if b.label != n]：这行代码通过列表推导式创建了一个新的 branches 列表，其中只保留了标签不为 n 的分支。
递归调用 prune(branch, n)：对于剩下的每个分支，递归地调用 prune 函数，继续检查其子树并移除符合条件的分支。

Lecture 21. Composition

Announcements

1. 作业和项目的截止日期

2. 办公时间和问题答疑

3. 作业5及期中考试

树结构的复习和链表

链表（Linked List）的概念与实现

链表的类定义

链表的构造

链表的递归表示

链表的遍历与访问

链表的示例和代码执行

链表的表示与实现细节

链表的表示方式

链表的类实现

Link 类的定义

链表的构造与访问

链表的构造

链表的访问

链表的可变性与不变性

递归处理链表的示例

range_link 函数

map_link 函数

filter_link 函数

链表处理的总结

链表的可变性与递归结构

链表的变更示例

实现一个 add 函数

add 函数实现步骤

代码实现：

示例：

树的基本概念

树的递归定义：

树的基本术语：

树的关系：

树的递归处理与数据抽象

树的定义与实现

Tree 类的实现：

示例：

场景说明：

示例：

树的递归处理

计算树的叶节点

计算树的高度

树的 Fibonacci 示例

fib_tree 函数

树的其他操作：修剪（Pruning）

修剪的策略

示例：修剪标签为 1 的子树

prune 函数实现：

`Link` 类的定义

`range_link` 函数

`map_link` 函数

`filter_link` 函数

实现一个 `add` 函数

`add` 函数实现步骤

`Tree` 类的实现：

`fib_tree` 函数

示例：修剪标签为 `1` 的子树

`prune` 函数实现：