Lecture 29. Calculater
Announcements
本周的作业(Homework 6)将于今天截止,而作业 7 将在明天发布,并于下周四截止。作业主要是一些 Scheme 相关的问题。此外,期中考试 2 的重新评分申请截止到下周一。同时,课程即将发布 Project 4,虽然这个项目相比以往稍微简化了一些,但接下来你可能会变得更忙,因为我们将开始讨论更复杂的话题。
今天的讲座与 Project 4 密切相关,因为你将在这个项目中构建一个 Scheme 解释器。我们将开始两次讲座,专门讲解如何为编程语言设计解释器。解释器是一个程序,它接受编程语言中的代码作为输入,并执行这些代码,进而产生程序所描述的行为。
编程语言与解释器
在本课程中,我们讨论了 Python 和 Scheme。我们学习 Scheme 的原因有两个:
- Scheme 是一种简洁有效的编程语言,尽管简单但功能强大,今天仍然在项目中使用。
- Scheme 规则少且灵活,你可以通过编写 Python 程序来实现 Scheme 的解释器。
解释器是将编程语言的语句、表达式解释执行的程序。在解释器的工作过程中,程序的语法结构往往以树的形式组织,解释器通过树递归的方式来解析和执行代码。这种结构让解释器可以处理多层嵌套的表达式,逐步将每个子表达式执行并返回结果。
解释器的工作原理
解释器的输入是另一个程序,而这个程序可以被视为一种高阶函数。解释器通过模块化的方式工作:一部分解释器负责解释语言的通用规则,另一部分负责执行具体的语法结构和表达式。例如,解释器需要知道如何处理变量、函数调用以及控制流结构(如条件判断和循环)。
编程语言的层次
计算机通常使用多种编程语言来执行程序,包括:
- 机器语言:这是计算机硬件直接执行的语言。每个计算机的中央处理单元(CPU)都可以执行一组固定的指令,操作硬件中的内存地址。这种语言难以编程,因为它没有抽象机制,不能使用变量或函数。
- 高级语言:Python 和 Scheme 就是高级语言,它们提供了抽象机制,可以为值、函数、对象和类命名。高级语言比机器语言易于编程,因为它们隐藏了底层硬件的细节。
在现代计算机系统中,通常有一个编译器或解释器将高级语言转化为低级的机器语言。例如,Python 在执行之前会被编译成字节码,然后由 Python 解释器执行这个字节码。
解释器与编译器
- 解释器:读取并逐行执行程序。Scheme 和 Python 通常都是解释执行的。
- 编译器:将整个程序翻译成机器语言,然后交由计算机执行。C 语言通常通过编译器生成机器码。
有时,现代编程语言使用两者结合的方式。例如,Python 会将程序编译为字节码,然后再通过解释器执行。
高级语言的优势
高级语言让编程更容易,因为它们提供了强大的抽象工具,帮助程序员更轻松地解决问题。它们还抽象了硬件的细节,使得程序可以在不同的硬件和操作系统上运行。例如,Python 解释器可以在 Windows、macOS 和 Linux 上运行,而不需要修改 Python 代码。
Python 的字节码
在 Python 中,代码在执行前被编译成字节码(bytecode)。字节码是一种低级语言,介于高级语言和机器语言之间。你可以使用 Python 的 dis 模块查看编译后的字节码。然后,Python 解释器会执行这些字节码,这个过程类似于执行机器语言,但仍然保留了一定程度的系统抽象。
课程的整体思路
本课程的重点是理解编程语言的工作原理以及如何设计解释器。你将学习如何从零开始构建一个 Scheme 解释器,通过树递归解析程序中的语句和表达式,逐步实现语言的各种特性。这不仅能帮助你深入理解编程语言的构造,还能为后续学习编译器设计和更多高级编程概念打下基础。
创建编程语言的流程
编程语言的创建和使用涉及到多个复杂的过程,包括语法和语义的设计与实现。每种编程语言都有其独特的语法(合法语句和表达式的形式)和语义(执行和求值的规则)。无论是用于并发编程的 Erlang,还是用于生成静态网页的 MediaWiki 标记语言,每一种语言的成功应用都依赖于清晰的语法和语义,以及合适的解释器或编译器的实现。
要创建一门新的编程语言,通常有两种途径:
- 形式化规范:为语言编写详细的文档,描述其语法和语义。规范明确规定了语言的合法输入以及如何执行这些输入。
- 实现解释器或编译器:通过实现一个解释器或编译器来定义语言的行为。合法的语法是在不导致程序崩溃的情况下能够被解释器或编译器正确处理的输入,语义则由程序对这些输入的处理结果定义。
例如,Scheme 最早是通过形式化规范定义的,之后才实现了其解释器。而 Python 则相反,它首先实现了一个解释器,之后才逐渐发展出正式的规范。
解析器的工作原理
解析(parsing)是将程序的源代码文本转化为计算机可以处理的表达式的过程。解析器通过以下步骤完成:
-
词法分析(Lexical Analysis):将源代码分割为一系列标记(tokens)。每个标记可以是关键字、操作符、数字、变量名等。词法分析的任务是识别这些标记,并过滤掉无关的内容,比如空格和注释。
-
语法分析(Syntactic Analysis):语法分析器根据词法分析生成的标记序列,将它们组织成层次化的结构,例如抽象语法树(AST)。这个过程验证标记是否按正确的语法规则组合在一起,并构建出能被解释器或编译器处理的结构。
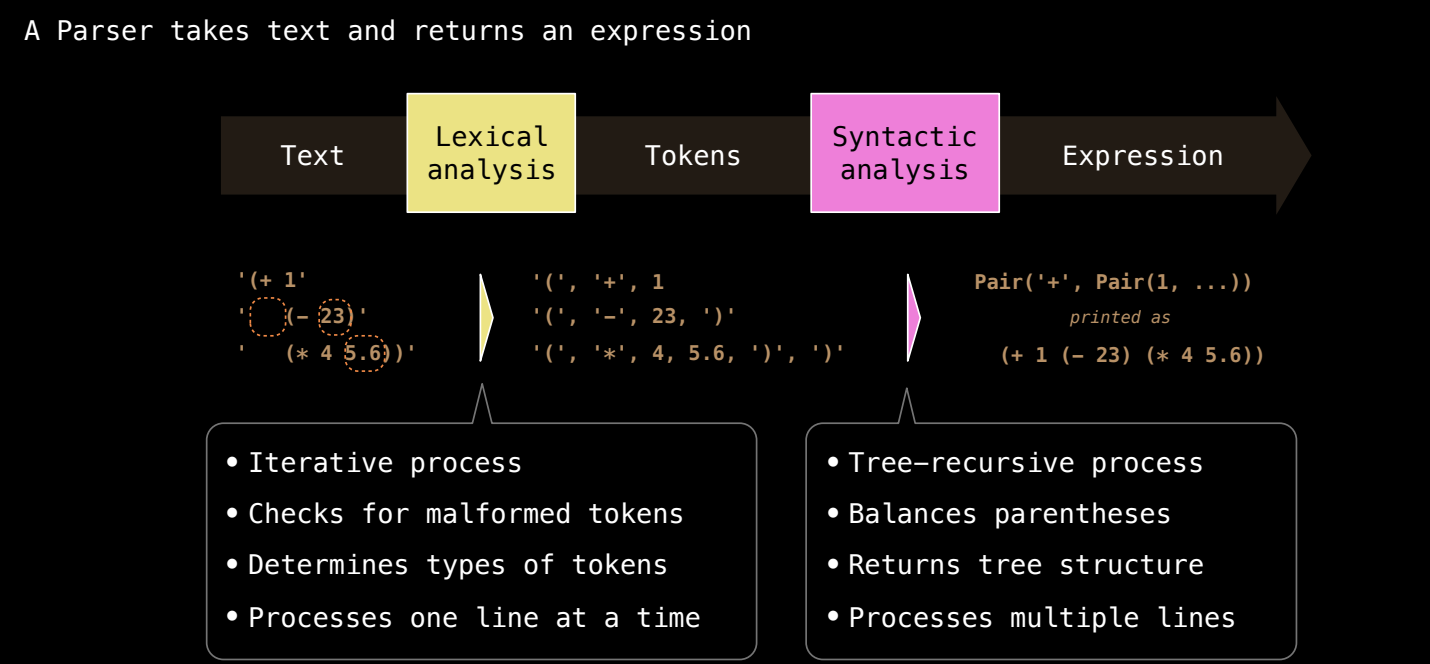
解析示例
假设输入代码如下:
(+ 1
(- 2 3)
(* 4 5.6))
解析过程如下:
- 词法分析:
- 第一步是将每一行拆分成标记。例如,第一个括号和
+操作符是两个标记,而1是一个数字标记。 - 空格被忽略,
2和3作为-操作符的参数是单独的标记。 4和5.6也是单独的标记,5.6是一个浮点数。
- 第一步是将每一行拆分成标记。例如,第一个括号和
词法分析的输出可能是如下标记序列:
'(' '+', '1', '(', '-', '2', '3', ')', '(', '*', '4', '5.6', ')', ')'
- 语法分析:
- 语法分析器将这些标记组织成一个结构化的表达式。对于这个例子,解析结果是一个嵌套的表达式树:这个表达式树的根节点是
+,它有三个子节点:数字1,子表达式(- 2 3)和子表达式(* 4 5.6)。
- 语法分析器将这些标记组织成一个结构化的表达式。对于这个例子,解析结果是一个嵌套的表达式树:这个表达式树的根节点是
词法分析与语法分析的结合
词法分析器和语法分析器是解析过程中的两个主要组件。词法分析器的作用是将程序文本转化为标记,语法分析器则负责将这些标记组合成一个抽象的表达式,供解释器或编译器进一步处理。词法分析器在识别标记的过程中会执行一些预处理,比如忽略空格和注释、识别数字和操作符。而语法分析器则负责检查表达式的结构是否符合语言的语法规则。
递归下降解析器
递归下降解析器(Recursive Descent Parser)是一种简单但强大的解析方法,它通过递归函数调用来解析输入的编程语言表达式。每个解析步骤会检查输入的标记(token),并根据标记的类型决定如何处理该部分的表达式。对于 Scheme 这样的语言,解析器主要关注以下几点:
- 基本元素(如数字或符号):这些是递归解析的基本情况。
- 组合(combination):当遇到左括号
(时,意味着我们遇到的是一个组合(包含多个子表达式的表达式)。解析器将递归解析组合内部的所有子表达式,直到遇到右括号)。
解析 Scheme 表达式的过程
以以下 Scheme 表达式为例:
(+ 1 (- 2 3) (* 4 5.6))
解析的流程如下:
- 词法分析:首先将表达式分解为标记:
(,+,1,(,-,2,3,),(,*,4,5.6,),)
词法分析会将源代码分解为这些标记,忽略空格,并将数字(如
5.6)视为一个整体。 - 语法分析:通过递归解析构建嵌套的表达式树。以
(+ 1 (- 2 3) (* 4 5.6))为例,解析器首先识别+是一个组合的操作符,并继续递归解析其余的子表达式:1是一个基本元素。(- 2 3)是一个嵌套的组合,解析器递归处理它。(* 4 5.6)同样是一个嵌套组合。
最终,解析器生成的结构是一个嵌套的树状结构:
(+ 1
(- 2 3)
(* 4 5.6))
递归下降解析器的实现
在 Scheme 的解析过程中,scheme_read 函数负责处理输入的标记并返回相应的表达式。这个函数通过递归调用自身来解析嵌套的组合表达式。其伪代码结构如下:
def scheme_read(tokens):
if len(tokens) == 0:
raise SyntaxError("Unexpected EOF")
token = tokens.pop(0)
if token == '(':
sub_expressions = []
while tokens[0] != ')':
sub_expressions.append(scheme_read(tokens))
tokens.pop(0) # Remove closing ')'
return sub_expressions
elif token == ')':
raise SyntaxError("Unexpected )")
else:
return parse_atom(token) # Parse numbers or symbols
代码解释
- 词法分析:首先将输入分解为标记序列。
- 语法分析:当遇到左括号
(时,表示一个新的组合开始。解析器递归调用自身来解析每个子表达式,直到遇到右括号)为止。 - 基本元素处理:如果遇到数字或符号,它们会被直接返回(通过
parse_atom函数进行处理)。
递归下降解析器的优点
递归下降解析器的一个重要特性是,它通常只需要检查有限数量的标记来决定接下来如何处理。这意味着它可以通过一次递归下降来构建整个表达式树,而不需要向前看太多标记。这种 预测递归下降解析器(Predictive Recursive Descent Parser)在某些编程语言(如 Scheme)中非常高效,因为它们的语法规则相对简单。
Scheme 计算器的基本结构
我们现在将讨论如何创建一个简单的编程语言——Scheme 语法计算器(Scheme Syntax Calculator),它可以像计算器一样执行基本的算术运算。这是一个简单的例子,用于展示如何通过 Python 来实现一个 Scheme 解释器。我们将通过解析、语法树和递归处理,来评估 Scheme 表达式。
这个计算器的功能是解析和计算 Scheme 表达式,它支持四种基本运算:加法、减法、乘法和除法。输入的 Scheme 表达式会被解析为一个由 Pair 类 表示的树结构,然后通过递归方式计算其值。
Pair 类
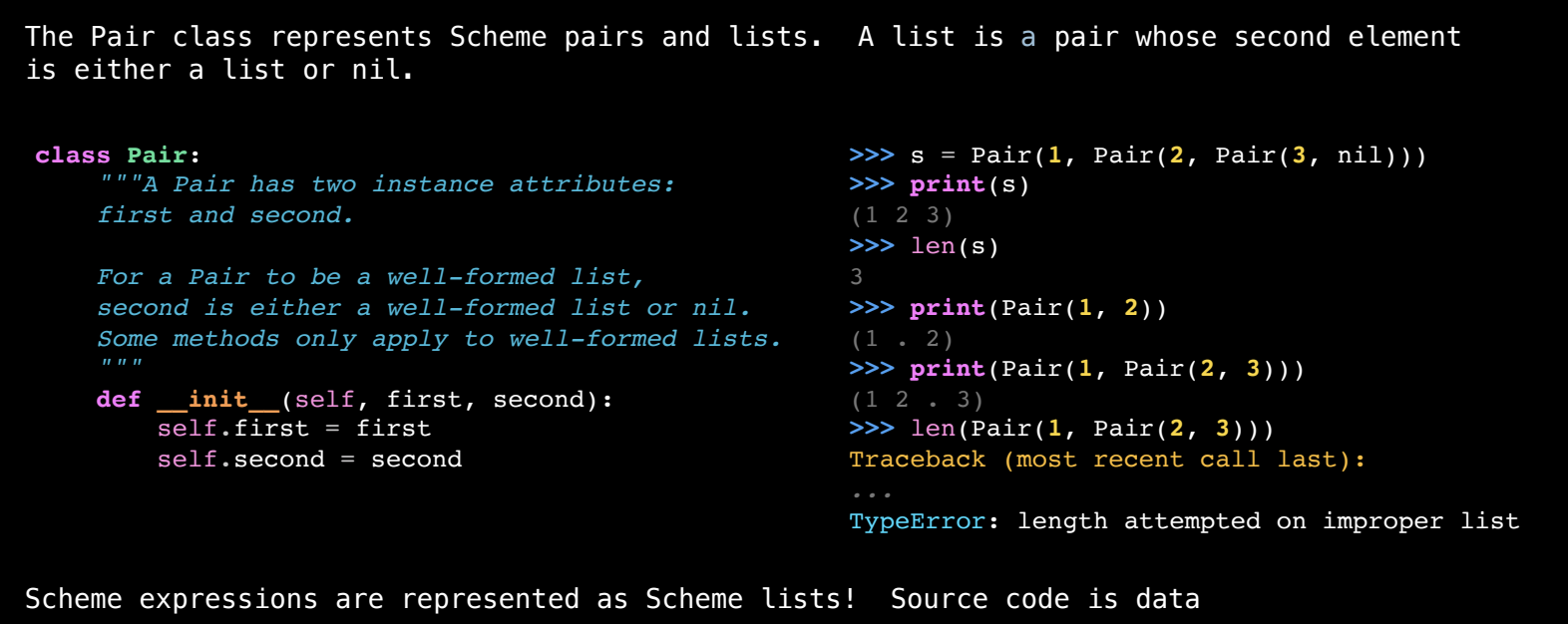
在 Scheme 中,所有的表达式都可以用 Pair 类来表示,特别是列表和组合表达式。Pair 类的两个属性是 first 和 second,分别代表一个表达式的第一个元素和剩余部分。如果 second 是另一个 Pair 或 nil,则它表示一个 Scheme 列表。
class Pair:
def __init__(self, first, second):
self.first = first
self.second = second
# 其他与列表相关的方法,例如计算长度和打印格式化的 Scheme 表达式
在这种设计下,Pair 类既可以表示普通的 Scheme 列表,也可以表示不规则的(非“良好”形式的)对。例如,(1 . 2) 是一个“点对”(dotted pair),而 (1 2 3) 是一个“良好形式”的列表。
表达式解析与表示
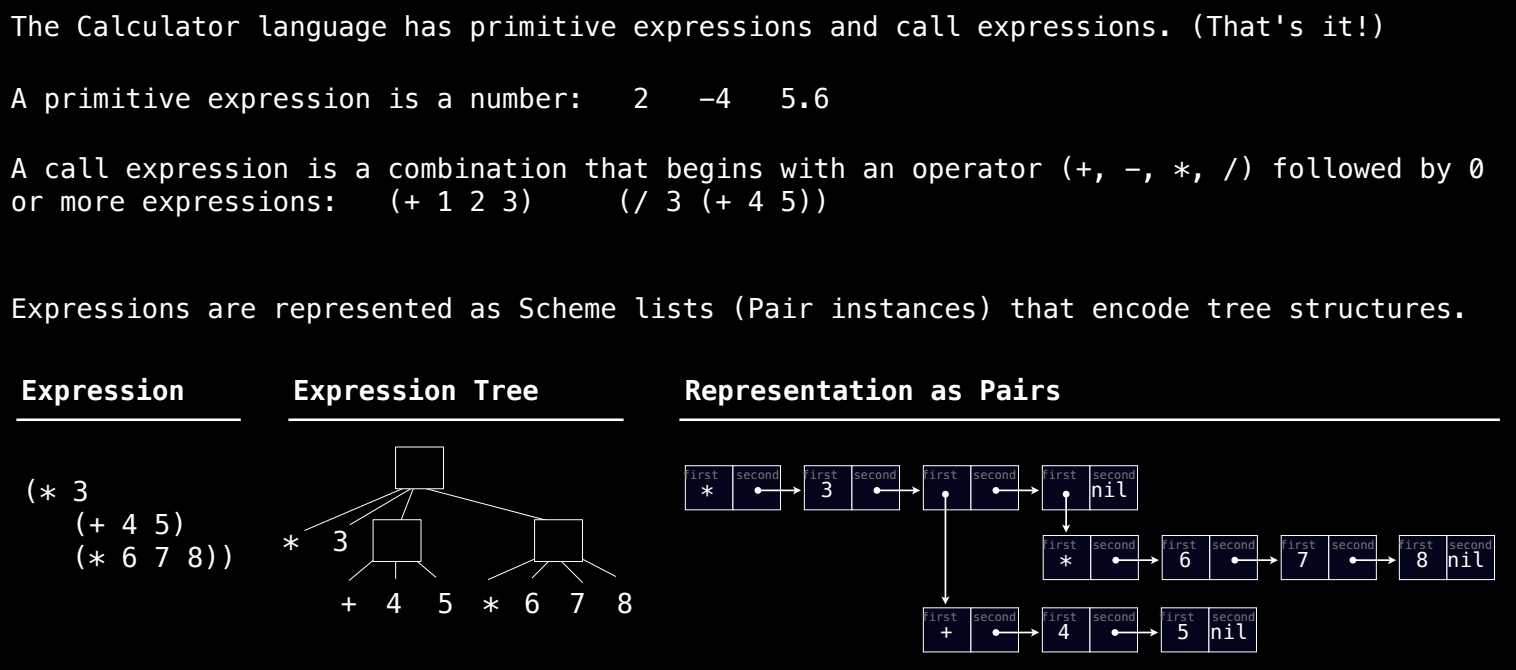
Scheme 的表达式可以用树结构表示。每个操作符(例如 +、- 等)都是树的根节点,操作数是该节点的子节点。这个树结构通过 Pair 类来表示。例如,表达式:
(* 3 (+ 4 5) (* 6 7 8))
可以表示为一棵树,其中 * 是根节点,子节点分别是 3、(+ 4 5) 和 (* 6 7 8)。
在我们的解释器中,表达式会被解析为类似以下结构的 Pair 对象:
(* 3 (+ 4 5) (* 6 7 8))
表示为:
Pair('*', Pair(3, Pair(Pair('+', Pair(4, Pair(5, nil))), Pair(Pair('*', Pair(6, Pair(7, Pair(8, nil)))), nil))))
语法与语义
语法 定义了语言中的合法表达式。在这个简单的计算器语言中,我们只允许两种表达式:
- 基本表达式:数字。
- 调用表达式:以操作符(
+、-、*、/)开头,后跟零个或多个表达式。
语义 则定义了如何计算这些表达式的值:
- 基本表达式:数字直接返回其自身的值。
- 调用表达式:首先递归计算所有操作数的值,然后将这些值传递给操作符来进行计算。
示例表达式:树状结构
考虑表达式:
(* 3 (+ 4 5) (* 6 7 8))
它的树状结构表示为:
*
/ | \
3 + *
/| /|\
4 5 6 7 8
该表达式的评估过程如下:
- 首先计算
+ 4 5,得到9。 - 计算
* 6 7 8,得到336。 - 计算最终表达式
* 3 9 336,结果为9072。
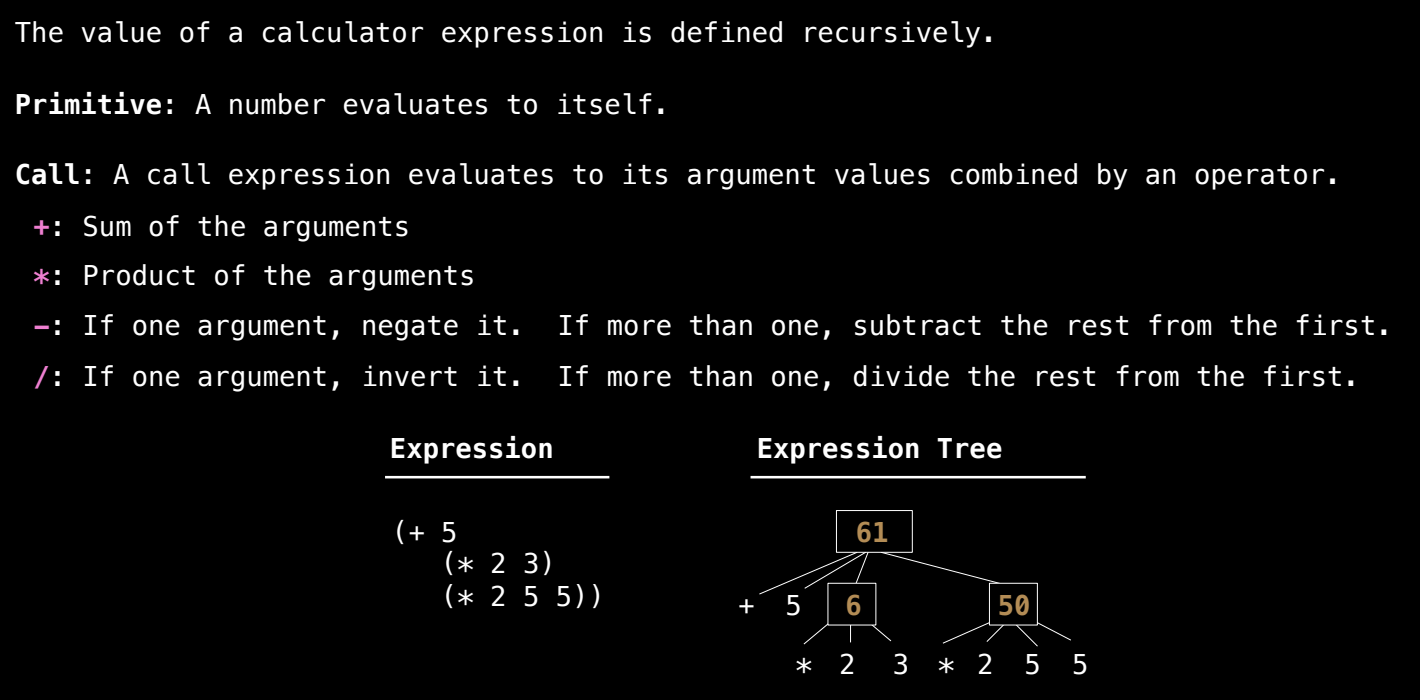
递归评估表达式
为了实现这个计算器,我们需要递归评估表达式。基本步骤如下:
- 基例:如果是数字,直接返回该数字。
- 递归处理:如果是调用表达式,先递归求值操作数,然后根据操作符进行相应的运算。
用户输入示例
在计算器中输入如下表达式:
(* 3 (+ 4 5) (* 6 7 8))
计算器会解析并生成相应的树状结构,并递归计算每个子表达式,最后输出 9072。
Evaluation
计算器语言的核心部分
-
calc_eval函数:
该函数负责评估输入的表达式。它会根据表达式的类型决定如何处理:
- 如果表达式是一个数字(整数或浮点数),直接返回它的值。
- 如果表达式是一个组合(调用表达式),首先递归地评估每个子表达式,然后应用运算符进行计算。
def calc_eval(expr): if isinstance(expr, (int, float)): # 基本表达式,数字 return expr elif isinstance(expr, Pair): # 调用表达式 operator = expr.first operands = expr.second arguments = operands.map(calc_eval) # 递归评估操作数 return calc_apply(operator, arguments) -
递归评估操作数: 通过递归的方式处理表达式树,
calc_eval函数调用自身来处理子表达式,直到每个操作数都被简化为一个数字。例如,给定表达式(* 3 (+ 4 5) (* 6 7 8)),解释器首先会递归评估(+ 4 5)和(* 6 7 8),得到9和336,然后将它们与3一起乘,得出最终结果9072。 -
calc_apply函数: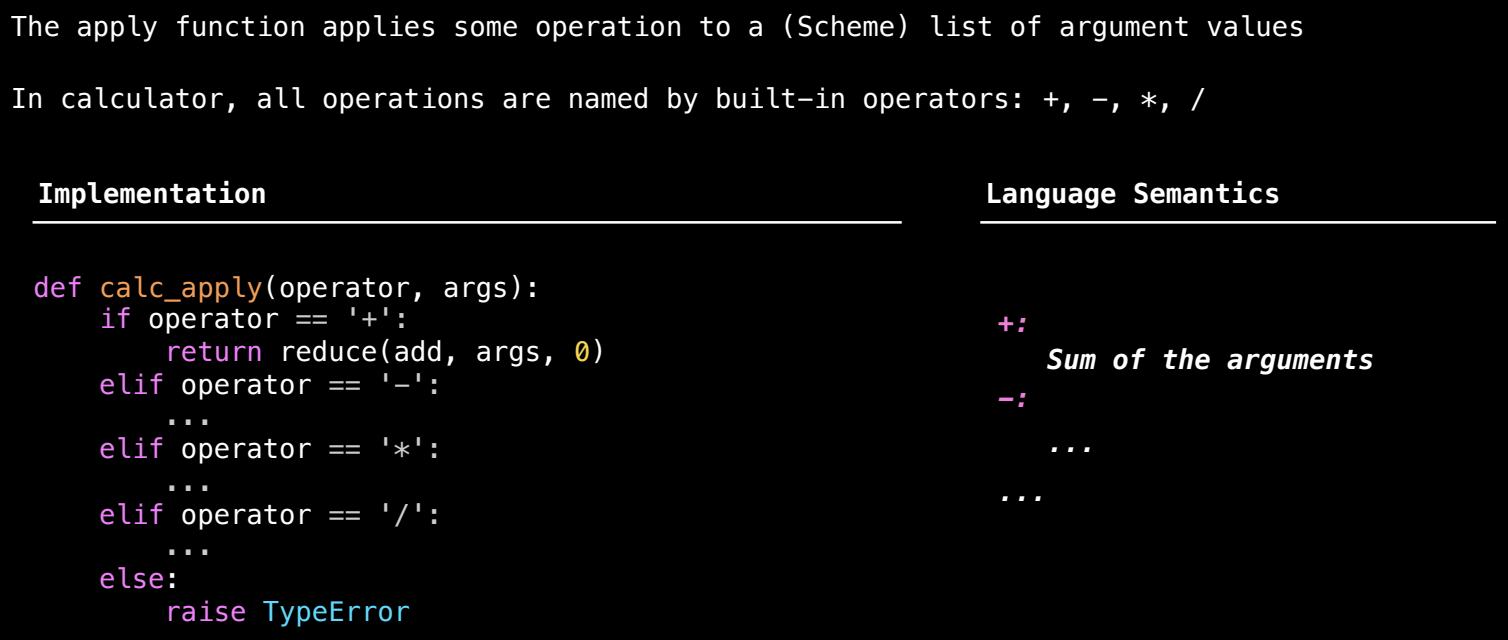
这个函数负责将运算符应用于一组操作数。计算器只支持四个运算符(
+、-、*、/),因此calc_apply会根据操作符的不同选择相应的计算方式。def calc_apply(operator, arguments): if operator == '+': return sum(arguments) # 加法 elif operator == '-': if len(arguments) == 1: return -arguments[0] # 一元减法 return arguments[0] - sum(arguments[1:]) # 多个操作数的减法 elif operator == '*': result = 1 for arg in arguments: result *= arg # 乘法 return result elif operator == '/': if len(arguments) == 1: return 1 / arguments[0] # 一元除法(求倒数) result = arguments[0] for arg in arguments[1:]: result /= arg # 多个操作数的除法 return result
运算符的处理逻辑
每个运算符的处理方式如下:
- 加法(
+):将所有操作数相加。 - 减法(
-):如果只有一个操作数,则返回该数的相反数;如果有多个操作数,则从第一个操作数中减去后续所有操作数。 - 乘法(
*):将所有操作数相乘。 - 除法(
/):如果只有一个操作数,则返回它的倒数;如果有多个操作数,则从第一个操作数开始,依次进行除法操作。
例子
考虑以下表达式:
(* 3 (+ 4 5) (* 6 7 8))
(+ 4 5)通过递归调用calc_eval被简化为9。(* 6 7 8)通过递归调用calc_eval被简化为336。- 然后
(* 3 9 336)被计算,结果是9072。
错误处理
我们还可以在解释器中添加一些简单的错误处理机制,例如:
- 如果遇到一个无效的运算符,抛出类型错误。
- 如果
calc_apply中的运算符不是预期的+、-、*或/,则返回错误消息。
def calc_apply(operator, arguments):
if not isinstance(operator, str):
raise TypeError(f"'{operator}' is not a valid operator")
if operator == '+':
return sum(arguments)
elif operator == '-':
if len(arguments) == 1:
return -arguments[0]
return arguments[0] - sum(arguments[1:])
elif operator == '*':
result = 1
for arg in arguments:
result *= arg
return result
elif operator == '/':
if len(arguments) == 1:
return 1 / arguments[0]
result = arguments[0]
for arg in arguments[1:]:
result /= arg
return result
else:
raise TypeError(f"Unknown operator: {operator}")
解释器的用户界面:REPL 循环
我们已经讨论了如何通过递归实现基本的表达式评估,现在让我们继续深入探讨解释器的最后一部分:用户界面,以及如何处理异常。这个解释器实现了一个交互式的 “读-评估-打印” 循环(REPL),并在其中处理各种可能的错误,确保用户能够连续地输入和评估表达式。
在一个编程语言的解释器中,REPL(Read-Eval-Print Loop)是用户与语言交互的核心机制。它使得用户可以输入表达式,解释器会读取这些输入、解析并计算它们的值,最后将结果打印出来。这是交互式编程的重要特性。
REPL 的流程如下:
- 读取(Read):提示用户输入一个表达式,并读取用户的输入。
- 解析(Parse):将输入的文本解析为表达式,通常是通过词法分析和语法分析生成抽象语法树。
- 评估(Eval):对解析后的表达式进行求值。
- 打印(Print):将评估结果输出给用户。
- 循环:回到第一步,继续等待新的输入。
REPL 的实现
在这个 Scheme 语法计算器中,REPL 的实现是通过一个 while 循环持续等待用户输入,直到用户输入结束信号(例如 Ctrl+D 或文件结束符)。错误处理是该循环的关键部分,它确保当输入或评估过程中出现错误时,解释器不会崩溃,而是能够显示错误信息并等待用户的下一个输入。
def repl():
"""Read-Eval-Print Loop"""
while True:
try:
# 提示用户输入
expression = input('calc> ')
# 解析表达式
parsed_expression = scheme_read(expression)
# 评估表达式
result = calc_eval(parsed_expression)
# 打印结果
print(result)
# 异常处理:捕获语法错误、类型错误、值错误和除零错误
except (SyntaxError, TypeError, ValueError, ZeroDivisionError) as e:
print(f"Error: {e}")
# 检测到文件结束符或用户中断退出
except EOFError:
print("Calculation is complete.")
break
异常处理
解释器中的异常处理非常重要,因为在用户输入、解析、评估表达式时,可能会发生各种错误。通过 try-except 机制,解释器可以捕获这些错误并打印出有用的错误信息,而不是崩溃或退出程序。这样用户可以修正输入,并继续使用解释器。
常见的异常类型:
-
SyntaxError:当输入的表达式不符合语言的语法时,解析阶段会抛出此异常。例如,输入不平衡的括号(1 + 2时会触发该异常。 -
TypeError:当不合法的运算符或操作数被使用时,会抛出此异常。例如,对一个字符串尝试进行加法操作会导致TypeError。 -
ValueError:例如,解析无效的数字格式(如2.3.4)时,可能会抛出ValueError。 -
ZeroDivisionError:当在计算过程中试图除以零时,Python 内置的除法运算会抛出此错误。
每个错误都有其独特的处理方式,确保在任何出错的情况下,解释器都能够处理并提示用户发生了什么问题。
calc_apply 函数的进一步实现
我们之前讨论了 calc_apply 函数如何处理各种运算符,并根据操作数进行计算。这里的运算符包括 +、-、* 和 /。如果传递给运算符的操作数不合法(例如,传入了无效的操作数数量),calc_apply 将抛出一个类型错误。具体代码如下:
def calc_apply(operator, arguments):
if not isinstance(operator, str):
raise TypeError(f"'{operator}' is not a valid operator")
if operator == '+':
return sum(arguments)
elif operator == '-':
if len(arguments) == 0:
raise TypeError("'-' requires at least one argument")
elif len(arguments) == 1:
return -arguments[0]
return arguments[0] - sum(arguments[1:])
elif operator == '*':
result = 1
for arg in arguments:
result *= arg
return result
elif operator == '/':
if len(arguments) == 0:
raise TypeError("'/' requires at least one argument")
elif len(arguments) == 1:
return 1 / arguments[0]
result = arguments[0]
for arg in arguments[1:]:
result /= arg
return result
else:
raise TypeError(f"Unknown operator: {operator}")
异常处理的整合
通过在 REPL 循环中捕获异常,解释器可以在发生错误时给予用户友好的反馈,并允许用户继续输入其他表达式。例如,如果用户输入了无效的运算符,解释器将输出错误信息而不是崩溃。具体实现如下:
def repl():
"""Read-Eval-Print Loop for the calculator."""
while True:
try:
expression = input("calc> ")
if not expression:
continue
parsed = scheme_read(expression)
result = calc_eval(parsed)
print(result)
except (SyntaxError, ValueError, TypeError, ZeroDivisionError) as err:
print(f"Error: {err}")
except EOFError: # Ctrl+D 终止输入
print("Calculation is complete.")
break
通过这些实现,用户可以安全、连续地在解释器中输入和评估表达式,体验到类似于命令行计算器的交互式编程体验。