Lecture 7. Function Examples

Announcements

期中考试一将于周一晚上7点举行。如果你需要调整考试时间，或申请免除监考政策，请务必在今天完成申请。考试期间，你需要使用Zoom、Loom或手机录制屏幕和头部，我们试图让这一过程尽量灵活、不那么繁琐。建议你提前练习录制一个2小时的视频，确保考试当天一切顺利运行。

Practice Exam

练习考试将在周五下午1点到2点和晚上7点到8点进行。如果你无法参加这两个时间段的练习考试，考试将在周五晚上8点至周日晚上8点的48小时内开放，可以自行安排时间。练习考试虽然比正式考试短，但强烈建议你参加，这样你可以熟悉考试的软件环境并进行适当的练习。

考试规则

你可以准备一张双面的笔记，但必须自己创建。
你可以使用草稿纸。
如果要存储笔记电子版，必须使用Google文档，并授予我们编辑权限以便查看文档内容。
学生组织HKN将在周六举办复习会，详情见Piazza帖子。

其他重要信息

本周五将有一次考试准备环节，这是每周五的惯例。
下周没有实验和作业，也没有周一的讲座。周三将有讨论和教程，但周一除了期中考试外，没有其它安排。
Hog项目的截止日期为本周五，如果今天提交，可以获得提前提交奖励分。项目第七题在上次讲座的问答环节中有所讨论，你可以点击链接查看相关内容。

Hog策略比赛

如果你想要在期中考试之后做点有趣的事，可以参加Hog策略比赛，这完全是可选的，只是为了好玩。你可以提交一个最终策略，然后我们会将所有策略相互对战，看看哪一个策略表现最好。

规则更新

在所有的额外回合中，你将使用八面骰子而非六面骰子，这降低了掷出1的几率并提高得分机会。
比赛允许两人组队，但每个人只能参加一组。
每个策略的胜负基于精确的概率计算，而非实际掷骰子模拟。
所有策略必须是确定性策略，即仅基于分数决定掷骰子的数量，而不考虑是否会有额外回合。
获胜者将获得少量的额外学分，第一名3分，第二名2分，第三名1分。

需要注意的是，参与策略比赛可能耗费大量时间，而获得的学分非常少，因此对最终成绩的影响微乎其微。

重要链接

考试和复习的相关Zoom链接、讲座问答、以及与考试准备相关的Google Drive目录已经提供，需使用伯克利账号登录查看内容。

比赛和考试准备的细节已经在Piazza上发布，建议尽早查看和准备。

参加这场比赛真正的奖励是荣誉与荣耀。每学期的Hog策略比赛获胜者的名字都会被记录下来，并且长期保存在课程的历史中，从2015年到现在。即使比赛规则可能会有所变化，但获胜者的名字将永远留在课程的讲义中，直到比赛被取消的那一天（如果那天会到来的话）。因此，无论策略简单或复杂，你都可以提交并参与其中。

Describing Functions

Decorators

在今天的课程中，虽然主要是复习内容，但也有一个新话题：装饰器（Decorators），这是Python中的一个高级功能。这个话题不会出现在期中考试中，但它是教材第1.6章中的一个有趣内容。装饰器允许你修改函数的行为而不改变函数的代码，我们会在课后提到这个概念。

复习建议

建议复习的方式如下：

在看到复习问题时，暂停视频，自己先思考解决方法。
然后再听讲师的讲解，了解如何分析和解答这些问题。

你可以选择参加考试准备和复习环节，这些对期中考试的准备非常有帮助。此外，可以回顾一到两份往年试卷，但没有必要过多研究。最重要的是保持放松，充足的休息能帮助你在考试中发挥出最佳水平。

期中考试的评分机制

即使你跳过考试中的最难题目，只要解决了其余部分，你仍然有机会获得A。
不必追求完美，只需尽力发挥即可。
如果在考试中遇到你暂时无法解决的问题，保持冷静，避免因焦虑导致整体表现下降。

期中考试题型示例

在期中考试中，你可能会遇到类似这样的题目：根据一个函数的实现描述其行为。

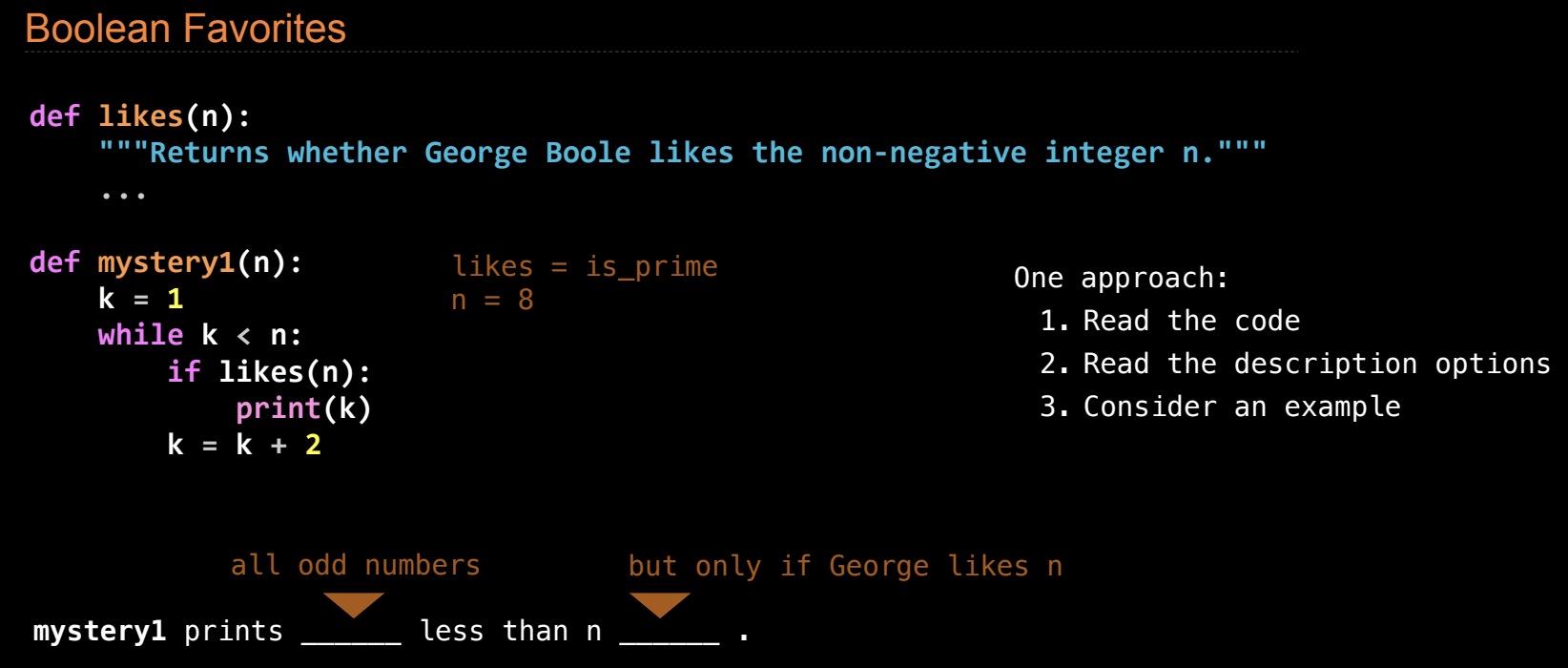
在这个例子中，我们定义了一个函数 mystery1，它根据某种规则，打印小于 n 的奇数。这段代码背后涉及的逻辑依赖于另一个函数 likes(n)，这个函数会决定 George Boole 是否喜欢某个非负整数 n。虽然 likes(n) 的实现细节未展示，但通过 mystery1 的循环结构，我们可以推测出代码的执行流程。

1. `mystery1(n)` 函数

def mystery1(n):
    k = 1
    while k < n:
        if likes(n):
            print(k)
        k = k + 2

这个函数的作用是遍历从 1 开始的小于 n 的所有奇数，并在满足特定条件时输出这些奇数。让我们逐行分析它的行为：

k = 1：初始化计数器 k，从 1 开始。
while k < n：进入 while 循环，只要 k 小于 n，继续执行循环体。
if likes(n)：在每次循环中，检查函数 likes(n) 的返回值。如果 likes(n) 返回 True，则打印当前的 k 值。
k = k + 2：每次循环后，k 增加 2，这意味着循环每次只检查奇数（k 依次为 1, 3, 5…）。

2. `likes(n)` 函数

def likes(n):
    """Returns whether George Boole likes the non-negative integer n."""
    ...

虽然 likes(n) 函数的实现细节没有给出，但它的作用是判断 George Boole 是否“喜欢”某个数 n。结合示例和代码提示，likes(n) 可能用于筛选特定的数值，比如判断是否是质数（is_prime），或者是否满足其他某些条件。

示例推测

假设 likes(n) 是一个用来判断某个数是否是质数的函数（如 is_prime），那么 mystery1(n) 的行为就是：

遍历小于 n 的所有奇数。
只打印那些满足 likes(n) 条件的奇数。

如果我们运行 mystery1(8)，假设 likes(8) 返回 False，则 mystery1 不会打印任何奇数。相反，如果 likes(8) 返回 True，那么它会打印所有小于 8 的奇数，即 1、3、5、7。

函数 mystery1(n) 的行为可以总结为：它会打印所有小于 n 的奇数，但前提是当前的 n 满足 likes(n) 的条件。通过这个函数，我们可以进一步推断出，likes(n) 的实现很可能涉及某种数值特征的判断，例如质数检测。

`mystery2` 函数

在这个例子中，mystery2(n) 函数通过查找小于 n 的整数，试图找出两个 George Boole 喜欢的整数之间的最小差值。如果没有找到两个符合条件的整数，它将返回 None。

1. 代码结构解析

def mystery2(n):
    i, j, k = 0, None, None  # 初始化变量 i, j, k
    while i < n:  # 当 i 小于 n 时，进入循环
        if likes(i):  # 如果 George 喜欢 i
            if j != None and (k == None or i - j < k):  # 如果 j 已被赋值，并且当前差值更小
                k = i - j  # 更新 k 为 i 和 j 之间的差值
            j = i  # 将 j 更新为当前的 i
        i = i + 1  # i 自增 1，继续下一个数字
    return k  # 返回最小差值

变量说明：

i：当前正在检查的数字，初始值为 0。
j：存储上一个 George 喜欢的数字，如果还没有找到这样的数字，则 j = None。
k：存储最小的两个 George 喜欢的数字之间的差值，初始值为 None，表示还没有找到符合条件的差值。

2. 核心逻辑解析

主循环 while i < n

mystery2(n) 函数从 0 开始遍历所有小于 n 的数字。在每一次循环中，它通过 likes(i) 来检查 George Boole 是否喜欢当前数字 i。如果 likes(i) 返回 True，即 George 喜欢这个数字，则进入下一步判断：

第一次找到喜欢的数字：如果 j 还没有被赋值（即 j == None），这意味着这是我们第一次找到 George 喜欢的数字，此时只需将 j 更新为当前的 i。
第二次及以后找到喜欢的数字：如果 j 已经被赋值，且 k 还没有被初始化或者当前差值 i - j 小于 k，那么我们就更新 k 为 i - j，即 George 喜欢的两个数字之间的最小差值。

循环结束

循环结束后，函数返回找到的最小差值 k。如果在整个过程中只找到一个或者没有找到 George 喜欢的数字，k 依然保持 None，函数将返回 None。

3. 示例运行

让我们通过一些例子来理解函数的行为。

示例 1：mystery2(10)，假设 likes(i) 返回的结果如下：

likes(0) -> False
likes(1) -> True
likes(2) -> False
likes(3) -> True
likes(4) -> False
likes(5) -> False
likes(6) -> True

执行步骤：

i = 0：likes(0) 返回 False，跳过。
i = 1：likes(1) 返回 True，j 被赋值为 1。
i = 2：likes(2) 返回 False，跳过。
i = 3：likes(3) 返回 True，此时 i - j = 3 - 1 = 2，更新 k = 2，j 被更新为 3。
i = 4, 5：likes(4), likes(5) 返回 False，跳过。
i = 6：likes(6) 返回 True，此时 i - j = 6 - 3 = 3，因为 3 大于当前的 k = 2，不更新 k，j 被更新为 6。

最终返回值为 k = 2，表示 George 喜欢的两个数 1 和 3 之间的最小差值是 2。

示例 2：mystery2(5)，假设 likes(i) 只有一个 True 值：

likes(0) -> False
likes(1) -> True
likes(2) -> False
likes(3) -> False
likes(4) -> False

执行步骤：

i = 0, 2, 3, 4：likes(i) 返回 False，跳过。
i = 1：likes(1) 返回 True，j 被赋值为 1。

因为整个过程中只找到了一个 George 喜欢的数字，k 一直为 None。函数将返回 None。

总结

mystery2(n) 函数的作用：它返回 George Boole 喜欢的两个整数之间的最小差值，如果找不到两个这样的整数，则返回 None。
执行流程：
1. 遍历从 0 到 n-1 的所有整数。
2. 如果 George 喜欢某个整数，则检查与之前找到的喜欢的整数之间的差值，记录最小差值。
3. 返回最小差值或 None，表示没有找到两个符合条件的数字。

通过这个例子，我们可以看到如何使用逻辑控制结构（while、if 语句）来解决搜索问题，尤其是当条件判断（如 likes 函数）决定程序的执行路径时，灵活的条件判断可以帮助我们有效找到目标值。

解题策略

逐行理解代码：不要仅凭直觉解答问题。仔细阅读每一行代码，分析每个变量的变化。
假设特定条件：通过假设 likes 函数的行为，手动推导代码的执行流程。
验证多个示例：通过不同的输入条件验证代码的行为，确保理解无误。
记住边界条件：例如，当没有 k 值被赋值时，函数应返回 None。

环境图题目

另一类可能遇到的题目是根据环境图推导代码。对于这类问题：

理解环境图：首先仔细观察环境图，了解函数的调用顺序、变量的绑定和返回值。
推断代码逻辑：通过环境图中记录的函数调用和返回值，推断出每一步的代码。
关注细节：注意每个变量在环境中的变化，尤其是递归调用或 lambda 函数的情况。

在环境图问题中，要求我们根据给定的环境图推断出生成该图的代码。这类问题与直接分析代码生成环境图相反，需要具备对变量绑定、函数调用以及控制流的深刻理解。下面我们结合一个复杂的“flip-flop”函数示例，演示如何从环境图推导出代码。

分析环境图与代码推导

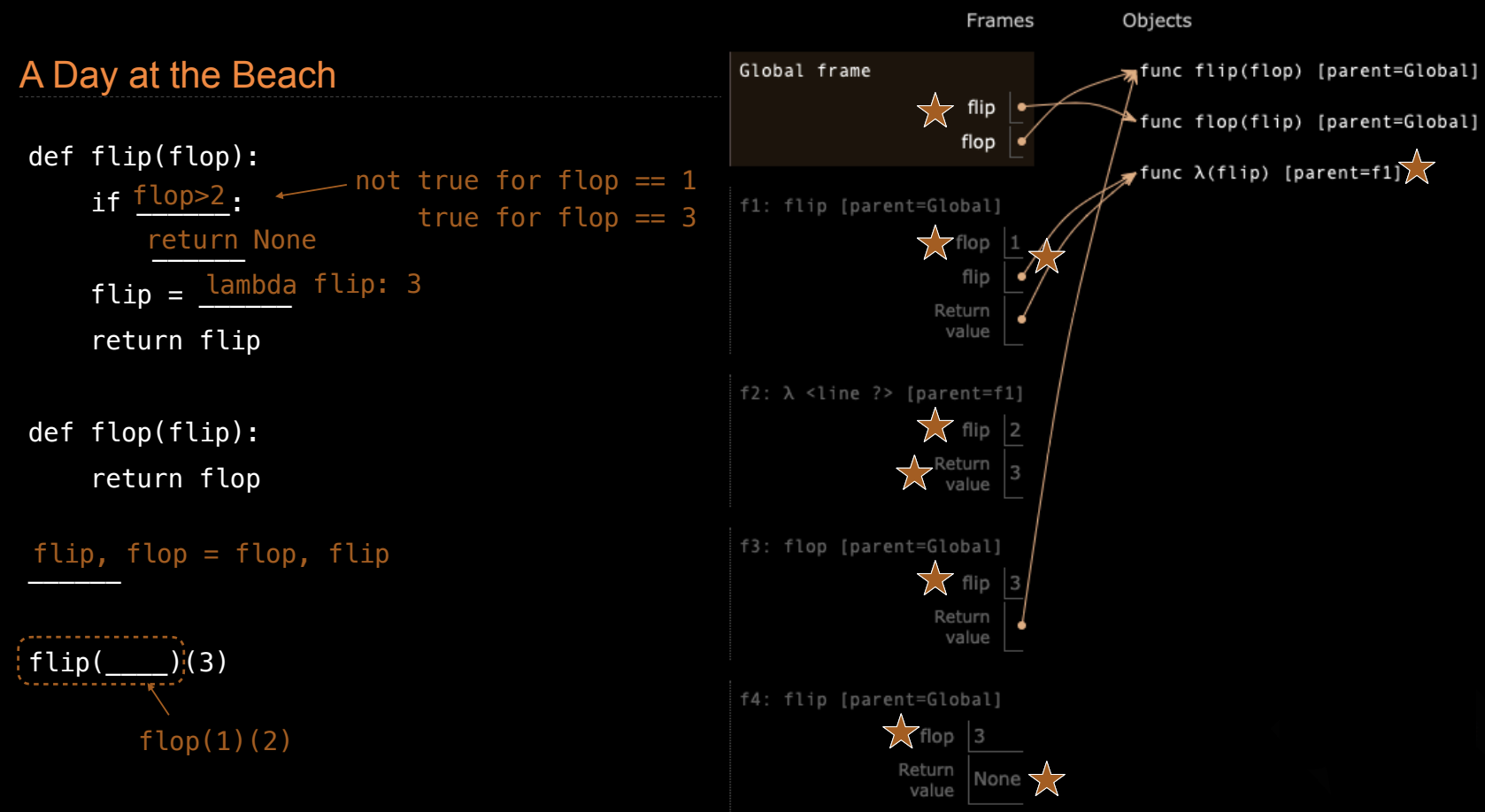
QQ_1726017219831

根据环境图，我们需要推导出 flip 和 flop 函数的行为。以下是对每一帧的逐步分析，帮助我们理解代码是如何构造的。

1. 全局帧（Global frame）

定义了 flip 和 flop 函数：在全局帧中，flip 和 flop 函数最初是各自绑定的。
变量交换：环境图中显示，在某一时刻，flip 和 flop 的名称发生了互换。这表明代码中必须包含多重赋值语句，比如：
```
flip, flop = flop, flip
```

2. 帧 `f1`：`flip(1)` 被调用 [由`flop(1)`]

调用 flip(1)：在这个帧中，flip 函数接收参数 flop = 1，进入 flip(1) 的执行。
函数 flip(1) 返回了一个匿名函数 lambda。
- flip 函数没有直接返回值，而是返回了一个匿名函数。
- 匿名函数 lambda 的名字和参数为 flip
此时，flop 作为全局函数的名字，实际上指向了 flip 的实现（因交换后，flip 和 flop 被互换了）。

这部分flip(1) 被调用 [由flop(1)] 返回了一个匿名函数 lambda

3. 帧 `f2`：`lambda` 函数被调用 [由`flop(1)(2)`]

调用 lambda flip: 3：返回的匿名函数在帧 f2 中被调用，传入参数 flip = 2，并返回 3。可以猜测 lambda 函数始终返回 3，无论传入什么参数。
```
flip = lambda flip: 3
```
这部分 lambda 函数被调用 [由flop(1)(2)] 返回 3

4. 帧 `f3`：`flop(3)` 被调用 [由`flip(flop(1)(2))`]

调用 flop(3)：在这个帧中，flop 函数接收参数 flip = 3。此时 flop 返回了 flip 函数的实现。由于 flip 和 flop 在全局中已经互换，flop() 返回 flip 函数的实现，实际上返回名字flop。
flop 函数的逻辑可以为直接返回flop ：
```
def flop(flip):
    return flop
```

这部分flop(3) 被调用 [由flip(flop(1)(2))] 返回 flop [实际上是flip()]

5. 帧 `f4`：`flip(3)` 被调用 [由`flip(flop(1)(2))(3)`]

调用 flip(3)：flip(3) 接收参数 flop = 3，可以假设，如果 flop > 2，函数返回 None。因此，flip(3) 返回 None。
这说明 flip 函数中的条件判断逻辑是：
```
if flop > 2:
    return None
```

整合推导出的代码

基于以上分析，完整的代码应如下：

def flip(flop):
    if flop > 2:
        return None
    flip = lambda flip: 3  # 返回 lambda 函数，无论输入什么，都返回 3
    return flip

def flop(flip):
    return flop  # 返回它的参数

# 交换 flip 和 flop 的绑定
flip, flop = flop, flip

# 调用 flip(flop(1)(2))(3)
result = flip(flop(1)(2))(3)
print(result)  # 输出应为 None

代码执行流程

调用 flop(1)：
- flop(1) 返回 1。此时 flop 被绑定到原先的 flip 函数。
调用 flop(1)(2)：
- flop(1) 返回 1。此时 flop 被绑定到原先的 flip 函数。
- 此时 flip 返回匿名函数 lambda flip: 3。
- 然后，lambda 函数被调用，传入参数 2，并返回 3。
调用 flip(3) [或者说 flip(flop(1)(2))]：

flip(3) 进入 flop 函数，参数flip = 3，返回 flop[指向flip(flop)]。
调用 flop(3)：
- flop(3) 进入 flip 函数，参数flop = 3，根据条件判断，3 > 2，因此返回 None。

Implementing Functions

编写函数的策略

在 CS61A 期中考试中，另一类常见问题是要求你编写一个特定功能的函数。以下是一些通用的策略，适用于在纸上或计算机上实现函数。

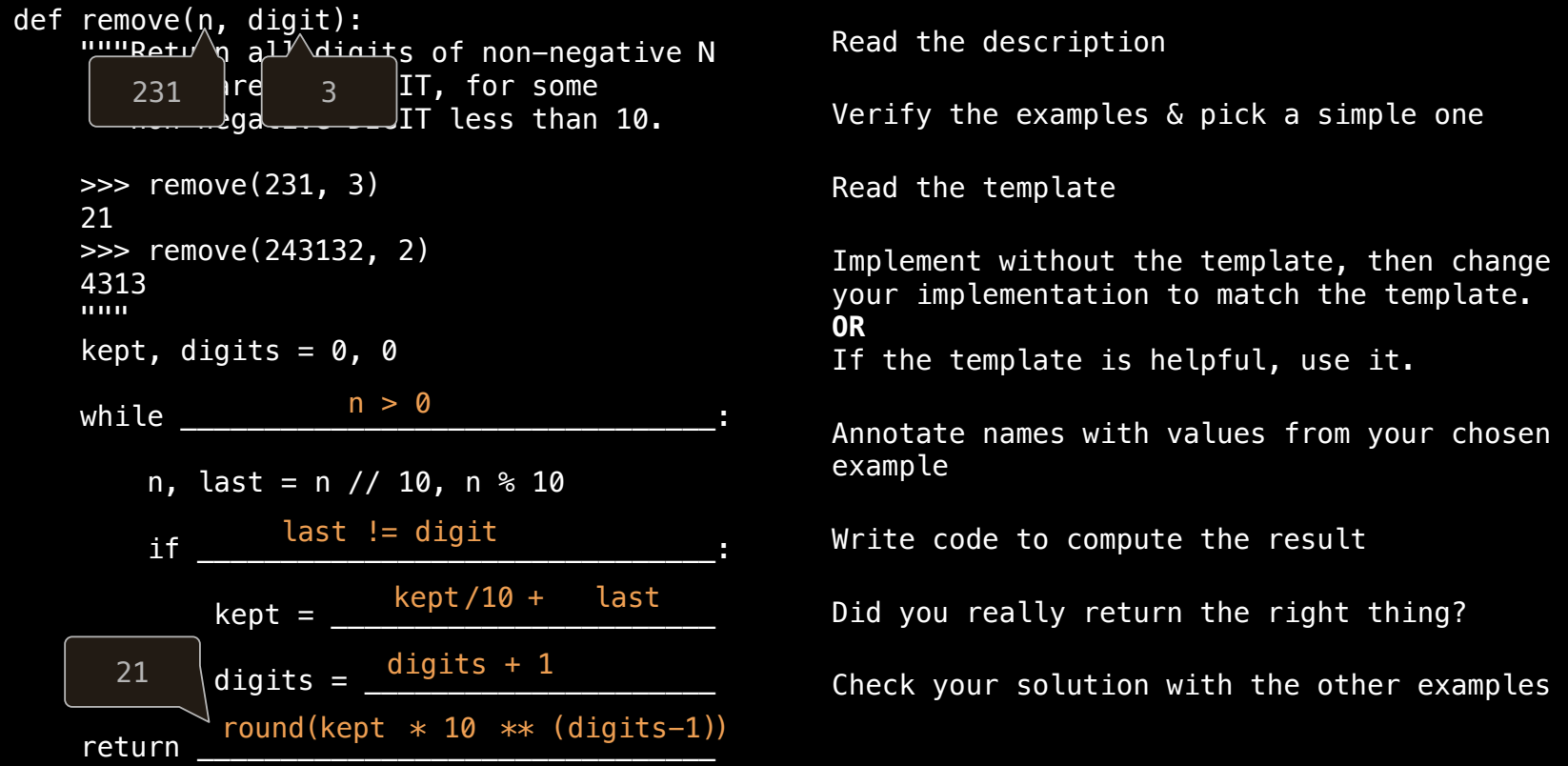
示例题：移除数字

问题要求你实现一个函数 remove(n, digit)，它返回去掉数字 n 中所有等于 digit 的数字后的新整数。以下是解题步骤：

理解问题：函数需要遍历整数 n 的每一位，去掉与 digit 相同的数字，然后返回一个新的整数。
分解问题：将 n 分解成一系列数字，并逐个检查每个数字是否与 digit 相同。
重建整数：将保留下来的数字重新组合成一个新的整数。

初步思路

目标：函数 remove(n, digit) 接收一个非负整数 n 和一个要移除的数字 digit，返回一个整数，表示 n 中所有非 digit 的数字。
示例：

remove(2313, 3) 应返回 21。
remove(24313, 4) 应返回 2313。

解题策略

逐位遍历 n：我们需要逐位处理 n 的每个数字，判断该数字是否等于 digit。如果不等，则保留该数字。
构建新整数：为了保持数字的顺序，保留的数字需要按正确的位数重建。例如，如果保留 2 和 1，我们应该返回 21 而不是 3（2 + 1）。

模板与代码结构

模板中已经提示了我们将会初始化两个变量：kept 和 digits。kept 用于存储移除 digit 后剩余的数字，而 digits 用来跟踪位数，以确保我们能按正确的顺序构建新整数。

实现步骤

初始化变量：
- kept = 0：用于存储最终结果。
- digits = 1：用于跟踪当前正在处理的位数。
逐位处理 n：
- 使用 while 循环遍历 n 的每一位数字。
- 每次提取 n 的最后一位数字，判断它是否与 digit 相同。如果不同，则将该数字添加到 kept 中。
- 将处理过的最后一位从 n 中移除。
正确重建整数：
- 使用 digits 变量跟踪位数。每次添加新的数字时，将 kept 乘以 10 以确保数字按正确的顺序排列。

代码实现

def remove(n, digit):
    kept = 0
    digits = 1
    while n > 0:
        last = n % 10  # 提取最后一位数字
        if last != digit:  # 如果不等于要移除的 digit
            kept = kept + last * digits  # 将该数字加入结果
            digits *= 10  # 更新位数
        n //= 10  # 去掉最后一位
    return kept

逐步验证

示例 1：remove(2313, 3)

初始化：kept = 0，digits = 1
第一次迭代：
- last = 3，跳过。
- n = 231
第二次迭代：
- last = 1，kept = 0 + 1 * 1 = 1，更新 digits = 10。
- n = 23
第三次迭代：
- last = 3，跳过。
- n = 2
第四次迭代：
- last = 2，kept = 1 + 2 * 10 = 21。
- n = 0，结束循环。

结果：remove(2313, 3) 返回 21。

调整与优化

位数跟踪：通过 digits 跟踪保留数字的位数，确保数字按正确的顺序组合。
跳过 digit：只有当提取的数字不等于 digit 时，才将其加入到结果中。

复杂度分析

时间复杂度：每次迭代处理 n 的一位数字，因此时间复杂度为 O(d)，其中 d 是 n 的位数。
空间复杂度：使用常数空间存储 kept 和 digits，因此空间复杂度为 O(1)。

这个实现的核心是逐位遍历 n，根据条件保留或丢弃某些数字，并通过跟踪位数确保结果的正确性。通过逐步验证和调试，确保代码能够正确处理不同的输入和边界情况。

函数装饰器（Function Decorators）

在 Python 中，函数装饰器是一种简洁且强大的语法，用于修改或扩展函数的行为。装饰器本质上是一个接受函数作为参数的函数，并返回一个新的函数（或者返回经过修改的原函数）。装饰器常用于在不改变函数内部代码的情况下增强函数的功能，例如添加日志记录、性能计时、权限验证等功能。

装饰器的工作原理

以下两种代码方式是等效的：

1. 使用装饰器语法的方式

@trace1
def triple(x):
    return 3 * x

这里的 @trace1 是一个装饰器，直接放在 triple 函数的定义上方。它的作用是将 triple 函数传递给装饰器 trace1 进行处理，trace1 可以修改或增强 triple 的行为，并返回一个新的函数，最后该新的函数替代原来的 triple。

2. 等效的传统方式

def triple(x):
    return 3 * x

triple = trace1(triple)

这段代码手动将 triple 函数传递给装饰器 trace1，并将 trace1 的返回值重新赋给 triple。这样，triple 函数实际上已经被 trace1 装饰器处理过，之后对 triple 的调用会执行装饰器中的逻辑。

两种方式等效

这两种写法是等效的。第一种方法使用了装饰器语法糖（syntactic sugar），更简洁直观。而第二种方式则是显式地调用装饰器函数，将其应用于目标函数。

为什么使用装饰器？

装饰器语法（@decorator）提供了许多优点：

代码更简洁：装饰器可以在函数声明时直接应用，避免在每次函数定义后手动调用装饰器函数。
功能增强：装饰器可以在不修改原函数的情况下，轻松添加新功能，比如记录函数调用日志、计算执行时间、权限验证等。
可复用：装饰器可以非常灵活地复用于多个函数，不必每次重复编写相同的增强逻辑。

装饰器的实际应用

一个简单的装饰器示例可能是记录函数的调用过程：

def trace1(func):
    def wrapper(*args, **kwargs):
        print(f"Calling {func.__name__} with {args} and {kwargs}")
        result = func(*args, **kwargs)
        print(f"{func.__name__} returned {result}")
        return result
    return wrapper

@trace1
def triple(x):
    return 3 * x

# 调用 triple(5)
triple(5)

输出结果：

Calling triple with (5,) and {}
triple returned 15

在这个例子中，trace1 装饰器将 triple 函数包裹在 wrapper 函数中。每次调用 triple(5) 时，装饰器会首先打印调用信息，然后调用原始的 triple 函数，最后打印返回值。

总结

装饰器语法（@decorator）使得代码更加简洁和直观。
通过使用装饰器，开发者可以轻松地为函数添加额外的功能，而无需更改函数的内部实现。
装饰器广泛用于日志记录、权限管理、性能监控等场景。

Lecture 7. Function Examples

Announcements

Practice Exam

考试规则

其他重要信息

Hog策略比赛

重要链接

Describing Functions

Decorators

复习建议

期中考试的评分机制

期中考试题型示例

1. mystery1(n) 函数

2. likes(n) 函数

示例推测

mystery2 函数

1. 代码结构解析

2. 核心逻辑解析

3. 示例运行

总结

解题策略

环境图题目

分析环境图与代码推导

1. 全局帧（Global frame）

2. 帧 f1：flip(1) 被调用 [由flop(1)]

3. 帧 f2：lambda 函数被调用 [由flop(1)(2)]

4. 帧 f3：flop(3) 被调用 [由flip(flop(1)(2))]

5. 帧 f4：flip(3) 被调用 [由flip(flop(1)(2))(3)]

整合推导出的代码

代码执行流程

Implementing Functions

编写函数的策略

示例题：移除数字

初步思路

解题策略

模板与代码结构

实现步骤

代码实现

逐步验证

调整与优化

复杂度分析

函数装饰器（Function Decorators）

装饰器的工作原理

1. 使用装饰器语法的方式

2. 等效的传统方式

两种方式等效

为什么使用装饰器？

装饰器的实际应用

总结

1. `mystery1(n)` 函数

2. `likes(n)` 函数

`mystery2` 函数

2. 帧 `f1`：`flip(1)` 被调用 [由`flop(1)`]

3. 帧 `f2`：`lambda` 函数被调用 [由`flop(1)(2)`]

4. 帧 `f3`：`flop(3)` 被调用 [由`flip(flop(1)(2))`]

5. 帧 `f4`：`flip(3)` 被调用 [由`flip(flop(1)(2))(3)`]