Lecture 10. Containers

Announcements

  1. 期中考试重评分申请截止时间：期中考试1的重评分申请截止于周一。请确保你上传的期中考试录音链接在周一前仍然有效。如果需要更长时间保存，你将会收到通知。否则，你可以在周二之后删除它们，以释放Google Drive空间。

  2. 作业与实验：
    • 作业2：作业2的截止时间是周四。请按时提交作业。
    • 实验：本周有实验安排，实验在周二截止。建议大家在周一完成实验，如果有任何问题，可以参加周一的实验指导。
  3. 完全可选的Hog策略竞赛：
    • Hog策略竞赛将在周一结束。到目前为止，已经有112个提交。虽然目前有四名选手并列第一名，但往往会有同学在最后一刻提交最优的策略。
    • 欢迎大家继续参加，尽早提交可以查看你在竞赛排行榜中的排名情况。
  4. 本周其他安排：
    • 讨论课和辅导课：将在周三进行。
    • 考试准备环节：安排在周五，这将帮助大家复习并准备未来的考试。
    • 问答环节：将在周一、周三和周五的早上进行，通过Zoom与授课教师进行交流。

本次课程内容概述

今天的课程将介绍如何给多个值命名，并使用容器将它们打包在一起。此外，还会讲解字符串的相关内容，因为它们本质上是包含字母的容器。

列表（Lists）

image-20240912104418507

什么是列表？

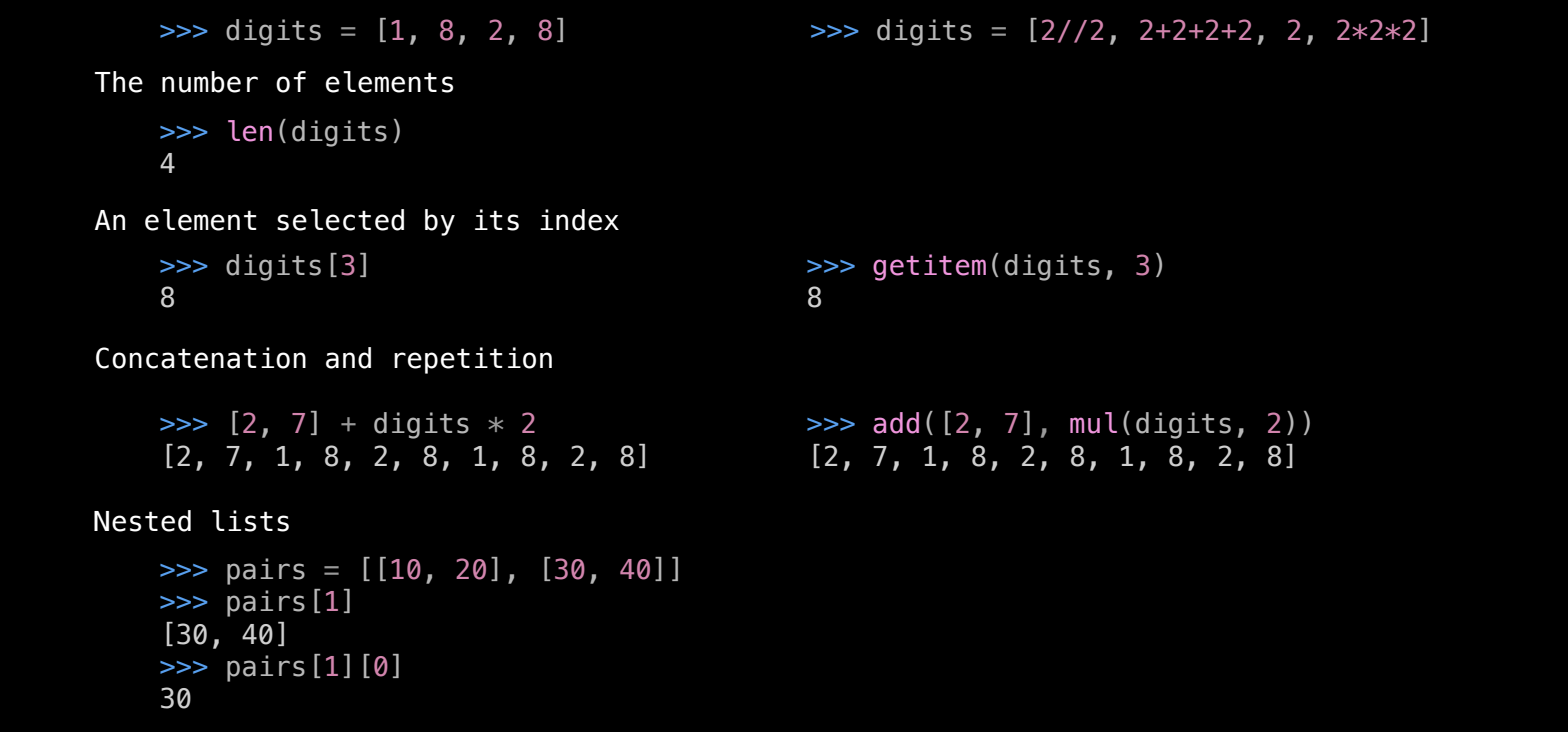
列表是 Python 中的内置数据类型之一，专门用于存储一系列的值。这些值可以通过列表字面量（list literals）创建，并通过赋值语句将其绑定到变量名。列表中的元素可以通过索引进行访问，索引从 0 开始。

  • 示例： 
    odds = [1, 3, 5, 7]  # 创建一个包含奇数的列表
print(odds[0])  # 输出列表的第一个元素，结果为 1

获取列表的长度

可以使用内置的 len() 函数来获取列表的长度。该函数返回列表中元素的个数。

  • 示例： 
    len(odds)  # 返回 4，表示列表有四个元素

列表操作

列表在 Python 中支持各种操作，例如相加和重复。

  • 列表相加：使用 + 运算符将两个列表合并。 
    [1, 2] + [3, 4]  # 返回 [1, 2, 3, 4]
  • 列表重复：使用 * 运算符重复列表中的元素。 
    [1, 2] * 2  # 返回 [1, 2, 1, 2]

列表的元素类型

列表的元素可以是任何数据类型，甚至是另一个列表。因此，列表可以用来创建更复杂的嵌套结构。

  • 示例： 
    pairs = [[10, 20], [30, 40]]  # 嵌套列表
print(pairs[1])  # 返回 [30, 40]

Containers

in 操作符的用法

in 操作符用于检查某个元素是否存在于列表中，但只能检查单个元素，而不能检查子序列。

image-20240912104343515

  • 示例： 
    digits = [1, 8, 2, 8]
print(1 in digits)  # True，1 存在于列表中
print('1' in digits)  # False，字符串 '1' 与整数 1 是不同的类型
print([1, 8] in digits)  # False，不能检查子序列
  • 当列表中的元素本身是列表时，in 操作符可以检查列表是否包含另一个列表作为元素。 
    pairs = [[1, 2], [3, 4]]
print([1, 2] in pairs)  # True，列表 [1, 2] 是 `pairs` 的一个元素

in 操作符与for 循环

for 循环是遍历序列的常用方法，简化了手动管理索引的过程。与 while 循环不同，for 循环可以自动遍历序列中的每个元素，减少了出错的几率。

  • 示例：计算元素出现的次数： 
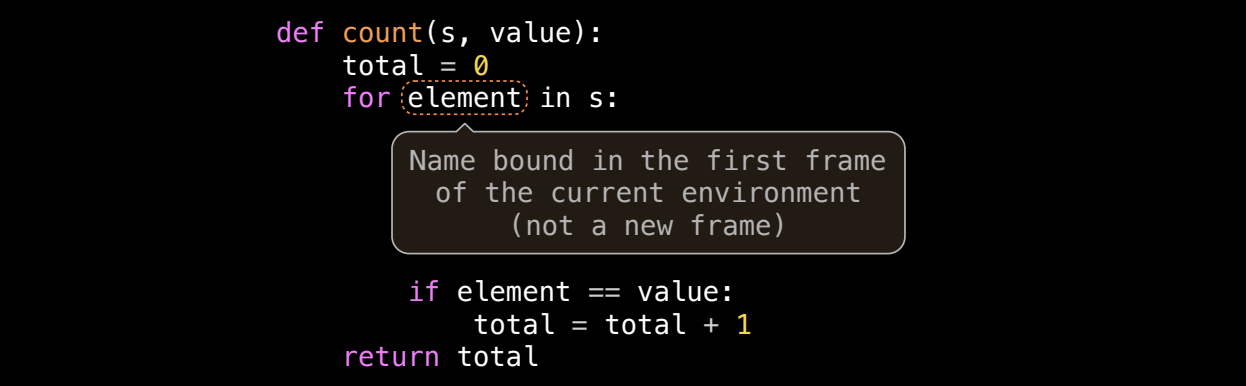
    def count(s, value):
    total = 0
    for element in s:
        if element == value:
            total += 1
    return total

在这个例子中，for 循环遍历列表 s，如果某个元素等于 value，则计数器 total 增加。这个方式消除了使用 while 循环时，手动维护索引的复杂性。

Python中的语法糖

Python 提供了许多简化操作的语法糖，这些简写使得代码更加简洁。例如，+= 操作符是一种常见的语法糖，等效于 total = total + 1。类似的操作符还包括 -=、*=、/= 等，这些操作符都可以帮助减少冗长的代码。

  • 示例： 
    total = 0
total += 1  # 等效于 total = total + 1

这种简化操作符在循环或累加操作中非常常见，能够显著简化代码的编写。

For Statements

image-20240912104507806

for 语句的语法解析

for 语句在 Python 中的基本语法如下：

for <name> in <expression>:
    <suite>
  • <expression> 是一个可迭代对象，例如列表、元组或字符串。
  • <name> 是每次循环时从 <expression> 中提取的元素，在循环体 <suite> 中进行处理。

每次循环时，Python 会从 <expression> 中提取一个元素赋值给 <name>，并执行 <suite> 中的代码，直到所有元素都遍历完毕。

  • 示例：遍历字符串 
    for char in "hello":
    print(char)

在这个例子中，for 循环遍历字符串中的每个字符，并逐一打印。

序列解包

for 语句的一个强大功能是序列解包。当列表或元组包含多个元素时，可以在 for 循环中自动解包这些元素并赋值给多个变量。这样做可以让代码更加简洁直观，特别是在处理嵌套结构时非常有用。

image-20240912104531986

  • 示例：解包元组中的元素

    pairs = [(1, 2), (3, 4), (5, 5)]
for x, y in pairs:
    if x == y:
        print(f"Pair ({x}, {y}) has identical elements.")

在这个例子中，x 和 y 分别从 pairs 列表中的每个元组中提取，并用于后续的条件判断和打印操作。序列解包的便利在于可以直接对复杂的嵌套结构进行处理，而无需显式地访问子元素。

嵌套列表的序列解包

对于嵌套列表结构，for 循环结合序列解包可以极大简化处理多个层次结构的代码。例如，处理一个包含多个子列表的列表，可以通过解包直接获取子列表中的各个元素。

  • 示例：解包嵌套列表中的元素 
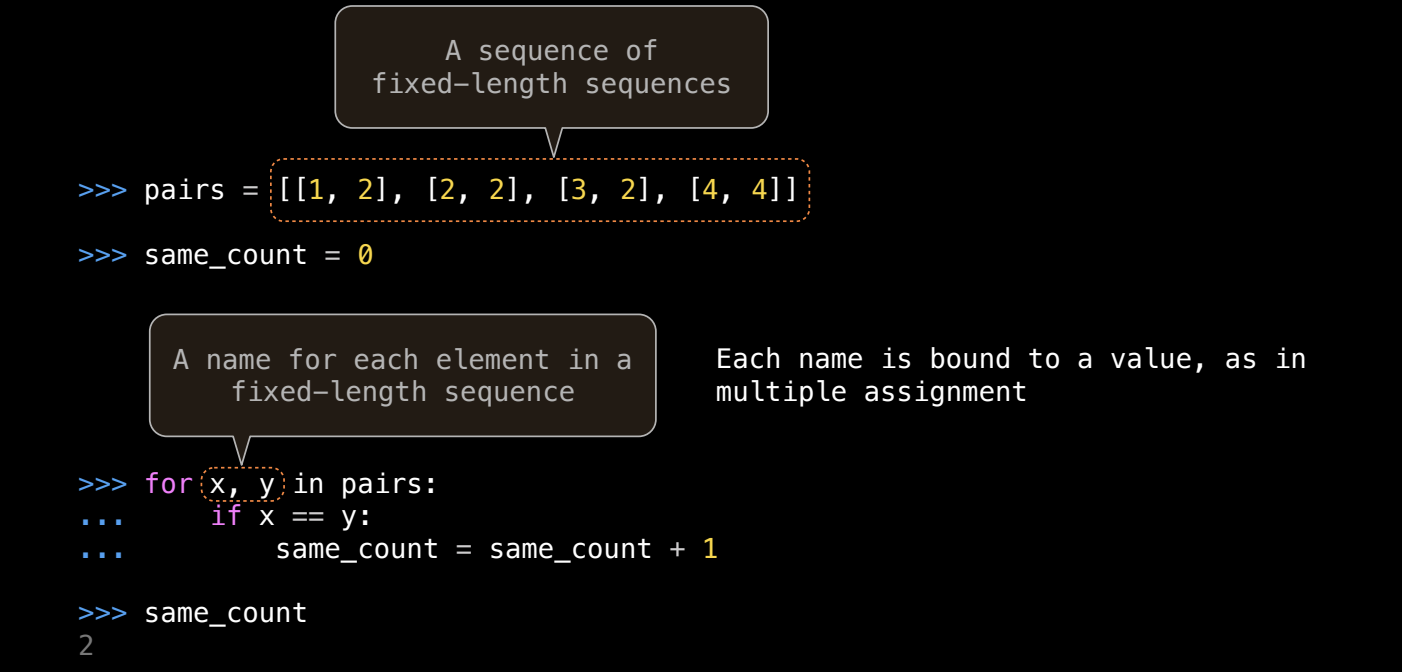
    pairs = [[1, 2], [2, 2], [3, 4]]
for x, y in pairs:
    if x == y:
        print(f"Pair ({x}, {y}) has identical elements.")

在这个例子中，for 循环直接解包每个子列表中的两个元素 x 和 y，并进行相等性检查。这种方式避免了手动访问子列表的元素，代码更为简洁和可读。

Ranges

range() 对象概述

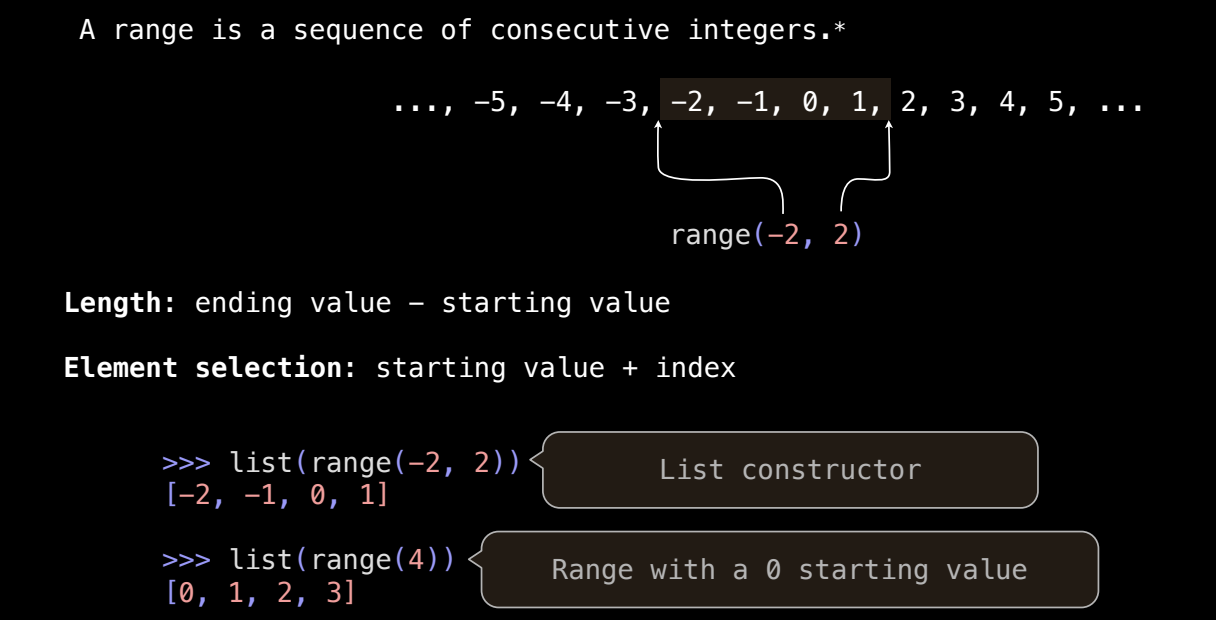
range() 是 Python 中一个非常常用的序列类型，通常用于生成一系列连续的数字。与传统的列表不同，range() 不会立即创建整个列表，而是以惰性方式生成数字序列，这使得它在处理大范围数字时更加高效。

image-20240912104613665

  • 重要特性：
    • range(start, end)：生成从 start 到 end（不包括 end）的数字序列。
    • 如果只提供一个参数，则表示从 0 开始，到指定的结束位置。例如，range(4) 会生成 0 到 3 的数字序列。
    • range() 是惰性生成的，也就是说，它不会立即生成所有数字，而是在需要时逐步产生。如果需要查看生成的所有数字，可以使用 list() 将其转换为列表。
  • 示例： 
    r = range(5, 8)  # 生成从 5 到 7 的数字序列，但尚未实际生成
print(list(r))   # 输出 [5, 6, 7]

这种惰性加载的机制使得 range() 在处理大范围数字时，既节省了内存，又能够高效完成任务。

在 for 循环中使用 range()

range() 经常用于 for 循环中，尤其是在需要固定次数的迭代时，它是最简单直接的选择。通过 range()，我们可以非常方便地生成一个指定范围内的数字，并在循环中进行迭代。

  • 示例：计算小于某个数字的所有整数之和： 
    def sum_below(n):
    total = 0
    for i in range(n):
        total += i
    return total
  
print(sum_below(5))  # 输出 10（0 + 1 + 2 + 3 + 4）

在这个例子中，range(n) 生成从 0 到 n-1 的数字，并通过 for 循环依次迭代这些数字，将它们相加。这样，程序能够方便地计算小于 n 的所有整数之和。

使用 _ 作为占位符

在某些情况下，我们需要重复执行某个操作多次，但对循环变量本身不感兴趣。为了强调这个变量是多余的，Python 社区通常会使用下划线 _ 作为变量名。这是一个非常常见的惯例，表示我们不会使用这个变量。

  • 示例：重复打印消息： 
    for _ in range(3):
    print("Go Bears!")
  • 输出： 
    Go Bears!
Go Bears!
Go Bears!

在这里，循环执行了三次，使用 _ 表明我们并不关心循环中的当前迭代值。

讲解：求和的迭代与递归实现

题目要求：

  1. 迭代求和：编写一个迭代函数，输入一个正整数 n，返回前 n 个整数的和。例如，sum(5) 应该返回 1 + 2 + 3 + 4 + 5 = 15。
  2. 递归求和：编写一个递归函数，完成相同的任务：求前 n 个整数的和。

第一部分：迭代解法

方法概述

迭代求和的基本思路是使用循环遍历从 1 到 n 的所有整数，并依次将它们累加到一个变量中。我们可以通过 for 循环来遍历这些数字，并将结果存储在一个累加器中，最终返回累加结果。

代码实现：

def iterative_sum(n):
    total = 0
    for i in range(1, n + 1):
        total += i
    return total

代码详解：

  1. 初始化：首先，定义一个变量 total，初始值为 0，它将用于累加从 1 到 n 的整数。
  2. 循环累加：通过 for 循环遍历从 1 到 n 的整数，并在每次迭代中将当前数字 i 加到 total 中。
  3. 返回结果：当循环结束时，total 中保存的就是前 n 个整数的和。

测试用例：

print(iterative_sum(5))  # 输出: 15

输出结果解释：

  • iterative_sum(5) 的执行结果为 15，因为它计算的是 1 + 2 + 3 + 4 + 5 的总和。

第二部分：递归解法

方法概述

递归是一种将问题分解为更小的子问题的技术。在求和问题中，递归思路是：sum(n) 可以表示为 n + sum(n-1)，即每次递归时减少一个数字，直到 n 等于 0（基准情况）为止。递归的关键在于确定基准情况和递归关系。

代码实现：

def recursive_sum(n):
    if n == 0:  # 基准情况
        return 0
    else:
        return n + recursive_sum(n - 1)  # 递归调用

代码详解：

  1. 基准情况：当 n 等于 0 时，直接返回 0。这是递归的终止条件。
  2. 递归调用：对于 n > 0 的情况，将 n 加上 sum(n-1)，通过递归继续调用该函数，逐步将问题缩小。
  3. 返回结果：当递归到达 n == 0 时，开始逐层返回结果，最终得出总和。

测试用例：

print(recursive_sum(5))  # 输出: 15

输出结果解释：

  • recursive_sum(5) 通过递归计算出 5 + 4 + 3 + 2 + 1 + 0 的总和，结果为 15。

递归过程详解

为了更好地理解递归的执行过程，我们可以通过一个示例 recursive_sum(5) 来跟踪函数的调用：

  1. 第一次调用：recursive_sum(5)，结果为 5 + recursive_sum(4)。
  2. 第二次调用：recursive_sum(4)，结果为 4 + recursive_sum(3)。
  3. 第三次调用：recursive_sum(3)，结果为 3 + recursive_sum(2)。
  4. 第四次调用：recursive_sum(2)，结果为 2 + recursive_sum(1)。
  5. 第五次调用：recursive_sum(1)，结果为 1 + recursive_sum(0)。
  6. 基准情况：recursive_sum(0)，结果为 0，递归终止。

函数开始返回时，依次将结果逐层返回：

  • recursive_sum(1) 返回 1 + 0 = 1。
  • recursive_sum(2) 返回 2 + 1 = 3。
  • recursive_sum(3) 返回 3 + 3 = 6。
  • recursive_sum(4) 返回 4 + 6 = 10。
  • recursive_sum(5) 返回 5 + 10 = 15。

最终，recursive_sum(5) 的结果是 15。

迭代与递归的比较

  1. 迭代：
    • 优点：简单易理解，通常在小规模任务中表现良好。空间复杂度较低，因为只使用一个累加器。
    • 缺点：对于更复杂的结构或问题，可能需要更多手动管理循环的逻辑。
  2. 递归：
    • 优点：递归能够自然地处理许多问题，尤其是那些可以分解为子问题的情况。代码往往更简洁，符合数学定义。
    • 缺点：对于大规模递归调用，可能会导致栈溢出（递归深度限制），并且每次递归调用都需要额外的栈空间。

在这道求和的题目中，迭代和递归都能有效解决问题。通过迭代，我们显式地使用循环结构求和；而通过递归，我们可以用分治的思路，将问题逐步简化。两种方法各有优劣，在实际编程中应根据具体情况选择合适的方式。

列表推导式 (List Comprehensions)

列表推导式提供了一种非常直观的方式来创建新的列表，它将一个循环、条件、以及对每个元素的处理整合成一个简短的表达式。其语法为：

image-20240912104814970

[expression for element in iterable if condition]
  • expression：定义你希望应用于每个元素的操作。它可以是对元素的直接引用、操作或函数调用。
  • element：表示当前正在迭代的元素。
  • iterable：表示你要遍历的序列（如列表、字符串或 range() 对象）。
  • if condition：可选部分，定义一个条件，仅包含满足条件的元素。

image-20240912104753797

示例 1：筛选和变换列表

假设我们希望找出 1 到 25 中所有能整除 25 的数，并返回这些数加 1 的结果：

[x + 1 for x in range(1, 26) if 25 % x == 0]
  • range(1, 26) 生成了从 1 到 25 的数字序列。
  • if 25 % x == 0 过滤出所有能整除 25 的数。
  • x + 1 将每个符合条件的数加 1。

结果为 [2, 6, 26]，因为 1、5 和 25 能整除 25，分别加 1 后得到 2、6 和 26。

示例 2：从字符串生成列表

我们可以使用列表推导式从字符串中提取每个字符，并且可以加上一些条件。

vowels = [char for char in "hello world" if char in 'aeiou']
  • char in "hello world" 提取字符串中的每个字符。
  • if char in 'aeiou' 过滤出所有元音字符。

结果为 ['e', 'o', 'o']。

函数中的列表推导式

列表推导式不仅可以直接在表达式中使用，也可以在函数内部使用，来生成和返回新列表。例如，如果我们需要找出一个数的所有因数，可以将列表推导式放在函数中实现。

示例：求某个数的所有因数 

def divisors(n):
    return [x for x in range(1, n + 1) if n % x == 0]
  • range(1, n + 1) 生成从 1 到 n 的数字序列。
  • if n % x == 0 只保留能整除 n 的数字。

调用 divisors(12) 将会返回 [1, 2, 3, 4, 6, 12]，因为这些数字是 12 的因数。

嵌套的列表推导式

列表推导式还可以用于生成复杂的结构，如处理嵌套的列表。你可以使用两个 for 循环来处理多层结构。

示例：将二维列表展开为一维列表 

matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
flattened = [num for row in matrix for num in row]
  • 第一个 for row in matrix 遍历二维列表的每一行。
  • 第二个 for num in row 遍历每一行中的元素。

结果为 [1, 2, 3, 4, 5, 6, 7, 8, 9]。

使用列表推导式简化复杂逻辑

列表推导式可以帮助简化逻辑复杂的操作。你可以通过多个条件筛选或多个操作生成新的列表，避免冗长的循环和条件嵌套。

示例：同时进行条件判断和操作

假设我们有一个列表，想要筛选出所有大于 10 的偶数并将它们平方：

numbers = [1, 11, 16, 22, 9, 8, 10]
squares = [x**2 for x in numbers if x > 10 and x % 2 == 0]
  • x**2：对满足条件的数进行平方。
  • if x > 10 and x % 2 == 0：仅保留大于 10 且为偶数的元素。

结果为 [256, 484]，因为 16 和 22 符合条件，并且它们的平方分别为 256 和 484。

字符串操作与推导式结合

与列表一样，字符串也可以使用推导式进行操作。你可以将字符串视为字符的序列，对其进行筛选、转换等操作。

示例：将字符串中的所有字母转换为大写 

uppercase_letters = [char.upper() for char in "hello world" if char.isalpha()]
  • char.upper()：将字符转换为大写。
  • if char.isalpha()：只保留字母字符，过滤掉空格和其他符号。

结果为 ['H', 'E', 'L', 'L', 'O', 'W', 'O', 'R', 'L', 'D']。

通过列表推导式，我们可以轻松地处理和生成列表及字符串。它将循环、条件筛选、表达式计算等简洁地组合在一起，极大地提升了代码的可读性和执行效率。不论是在处理数字、字符串，还是在嵌套结构中应用，列表推导式都是 Python 中不可或缺的利器。

Strings 字符串

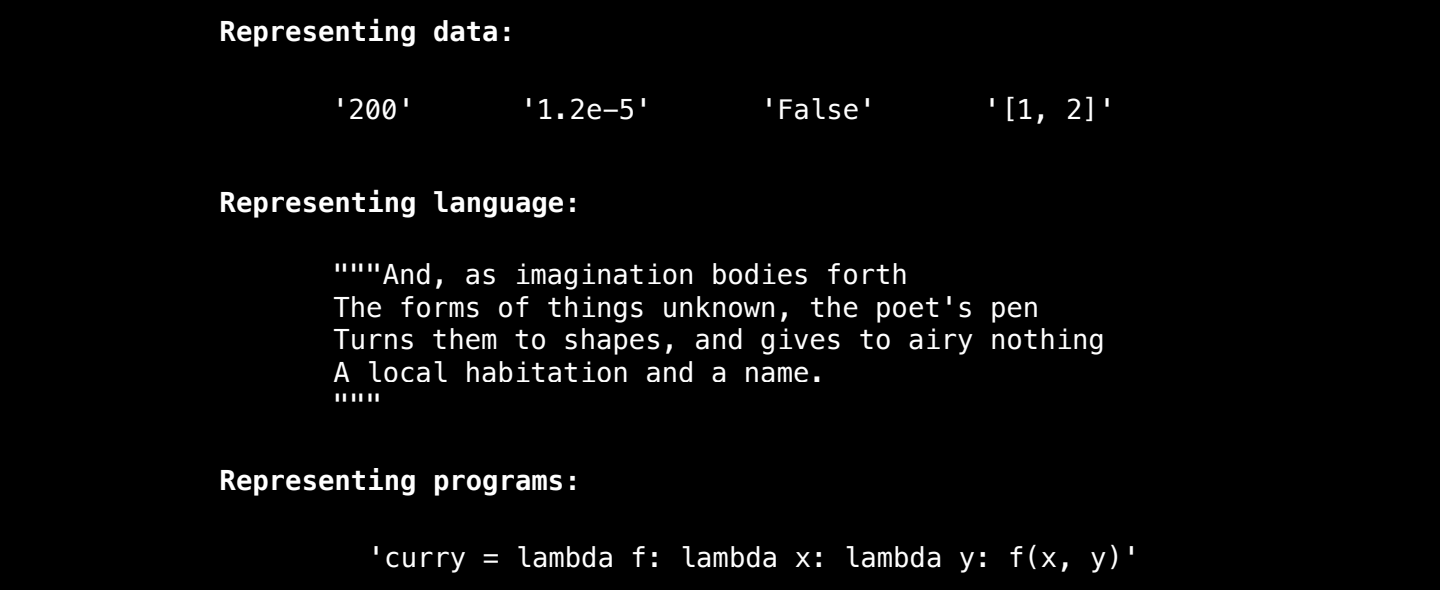
image-20240912104859538

字符串 (Strings) 是 Python 中一种常用的数据类型，用于表示文本数据。字符串可以由单引号、双引号或三引号包裹，用于表示一系列字符的序列。

  • 单引号和双引号：通常用于定义单行字符串。两者之间没有差别，都可以包含字母、数字、符号等。
    • 示例：'Hello' 和 "World" 都是合法的字符串。
  • 三引号：用于定义多行字符串，或作为文档字符串（docstrings）使用，特别适合需要换行的文本内容。
    • 示例： 
      """This is a multi-line
string in Python"""

字符串操作

  1. 字符串作为序列：字符串与列表类似，是一种序列类型。你可以使用 len() 函数获取字符串的长度，并且可以使用索引操作访问其中的特定字符。

    • 示例： 
      city = "Berkeley"
print(len(city))  # 输出: 8
print(city[0])  # 输出: 'B'
print(city[-1])  # 输出: 'y'，负索引从字符串末尾开始计数

  2. 字符串索引返回字符串：当你通过索引访问字符串中的某个元素时，返回的仍然是一个字符串，只不过它的长度为 1。例如，city[0] 返回的是 'B'，而不是一个单独的字符。

  3. 字符串中的 in 操作符：in 操作符不仅能检查元素是否存在于序列中，还可以检查某个子字符串是否存在于另一个字符串中。

    • 示例： 
      sentence = "Where's Waldo?"
print("Waldo" in sentence)  # 输出: True
print("123" in sentence)  # 输出: False

字符串切片（Slicing）

与列表一样，字符串也支持切片操作，用来获取子串。切片的基本语法是 string[start:end:step]，其中 start 是起始索引，end 是结束索引，step 是步长。

  • 示例： 
    name = "Python"
print(name[1:4])  # 输出 'yth'，从索引 1 到 3（不包含 4）
print(name[:3])   # 输出 'Pyt'，从开头到索引 2
print(name[::2])  # 输出 'Pto'，每隔一个字符取一次

切片操作非常灵活，允许你从字符串中提取特定的部分，而无需显式地循环或逐字符处理。

字符串方法

Python 提供了许多内置的方法来处理字符串，如 upper()、lower()、replace() 等。

  • 常用方法：
    • upper() 和 lower()：将字符串转换为大写或小写。 
      print("hello".upper())  # 输出: HELLO
print("WORLD".lower())  # 输出: world
    • replace()：将字符串中的某个子串替换为另一个子串。 
      text = "I love Python"
print(text.replace("love", "like"))  # 输出: I like Python

特殊字符与转义序列

Python 字符串支持使用转义序列来表示特殊字符。这些序列通常以反斜杠 \ 开头，表示一些特殊操作，例如换行、制表符、引号等。

  • 常见的转义字符：
    • \n：换行符，用于在字符串中创建新行。
    • \t：制表符，用于创建水平制表空格。
    • \' 和 \"：分别表示单引号和双引号，用于在字符串中包含引号。
  • 示例： 
    text = "Hello,\nWorld!"
print(text)
# 输出:
# Hello,
# World!

在该示例中，\n 用于表示换行符，所以字符串被分为两行显示。

多行字符串和文档字符串

Python 中可以使用三引号（''' 或 """）来创建多行字符串，这种方式不仅能让字符串跨多行，还可以保留字符串中的格式。通常，三引号也用于函数的文档字符串（docstrings）来描述函数的用途。

  • 多行字符串示例： 
    multiline_string = """This is a 
multi-line string that spans
multiple lines."""
print(multiline_string)

Reversing a String 字符串反转

我们可以用递归的方式来实现字符串的反转。递归的核心思想是将复杂问题逐步简化，直到达到基准情况，然后将结果逐步组合返回。

字符串反转的递归思路

  1. 基准情况：
    • 如果字符串长度为 1 或是空字符串，则直接返回该字符串，因为它已经是反转后的结果。
  2. 递归情况：
    • 对于长度大于 1 的字符串，将第一个字符放到末尾，递归地反转剩下的子字符串。

递归反转字符串的 Python 实现 

def reverse(s):
    # 基准情况：如果字符串长度为0或1，直接返回
    if len(s) <= 1:
        return s
    # 递归情况：反转剩下的字符串并将第一个字符移到末尾
    return reverse(s[1:]) + s[0]

代码解析

  • 基准情况：if len(s) <= 1 检查字符串的长度。如果字符串的长度为 0 或 1，直接返回它自己，因为它已经是反转后的结果。
  • 递归情况：return reverse(s[1:]) + s[0] 将第一个字符 s[0] 移到末尾，并递归地反转其余部分 s[1:]。

示例 

print(reverse("ward"))  # 输出: draw
print(reverse("hello"))  # 输出: olleh

递归过程分析

以 reverse("ward") 为例，递归过程如下：

  1. reverse("ward") 调用 reverse("ard") + "w"
  2. reverse("ard") 调用 reverse("rd") + "a"
  3. reverse("rd") 调用 reverse("d") + "r"
  4. reverse("d") 返回 "d"（基准情况）

然后逐层回溯并组合结果：

  • reverse("rd") 返回 "dr"
  • reverse("ard") 返回 "dra"
  • reverse("ward") 返回 "draw"

最终，递归将字符串 "ward" 反转为 "draw"。

递归思维的关键

递归的核心是简化问题、确定基准情况以及递归组合。在反转字符串的例子中，通过每次去掉字符串的第一个字符并将其放在最后，我们逐步缩小问题规模，直到字符串足够简单（只有 1 个字符或空字符串）。这种逐步缩小问题规模并通过回溯组合结果的过程，是递归算法的本质。

优化递归代码

对于较简单的问题，比如字符串反转，不需要特意分出多个基准情况。我们只需检查字符串长度是否小于等于 1，这样可以同时处理空字符串和单字符的情况，简化代码逻辑，减少不必要的条件分支。