Lecture 11. Data Abstraction

公告

感谢大家录制自己进行期中考试一的过程。如果你还没有收到关于保存期中考试一录音的通知，你可以将其删除。如果你在录制过程中遇到困难，我们已经收到了你相关的笔记，这是没问题的，不会有任何惩罚。我们也会努力改进未来考试的录制流程。大多数人录制时没有遇到问题，但对于那些遇到困难的人来说，这确实很令人沮丧，对此我们深表歉意，我们会努力寻找更好的解决方案。

作业与项目

• 作业二的截止日期是本周四。
• 下周五是“猫”项目（Cats Project）的提交截止日。如果你在周四之前提交，可以获得提前提交的加分。此外，为确保你的进度，你可以在下周二之前完成项目的第一部分，获得一个检查点加分（一分）。该项目涵盖了课程中的多个主题，包括今天的讲座内容以及之前所有的内容。

猫项目简介

“猫”项目测试你的打字速度。该项目有一个命令行接口和一个网页接口，要求你的代码计算打字的准确率和速度。接下来我们演示一下：

我打字时犯了很多错误，准确率只有87.5%。如果能够在我打字时自动纠正错误岂不是很好？启用自动更正功能后，当我输入错误时，系统会尝试根据我已经输入的内容来猜测我本应该输入的内容。不过，它并不根据你原本打算输入的内容进行更正，而是基于你输入到目前为止的内容进行猜测。结果可以看到，启用自动更正后，我的准确率提高了许多。如果我输入了一个正确的单词，比如“wit”，系统不会进行更正；但如果输入了无效的字符或单词，系统会尝试进行更正，甚至能够纠正比较复杂的错误。

在这个项目中，你需要使用递归、容器以及数据抽象来实现程序。

Data Abstraction 数据抽象

接下来我们讲解数据抽象的概念。大多数值都是复合值，意味着它们将多个对象组合在一起，形成一个具有多个部分的对象。例如，日期由年月日组合而成，地理位置由经度和纬度构成。抽象数据类型允许我们将复合对象作为一个整体来操作，这是抽象的一种形式。

数据抽象的核心思想是，将数据的表示方式与数据的操作方式隔离开来。这样我们就可以分别处理程序中的两个部分，即如何表示数据和如何使用数据。通过这种方法，我们可以将程序的不同关注点分离开来，修改数据表示时不会影响数据的使用，反之亦然。数据抽象是一种方法论，它通过函数在数据的表示和使用之间建立抽象屏障。

虽然所有程序员都会在某个时候处理复合数据，但优秀的程序员会通过使用数据抽象，使程序更加模块化。你们很快也会成为优秀的程序员。让我们来看一个例子——有理数，以更好地理解数据抽象。

Rational Numbers 有理数的例子

有理数可以表示为分子（numerator）除以分母（denominator），两者均为整数。由于整数可以精确表示，因此我们可以准确地表示分数。例如，1/3 是一个准确的分数表示。但是，一旦我们实际进行除法运算，例如 1 ÷ 3，结果将会是一个浮点数，这只能是分数的近似值，因为计算机中浮点数通过二进制扩展表示，并不能完全精确。

为了避免这种近似表示，我们希望将分子和分母分开存储，而不是直接进行除法。我们可以定义一个复合数据类型来表示有理数。假设我们有以下函数：

• rational(n, d)：接受两个整数 n（分子）和 d（分母），并返回一个复合数据类型 x，表示有理数。
• numer(x)：返回有理数 x 的分子。
• denom(x)：返回有理数 x 的分母。

通过这些函数，我们可以组合一个分子和一个分母，生成一个有理数的实例。rational 函数是一个构造函数（constructor），它用于创建复合数据类型的新值。而 numer 和 denom 函数是选择器（selectors），用于从复合数据类型中提取部分数据。

操作有理数

我们可以利用这些构造函数和选择器来编写其他操作有理数的函数，例如加法和乘法。举个例子：

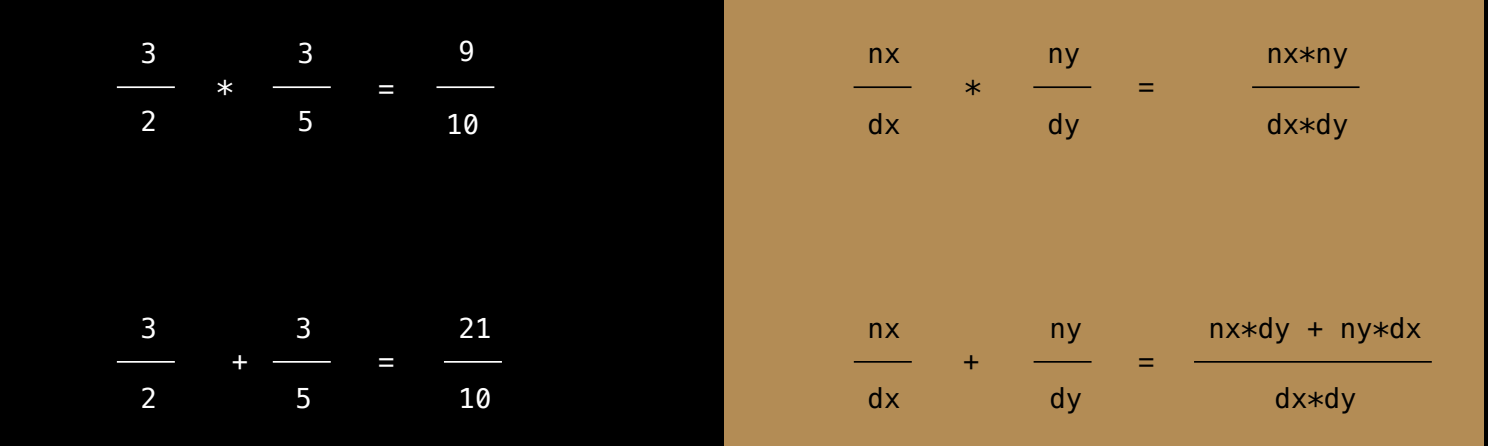
• 乘法：假设我们要将两个有理数 3/2 和 3/5 相乘，结果是 9/10。这是因为有理数乘法的通用公式是：结果的分子等于两个有理数的分子相乘，结果的分母等于两个有理数的分母相乘。

• 加法：加法稍微复杂一些。举例来说，3/2 + 3/5 = 21/10。如何得出这个结果？一般来说，有理数加法的公式是：将第一个有理数的分子乘以第二个有理数的分母，加上第二个有理数的分子乘以第一个有理数的分母，再除以两个有理数的分母相乘的结果。

通过这些操作，我们可以轻松地处理有理数的各种运算，同时保持程序的模块化和简洁性。这正是数据抽象的力量所在。

有理数的操作实现

我们已经讨论了如何定义有理数的乘法和加法。具体来说：

乘法

有理数的乘法遵循以下公式：

• 结果的分子是两个有理数的分子相乘的结果。
• 结果的分母是两个有理数的分母相乘的结果。

现在，我们来看一下如何通过代码实现这个公式。我们将使用构造函数和选择器来定义这个函数：

def multiply_rational(x, y):
    return rational(numer(x) * numer(y), denom(x) * denom(y))

在这个代码片段中：

• numer(x) 和 numer(y) 分别获取有理数 x 和 y 的分子。
• denom(x) 和 denom(y) 分别获取有理数 x 和 y 的分母。
• 最终，通过 rational 函数来构造一个新的有理数，其分子是两个输入分子的乘积，分母是两个输入分母的乘积。

加法

有理数的加法稍微复杂一些。加法的通用公式是：

• 结果的分子等于第一个有理数的分子乘以第二个有理数的分母，加上第二个有理数的分子乘以第一个有理数的分母。
• 结果的分母等于两个有理数的分母相乘。

实现加法的代码如下：

def add_rational(x, y):
    new_numerator = numer(x) * denom(y) + numer(y) * denom(x)
    new_denominator = denom(x) * denom(y)
    return rational(new_numerator, new_denominator)

在这个函数中：

• new_numerator 是通过上述公式计算得到的新的分子。
• new_denominator 是两个有理数分母的乘积。
• 最后，通过 rational 构造函数返回新的有理数。

判等函数

为了判断两个有理数是否相等，我们不能仅仅比较它们的分子和分母。例如，1/2 和 2/4 虽然分子和分母不同，但它们表示相同的值。因此，我们需要一个判等函数，它比较两个有理数的实际值。这个判等的规则是：

• 如果 x 和 y 是两个有理数，x 的分子乘以 y 的分母应等于 y 的分子乘以 x 的分母。

实现代码如下：

def equal_rational(x, y):
    return numer(x) * denom(y) == numer(y) * denom(x)

Pairs

我们已经定义了乘法、加法和判等的函数，所有这些操作都基于构造函数和选择器，它们共同实现了有理数的抽象数据类型。尽管我们还没有具体实现这些函数，但通过这种抽象，我们可以先定义如何使用它们，再实现这些底层的函数。

使用列表来表示有理数

为了实现有理数的构造函数 rational，我们需要一种表示两个整数（分子和分母）的方法。在 Python 中，可以使用列表来表示一对值。

def rational(n, d):
    """Construct a rational number that represents N/D."""
    return [n, d]

在这个例子中，rational 函数返回一个包含两个整数 n 和 d 的列表，用来表示有理数。

接下来，我们需要定义如何获取有理数的分子和分母。假设有理数 x 是通过 rational 函数创建的列表，我们可以通过列表的索引来访问它的元素：

def numer(x):
    """Return the numerator of rational number X."""
    return x[0]

def denom(x):
    """Return the denominator of rational number X."""
    return x[1]

在这里：

• numer(x) 返回列表 x 的第一个元素，即分子。
• denom(x) 返回列表 x 的第二个元素，即分母。

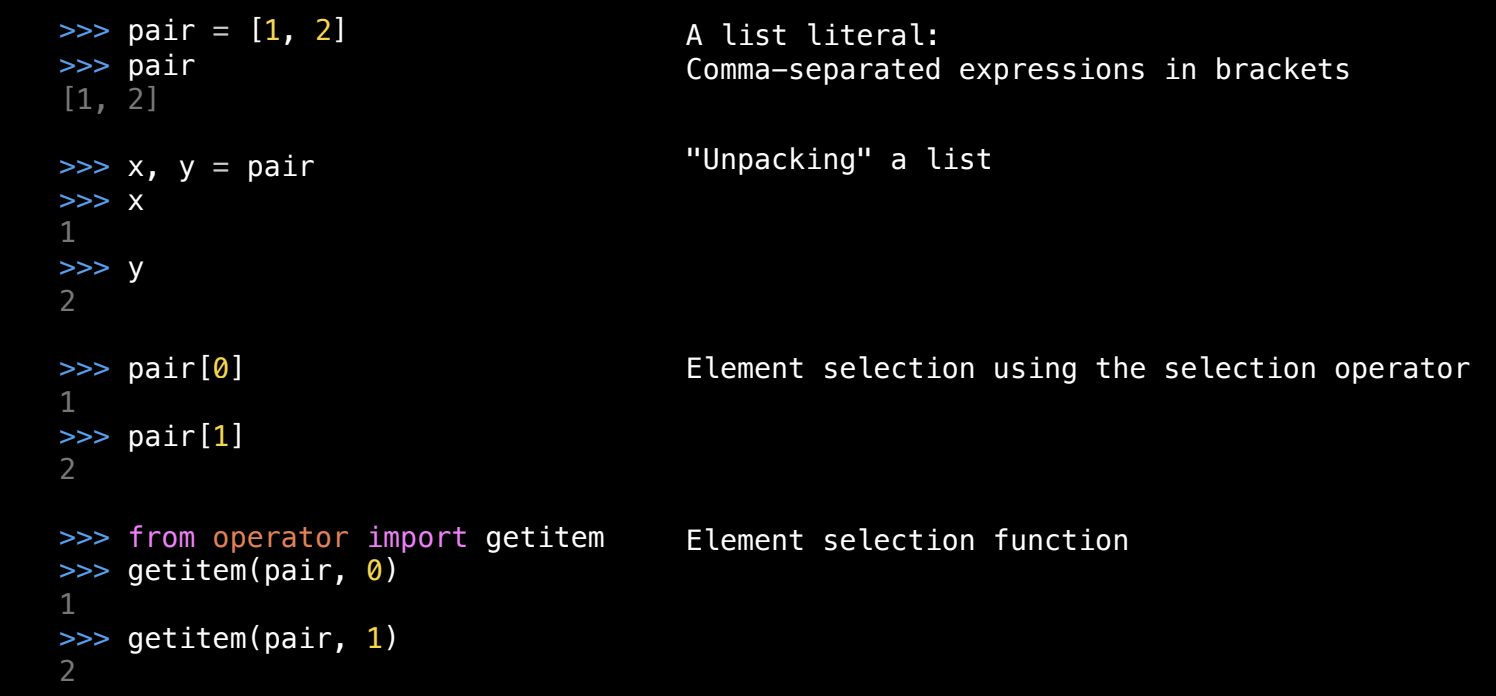
列表解包与元素选择

Python 中可以通过解包列表将其元素绑定到不同的变量。例如：

pair = [1, 2]
x, y = pair

在这个例子中，x 将被绑定到列表的第一个元素 1，y 将被绑定到列表的第二个元素 2。这就是我们从列表中提取值的方式之一，称为解包。

另外，我们还可以使用元素选择操作符（[]）来访问列表中的元素：

pair[0]  # 返回 1
pair[1]  # 返回 2

在 Python 中，还有一个函数 get_item 可以完成同样的操作：

import operator
operator.getitem(pair, 0)  # 返回 1
operator.getitem(pair, 1)  # 返回 2

这种访问列表元素的方式为我们提供了灵活性，使我们能够方便地操作数据。

通过将有理数的分子和分母打包成一个列表，我们实现了有理数的抽象数据类型。构造函数 rational 用于创建有理数，而选择器 numer 和 denom 用于提取有理数的分子和分母。通过这些函数，我们可以实现有理数的加法、乘法以及判等操作，从而实现模块化和抽象的设计。

数据抽象的进一步讨论：有理数的最简化表示

我们之前定义了有理数的乘法和加法操作，但忽略了一个关键点：有理数的表示应该是最简分数。例如，3/2 × 5/3 应该得到 5/2 而不是 15/6，因为 15/6 并不是最简的形式。

有理数化简为最简形式

我们可以通过引入最大公约数（GCD, Greatest Common Divisor），将有理数化简为最简形式。这样可以确保分子和分母总是互质（即最大公约数为 1）。在 Python 中，math 模块提供了一个内置的函数 gcd 来计算两个数的最大公约数。

修改构造函数

我们现在需要修改 rational 构造函数，使其能够自动将分子和分母化简为最简形式：

import math

def rational(n, d):
    """Construct a rational that represents n/d in lowest terms."""
    g = math.gcd(n, d)  # 计算分子和分母的最大公约数
    return [n // g, d // g]  # 将分子和分母除以最大公约数，保证最简

在这个构造函数中：

• math.gcd(n, d) 计算分子 n 和分母 d 的最大公约数 g。
• 然后，我们将分子和分母分别除以 g，并返回一个表示有理数的列表。

获取分子和分母

对于已经通过 rational 构造函数创建的有理数，我们仍然可以使用之前定义的选择器来获取分子和分母：

def numer(x):
    return x[0]  # 返回分子

def denom(x):
    return x[1]  # 返回分母

示例：有理数的乘法和加法

通过这种方式，我们可以确保所有有理数的表示都是最简形式。例如，考虑以下乘法和加法运算：

乘法

x = rational(3, 2)
y = rational(5, 3)
result = multiply_rational(x, y)  # 结果应该是 [5, 2] 而不是 [15, 6]

乘法仍然按照我们之前定义的方式进行，但由于构造函数对结果进行了化简，返回的结果是 5/2 而不是 15/6。

加法

同理，假设我们要计算 2/5 + 1/10：

x = rational(2, 5)
y = rational(1, 10)
result = add_rational(x, y)  # 结果是 [1, 2] 而不是 [25, 50]

由于 25/50 可以化简为 1/2，最终结果为 1/2。

通过使用 gcd 函数，我们可以确保所有有理数的分子和分母总是互质的，这不仅简化了有理数的表示形式，还使得操作更加高效。

Abstraction Barriers 抽象屏障

我们在实现有理数时，使用了构造函数 rational 和选择器 numer、denom 来创建和操作有理数。在这一过程中，抽象屏障（abstraction barriers）的概念起到了非常重要的作用。它帮助我们将程序的不同部分隔离开来，使每一部分只需关心它应该处理的内容，而不必深入了解具体的数据表示方式。

抽象屏障确保我们在编写使用有理数的程序时，只通过构造函数和选择器操作这些数据，而不是直接操作它们的底层表示（例如，列表）。具体来说：

• 程序的使用层：在上层使用有理数进行运算时（如加法、乘法等），我们只需使用 rational、numer 和 denom 等函数，不需要关心有理数是如何存储的。这一层不应该直接操作底层表示，而是遵循定义好的抽象接口。
• 程序的实现层：在实现构造函数和选择器时，我们可以使用底层的数据表示（如列表），但这仅限于构造和选择操作的实现，不应暴露给上层程序。

为什么需要遵守抽象屏障

1. 可维护性：通过遵守抽象屏障，我们可以在不影响其他部分的情况下更改数据的表示方式。例如，如果我们决定将有理数从列表表示改为其他结构（如元组），只需要修改 rational、numer 和 denom 函数，而不需要重写所有使用有理数的代码。

2. 模块化设计：抽象屏障使得每个模块只处理与它相关的任务，避免了跨层干涉。这种设计提高了程序的模块化程度，使得代码更易于理解、维护和扩展。

违反抽象屏障的后果

在违反抽象屏障的情况下，程序的各个部分可能直接依赖于数据的底层表示，这会导致以下问题：

• 缺乏灵活性：如果有理数的表示方式发生变化，所有依赖于底层表示的代码都需要修改，导致代码维护困难。
• 代码冗余和不一致：不同部分的程序可能以不一致的方式操作有理数，从而引入错误。

示例：违反抽象屏障

def add_rational(x, y):
    return [numer(x) * denom(y) + numer(y) * denom(x), denom(x) * denom(y)]

上面代码是错误的，因为它直接返回了一个列表 [numer, denom]，而没有使用 rational 构造函数。假设我们更改了 rational 的实现（例如，使用元组代替列表），这段代码将无法正确工作，因为它直接依赖于有理数是列表的假设。这种情况下，程序不仅缺乏灵活性，还难以维护。

正确的实现应该是：

def add_rational(x, y):
    return rational(numer(x) * denom(y) + numer(y) * denom(x), denom(x) * denom(y))

在这个实现中，使用了 rational 构造函数，无论底层表示如何变化，代码都能够正常工作。

数据抽象 数据表示与行为

数据抽象的关键思想是：我们通过行为来识别数据，而不是通过其具体的实现细节。对于有理数来说，只要构造函数和选择器的行为符合预期，数据表示就是有效的。

数据行为条件

我们可以用以下行为条件来描述有理数的抽象：

• 如果我们通过分子 n 和分母 d 构造了有理数 x，那么它应该满足以下行为：

  numer(x) / denom(x) == n / d
  

也就是说，通过 rational(n, d) 构造出来的有理数，应该表现得像一个有理数，无论底层表示是列表、元组还是其他结构。只要行为一致，底层实现方式可以自由更改。

数据抽象：构造函数与选择器的行为

数据抽象的核心思想是通过构造函数和选择器来定义数据的行为，而不必关心其具体表示方式。只要行为条件满足，数据的表示方式就是有效的。这意味着我们可以通过行为而非具体实现来识别数据类型。

我们已经定义了有理数的加法、乘法和相等性检测等操作。这些操作依赖于构造函数 rational 和选择器 numer、denom 来操作有理数，而不会对底层的数据表示方式做任何假设。这使得代码灵活且易于维护，因为它只依赖于抽象接口，而不是具体实现。

现在我们展示如何通过改变有理数的表示方式而不影响程序的行为。之前，我们使用列表来存储分子和分母。接下来，我们将不再使用列表，而是使用函数来实现相同的抽象。

使用函数代替列表

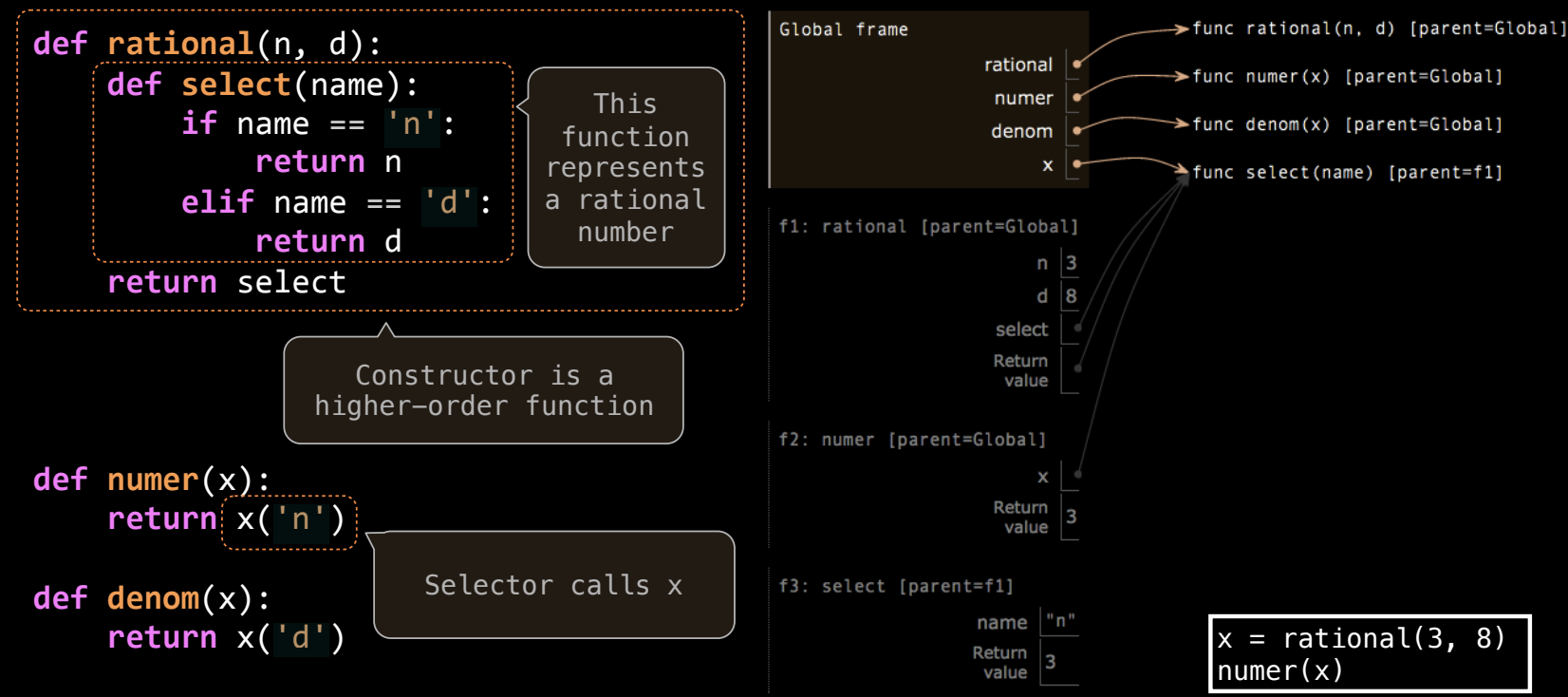
我们可以通过定义一个选择函数 select 来实现有理数的表示。这个选择函数根据输入的参数返回相应的分子或分母。以下是构造函数 rational 的实现：

def rational(n, d):
    def select(name):
        if name == 'n':
            return n
        elif name == 'd':
            return d
    return select

在这个实现中：

• rational 函数返回一个选择器函数 select，它根据传入的参数返回分子或分母。
• 如果传入参数是 'n'，则返回分子 n；如果是 'd'，则返回分母 d。

选择器的实现

选择器 numer 和 denom 使用选择函数来获取分子和分母：

def numer(x):
    return x('n')

def denom(x):
    return x('d')

在这里：

• numer(x) 调用选择函数 x 并传入 'n'，以此获取分子。
• denom(x) 调用选择函数 x 并传入 'd'，以此获取分母。

验证新的表示方式

我们可以使用新的表示方式来计算有理数的乘法和加法，代码仍然可以正常工作，因为所有的操作都是通过构造函数和选择器实现的，而不是依赖于底层的具体表示方式。

x = rational(1, 2)  # 表示 1/2
y = rational(3, 8)  # 表示 3/8
result = multiply_rational(x, y)  # 结果应该是 3/16
print(numer(result), "/", denom(result))  # 输出 3 / 16

即使我们将有理数的表示方式从列表更改为函数，程序仍然能够正确处理有理数的运算。这是因为我们遵循了数据抽象的原则，只通过构造函数和选择器操作数据，而不依赖具体表示方式。

函数表示的工作原理

通过使用函数来表示有理数，我们利用了函数的闭包特性。构造函数 rational 返回的 select 函数能够“记住”其外部作用域中的分子 n 和分母 d，即使构造函数已经执行完毕。选择器 numer 和 denom 可以调用这个闭包，从而获取保存的分子和分母。

这使得我们不再依赖列表或任何内置的数据类型，而是通过纯函数实现有理数的存储和操作。这种表示方式同样满足数据抽象的要求，因为它依然实现了预期的行为。

正如之前所讨论的，抽象屏障确保了程序的不同部分只使用合适的抽象级别进行操作，而不跨越这些界限。具体到有理数的实现，抽象屏障允许我们自由更改数据的表示方式，而不会影响依赖于这些抽象接口的其他代码。

如果我们在操作有理数时直接依赖于其底层的表示方式（例如，直接操作列表元素而不是使用选择器 numer 和 denom），则会引入违反抽象屏障的风险。例如，假设我们直接从列表中提取元素，而不是使用选择器：

# 错误的做法：直接操作列表
def add_rational(x, y):
    return [x[0] * y[1] + y[0] * x[1], x[1] * y[1]]

这种实现依赖于有理数是以列表表示的假设。如果我们将有理数改为用函数表示，这段代码将无法正常工作。因此，违反抽象屏障会导致代码难以维护，并且无法适应底层表示的变化。

字典（Dictionary）

Python 中的字典（dictionary）是一种用于存储键值对的无序数据结构。每个键（key）唯一地映射到一个值（value），并且通过键来访问其对应的值。以下是字典的基本功能和使用方法：

字典的创建与键值对选择

• 字典使用大括号 {} 创建，其中键和值使用冒号 : 分隔，多个键值对用逗号 , 分隔。

numerals = {'X': 10, 'V': 5, 'I': 1}

在上面的例子中，'X' 是键，10 是与之对应的值，依此类推。要选择某个键的值，可以使用键作为索引：

print(numerals['X'])  # 输出 10

• 不能通过值来查找键。比如 10 是一个值，而不是键，因此无法使用它来进行查找。

字典的方法

1. 获取所有键、值和键值对：
   • keys() 方法返回字典中的所有键。
   • values() 方法返回字典中的所有值。
   • items() 方法返回字典中的所有键值对，表示为元组的列表。

print(numerals.keys())    # 输出：dict_keys(['X', 'V', 'I'])
print(numerals.values())  # 输出：dict_values([10, 5, 1])
print(numerals.items())   # 输出：dict_items([('X', 10), ('V', 5), ('I', 1)])

1. 通过 dict() 构造函数创建字典：
   • 你可以使用键值对的列表通过 dict() 函数创建一个新的字典。

items = [('X', 10), ('V', 5), ('I', 1)]
numerals = dict(items)
print(numerals['X'])  # 输出 10

1. 检查键是否存在于字典中：
   • 可以使用 in 关键字来检查某个键是否在字典中。

print('X' in numerals)  # 输出 True
print('Z' in numerals)  # 输出 False

1. 使用 get() 方法获取值：
   • get() 方法允许在键不存在时提供默认值。

print(numerals.get('X', 0))      # 输出 10，因为 'X' 存在
print(numerals.get('Z', 0))      # 输出 0，因为 'Z' 不存在

字典推导式（Dictionary Comprehension）

字典推导式允许你以简洁的方式创建字典，类似于列表推导式。下面是一个将数字和它们的平方关联起来的字典推导式示例：

squares = {x: x**2 for x in range(10)}
print(squares[7])  # 输出 49

字典的限制

1. 键的唯一性：
   • 字典中的每个键必须是唯一的。如果在创建或更新字典时使用了相同的键，最后一个键值对将覆盖之前的键值对。

numerals = {'X': 10, 'X': 20}
print(numerals)  # 输出 {'X': 20}

1. 键的类型要求：
   • 键必须是不可变类型（immutable types），例如整数、字符串或元组。列表或字典等可变类型不能作为字典的键，因为它们的值可以改变，这会破坏字典内部哈希表的结构。

# 错误示例：列表不能作为键
invalid_dict = {[1]: 2}  # 会引发 TypeError: unhashable type: 'list'

字典的特性总结

• 字典是无序的，这意味着键值对的插入顺序不会影响字典中的顺序，也不应依赖于插入顺序。
• 键必须是不可变类型，且在字典中不能重复。
• 如果需要为某个键关联多个值，可以将这些值存储在一个序列（如列表或元组）中，作为字典的值。

# 关联多个值
numerals = {'X': [10, 15], 'V': [5, 7]}
print(numerals['X'])  # 输出 [10, 15]

字典是 Python 中一种非常强大的数据结构，允许你通过键来快速查找对应的值。通过 get() 方法可以安全地获取值，并提供默认值以避免错误。字典的灵活性来自于它可以存储不同类型的值，并且可以通过字典推导式轻松创建复杂的映射关系。虽然键必须是不可变类型，但字典的值可以是任意类型，包括列表和其他字典。

字典的这些特性使其在处理映射关系时非常有用，但要注意保持键的唯一性和不可变性，以确保字典的稳定性和正确性。