Lecture 13. Binary Numbers

Announcements

1. 项目截止日期：
   • CATS 项目的截止日期是周五。
   • 第一阶段的任务需要在周二之前完成，以获得检查点的 1 分。
   • 如果你能在周四之前提交整个项目，可以获得提前提交的额外加分。
2. 课堂讲座：
   • 今天和周三的讲座不会出现在考试或作业中，但内容非常有趣，值得学习。这些知识将在未来的课程中再次出现，现在的学习将有助于加深你对计算机如何表示程序的理解。

课程内容概述

1. 抽象的力量：
   • 这学期的大部分时间我们都在讨论 Python 数据结构、算法、类和面向对象编程。其中一个重要的主题是抽象的力量。
   • 抽象可以帮助我们将复杂的数据或代码进行模块化处理，使得我们不需要关注底层细节，从而更加高效地编写代码。
2. 计算机作为终极抽象：
   • 计算机本身就是一种极强的抽象工具。我们日常使用计算机进行各种操作，如保存文件或进行数值计算，但我们通常并不知道计算机的内部工作机制。
   • 在接下来的课程中，我们将探讨计算机的基本构建模块，并了解现代计算机的工作原理。

计算机的基础：二进制数与进制转换

十进制数的复习：

• 我们日常使用的数字是十进制，这意味着每个数字的位数是基于 10 的幂次。例如，数字 723 可以表示为： \[ 7 \times 10^2 + 2 \times 10^1 + 3 \times 10^0 \]
• 每个数字在相应的位数上表示为该位数的数值乘以 10 的幂。

进制的多样性：

• 虽然我们默认使用十进制，但其他进制系统在历史上也被广泛使用。例如，有些文明使用八进制（Base-8）。
• 例如，八进制的 257 表示为： \[ 2 \times 8^2 + 5 \times 8^1 + 7 \times 8^0 \]
• 在这里，基数是 8，而不是 10。

课程目标

理解现代计算机的核心构造：

• 在接下来的课程中，我们将逐步了解现代计算机的基本构建块，如二进制数和逻辑运算。
• 尽管我们不会深入探讨所有复杂的细节，但你将学到足够的知识，以理解计算机如何执行从简单加法到复杂程序的各种计算。

进制转换（以八进制为例）

从八进制转换到十进制的过程：

• 八进制的基数是8，而不是常见的10。
• 将数字 257 八进制转为十进制：
  • \(2 \times 8^2 + 5 \times 8^1 + 7 \times 8^0\)
  • 计算结果：\(2 \times 64 + 5 \times 8 + 7 = 128 + 40 + 7 = 175\)。

  这个过程与十进制类似，只是基数从10变成了8，指数释如何将其转换为十计算规则保持不变。通过这一过程，讲者展示了如何通过简单的算术操作在不同进制系统之间进行转换。

不同的进制系统是任意的，没有任何进制本质上比其他进制更“正确”或“错误”。进制系统的选择仅影响数字的表示形式，而不改变数字的本质。类似于我们在公制和英制单位之间的转换（例如温度、距离、重量的转换），我们也可以在不同进制之间进行转换。

二进制系统

• 二进制的基数是2，只有两个数字：0 和 1。
• 在二进制中，任意数字都可以表示为一组 0 和 1。与十进制不同，二进制只用到了两个符号。

以二进制数 0110 为例，将其转换为十进制：

• 这个二进制数表示为：
  • \(0 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 0 \times 2^0\)
  • 计算结果：\(0 \times 8 + 1 \times 4 + 1 \times 2 + 0 = 4 + 2 = 6\)。

限制位数的二进制表示

位数的限制对于二进制数的影响：

• 例如，一个两位的二进制数只能表示 0 到 3 的值：
  • 00（二进制） = 0（十进制）
  • 01（二进制） = 1（十进制）
  • 10（二进制） = 2（十进制）
  • 11（二进制） = 3（十进制）

与十进制相似，限制位数也会限制可表示的数的范围。如果在十进制中限制为两位数，则只能表示 0 到 99 的数，无法表示 100 及以上的数字。

二进制位数的影响

• 二进制中的位数决定了可以表示的数的范围。一个 \(n\) 位的二进制数可以表示从 0 到 \(2^n - 1\) 的数字。例如，三位二进制数可以表示的最大数字是 \(2^3 - 1 = 7\)：
  • 000（二进制） = 0（十进制）
  • 001（二进制） = 1（十进制）
  • 010（二进制） = 2（十进制）
  • 011（二进制） = 3（十进制）
  • 100（二进制） = 4（十进制）
  • 101（二进制） = 5（十进制）
  • 110（二进制） = 6（十进制）
  • 111（二进制） = 7（十进制）
• 例如，对于二进制数 101，其表示的十进制数为： \[ 101_2 = 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 = 4 + 0 + 1 = 5_{10} \]

熟悉二的幂次

• 作为计算机科学家，必须对二的幂次非常熟悉，因为它是二进制计算的基础。常用的二的幂次包括： \[ 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 \]
• 这些幂次不仅在二进制运算中有重要作用，在计算机存储容量（如内存、硬盘）和其他计算机科学的概念中也广泛应用。

二进制与十进制的转换

三位二进制数的计算： 以三位二进制数 101 为例，解释如何将二进制数转换为十进制： \[ 101_2 = 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 = 4 + 0 + 1 = 5_{10} \]

• 2^2 = 4，表示第一个位置的 1；
• 2^1 = 2，对应的值为 0，所以忽略；
• 2^0 = 1，表示最后一个位置的 1。

通过这种方式可以验证，二进制数 101 对应的十进制值是 5。

四位二进制数的范围：

• 四位二进制数的最大值是 \(2^4 - 1 = 15\)，最小值是 0。对应的二进制表示从 0000 到 1111。
• 以二进制数 1011 为例，讲者解释如何将其转换为十进制： \[ 1011_2 = 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 = 8 + 0 + 2 + 1 = 11_{10} \]
• 通过类似的步骤，可以将任何四位二进制数转换为对应的十进制值。

为什么计算机使用二进制？

计算机之所以采用二进制系统，是因为其硬件结构更适合处理只有两个状态（0 和 1）的数据。为了更深入地理解计算机如何进行二进制运算，首先需要理解这些数在不同位数下的表示方式。

二进制的可靠性： 为什么计算机采用二进制系统，而不是十进制或其他进制。核心原因是二进制在物理实现上更加可靠：

• 计算机中的信息以电子的形式存储，电子信号可能会受到噪声或其他因素的干扰，使得信号不够稳定。如果我们使用十进制系统，则需要区分 10 个不同的电平（如 0 到 9），每个电平的区分会非常精细，容易因为噪声造成错误。
• 相比之下，二进制只需区分两个状态：0 和 1。即使有一些小的波动，区分这两种状态也相对容易，因此更适合计算机系统。

类比说明：

• 假设有一个试管，里面可以装水。如果用十进制表示，那么水位可以是从 0 到 9 的任意一个高度。如果水位稍有波动，数字可能会从 7 变成 6 或 8，这样就会导致错误。
• 但如果只区分水满（1）或空（0），即使有一些波动，也可以很容易地判断状态是 0 还是 1。

下一步：负数的表示

如何表示负数：

• 由于计算机只能处理 0 和 1，因此无法直接在数字前加负号（不像手写的代数表达式可以直接加上负号）。
• 下一步将介绍如何通过二进制系统来表示负数，并继续探讨如何表示浮点数和其他复杂的数据类型。

负数的二进制表示

引入问题：无负号表示

• 在计算机中，无法像在纸上写代数那样直接在数字前加一个负号，因为计算机只能处理 0 和 1 两种状态。
• 因此，需要通过二进制的0 和 1来表示正数和负数，并进行一些额外的编码操作。

简单的符号位表示法：

• 一种最直观的方法是使用二进制数的最高位（最左边的一位）作为符号位：
  • 0 表示正数；
  • 1 表示负数。
• 例如，对于三位有符号的二进制数：
  • 正数部分（符号位为 0）：\( 000_2, 001_2, 010_2, 011_2 \) 对应 \( 0, 1, 2, 3 \)；
  • 负数部分（符号位为 1）：\( 100_2, 101_2, 110_2, 111_2 \) 对应 \( -0, -1, -2, -3 \)。

符号位表示的局限性：

• 符号位方法看似简单易懂，但存在负零的问题：\(000_2\) 和 \(100_2\) 分别表示正零和负零，这在数学上并无实际意义。
• 另外，这种表示方法的计算效率不高，对于计算机来说也较为繁琐。因此，尽管符号位方法在概念上容易理解，实际应用中并不是最佳选择。

二进制的补码表示法

引入补码表示法：

• 为了解决符号位表示法中的问题，计算机使用了二进制补码（Two’s Complement）来表示正数和负数。
• 在补码表示法中，正数的表示与无符号数相同，而负数则通过翻转正数的位（取反）并加 1 来表示。

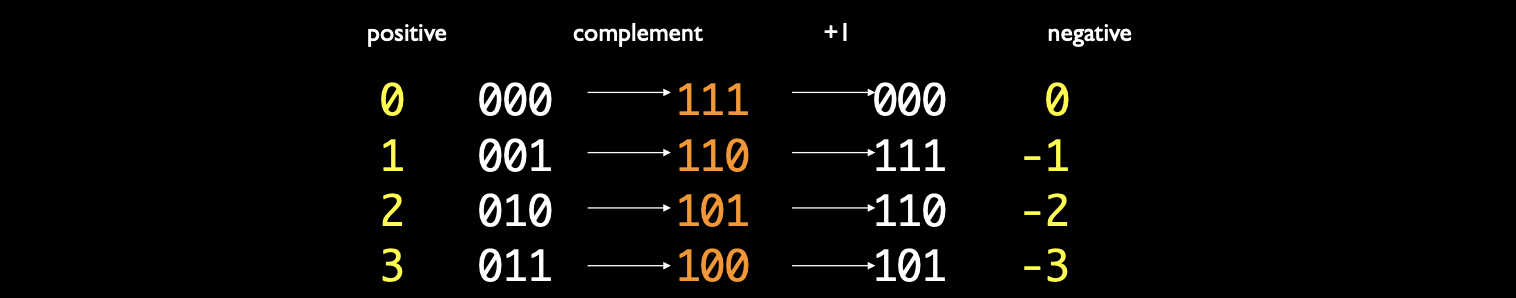
补码的计算步骤：

• 正数的表示：
  • 例如，三位二进制数 6 用四位二进制表示为 \( 0110_2 \)： \[ 0110_2 = 2^2 + 2^1 = 4 + 2 = 6_{10} \]
• 负数的表示：
  • 要得到 -6，首先对 6 的二进制数进行逐位取反（补码）： \[ 0110_2 \quad \text{取反} \quad 1001_2 \]
  • 然后再加 1： \[ 1001_2 + 1 = 1010_2 \] 所以，-6 的补码表示为 \( 1010_2 \)。

为什么补码有效？

• 符号位一致性：补码中的最高位（最左边的一位）仍然表示符号位——1 表示负数，0 表示正数。
• 消除负零：通过补码表示，负零的问题消失了，因为 \(0000_2\) 表示 0，而没有单独的负零表示。
• 便于计算：补码表示的最大优势在于它简化了二进制加减法操作。在补码表示下，计算机可以使用相同的加法电路来处理加法和减法运算，不需要额外的减法逻辑。

补码的计算实例：

• 让我们再看一个例子，用三位二进制表示 -3：
  • 正数 3 的二进制表示为 \( 011_2 \)。
  • 对其取反，得到 \(100_2\)。
  • 加 1，得到 \(101_2\)，即 -3 的补码表示为 \(101_2\)。

为什么补码对计算机有用？

简化计算：

• 虽然对人类而言，补码表示可能稍显复杂，但对于计算机来说，它极大地简化了加法和减法运算。使用补码，计算机无需额外的减法运算电路，因为加法和减法可以使用相同的逻辑处理。

唯一的零表示：

• 另一个补码的好处是，它消除了符号位表示法中的“正零”和“负零”的矛盾情况，使零的表示唯一，从而避免了重复。

缺失的数：补码范围问题

补码系统中的数值范围：

• 在三位二进制补码系统中，可以表示的数值范围为 \(-4\) 到 \(3\)。正数部分包括 \(0, 1, 2, 3\)，负数部分包括 \(-1, -2, -3, -4\)。
• 由于三位补码数的表示范围是 \(-2^{n-1}\) 到 \(2^{n-1} - 1\)，所以当使用三位二进制补码时，能表示的最大负数是 \(-4\)（即 \(100_2\)），而不是 -8 或其他。

缺失的数解释：

• 我们在三位补码系统中可以表示的数为 \(7\) 个，而不是传统的 \(8\) 个，这是因为最高位的一个数（\(100_2\)）被用来表示最小的负数 \(-4\)，因此少了一个正数。
• 100_2 对应的补码数值是 \(-4\)，而不是其他更大的正数。

补码运算实例

加法运算实例：2 + 2：

• 让我们首先进行一个无符号的二进制加法运算。将两个二进制数 \(0010_2\) 和 \(0010_2\) 相加： \[ 0010_2 + 0010_2 = 0100_2 \] 结果为 \(0100_2\)，即 4。这与十进制的加法一致，二进制的加法操作类似于十进制加法，只是进位规则不同。

旧式符号位表示法的加法问题：2 + (-2)：

• 使用旧的符号位表示法，我们可以通过简单地改变符号位来表示负数。比如，\(0010_2\) 是正数 2，而 \(1010_2\) 是负数 -2。
• 如果尝试将二者相加： \[ 0010_2 + 1010_2 = 1100_2 \] 结果为 \(1100_2\)，但这个结果并不代表零，这是因为符号位和数值位混在一起，导致加法操作无效。

补码系统下的加法：2 + (-2)：

• 在补码系统中，加法运算非常自然且有效。我们首先计算 \(-2\) 的补码：
  • \(2_2\) 的二进制表示为 \(0010_2\)。
  • 取反 \(1101_2\)，加 1 得到 \(-2\) 的补码表示 \(1110_2\)。
• 现在我们将 \(2_2\) 和 \(-2_2\) 相加： \[ 0010_2 + 1110_2 = 0000_2 \] 结果为 \(0000_2\)，即 0。这是期望的结果。

溢出问题：

• 在补码运算中，如果结果的进位超出了规定的位数（例如四位数的第五位），则称为溢出。这些多余的位会被丢弃，不影响计算结果。补码系统中，溢出位的处理是非常自然的，不需要特别关心溢出位。
• 计算 \(1+1=2\) 时，在二进制中，2 表示为 \(10_2\)，因此会发生进位。例如，在进行补码运算时，如果最终得到的结果超过了系统的最大表示位数，会产生溢出位，但这个溢出位会被忽略。
• 例如，在三位补码系统中，计算 \(2 + (-2)\) 时，最高位的进位将被丢弃，产生正确的结果 0。

如何处理不同表示法下的二进制数

区分无符号数与补码数：

• 当我们看到一个二进制数时，必须明确它的表示法。比如，四位的二进制数 \(0111_2\)：
  • 如果它是无符号数，则表示十进制的 7。
  • 如果它是四位补码数，仍然表示 7。
• 但对于 \(1011_2\)，情况就不同了：
  • 如果它是无符号数，则表示 11；
  • 如果它是补码数，则表示 -5。

补码数的还原：

• 当最高位为 1 时，我们知道这是一个负数，因此需要通过还原补码来获得其对应的十进制负数。还原的过程包括：
  1. 减去 1：从补码数中减去 1。
  2. 取反：将每一位翻转。
• 例如，\(1011_2\) 是四位补码数：
  • 首先减去 1 得到 \(1010_2\)；
  • 然后取反，得到 \(0101_2\)，即 5。因此，\(1011_2\) 对应的十进制值是 -5。

练习示例：

• 例如，给定一个四位补码数 \(1100_2\)，将其转换为十进制：
  1. 识别符号位：最高位为 1，表示负数。
  2. 还原补码：
     • 首先减去 1，得到 \(1011_2\)；
     • 然后取反，得到 \(0100_2\)，即 4。因此，\(1100_2\) 对应的十进制值是 -4。

二进制补码运算与小数表示

小数在二进制中的表示：

• 小数在二进制中使用类似于科学计数法的表示形式，称为浮点数表示。浮点数的表示由以下几个部分组成：
  • 尾数（mantissa）：表示数值部分，通常是一个带符号的整数。
  • 指数（exponent）：表示浮点数的倍数或缩放因子，也带符号。
  • 基数（base）：通常是 2 或 10，表示数的进制。
• 例如，十进制中的 0.1 可以表示为： \[ 1 \times 10^{-1} \]
  • 尾数为 1，指数为 -1，基数为 10。在二进制中，类似的表示法被用来处理小数。

为什么浮点数有效？：

• 浮点数的表示非常适合处理小数和非常大的或非常小的数。因为尾数和指数都是整数，而计算机已经能够高效处理带符号的整数，浮点数的计算可以通过现有的整数运算单元完成。
• 浮点数使得在二进制中表示小数变得可能，尤其是在科学计算、金融计算等需要处理大量小数运算的场景中。

逻辑运算与布尔代数

布尔代数的介绍：

• 计算机不仅处理数字，还处理逻辑值（True 和 False）。在二进制系统中，True 用 1 表示，False 用 0 表示。
• 三种基本的布尔运算包括：
  • 与（AND）：两个条件都为 True 时，结果为 True。
  • 或（OR）：任一条件为 True 时，结果为 True。
  • 非（NOT）：对条件取反，True 变 False，False 变 True。

布尔运算的真值表：

• 与运算：只有当两个输入都为 1 时，结果为 1；否则为 0。
• 或运算：当任一输入为 1 时，结果为 1；如果两个输入都为 0，结果为 0。
• 非运算：将输入的值翻转，0 变 1，1 变 0。

计算机中的布尔逻辑

布尔逻辑在计算机中的作用：

• 计算机使用布尔逻辑来进行决策和控制流。例如，程序中的条件判断语句（如 if 语句）依赖于布尔逻辑来确定接下来要执行的代码。
• 逻辑门（如 AND、OR、NOT 门）是计算机硬件中基本的电路单元，通过组合这些门可以实现复杂的逻辑和运算。

布尔运算与二进制的结合：

• 通过将布尔逻辑与二进制数字相结合，计算机可以进行复杂的算术运算、逻辑判断和数据操作。这些运算是所有现代计算机处理数据的基础。

布尔运算基础：

• 逻辑与（AND）：当两个输入值都为 True 时，结果为 True；其他情况下，结果为 False。

  • 真值表：

    

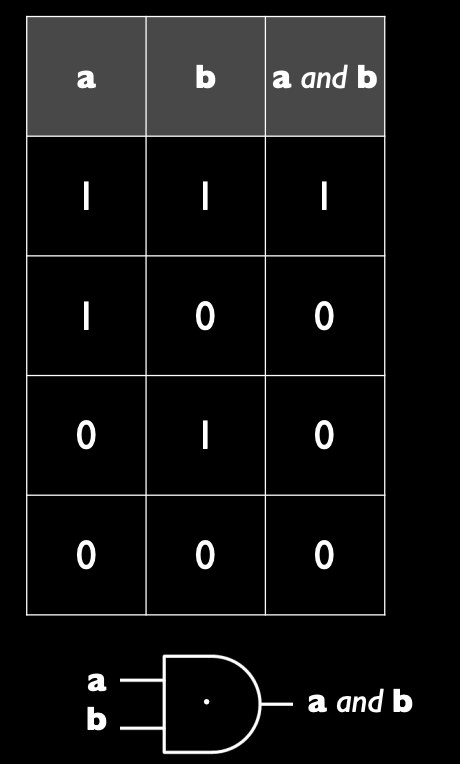
  • 例如，当 (A = 1) 且 (B = 1) 时，逻辑与结果为 (1)。

• 逻辑或（OR）：只要有一个输入为 True，结果为 True；如果两个输入都为 False，结果为 False。

  • 真值表：

    

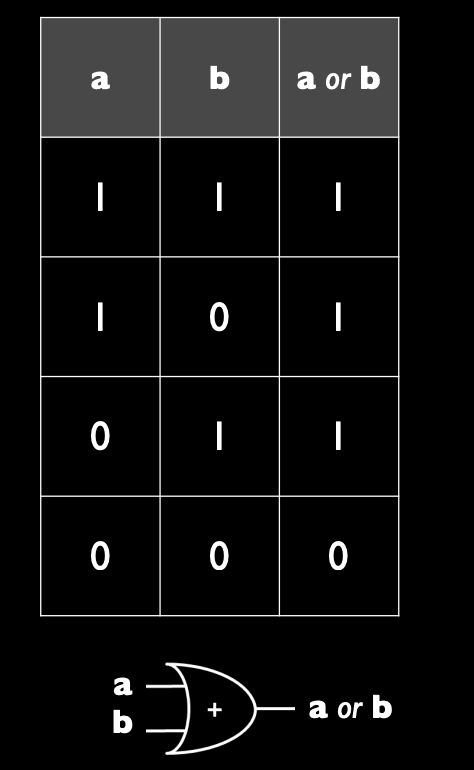
• 逻辑非（NOT）：只有一个输入，结果是输入的相反值。

  • 真值表：

    

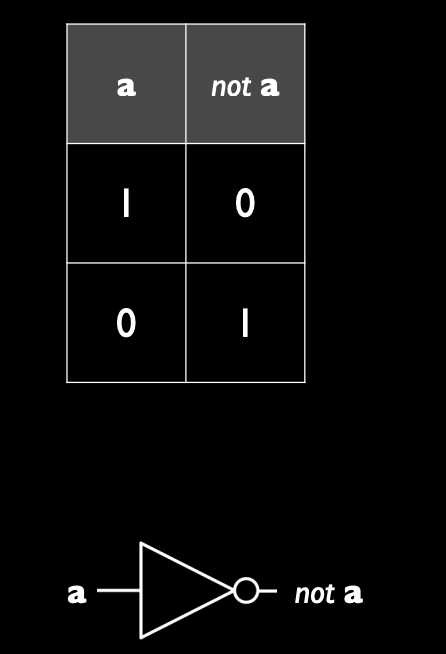
布尔运算是一种简单的计算形式，输入是布尔变量（True/False 或 0/1），输出也是布尔变量。这些运算构成了计算机处理逻辑判断的基础。

逻辑与、或、非可以组合形成复杂的逻辑电路，并且是构建现代计算机的核心元素。

逻辑门：

• 布尔运算的物理实现通过逻辑门来完成。每个逻辑门都有特定的符号和功能：
  • 与门（AND Gate）：表示逻辑与操作，符号为一个带有“·”的 D 形图。
  • 或门（OR Gate）：表示逻辑或操作，符号为一个带有“+”的弯曲 D 形图。
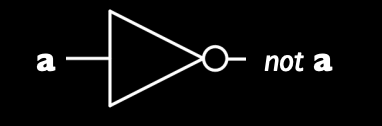
  • 非门（NOT Gate）：表示逻辑非操作，符号为一个带小圆点的三角形。

逻辑门的工作原理：

• 与门、或门和非门各自执行与、或、非运算，输入是 0 或 1（False 或 True），输出也是 0 或 1。
• 这些逻辑门是现代计算机的基础组件，通过组合它们可以构建复杂的计算系统。

构建现代计算机的基础

从逻辑门到计算机：

• 通过组合与、或、非门，可以实现所有的布尔运算，并且能够构建更复杂的逻辑电路，例如加法器、乘法器等，这些电路可以执行基本的算术运算。
• 例如，全加器电路（Full Adder）可以使用逻辑门来实现二进制数的加法，它是计算机进行算术运算的基础之一。

为什么只需要这三种操作？：

• 虽然逻辑与、或、非运算看起来非常简单，但它们已经足够强大，能够表达所有的布尔逻辑。
• 通过组合这些基本操作，可以实现任意复杂的运算，构建完整的计算系统。
• 冯·诺依曼架构的计算机正是基于这些逻辑运算来实现计算的。

物理实现：从逻辑门到晶体管

逻辑门的物理实现：

• 逻辑门的底层实现通常通过晶体管完成。晶体管可以用来构建与、或、非门，从而实现逻辑运算。
• 晶体管通过控制电流的通过与否来模拟 0 和 1 的状态。例如，两个晶体管可以串联组成与门，只有当两个晶体管都导通时，电流才能通过，表示结果为 1。

计算机的核心逻辑：

• 通过数十亿个晶体管的组合，现代计算机能够执行非常复杂的计算。虽然底层运算依赖于简单的逻辑与、或、非，但这些运算的组合能够实现所有的计算任务。

晶体管的基本概念：

• 晶体管是现代计算机的基础，用于控制电流的通过与否，模拟二进制状态：0 表示无电流（开关断开），1 表示有电流（开关闭合）。
• 我们可以使用晶体管构建逻辑门，这些逻辑门执行布尔运算，如与（AND）、或（OR）、非（NOT）。

构建 AND 门：

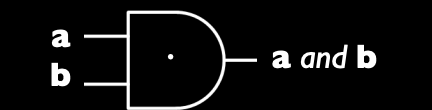
• 逻辑与（AND）运算：只有当两个输入都为 1 时，输出才为 1，否则输出为 0。

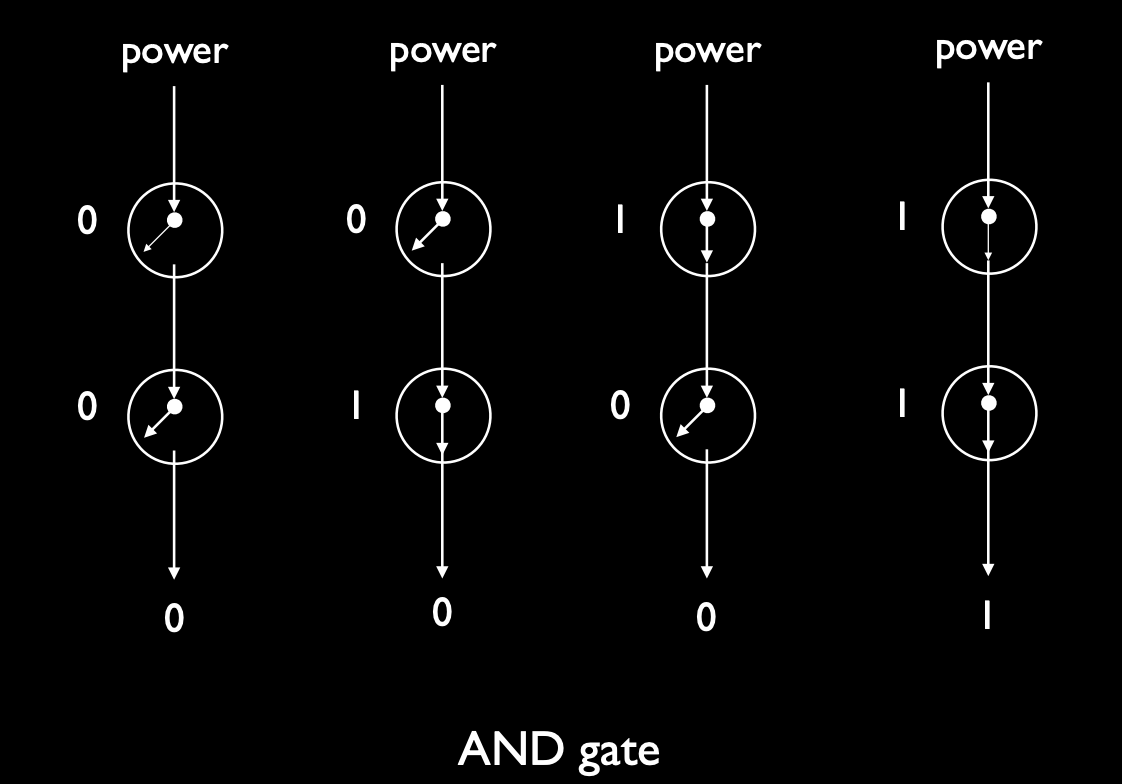
• 通过将两个晶体管串联（即将一个晶体管的输出连接到下一个晶体管的输入），可以实现 AND 门：
  • 当两个输入 \(A\) 和 \(B\) 都为 1 时，电流能够从顶部流到底部，输出为 1。
  • 如果任一晶体管处于关闭状态（输入为 0），电流被阻断，输出为 0。

• 串联结构表示只有在两个输入都为 1 时电流才能通过。

  

构建 OR 门：

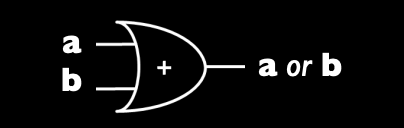
• 逻辑或（OR）运算：只要有一个输入为 1，输出就为 1。

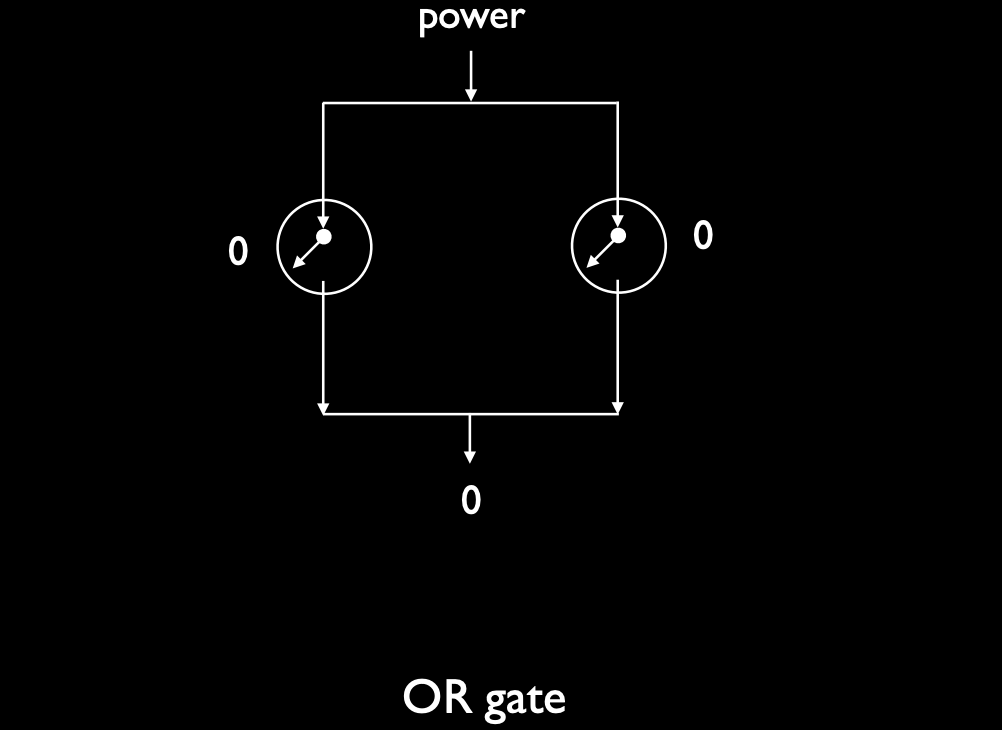
• OR 门的晶体管配置为并联，而不是串联：
  • 并联意味着只要任一晶体管允许电流通过（输入为 1），输出就为 1。
  • 当两个输入都为 0 时，电流无法通过，输出为 0。

• 并联结构确保只要有一个输入为 1，电流就能通过并输出 1。

  

构建 NOT 门：

• 逻辑非（NOT）运算：将输入的布尔值取反，即输入为 0 时输出为 1，输入为 1 时输出为 0。

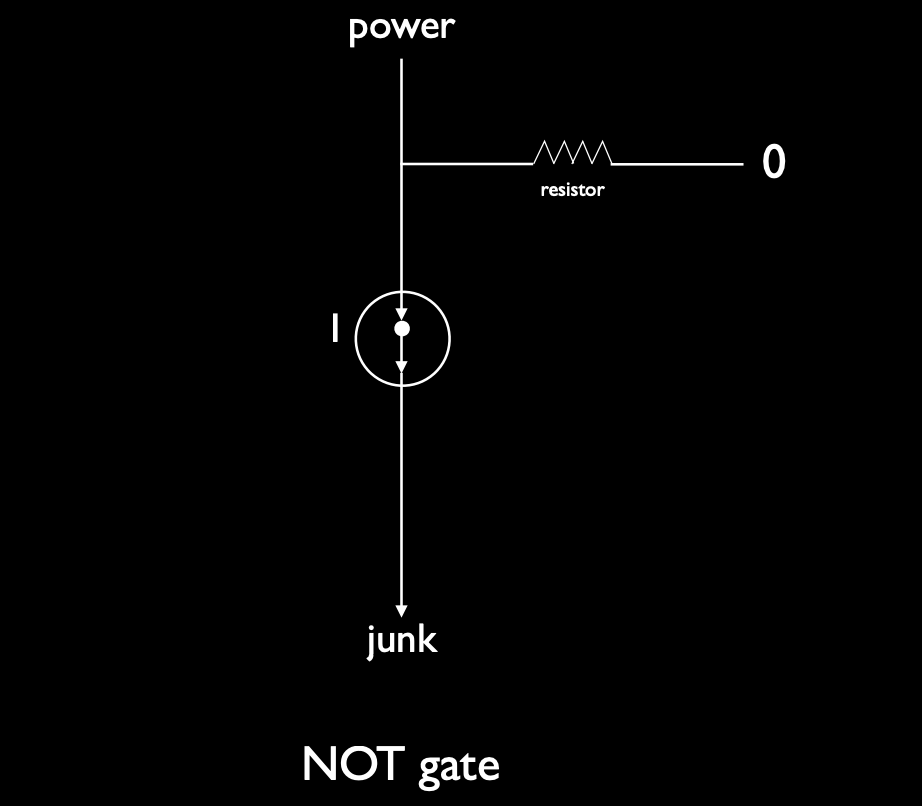
• NOT 门的设计仅需要一个晶体管：

  • 当输入为 0 时，晶体管关闭，电流通过并输出 1。
  • 当输入为 1 时，晶体管打开，电流被阻断，输出 0。

  

逻辑门的组合与计算

逻辑门的组合：

• 通过将 AND、OR、NOT 门组合，可以构建更复杂的逻辑电路。这些电路能够实现诸如加法、乘法等更复杂的运算。
• 例如，两个 AND 门和一个 OR 门的组合可以构建一个半加器（用于二进制加法）。
• 通过将多个逻辑门组合，可以构建出复杂电路。计算机的所有复杂运算都源自这些基本逻辑门的组合。

构建复杂计算：

• 通过组合这些基本的逻辑门，计算机能够执行二进制运算、比较操作和条件判断等。
• 计算的核心在于通过晶体管构建的逻辑门能够处理任意的布尔运算，进而实现二进制数的加法、减法、乘法和除法。

晶体管的规模化与计算能力：

• 晶体管是现代计算机中最小的计算单元，通过控制电流的流动，实现二进制的逻辑操作。
• 随着技术进步，晶体管的尺寸越来越小。现代计算机能在一个微小的芯片中集成数十亿个晶体管，从而实现巨大的计算能力。
• 晶体管的微缩和高密度排列使得我们能在像手机这样的设备中进行复杂的计算任务。