Lecture 12. Trees

Announcements

Cats 项目：Cats 项目截止日期为下周五，但为了确保你按时完成，你需要在下周二前完成第一阶段，并获得检查点。如果你提前完成第一阶段，可以随时提交已完成的部分来获得该部分的分数。另外，如果你在下周四之前提交整个项目，可以获得一个额外的加分点。
- 阶段划分：
  - 第一阶段：测量打字速度并选择打字内容。
  - 第二阶段：构建自动纠错系统。
  - 第三阶段：构建多人游戏模式。
- 你可以提前在 cats.cs61a.org 上体验多人模式，系统会为你匹配其他正在尝试进行多人游戏的玩家。
考试准备：我们将在本周五下午 2:00 举行考试准备会议。此外，还有额外的问答环节，你可以在这里查看所有录音。
Hog 策略比赛：Hog 策略比赛结束了，恭喜所有参与者！这次比赛有超过 150 次提交，最后出现了五名并列第一的选手，分别是 Bobby Tables、匿名诗人、黄金比例、Wet App Program 和 Blockchain。每位并列第一的选手都表现出色，没有人能完全击败对方。

今天的内容：Trees 树

今天的主题是树（Trees），树是一种递归的数据结构，广泛应用于网站、组织架构、政府系统等具有层次结构的表示中。树结构是我们之前学习的容器和递归结合的体现，它能够帮助我们处理更复杂的数据层次。

闭包性质是树结构的核心。它指的是通过某种方法组合的数据，可以继续使用相同的方法组合。例如，列表可以包含其他列表作为元素，这种特性使得我们能够构建层次化的数据结构。在表示这些结构时，我们需要使用方框和指针（Box and Pointer）记法，帮助我们追踪哪些数据包含在另一个数据中。

Box and Pointer 记法：这种记法用于在环境图中表示列表。当列表包含多个元素时，我们会用相邻的方框表示每个元素，并用指针指向其中的复合值。

列表示例

例如，假设我们有一个列表 pair = [1, 2]，我们可以在环境图中用两个相邻的方框来表示列表的两个元素，并给每个方框标上索引。

pair = [1, 2]

环境图中的表示方式将如下：

pair 绑定到一个包含两个元素 1 和 2 的列表。
每个元素的索引（从 0 开始）标记在对应的方框上。

通过树结构和递归，我们可以处理更加复杂的数据和逻辑，未来会在更多实际应用中看到树结构的重要性。

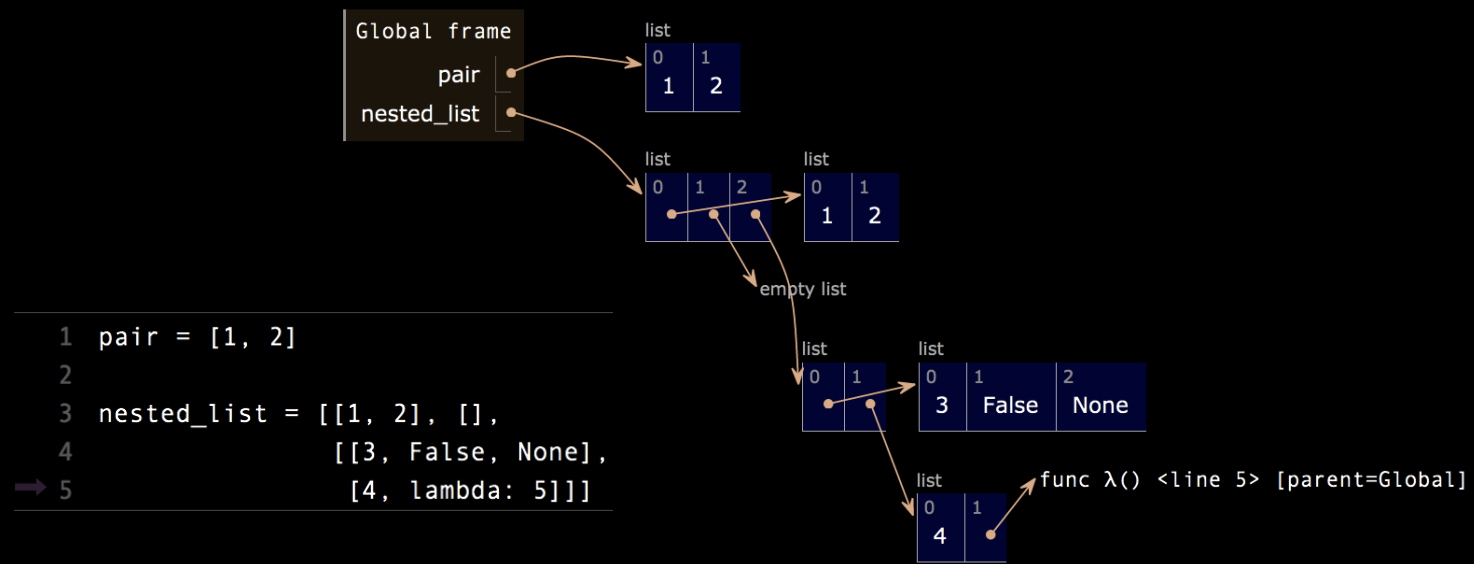
复杂列表的表示

当我们创建一个包含其他列表的嵌套列表时，比如 nested_list = [[1, 2], [], [[3, False, None], func]]，这会生成一个层次化结构。在“方框和指针”记法中，每个列表会指向其他列表（或是其他复合值），形成一个包含多个部分的树形结构。每个原始值（如整数、布尔值等）会直接显示在方框中，而每个函数或复杂值则会以箭头指向它们的具体表示。

Slicing 切片

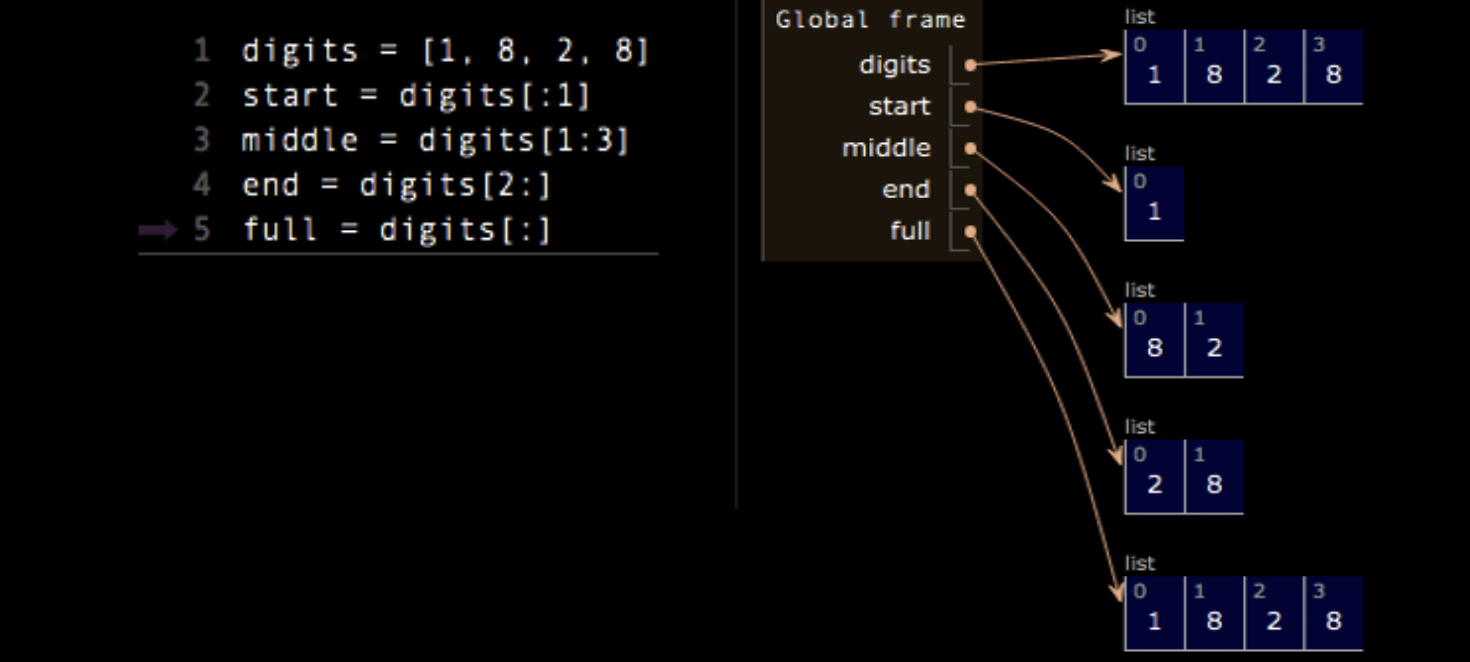
接下来，我们讨论了如何使用切片操作符来获取列表的子集。比如，假设我们有一个列表 odds = [3, 5, 7, 9, 11]，我们可以通过切片 odds[1:3] 来获取 [5, 7]。Python 的切片操作符的语法如下：

list[start:end]

start: 切片开始的索引（包含）。
end: 切片结束的索引（不包含）。

例如，odds[1:3] 返回索引 1 和 2 的元素，但不包括索引 3。

如果我们省略 start，它会从列表的开头开始切片，例如 odds[:3] 返回 [3, 5, 7]。
如果省略 end，它会一直切到列表的结尾，例如 odds[1:] 返回 [5, 7, 9, 11]。
odds[:] 返回整个列表 [3, 5, 7, 9, 11]。

切片操作每次都会生成新的列表，这意味着原始列表不会被修改。

序列聚合

在处理列表、字典等容器类型时，常常需要对其中的元素进行聚合操作。Python 内置了一些用于序列聚合的函数，使得这些操作更加高效。一个常见的例子是 sum() 函数，它可以对一个可迭代对象的元素求和：

sum(iterable, start=0)

iterable: 需要求和的序列。
start: 起始值，默认为 0，但可以设置为其他类型的值。

例如：

sum([2, 3, 4])  # 返回 9

如果我们想要对非数字元素（比如列表）进行操作，可以通过提供合适的起始值。例如：

sum([[2, 3], [4]], start=[])  # 返回 [2, 3, 4]

这会将 [2, 3] 和 [4] 合并成一个列表 [2, 3, 4]。如果不提供 start 值，程序会报错，因为默认的起始值是 0，而 0 不能与列表相加。

树的基本概念

我们现在进入了一个新的主题——树（Tree），这是一种非常重要的数据抽象，用于表示层级关系。在计算机科学中，树通常“倒着生长”，即树的根部在顶部，叶子在底部。下面我们将讨论树的常见术语和结构。

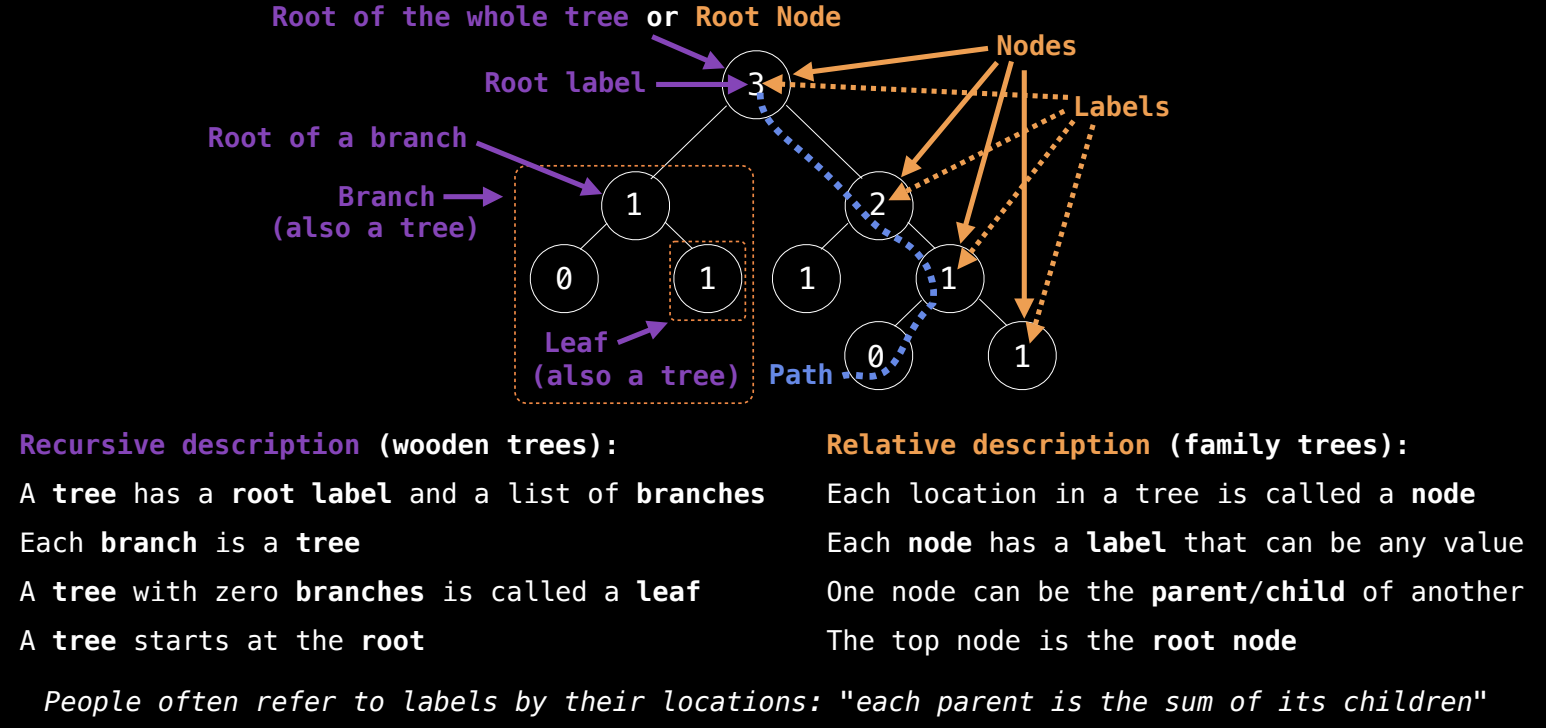
树的常见描述有两种：一种是递归描述，一种是家庭树的描述。

递归描述：树由一个根节点（root label）和一系列分支（branches）组成。每个分支本身又是一棵树。这意味着，树的每个分支也有自己的根节点和可能的分支。如果一个树没有分支，我们称之为叶子（leaf）。因此，树的结构是递归的，可以通过树的根节点和分支来定义。
家庭树描述：树中的每个位置被称为节点（node）。根节点是位于树顶部的节点，而每个节点都有一个标签，标签可以存储任何值。通过这种方式，我们可以将树描述为一个层次结构，其中一个节点可以是另一个节点的父节点（parent）或子节点（child）。我们还可以描述祖先、后代和兄弟姐妹等关系。

树的实现

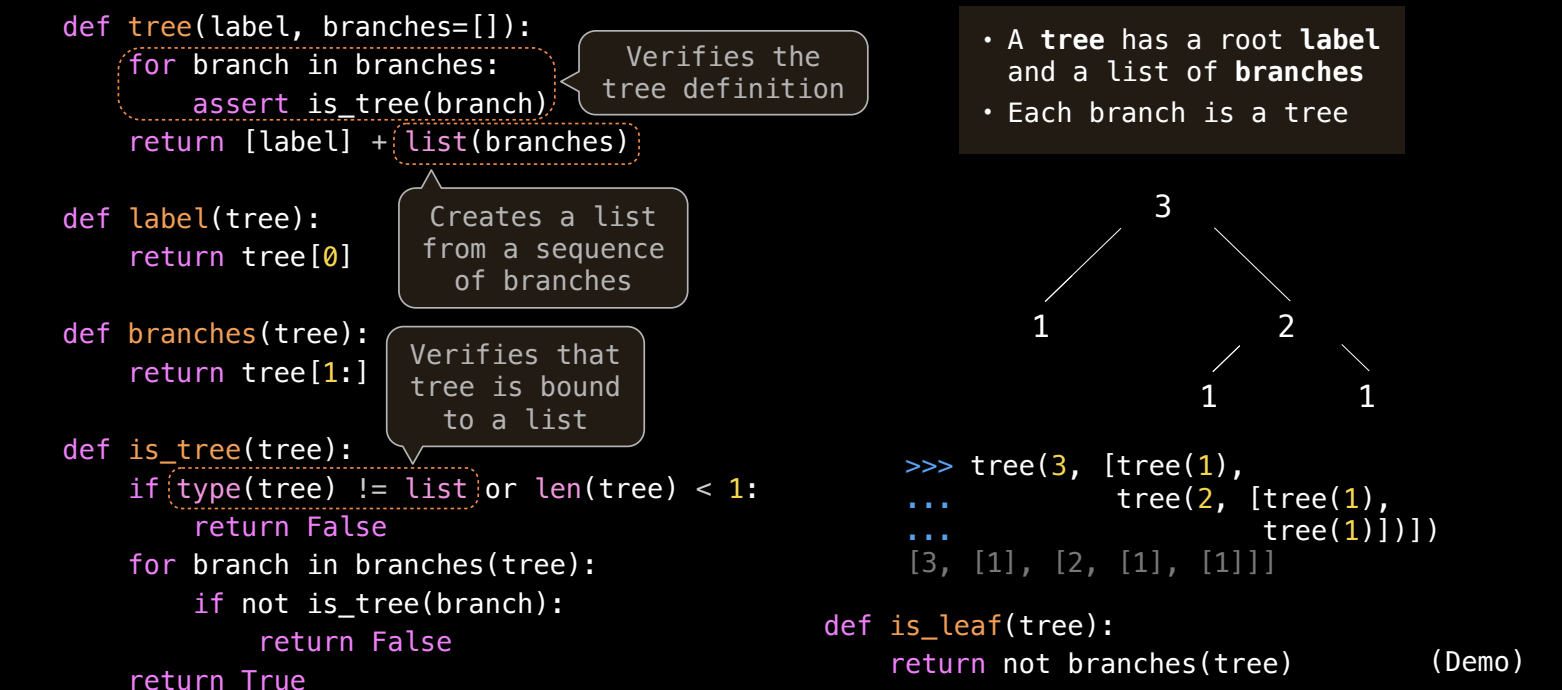
def tree(label, branches=[]):
    for branch in branches:
        assert is_tree(branch)  # 验证是否是合法的树
    return [label] + list(branches)

def label(tree):
    return tree[0]

def branches(tree):
    return tree[1:]

def is_tree(tree):
    if type(tree) != list or len(tree) < 1:
        return False
    for branch in branches(tree):
        if not is_tree(branch):
            return False
    return True

def is_leaf(tree):
    return not branches(tree)

一个树由标签 (label) 和一组分支 (branches) 组成，其中每个分支本身也是一棵树。这种定义可以递归地表示复杂的嵌套结构。

def tree(label, branches=[]):
    return [label] + branches

label：树的根节点。
branches：一个列表，表示该树的子树集合。

访问函数

要操作树的各个部分，可以定义两个访问函数：

label(tree)：返回树的根节点（标签）。
```
def label(tree):
    return tree[0]
```

branches(tree)：返回树的分支。

def branches(tree):
    return tree[1:]

示例

>>> tree(3, [tree(1), tree(2, [tree(1), tree(1)])])
[3, [1], [2, [1], [1]]]

在这个例子中，树的结构可以表示为一个根节点为 3 的树，它有两个子树，分别是根节点为 1 和根节点为 2 的树，而根节点为 2 的树本身还有两个子树，根节点都为 1。

验证树的合法性

为了确保每个分支都是一棵有效的树，我们可以定义一个辅助函数 is_tree(tree)，用于验证输入是否符合树的定义。

def is_tree(tree):
    if type(tree) != list or len(tree) < 1:
        return False
    for branch in branches(tree):
        if not is_tree(branch):
            return False
    return True

type(tree) != list：树的基本结构应该是列表。
len(tree) < 1：树至少需要包含一个标签。
递归检查：对于每个分支，递归地检查它是否也是一棵树。

判断叶节点

叶节点是没有子树的节点，我们可以通过检查分支是否为空来判断某个节点是否为叶节点。

def is_leaf(tree):
    return not branches(tree)

如果 branches(tree) 为空，说明该树没有子树，因此它是一个叶节点。

树的结构解析

在这个树的实现中，树被表示为一个列表，列表的第一个元素是树的标签（根节点），其余的元素是树的分支（子树）。每个分支本身又是一个树的列表，递归地重复这一结构。

创建树：通过 tree() 函数来创建树对象，同时确保所有分支都是合法的树。
访问树：通过 label() 函数访问根节点，通过 branches() 函数获取所有子树。
验证树：is_tree() 函数递归验证树的结构是否正确。
判断叶节点：is_leaf() 函数用于判断某个节点是否为叶节点。

树结构的例子

考虑如下的树结构：

可以通过以下代码生成：

>>> t = tree(3, [tree(1), tree(2, [tree(1), tree(1)])])
>>> print(t)
[3, [1], [2, [1], [1]]]

树的构造与递归处理

我们可以通过递归构造树，也可以递归地处理树。例如，下面是一个构造 Fibonacci 树的递归函数 fib_tree：

Fibonacci 树的递归构造

Fibonacci 树是用递归方式生成的树，每个节点的值等于两个子节点的值之和。叶节点代表 Fibonacci 数列中的基本值 F(0) 或 F(1)。下面是 Fibonacci 树的构造函数：

def fib_tree(n):
    """构造一个表示 Fibonacci 数列的树，根节点为 Fibonacci(n) 的值。"""
    if n <= 1:
        return tree(n)  # 基本情况：Fibonacci(0) 或 Fibonacci(1) 都是叶子
    else:
        left = fib_tree(n - 2)
        right = fib_tree(n - 1)
        return tree(label(left) + label(right), [left, right])  # 递归构造树

当 n <= 1 时，我们创建一个叶子节点，表示 Fibonacci 序列的基本值。
否则，我们递归构造左分支和右分支，分别代表 Fibonacci(n-2) 和 Fibonacci(n-1)。
最后，通过根节点值 label(left) + label(right) 和分支列表 [left, right] 构建一个新的树。

树的递归处理

在树的处理过程中，递归是常用的解决方法，尤其是在处理树的叶节点时，叶节点常常作为递归的基准情况（base case）。递归的核心思路是在每个分支上递归调用函数，最终将结果汇总。

1. 叶子计数

我们可以写一个递归函数来统计树中的叶子节点数：

def count_leaves(t):
    """统计树 t 中的叶子节点数。"""
    if is_leaf(t):
        return 1  # 如果是叶子节点，返回 1
    else:
        branch_counts = [count_leaves(b) for b in branches(t)]  # 递归统计每个分支中的叶子节点
        return sum(branch_counts)  

基准情况：if is_leaf(t) 用来检查当前节点是否为叶节点，如果是，则直接返回 1，表示这个节点是一个叶节点。
递归情况：branch_counts = [count_leaves(b) for b in branches(t)] 遍历当前树的所有分支，对每个分支递归调用 count_leaves，将每个分支的叶节点数量记录下来。最终通过 sum(branch_counts) 汇总所有分支的叶节点数。

2. 收集叶子标签

我们还可以编写一个函数，用来获取树中所有叶子节点的标签。这类似于叶子计数，但需要返回所有叶子的标签，而不仅仅是数量。为了实现这一点，我们可以递归收集每个分支中的叶子标签，并将它们合并成一个列表。

实现收集叶子标签的代码：

def leaves(t):
    """返回树 t 中所有叶子的标签列表。"""
    if is_leaf(t):  # 基本情况：如果 t 是叶子，返回标签列表
        return [label(t)]
    else:
        # 递归情况：对每个分支递归调用 leaves，并使用 sum 合并结果
        return sum([leaves(b) for b in branches(t)], [])

基准情况：如果当前节点是叶节点，直接返回包含该节点标签的列表 [label(tree)]。
递归情况：如果当前节点有分支，则对每个分支调用 leaves(b)，递归收集每个分支的叶节点，并使用 sum() 将所有分支的叶节点列表合并成一个完整的列表。

sum 函数在这里用于展平列表，即将多个分支的结果合并成一个列表，而不是嵌套的列表。

示例

假设我们有 Fibonacci 树的实现，并对 fib_tree(5) 调用 leaves：

>>> leaves(fib_tree(5))
[1, 0, 1, 0, 1, 0, 1]

这将返回 Fibonacci 树中的所有叶节点，按顺序列出。

3. 生成新树（递增叶子节点）

我们还可以编写一个函数，用来生成一棵新的树，要求新树的叶子节点的标签值增加。例如，我们可以写一个函数 increment_leaves，它会递归地处理树中的叶子节点，并生成一个叶子标签值增加的新树。

实现递增叶子标签的代码：

def increment_leaves(t):
    """返回树 t，但叶子节点的标签值增加 1。"""
    if is_leaf(t):
        return tree(label(t) + 1)  # 如果是叶节点，则将标签加 1
    else:
        bs = [increment_leaves(b) for b in branches(t)]  # 对每个分支递归调用
        return tree(label(t), bs)  # 返回标签不变的根节点与递归后的分支

基准情况：如果当前节点是叶节点，直接将其标签加 1，返回新的叶节点树。
递归情况：如果当前节点有子树（即非叶节点），则递归地对每个子树调用 increment_leaves，并将其组合为新的树返回。

4. 递归处理所有节点

有时我们可能希望处理树中的每个节点，而不仅仅是叶子节点。例如，编写一个递归函数 increment_t，它会递增树中所有节点的标签。这里我们不需要单独处理叶子节点，而是对所有节点统一处理。

实现递增所有节点标签的代码：

def increment_t(t):
    """返回树 t，但所有节点的标签值增加 1。"""
    # 返回一个新树，其中根节点的标签值加 1，所有分支也递归调用 increment_t
    return tree(label(t) + 1, [increment_t(b) for b in branches(t)])

递归处理所有节点：这里没有显式的基本情况，因为递归终止自然发生在分支为空时。
不管当前节点是否为叶节点，都将其标签加 1，并对所有分支递归调用 increment。

5. 打印树结构

最后，我们可以编写一个函数，用来打印树的结构，方便我们查看树的布局。这个函数可以递归地打印每个节点的标签，并递归调用分支来打印子树。

实现树结构打印的代码：

def print_tree(t, indent=0):
    """打印树 t 的结构，缩进表示层级。"""
    print('  ' * indent + str(label(t)))  # 打印根节点标签
    for b in branches(t):
        print_tree(b, indent + 1)  # 递归打印子树

缩进打印：indent 参数用于控制缩进，表示树的层级结构。
递归打印：对每个分支调用 print_tree，逐层打印树的结构。

打印路径和标签求和

这部分我们将实现一个递归函数，处理树的叶子节点，沿着从根到叶子的路径累加标签值，并打印出每条路径的标签和。我们也会探讨递归过程中传递参数和构造结果的两种不同策略。

1. 递归构建树的路径和

我们的目标是：给定一棵树，对于每个叶子节点，计算从根到该叶子节点的标签和，并将该和打印出来。为了实现这个功能，我们需要递归遍历树，并在遍历过程中将路径上的标签累加。

实现思路：

递归过程中，我们不仅需要知道当前节点的标签，还需要记录从根节点到当前节点为止的累积和。这样，当递归到达叶子节点时，我们就能够输出这条路径的标签和。
为了做到这一点，我们可以在递归函数中添加一个额外的参数，记录当前累积的标签和。随着递归深入，这个累积和逐步增加，直到我们到达叶子节点并打印它。

2. 树的路径和递归函数

下面是实现该递归函数的代码：

def print_sums(t, so_far):
    """递归遍历树 t，打印从根到叶子的标签和。"""
    # 更新当前路径的累积和
    so_far += label(t)
    
    # 基本情况：如果是叶子节点，打印累积的标签和
    if is_leaf(t):
        print(so_far)
    else:
        # 递归处理每个分支
        for b in branches(t):
            print_sums(b, so_far)

代码解释：

累积和的更新：在每次递归调用中，都会将当前节点的标签 label(t) 添加到累积和 so_far 上。
基本情况：如果当前节点是叶子节点，则打印累积和。叶子节点的判断通过 is_leaf(t) 实现。
递归处理：如果当前节点不是叶子节点，则递归处理它的每个分支，并将更新后的 so_far 传递给下一层递归。

3. 样例树的构建

让我们定义一棵数字树，并调用 print_sums 函数：

# 树的构建函数，树的表示形式为列表
def tree(label, branches=[]):
    return [label] + list(branches)

def label(tree):
    return tree[0]

def branches(tree):
    return tree[1:]

def is_leaf(tree):
    return not branches(tree)

# 构建样例树
numbers = tree(3, [tree(4), tree(5, [tree(6)])])

# 打印路径和
print_sums(numbers, 0)

这棵树的结构是：

从根 3 到叶子 4 的路径和为 3 + 4 = 7。
从根 3 到叶子 6 的路径和为 3 + 5 + 6 = 14。

输出结果应该是：

7
14

4. 处理字符树

我们还可以处理包含字符串标签的树。例如，构建一个字母树并打印从根到叶子的标签串：

# 构建字符树
haste = tree('H', [tree('A', [tree('S'), tree('T')]), tree('E')])

# 打印从根到叶子的路径标签串
print_sums(haste, "")

这棵树的结构是：

    H
   / \
  A   E
 / \
S   T

输出结果应该是：

HAS
HAT
HE

在处理字符串时，so_far 是一个累积的字符串，每次递归时将当前节点的标签追加到 so_far 中。

5. 递归策略的比较

我们探讨了两种递归策略：

基于返回值的递归：像计算阶乘的递归函数那样，依赖于递归调用的返回值来逐步构建最终结果。在树的情况下，这种策略常用于返回处理后的树或叶子节点集合。
基于参数传递的递归：像 print_sums 这样的函数，通过将中间结果（如累积和或累积的标签串）作为参数传递给下一层递归。在到达递归的基本情况时，直接使用这个中间结果。

这两种策略在不同场景下都有用武之地，尤其是处理树等递归数据结构时，基于参数传递的递归方法非常高效且易于理解。

通过本次讨论，我们展示了如何递归处理树的结构，特别是如何计算从根到叶子的路径和，以及如何通过递归传递中间结果来简化代码。这种递归模式在复杂数据结构的处理中十分有用，并且可以帮助我们更好地理解递归的威力和灵活性。