Lecture 5. Environments

Announcements

期中考试一将在下周一（14号），晚上7:00到9:00（太平洋时间）进行。考试将采用网络形式，题型包括简答题和选择题，主要要求你完成一些简短函数的实现。考试内容涵盖《Composing Programs》1.1到1.6章节，排除牛顿法和装饰器相关部分。

考试采用视频监考，但并不会实时观看你考试的过程。你需要录制屏幕和你的头部，可以使用Zoom、Loom等软件，也可以用手机等设备录制。录制方法灵活，具体操作指南会在稍后提供。如果不希望录制，可以填写豁免申请表，最晚需要在下周四提交。录制的视频只用于学术诚信调查。

推荐使用Loom来录制，它将视频自动上传到云端，不占用本地存储。如果网络不稳定，可以选择本地录制，Zoom可以实现本地录制。若录制中途失败，请继续完成考试，录制并非最重要，提交答案是核心部分。

如果考试时间（晚上10点到早上7点之间）对你的时区不便，或者考试时间冲突，可以填写表格申请延迟考试。表格需在下周四前提交。

考试规则

考试资料：可以使用官方提供的两页PDF学习指南（包括今天的课程内容），自己创建的一张双面笔记，以及草稿纸。如果需要电子版笔记，必须使用Google Doc。
在线工具：可以使用cs61a.org、piazza、code.cs61a.org（解释器）和tutor.cs61a.org（Python环境图生成器）。这些工具在考试中都可以使用，但不允许使用其他电子文档或终端程序。
禁止事项：不能访问Google、Reddit、StackOverflow等外部资源，不能与其他学生、曾修过课程的人，甚至家人交流讨论。

考试的详细内容和评分标准已更新至课程大纲，总分300分，成绩划分标准固定。获得A+需要几乎完美的表现，但整个学期有约10分的额外加分机会。获得A的学生可以跳过每次考试中最难的题目，只要其余部分都正确。

本周五下午2:10有考试准备会，助教将分享答题策略和展示过去的考试题目。下周五还有实验和作业项目的提前提交截止日期。

项目 Hog 已经发布，第一阶段需要在下周二前完成并提交以获得检查点加分。周五将有1对1的非正式辅导会，学生可以预约与导师讨论任何问题。

最后，请填写第2周的匿名反馈调查，帮助我们改进课程安排。

Environments for Higher-Order Functions

高阶函数是能够接受其他函数作为参数，或返回函数作为结果，甚至同时具备这两种能力的函数。在Python中，环境图（environment diagrams）可以帮助我们理解高阶函数的工作原理。环境图的规则在处理普通函数和处理高阶函数时是相同的，唯一的区别是高阶函数会将函数作为参数传递或返回。

例如，我们定义一个名为 apply_twice 的高阶函数，该函数接受另一个函数 f 和一个参数 x，然后将 f 应用于 x 两次，计算 f(f(x)) 的值。这个高阶函数的实现如下：

def apply_twice(f, x):
    return f(f(x))

我们可以传入一个平方函数 square，然后对数字3应用 apply_twice：

def square(x):
    return x * x

result = apply_twice(square, 3)
print(result)  # 输出 81

在这段代码中，apply_twice 函数将 square 函数应用于3，首先计算 square(3)，结果是9。然后再将 square 应用于9，得到 square(9) 的结果81。

环境图中的高阶函数

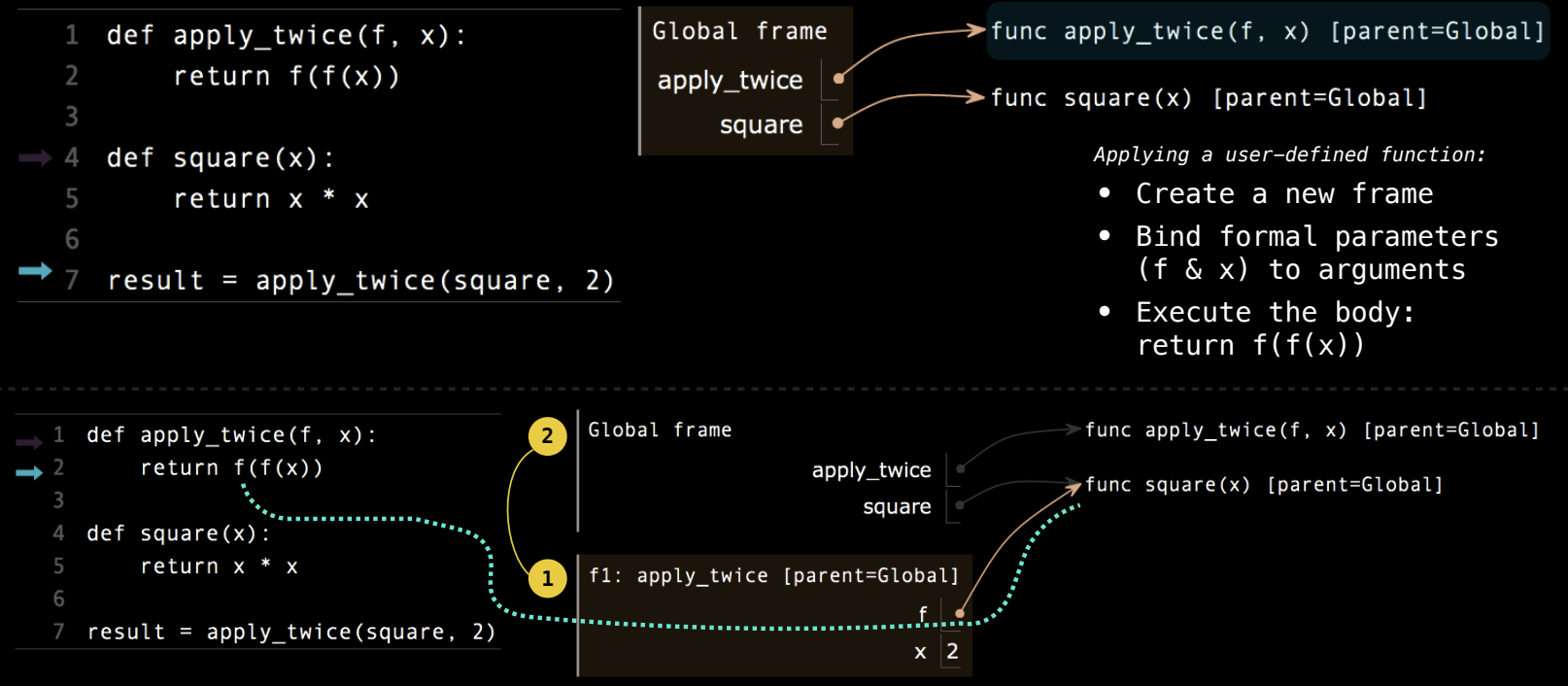
当我们在环境图中描述高阶函数的执行时，遵循和普通函数相同的规则：

定义阶段：首先定义 apply_twice 和 square 函数，这时并不会执行任何操作，仅仅是将名称与函数绑定。
调用阶段：调用 apply_twice(square, 3) 时，会为 apply_twice 创建一个新帧（frame），并将形式参数 f 和 x 分别绑定到 square 函数和数字3。
执行函数：apply_twice 的主体是 f(f(x))。首先计算 f(x)，即 square(3)，结果是9。然后再次计算 f(9)，即 square(9)，得到81，最后返回该值。

这个过程可以通过环境图清晰地展示，在 apply_twice 调用时，新的环境帧记录了 f 和 x 的绑定关系，以及函数调用过程中的值传递。

高阶函数的进一步应用

我们可以通过另一个例子，展示如何使用 while 循环和高阶函数组合：

def repeat(f, x):
    while f(x) != x:
        x = f(x)
    return x

在这个例子中，repeat 函数接受一个函数 f 和一个初始值 x，不断调用 f(x) 直到结果不再变化为止。

假设我们定义一个函数 g，它执行加法和除法操作：

def g(y):
    return (y + 5) // 3

result = repeat(g, 5)
print(result)  # 输出 2

repeat(g, 5) 的计算过程如下：

首先调用 g(5)，结果是 (5 + 5) // 3 = 3。
接着调用 g(3)，结果是 (3 + 5) // 3 = 2。
最后调用 g(2)，由于结果仍然是2，因此循环结束，repeat 函数返回2。

关键概念

高阶函数：可以接受或返回其他函数的函数。例如 apply_twice 和 repeat。
环境图：展示了函数调用过程中如何创建和管理环境帧，记录了函数参数和返回值的绑定关系。
函数作为一等公民：在Python中，函数可以作为参数传递、返回值返回，甚至在函数内部定义，这为高阶函数的实现提供了灵活性。

高阶函数不仅简化了代码，避免了重复逻辑，还提升了代码的可重用性和扩展性。

嵌套定义的环境

高阶函数 `make_adder` 的执行过程

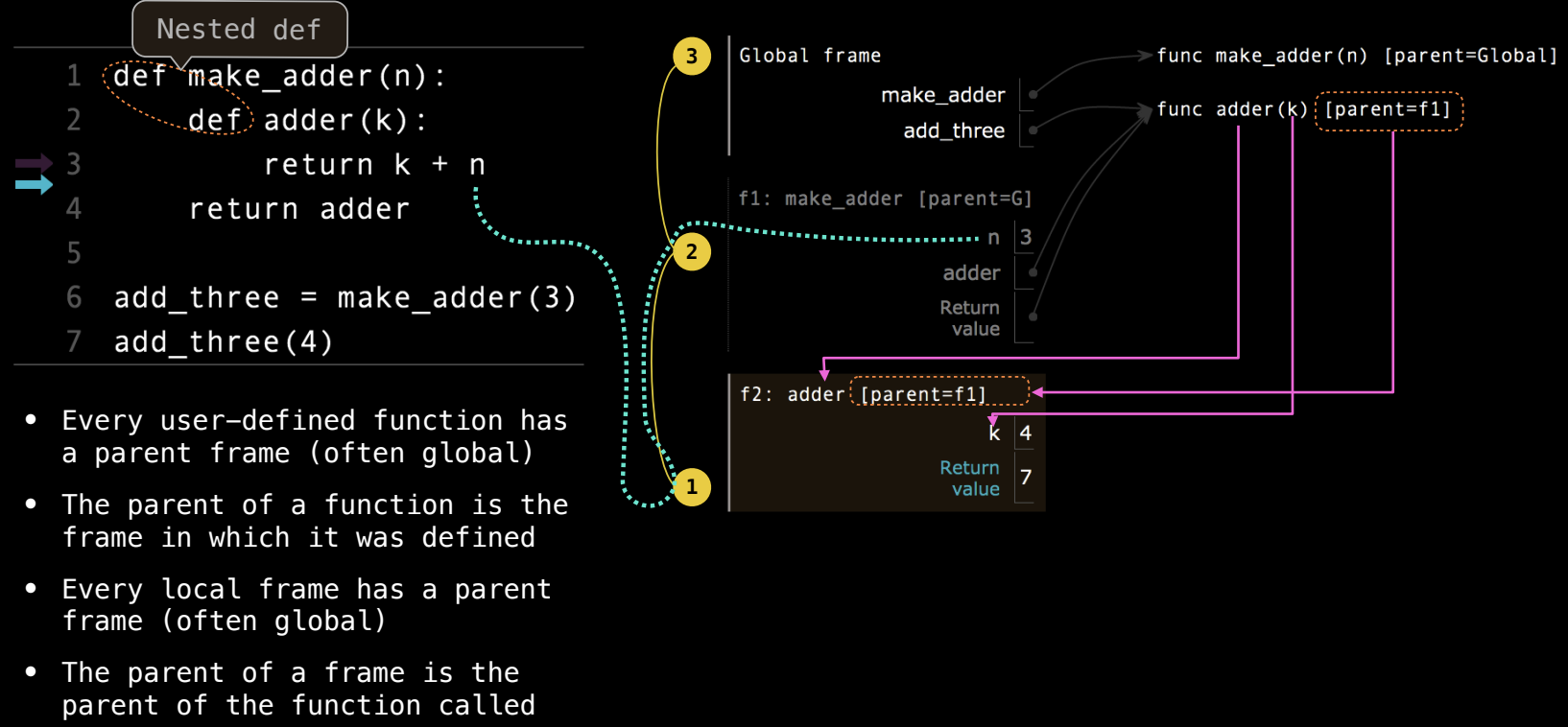
接下来，我们讨论了另一个高阶函数 make_adder 的环境图如何工作：

定义 make_adder 函数：
- 执行 def make_adder(n) 语句时，Python 创建了一个新的函数对象 make_adder。
定义和返回函数：

当调用 make_adder(3) 时，make_adder 函数被执行，创建一个新的帧（f1），其中 n 被绑定为 3。在 make_adder 函数体内定义了另一个函数 adder(k)，这个函数是闭包，它可以访问 make_adder 内部的变量 n。
adder(k) 函数被创建并绑定到 f1 帧。make_adder 函数返回 adder，这个函数被绑定到全局名称 add_three，所以现在 add_three 就是一个闭包，它“记住”了 n=3 的上下文信息。

调用返回的函数：

当调用 add_three(4) 时，会创建一个新的帧 f2，k 被绑定为 4。尽管 make_adder 函数早已执行完毕并返回，但由于 adder 是闭包，它依然可以访问 f1 中的 n=3。
在 adder 函数体内，表达式 k + n 被执行。首先在当前帧 f2 中查找 k，找到 k=4；然后在父帧 f1 中查找 n，找到 n=3。因此，k + n = 4 + 3 = 7，返回值为 7。

环境图的构建：

定义函数时：创建一个函数值，该函数的父环境为当前帧。例如，adder 的父帧是 f1，因为它是在 make_adder 的执行过程中定义的。
调用函数时：创建一个新的帧，用函数名称作为标题，并将形式参数绑定到实际的参数。函数帧的父环境是定义该函数时的帧，比如 adder 的父帧是 f1。
在函数体中查找变量时，首先在当前帧查找，如果找不到，则逐级向父帧查找，直到全局帧。

关键概念总结：

闭包（Closure）：函数可以“记住”其定义时的环境，函数返回后仍然能够访问那个环境中的变量。
父帧（Parent Frame）：每个函数都记录了其定义时的环境，调用函数时，新帧的父帧是函数定义时的帧，而不是调用时的帧。
环境查找链：变量查找时，首先在当前帧查找，如果没有找到，则向上查找父帧，直到找到为止。

高阶函数和环境图的结合揭示了如何通过函数的嵌套定义与作用域处理复杂的函数调用。让我们通过以下几个关键步骤来理解这些概念：

1. 局部变量和作用域：

在 Python 中，函数的形式参数和局部变量仅在该函数的局部作用域中可见。例如，f(x, y) 中的参数 x 和 y 只能在 f 的函数体内使用。当调用 g(a) 时，虽然 g 是在 f 中调用的，但 g 无法访问 f 的局部变量 y，这会导致错误。这是因为 g 的作用域中没有 y，而在查找变量时，Python 会先在当前函数的局部帧（local frame）查找，然后在全局帧（global frame）查找。如果两个函数独立定义（即没有嵌套），它们无法共享彼此的局部变量。

2. 嵌套函数和闭包：

相比之下，如果函数是在另一个函数内部定义的，例如 make_adder 中定义的 adder，则闭包允许内部函数访问外部函数的局部变量。通过环境图的构建，我们可以看到当 adder 被返回时，它仍然记住了 make_adder 的局部变量 n，从而实现了类似于“记忆”的效果。

例如，当 make_adder(2) 返回一个 adder 函数并将其绑定到 add_three，调用 add_three(4) 时，Python 会通过环境查找链找到 n=3（定义时的变量值），从而正确计算出 4 + 3 = 7。

3. 函数组合与高阶函数：

函数组合是一种强大的模式，它允许我们将多个函数组合成一个新函数。例如，compose1 函数接受两个函数 f 和 g，并返回一个新函数 h，这个 h 函数的执行顺序是先调用 g，然后将 g 的结果传递给 f。这种高阶函数的模式提供了极大的灵活性。

比如，squibble = compose1(square, triple) 会创建一个组合函数，调用 squibble(5) 时，首先计算 triple(5) 得到 15，然后再计算 square(15)，最终返回 225。通过环境图可以清晰地展示每一步的参数绑定、函数调用和返回值传递。

4. 环境图的具体构建：

环境图的构建步骤如下：

定义函数时：创建一个函数对象，并记录其定义时的父帧（通常是当前局部帧或全局帧）。例如，当在 make_adder 中定义 adder 时，adder 的父帧是 make_adder 的局部帧（f1）。
调用函数时：创建一个新的局部帧，将形式参数绑定到实际传入的参数，并将函数的父帧设置为调用时的帧。然后在新的局部帧中执行函数体，查找变量时遵循从局部帧到父帧的逐层查找机制。

5. 总结与要点：

局部作用域：每个函数都有自己的局部作用域，变量只能在定义它们的函数体内访问。
闭包和嵌套函数：内部函数可以通过闭包机制访问外部函数的局部变量，创建了灵活的函数状态管理方式。
函数组合和高阶函数：可以通过高阶函数将多个函数合成为一个，提升代码的可复用性和模块化。
环境图的重要性：环境图帮助我们跟踪函数调用过程中的变量绑定、作用域查找和返回值传递，从而深入理解复杂函数的执行流程。

通过这些要点和环境图的演示，我们能够更加清晰地理解 Python 中高阶函数及其背后的环境机制。

Local Names

内在函数名（Intrinsic Name）是指函数在定义时自动获得的名称，用于在调试或打印时识别函数。在使用 def 语句定义函数时，Python 会自动给函数一个内在函数名，而使用 lambda 表达式时，函数不会自动获得这样的名称。

我们可以通过对比 def 和 lambda 来更清楚地理解这个概念。

`def` 语句

def square(x):
    return x * x

在这个例子中，square 函数有一个明确的名称 “square”。如果你打印这个函数：

print(square)

你会看到输出类似于：

<function square at 0x7f8e9450e280>

其中，square 是函数的内在名称。

`lambda` 表达式

相比之下，使用 lambda 表达式创建的函数没有自动分配的名称。例如：

square = lambda x: x * x

如果你打印这个函数：

print(square)

输出会是：

<function <lambda> at 0x7f8e9450e310>

这里，<lambda> 表示这个函数是由 lambda 表达式创建的，但没有像 def 语句那样给出一个具体的名字。

关键区别

内在名称：使用 def 定义的函数会自动获得一个内在名称，而 lambda 表达式不会。lambda 函数的名字通常显示为 <lambda>。
环境图中的表现：当我们使用环境图（environment diagram）跟踪函数时，def 定义的函数会显示为其内在名称（例如 square），而 lambda 函数通常会显示为 <lambda>。

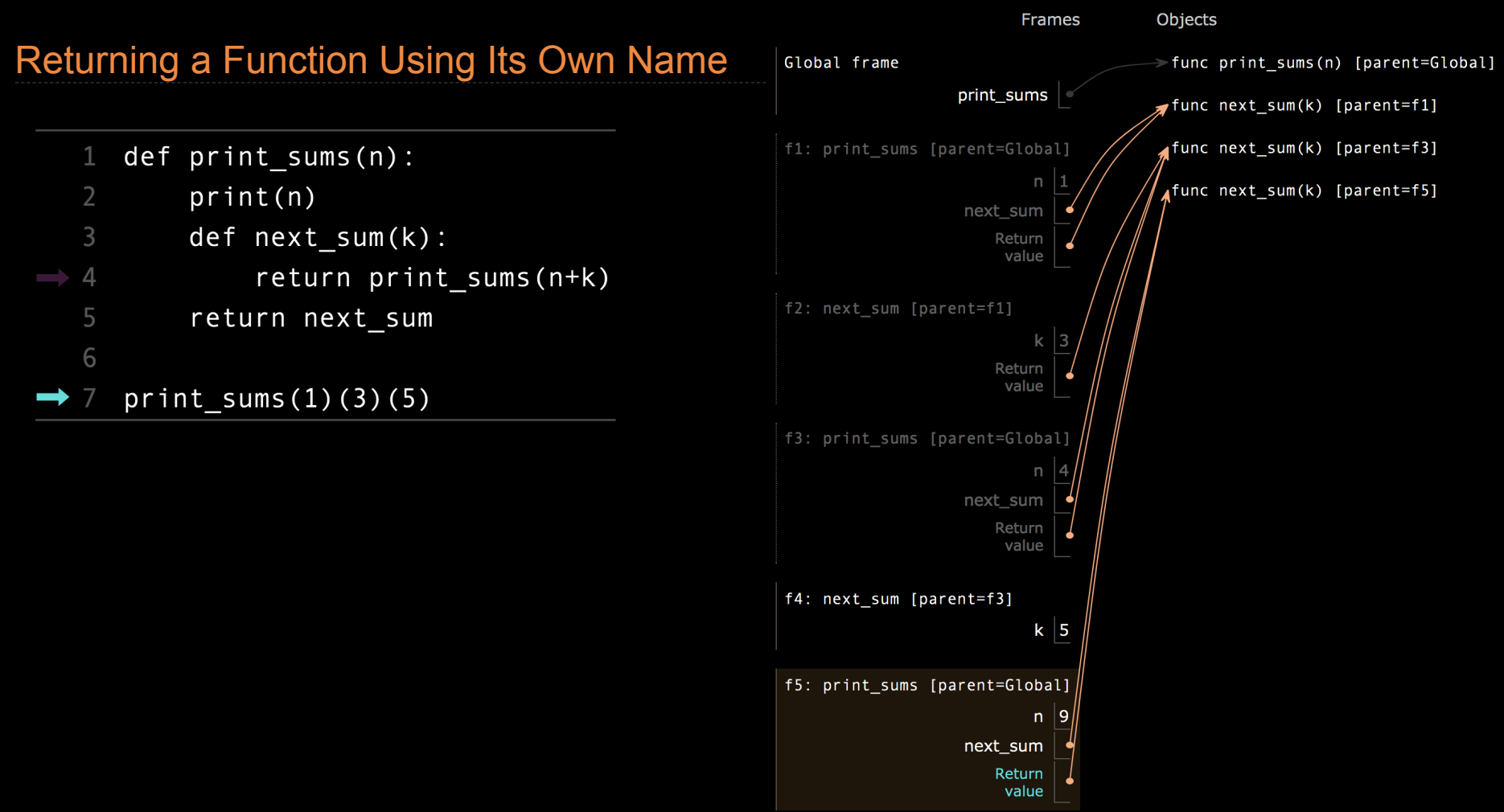
示例：递归函数 `print_sums`

在这个例子中，我们通过定义一个递归函数 print_sums 来实现逐步累加参数并打印结果的过程。以下是对这个过程的深入解析。

首先，print_sums 函数的主要作用是接收一个参数 x，打印当前的累加和，并返回一个新定义的函数 next_sum。next_sum 函数接收一个新的参数 y，然后将 x 和 y 相加，并再次调用 print_sums，实现递归调用。

过程解析

定义 print_sums：
- print_sums 函数被定义，等待调用。
- 这个函数的作用是打印当前的累加和，然后返回一个新函数 next_sum。
第一次调用 print_sums(1)：
- 在执行时，x 被绑定为 1。
- 函数打印当前累加和 1，然后返回函数 next_sum。此时，x = 1 被保存在返回的函数 next_sum 的环境中。
调用 next_sum(3)：
- next_sum 被调用，y 被赋值为 3。
- 由于 next_sum 是在 print_sums 函数内部定义的，它可以访问其父函数 print_sums 的环境变量。因此，next_sum 可以访问之前的 x = 1。
- 函数将 x + y 计算为 4，并将其传递给 print_sums 再次进行调用。
第二次调用 print_sums(4)：
- 新的 print_sums 调用中，x 现在是 4，这是前面步骤中 1 + 3 的结果。
- 函数打印当前累加和 4，然后返回一个新的 next_sum 函数，这个函数的环境中保存了 x = 4。
调用 next_sum(5)：
- next_sum 再次被调用，这次 y = 5。
- 由于环境的作用，next_sum 可以访问其父环境中的 x = 4。
- 函数计算 4 + 5 = 9，然后调用 print_sums(9)。
第三次调用 print_sums(9)：
- x 被绑定为 9，表示累加和为 1 + 3 + 5 = 9。
- 函数打印出 9，结束递归过程。

环境图解析

在每次调用时，print_sums 都会创建一个新的函数 next_sum，该函数捕获了当前的累加和 x。当 next_sum 被调用时，它可以访问它的父环境，从而能够获取之前累加的结果并进行进一步的累加。

这种设计利用了闭包（closure）的特性，即内部函数可以记住其定义时所在的环境，从而在后续调用中访问到当时的变量。这使得我们可以在每次调用 next_sum 时，累积之前的和。

通过递归地调用 print_sums 和返回 next_sum，我们实现了一个动态累加的过程。每次调用都通过闭包保存了当前的累加和，从而可以在后续调用中继续累加。这种技巧展示了 Python 函数的强大功能，特别是如何通过高阶函数和闭包来处理复杂的递归和状态保存问题。

在编程中，闭包（closure）是指函数以及它的环境，其中环境是指函数定义时所能访问到的变量。即使函数执行完成，闭包仍然能够记住并访问定义时的外部变量。我们可以通过闭包来保存一个函数的状态，确保在之后的调用中，这些状态仍然是可访问的。

例子解析

我们以 make_adder 这个例子来解释闭包的工作原理：
def make_adder(n):
    def adder(k):
        return n + k
    return adder
调用 make_adder(3) 后，它会返回一个新的 adder 函数，这个 adder 函数能够记住 n=3，即使 make_adder 函数已经结束执行，返回的 adder 仍然能够访问到 n 的值。

具体步骤如下：

定义 make_adder 函数：make_adder 函数接收一个参数 n，然后在其内部定义了一个函数 adder，这个 adder 函数也接收一个参数 k 并返回 n + k。

调用 make_adder(3)：

当我们调用 make_adder(3) 时，n 被绑定为 3，然后 make_adder 返回一个新的 adder 函数。

虽然 make_adder 已经执行完毕并退出，但由于 adder 是闭包，它仍然记住了 n=3 的值。

调用 adder：

当我们调用 adder(5) 时，它会访问到之前在 make_adder 中定义的 n=3，然后计算 3 + 5，并返回 8。

即使 make_adder 函数的执行已经结束，但因为 adder 是闭包，它能够“捕获”并保持对外部环境中 n 的引用。

闭包工作原理中的环境

当我们调用 make_adder(3) 时，程序创建了一个新的环境，我们可以通过环境图（environment diagram）来理解这个过程。

调用 make_adder(3) 时，会生成一个新的栈帧（即 f1），这个帧中会记录 n=3。

返回 adder 函数：这个 adder 函数内部使用了外部的变量 n，因此这个函数被称为“闭包”。即使 make_adder 函数执行完毕，返回的闭包 adder 依然能够访问 f1 中的 n=3。

当 adder 被调用时，它首先查找当前作用域中的变量 k，然后查找其父作用域中的 n，最终找到 f1 中的 n=3。

这就是闭包的关键——即使外部函数的执行已经结束，内部函数仍然可以访问定义时的外部变量。

深入理解：尽管 make_adder 函数已经执行完毕并返回，但由于 adder 是闭包，它依然可以访问 f1 中的 n=3。

在 make_adder(3) 执行后，make_adder 返回的 adder 函数实际上形成了一个闭包。这个闭包不仅包含了函数 adder 的定义，还包含了它所依赖的外部变量 n=3，而这个 n 是在 make_adder 的执行过程中定义的。闭包会“捕获”这个环境，并将其保留，确保在未来调用 adder 时，仍然能够使用 n=3。

这意味着，即使 make_adder 函数执行完并且返回了 adder 函数，adder 依然能够访问 make_adder 执行时的变量 n。这是因为 adder 形成的闭包“保留”了 f1 中的上下文环境。

总结

闭包是指函数及其定义时的环境的组合，允许内部函数访问外部函数的变量，即使外部函数已经执行完毕。

在 make_adder 的例子中，尽管 make_adder 函数已经返回，adder 作为闭包，仍然能够访问 make_adder 中的 n，并保持 n 的值在随后的调用中有效。

Function Composition

下面用另一个例子讨论如何使用高阶函数来创建函数组合，以及引入函数柯里化的概念。

柯里化（Currying）是将一个多参数函数转化为一系列单参数函数的过程。例如，传统的 add(x, y) 函数可以通过柯里化转换为一个只接受一个参数的函数，这个函数返回另一个接受一个参数的函数。通过这种方式，我们可以分阶段传递参数。

柯里化的示例

make_adder 是一个高阶函数，它接收一个参数 n，然后返回一个新的函数，这个新的函数接收参数 k 并返回 n + k。

def make_adder(n):
    return lambda k: n + k

通过这个函数，我们可以创建类似 add_two = make_adder(2) 这样的函数，然后调用 add_two(3) 来获得结果 5。

实现柯里化

在这个例子中，函数 curry_two 被用来将一个接收两个参数的函数（例如 add(x, y)）转换为一个高阶函数，这个高阶函数可以逐步接收每个参数，并最终返回结果。柯里化的过程如下：

def curry_two(f):
    def g(x):
        def h(y):
            return f(x, y)
        return h
    return g

curry_two 函数首先接收一个函数 f，然后返回一个新函数 g，g 接收第一个参数 x 并返回另一个函数 h，h 接收第二个参数 y，最终调用 f(x, y) 计算结果。

例如：

curried_add = curry_two(add)
add_three = curried_add(3)
print(add_three(5))  # 输出 8

这里，curried_add 是对 add 函数进行柯里化后的版本，而 add_three 是通过柯里化后创建的一个新函数，它可以接收第二个参数并返回结果。

柯里化（Currying）是函数式编程中的一个重要概念，它允许我们将多参数函数转换为链式调用的单参数函数。这种技术在构建灵活的高阶函数时非常有用。通过柯里化，我们可以逐步传递参数，延迟计算，并在需要时动态组合不同的函数。

柯里化的发明归功于 Moses Schönfinkel，而其推广者 Haskell Curry 则进一步使得这一概念广为人知。

函数组合的环境图

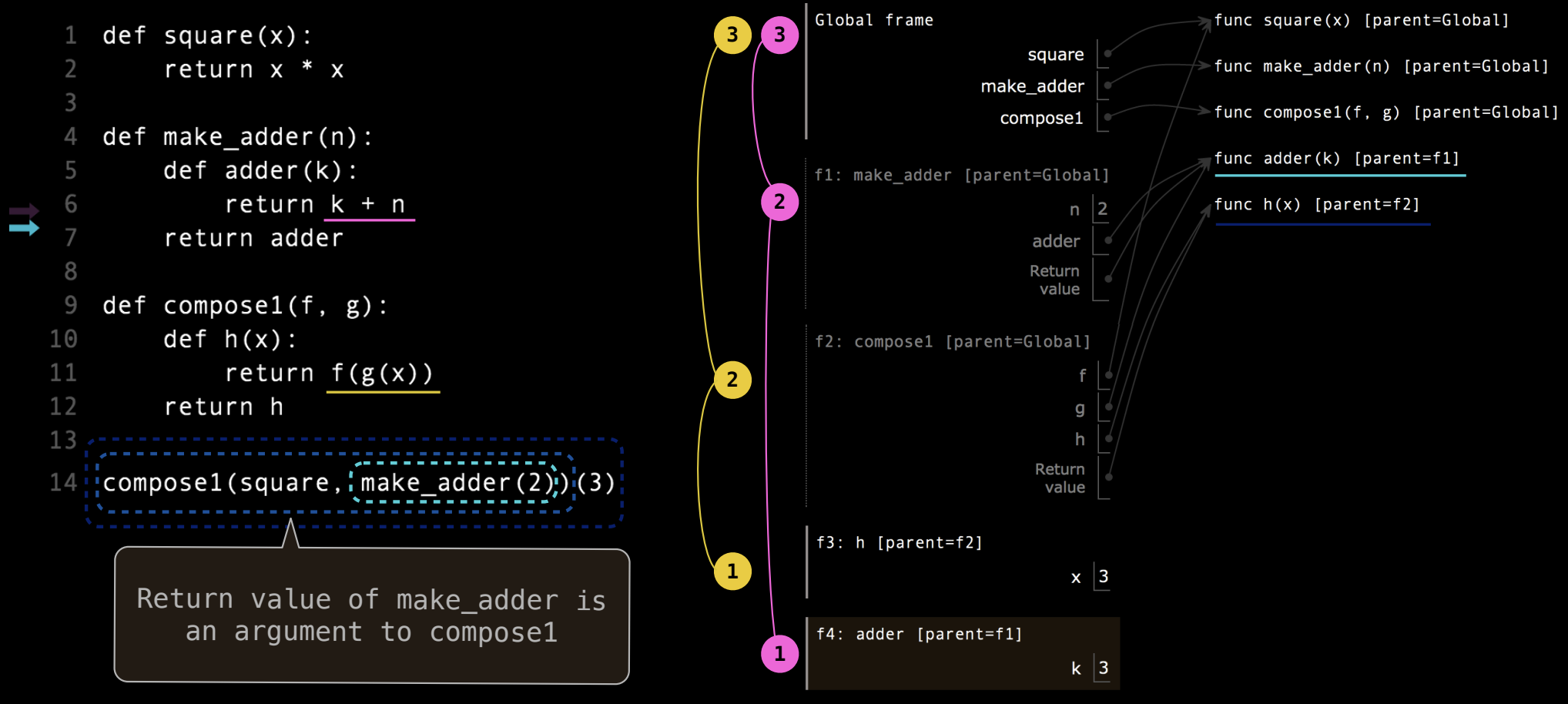
在编程中，函数组合是一个强大且常见的技巧，它允许将多个函数组合在一起，从而构建新的函数。通过组合函数，输出一个函数的结果可以作为输入传递给下一个函数。在这个例子中，我们展示了如何使用 compose1 函数将两个函数组合在一起，并分析了它的执行过程和对应的环境图。

1. 函数定义

square(x) 函数
def square(x):
    return x * x
这个函数接受一个参数 x，并返回 x 的平方。例如，square(3) 返回 9。

make_adder(n) 函数
def make_adder(n):
    def adder(k):
        return k + n
    return adder
这个函数是一个高阶函数，它接收一个参数 n，并返回一个内部定义的 adder(k) 函数。adder 函数可以接受参数 k，并将其与 n 相加。例如，make_adder(2) 返回一个能够对任意 k 加 2 的函数。

compose1(f, g) 函数
def compose1(f, g):
    def h(x):
        return f(g(x))
    return h
compose1 是一个函数组合器，它接收两个函数 f 和 g，并返回一个新的函数 h(x)。这个新函数 h(x) 首先计算 g(x)，然后将 g(x) 的结果作为 f 的输入进行计算。这个函数组合的执行顺序是从右到左的：首先执行 g(x)，再执行 f(g(x))。

2. 函数调用与环境图

现在，我们分析以下代码的执行过程：
compose1(square, make_adder(2))(3)
步骤 1：调用 make_adder(2)

当 make_adder(2) 被调用时，它返回一个 adder(k) 函数，该函数可以接受参数 k，并返回 k + 2。

在环境图中，adder(k) 函数在帧 f1 中被定义，n 的值为 2，并且 adder 函数捕获了外部变量 n = 2。

步骤 2：调用 compose1(square, make_adder(2))

compose1(square, make_adder(2)) 被调用，它返回一个新的组合函数 h(x)。

在环境图中，compose1 在帧 f2 中被调用，其中 f 绑定到 square 函数，g 绑定到 adder(k) 函数。h(x) 是 compose1 返回的组合函数，它定义在帧 f3 中。

步骤 3：调用 h(3)

最后，我们调用组合函数 h(3)。在 h(x) 中，首先计算 g(3)，即 adder(3)，该函数返回 3 + 2 = 5。

然后，将 5 作为 square 函数的输入，计算 square(5)，返回 5 * 5 = 25。

因此，最终的返回值是 25。

3. 环境图解析

全局帧（Global Frame）：在全局帧中，定义了 square、make_adder 和 compose1 函数，它们绑定到相应的函数对象。

帧 f1（make_adder 的局部帧）：f1 是 make_adder(2) 调用时创建的局部帧，在这个帧中，n = 2。该帧返回了 adder(k) 函数，adder 捕获了 n 的值。

帧 f2（compose1 的局部帧）：f2 是 compose1(square, make_adder(2)) 调用时创建的局部帧。在这个帧中，f 绑定到 square，g 绑定到 adder(k)。

帧 f3（组合函数 h(x) 的局部帧）：f3 是 h(3) 被调用时创建的帧。在这个帧中，首先计算 g(3)，然后将结果传递给 f，即 square(5)，最终返回 25。

4. 总结

在这个例子中，通过 compose1 函数，我们将 square 和 make_adder(2) 组合在一起，创建了一个新的函数 h(x)，它首先对 x 加 2，然后对结果求平方。通过环境图，我们可以清晰地看到每一步的函数调用过程，以及各个函数的作用域和它们捕获的变量值。

函数组合是编程中的一个重要技巧，特别是在需要将多个操作串联起来的情况下。通过将简单的函数组合在一起，我们可以创建出功能强大且灵活的工具，同时保持代码的简洁与模块化。

Lecture 5. Environments

Announcements

考试规则

Environments for Higher-Order Functions

环境图中的高阶函数

高阶函数的进一步应用

关键概念

嵌套定义的环境

高阶函数 make_adder 的执行过程

关键概念总结：

1. 局部变量和作用域：

2. 嵌套函数和闭包：

3. 函数组合与高阶函数：

4. 环境图的具体构建：

5. 总结与要点：

Local Names

def 语句

lambda 表达式

关键区别

示例：递归函数 print_sums

过程解析

环境图解析

例子解析

闭包工作原理中的环境

深入理解：尽管 make_adder 函数已经执行完毕并返回，但由于 adder 是闭包，它依然可以访问 f1 中的 n=3。

总结

Function Composition

柯里化的示例

实现柯里化

函数组合的环境图

1. 函数定义

2. 函数调用与环境图

3. 环境图解析

4. 总结

高阶函数 `make_adder` 的执行过程

`def` 语句

`lambda` 表达式

示例：递归函数 `print_sums`

深入理解：尽管 `make_adder` 函数已经执行完毕并返回，但由于 `adder` 是闭包，它依然可以访问 `f1` 中的 `n=3`。