Lecture 14. Circuits (optional)

Announcements

项目和时间提醒：

项目二的截止日期是周五，请确保在今天提交第一阶段任务，以获得检查点分数。
如果能在周四前提交整个项目，可以获得提前提交的加分。

课程讲座：

今天的讲座以及周一的讲座不会出现在考试或作业中，但内容非常有趣，鼓励同学们观看并提出问题。
辅导预约将在周五、周六和下周一提供。标注为“Advising”的预约仅用于咨询辅导，而不是作业或项目帮助。如果需要作业帮助，请选择其他位置的预约。

Circuits 逻辑电路与计算机的核心工作原理

从布尔运算到电路：

我们已经知道，通过使用二进制数（仅包含 0 和 1）可以表示正数、负数以及浮点数。
通过布尔运算的基本操作——逻辑与（AND）、逻辑或（OR）和逻辑非（NOT）——可以实现逻辑运算。我们还知道如何使用晶体管来物理实现这些布尔操作：
- 两个串联的晶体管可以构建与门（AND Gate）；
- 两个并联的晶体管可以构建或门（OR Gate）；
- 一个晶体管和一个电阻可以构建非门（NOT Gate）。

电路的定义：

电路是一个由逻辑门（AND、OR、NOT）组成的集合，其功能是将一组二进制输入转换为一组二进制输出。电路本质上是一个函数，通过对输入进行逻辑运算，产生相应的输出。

电路示例：

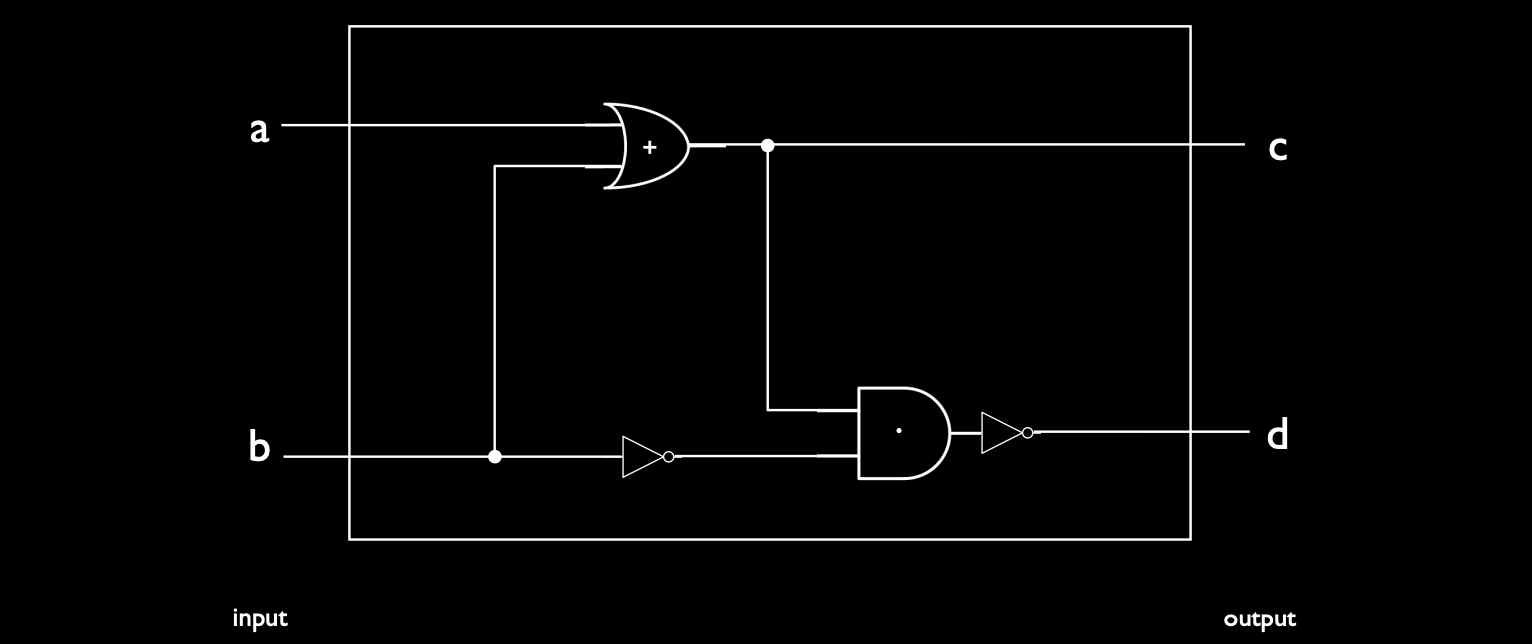
让我们看一个简单的电路示例，虽然这个电路目前没有实际的计算意义，但它展示了电路的结构和工作方式。
电路输入和输出：电路从左侧接收两个输入 \(A\) 和 \(B\)，它们可以是 0 或 1（二进制），并输出 \(C\) 和 \(D\)，它们也是 0 或 1。
门电路的工作：
- 首先，\(A\) 和 \(B\) 进入一个或门（OR Gate），输出为 \(A \lor B\)。
- 接着，\(B\) 通过一个分叉，一部分输入到非门，生成 \( \neg B \)，然后 \( \neg B \) 和 \(A \lor B\) 进入一个与门（AND Gate）。
- 最后，对 \(A \lor B\) 和 \( \neg B \) 的与操作的结果进行非操作，生成最终输出 \(D\)。

电路表达式的推导：

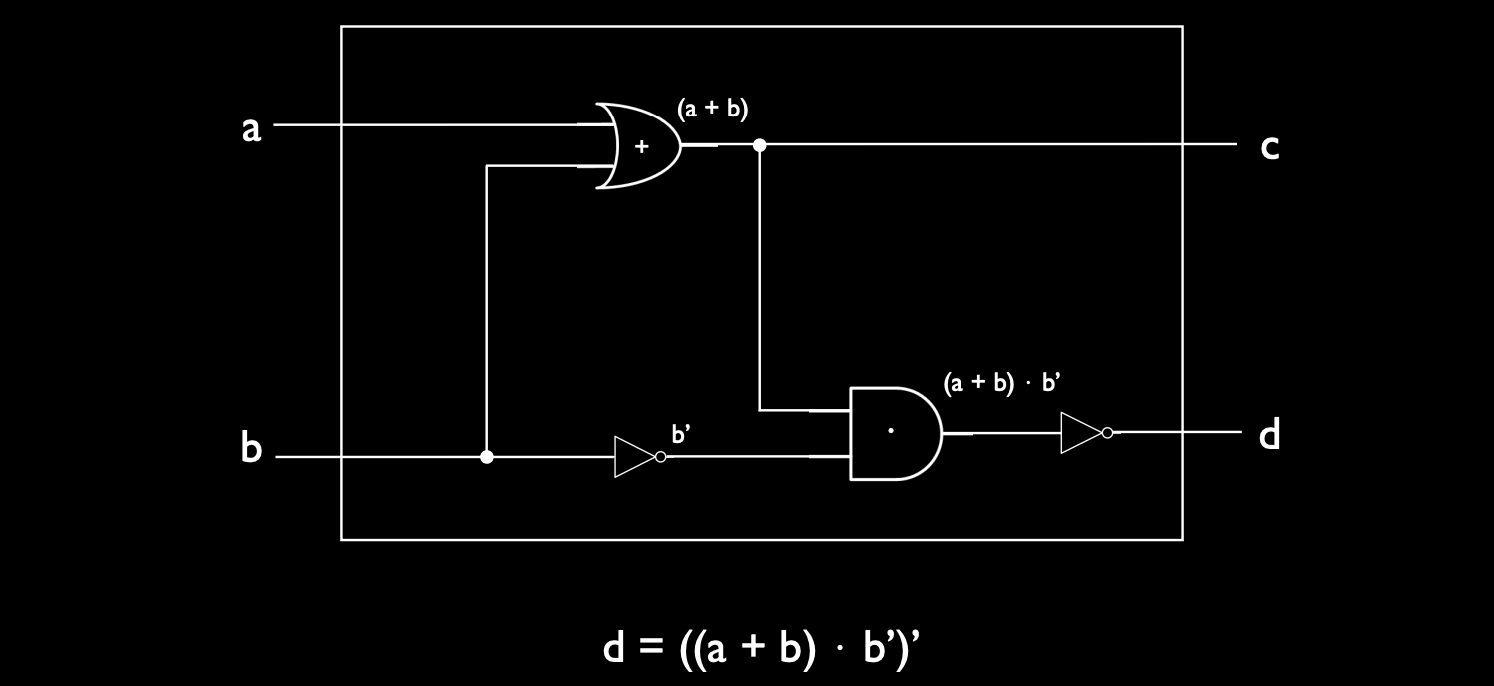
通过电路的运算逻辑，可以推导出输出 \(D\) 的表达式： \[ D = \neg ((A \lor B) \land \neg B) \]
这个表达式展示了如何通过逻辑门组合来计算一个复杂的布尔表达式。

电路的抽象与复杂计算：

我们可以使用这些简单的逻辑门（AND、OR、NOT）来实现更多复杂的逻辑和计算功能。
加法器（Adder）就是其中一个经典示例，通过组合多个逻辑门，可以实现二进制加法操作。这样的加法器是现代计算机中处理算术运算的基础组件之一。

Designing Circuits

步骤一：真值表的构建

为了实现具体的计算，我们需要构建真值表，这是描述所有可能输入组合及其相应输出的表格。我们首先确定输入和输出的数量，然后列出所有可能的输入组合，并为每个输入组合指定相应的输出。

假设我们有两个输入 \(A\) 和 \(B\)，我们需要构建一个两输入的真值表。对于两个输入，我们有 \(2^2 = 4\) 种可能的输入组合，这意味着真值表将有四行，分别是：

这是任何两输入电路的输入部分。接下来我们要确定输出。假设我们想要计算输出 \(C\) 和 \(D\)，可以根据具体需求设置输出条件。例如，假设输出 \(C\) 为 1 的条件是 \(A = 1\) \(B = 0\) 或者 \(A = 0\) \(B = 1\) ，输出 \(D\) 为 1 的条件是 \(A = 1\) 且 \(B = 1\)。这样，真值表的输出部分就可以表示为：

步骤二：构建子表达式

我们通过观察真值表中的输出为 1 的情况来构建对应的子表达式：

构建 \(D\) 的表达式：

\(D\) 只有在 \(A = 1\) 且 \(B = 1\) 时输出为 1，因此 \(D\) 的表达式为： \[ D = A \land B \] 这个表达式捕获了 \(D\) 输出为 1 的情况。

构建 \(C\) 的表达式：

\(C\) 在两种情况下输出为 1：当 \(A = 0, B = 1\) 或 \(A = 1, B = 0\)。因此我们需要两个子表达式来捕获这些情况：
- 当 \(A = 0, B = 1\) 时，表达式为： \[ \neg A \land B \]
- 当 \(A = 1, B = 0\) 时，表达式为： \[ A \land \neg B \]
最终，\(C\) 的完整表达式是通过 OR 运算将这两个子表达式组合在一起： \[ C = (\neg A \land B) \lor (A \land \neg B) \]

步骤三：组合子表达式

通过 OR 运算将子表达式组合，得到了完整的布尔表达式。这些表达式捕获了输入 \(A\) 和 \(B\) 的所有可能组合下的输出情况。

对于 \(C\)： \[ C = (\neg A \land B) \lor (A \land \neg B) \] 这个表达式表示当 \(A\) 和 \(B\) 的值为 (0, 1) 或 (1, 0) 时，\(C\) 输出为 1，否则为 0。
对于 \(D\)： \[ D = A \land B \] 这个表达式表示 \(D\) 只有在 \(A = 1\) 且 \(B = 1\) 时输出 1。

步骤四：画出电路图

在前面的步骤中，我们通过真值表和布尔表达式定义了输入和输出之间的关系。接下来，我们将这些布尔表达式转换为物理电路图。

电路图中的输入通常位于左侧，输出在右侧。为了设计电路，我们需要根据布尔表达式中的逻辑运算符（如 AND、OR、NOT）来连接相应的逻辑门。

处理 \(D\) 的电路：

根据布尔表达式 \(D = A \land B\)，我们可以简单地使用一个 AND 门 来实现。我们将输入 \(A\) 和 \(B\) 都接入 AND 门，并将输出接入 \(D\)。这很直接，因为 \(D\) 仅依赖于 \(A\) 和 \(B\) 的逻辑与运算。

步骤：
- 将 \(A\) 和 \(B\) 分别输入到 AND 门。
- AND 门 的输出就是 \(D\)。

处理 \(C\) 的电路：

\(C\) 的表达式更复杂，它包含两个子表达式的 OR 运算：

\[ C = (\neg A \land B) \lor (A \land \neg B) \]

这意味着我们需要使用两个 AND 门 和一个 OR 门，以及两个 NOT 门 来实现此表达式。

步骤：
- 首先，将 \(A\) 通过 NOT 门 得到 \(\neg A\)，并与 \(B\) 一起输入 AND 门，生成第一个子表达式 \(\neg A \land B\)。
- 然后，将 \(B\) 通过 NOT 门 得到 \(\neg B\)，并与 \(A\) 一起输入另一个 AND 门，生成第二个子表达式 \(A \land \neg B\)。
- 最后，将两个 AND 门 的输出输入到 OR 门，得到最终的输出 \(C\)。

完整的电路图：

为了绘制这个电路，我们需要安排好每个逻辑门的布局。通常，从输入 \(A\) 和 \(B\) 开始，依次经过 NOT 门、AND 门 和 OR 门，直到生成输出。

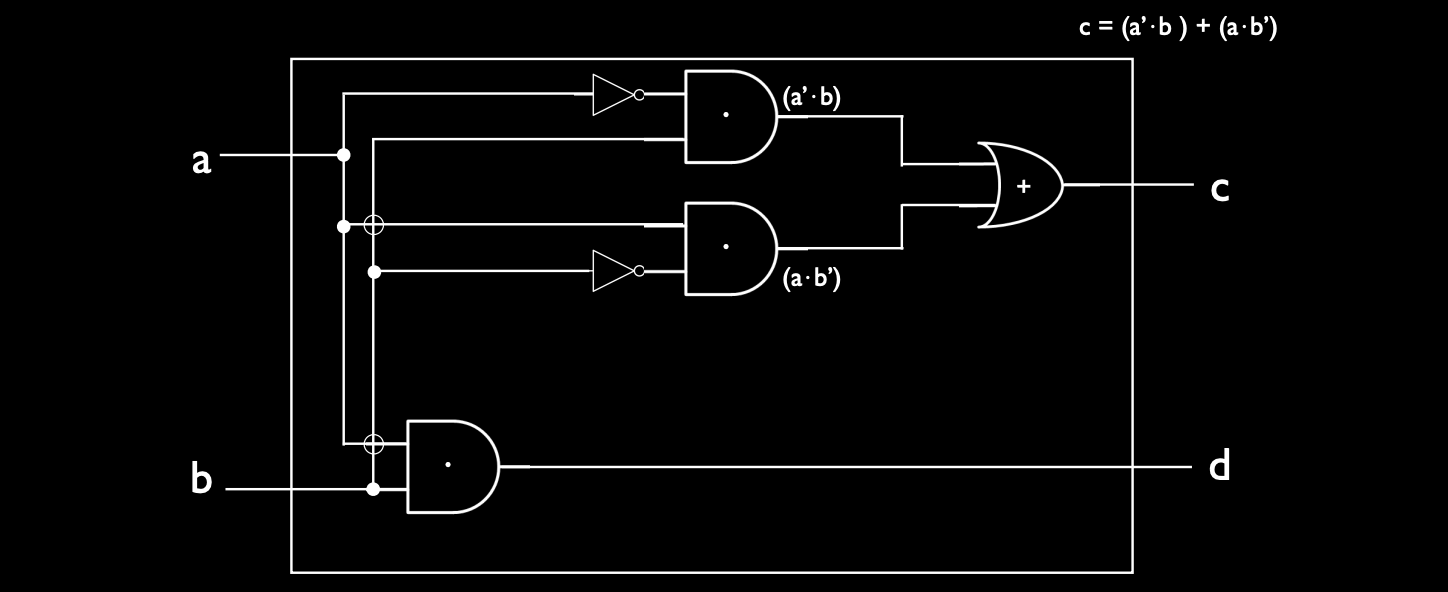
步骤概览：
- 将输入 \(A\) 和 \(B\) 分别接入 AND 门 和 NOT 门。
- 将 NOT 门 的输出与对应的另一个输入一起接入 AND 门，得到两个子表达式。
- 最后，将两个子表达式通过 OR 门 组合，生成 \(C\) 的输出。

复习四个步骤

建立真值表：为输入 \(A\) 和 \(B\) 构建真值表，列出所有可能的输入组合和相应的输出。
构建子表达式：为每个输出构建逻辑表达式，仅使用 AND 和 NOT。每个输出列都是独立的。
组合子表达式：使用 OR 运算将所有子表达式组合在一起，生成最终的布尔表达式。
画出电路图：根据生成的布尔表达式绘制电路图，连接相应的逻辑门。

下一步：实际计算

现在我们已经完成了基本的电路设计，包括使用 AND、OR 和 NOT 门进行简单逻辑运算的实现。接下来，我们将继续探讨如何利用这些基本电路执行更复杂和有意义的计算，例如加法、乘法等。

设计一个一位比较电路（One-Bit Compare for Equality Circuit）

现在我们已经理解了电路设计的基础步骤，接下来将通过一个实际例子来实现一个有意义的计算——一位比较电路。这个电路的作用是比较两个输入位 \(A\) 和 \(B\) 是否相等，并输出相应的结果。

问题定义

我们需要构建一个电路来比较两个一位二进制输入 \(A\) 和 \(B\) 是否相等。输出 \(C\) 为 1 表示两位相等，输出 \(C\) 为 0 表示它们不相等。

伪代码：

if A == B then 
    return 1
else 
    return 0

输入和输出都是二进制数。我们将基于这一需求设计一个逻辑电路，接下来详细说明步骤。

步骤一：构建真值表

首先，我们需要列出所有可能的输入组合，以及它们对应的输出 \(C\) 值。这里 \(A\) 和 \(B\) 都是一位二进制数，因此有四种输入组合：

在此真值表中，只有当 \(A\) 和 \(B\) 相等时（即 \(A = B\)），输出 \(C\) 才为 1，否则为 0。

步骤二：构建子表达式

现在我们需要为输出 \(C\) 构建逻辑表达式。通过真值表，我们可以看到 \(C\) 在两种情况下为 1：当 \(A = 0\) 且 \(B = 0\)，或者当 \(A = 1\) 且 \(B = 1\)。

当 \(A = 0\) 且 \(B = 0\) 时，我们可以使用 NOT 门 将 \(A\) 和 \(B\) 的值取反，然后通过 AND 门 进行组合。因此，该子表达式为： \[ \neg A \land \neg B \]
当 \(A = 1\) 且 \(B = 1\) 时，直接通过 AND 门 将 \(A\) 和 \(B\) 组合。因此，该子表达式为： \[ A \land B \]

步骤三：合并子表达式

现在我们需要通过 OR 门 将这两个子表达式组合在一起，得到完整的逻辑表达式：

\[ C = (\neg A \land \neg B) \lor (A \land B) \]

这个表达式表示，当 \(A\) 和 \(B\) 均为 0 或均为 1 时，输出 \(C\) 为 1，否则为 0。

步骤四：画出电路图

最后一步是将上述布尔表达式转换为电路图。

输入：左侧有两个输入 \(A\) 和 \(B\)。
逻辑门：
- 使用两个 NOT 门 对 \(A\) 和 \(B\) 进行取反。
- 使用两个 AND 门 组合 \(A\) 和 \(B\) 的正反值。
- 使用一个 OR 门 合并两个 AND 门 的输出。
输出：右侧输出 \(C\)，表示比较结果。

电路图的步骤：

将输入 \(A\) 和 \(B\) 连接到两个 NOT 门，分别生成 \(\neg A\) 和 \(\neg B\)。
使用 AND 门 将 \(\neg A\) 和 \(\neg B\) 组合，得到 \(\neg A \land \neg B\)。
使用另一个 AND 门 将 \(A\) 和 \(B\) 组合，得到 \(A \land B\)。
最后，将两个 AND 门 的输出输入到 OR 门，生成输出 \(C\)。

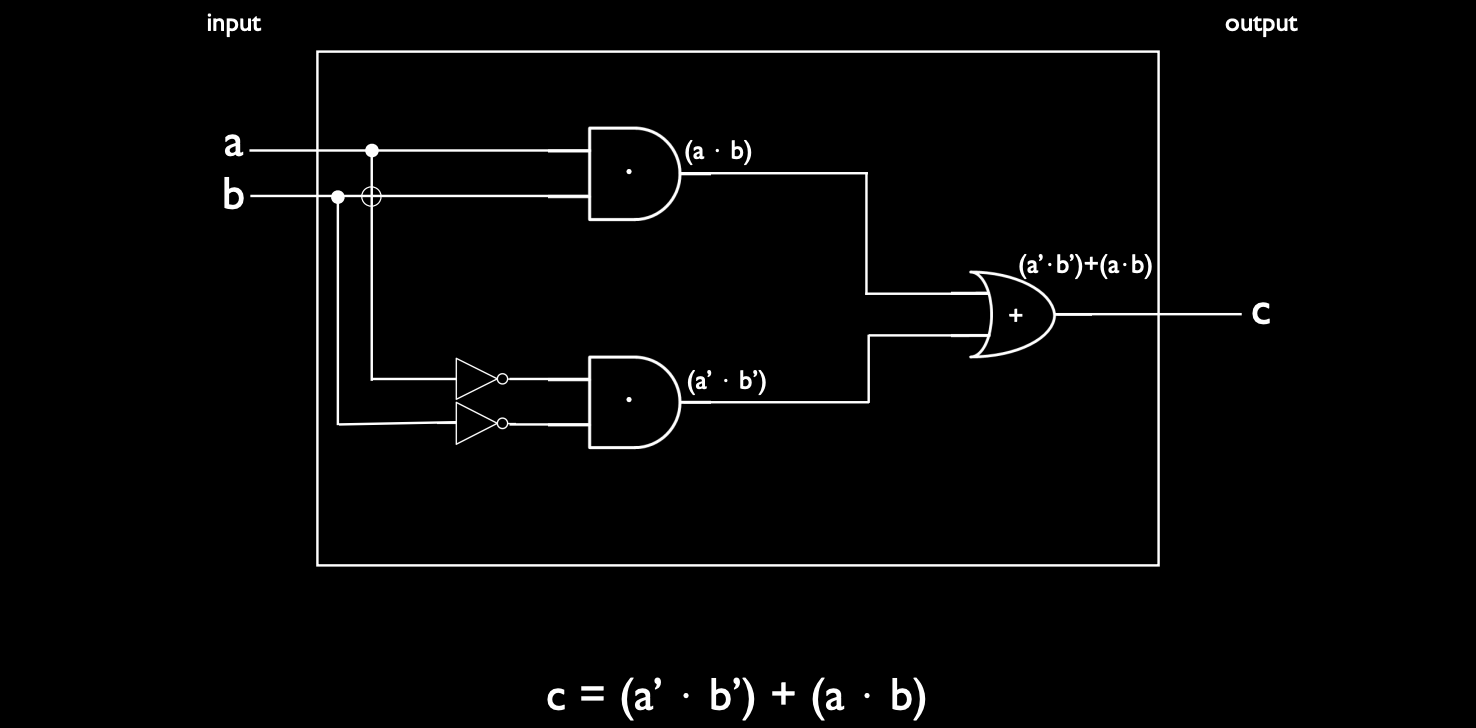
通过上述四个步骤，我们成功地构建了一个一位比较电路。这个电路可以判断两个一位二进制数是否相等，并输出 1 或 0。虽然这个电路比较简单，但它展示了从真值表、布尔表达式到实际电路设计的完整过程。

四位比较电路设计 4-Bit Compare for Equality (CE)

现在我们要设计一个四位比较电路，它的作用是比较两个四位二进制数 \(A\) 和 \(B\) 是否相等。如果两个四位数相等，则输出 \(C\) 为 1，否则为 0。我们将基于之前设计的一位比较电路进行扩展。

问题定义

给定两个四位的二进制数 \(A\) 和 \(B\)，每个数由四个二进制位表示：

\(A = a_3 a_2 a_1 a_0\)
\(B = b_3 b_2 b_1 b_0\)

我们的目标是检查这两个四位数的每一位是否相等。也就是说，如果 \(a_3 = b_3\)、\(a_2 = b_2\)、\(a_1 = b_1\) 和 \(a_0 = b_0\)，则输出 1，否则输出 0。

步骤一：输入与输出

每个输入数 \(A\) 和 \(B\) 都包含四个位，因此我们有八个输入：\(a_3, a_2, a_1, a_0, b_3, b_2, b_1, b_0\)。输出为一个位 \(C\)，当 \(A\) 和 \(B\) 的所有位都相等时，输出为 1。真值表有\(2^8 = 256\) 行。

步骤二：设计比较逻辑

我们可以复用之前设计的一位比较电路，比较每一位的相等性。对于每一位的比较，我们使用一个一位比较器，其输出为 1 表示两个位相等，输出为 0 表示不相等。

一位比较电路复用

回顾一下一位比较电路的设计：

\[ C = (\neg A \land \neg B) \lor (A \land B) \]

这个逻辑表达式表示，当 \(A = B\) 时，输出 \(C\) 为 1。

扩展到四位比较

我们需要比较每个位的相等性，并且只有在所有位都相等时，整个比较结果才为 1。这意味着我们需要对四个一位比较器的输出做 AND 操作，只有当所有位的比较器都输出 1 时，最终输出 \(C\) 才为 1。

伪代码：

two 4-bit numbers are equal if:
 a3 == b3 and
 a2 == b2 and
 a1 == b1 and
 a0 == b0

步骤三：合并子电路

每个位的比较：将 \(a_3\) 和 \(b_3\)、\(a_2\) 和 \(b_2\)、\(a_1\) 和 \(b_1\)、\(a_0\) 和 \(b_0\) 分别输入到四个一位比较电路中。
逻辑与运算：我们将四个一位比较电路的输出通过 AND 门 组合在一起，只有当所有比较器输出 1 时，最终的输出 \(C\) 才为 1。

步骤四：画出电路图

输入：
- 输入 \(A\) 和 \(B\) 共有四位，分别为 \(a_3, a_2, a_1, a_0\) 和 \(b_3, b_2, b_1, b_0\)。
一位比较电路：
- 将每个位 \(a_i\) 和 \(b_i\) 输入到一位比较电路中。每个比较器的输出为 1 表示对应位相等，为 0 表示不相等。
逻辑与运算：
- 将四个一位比较电路的输出输入到多个 AND 门 中，逐级合并比较结果，得到最终的输出 \(C\)。

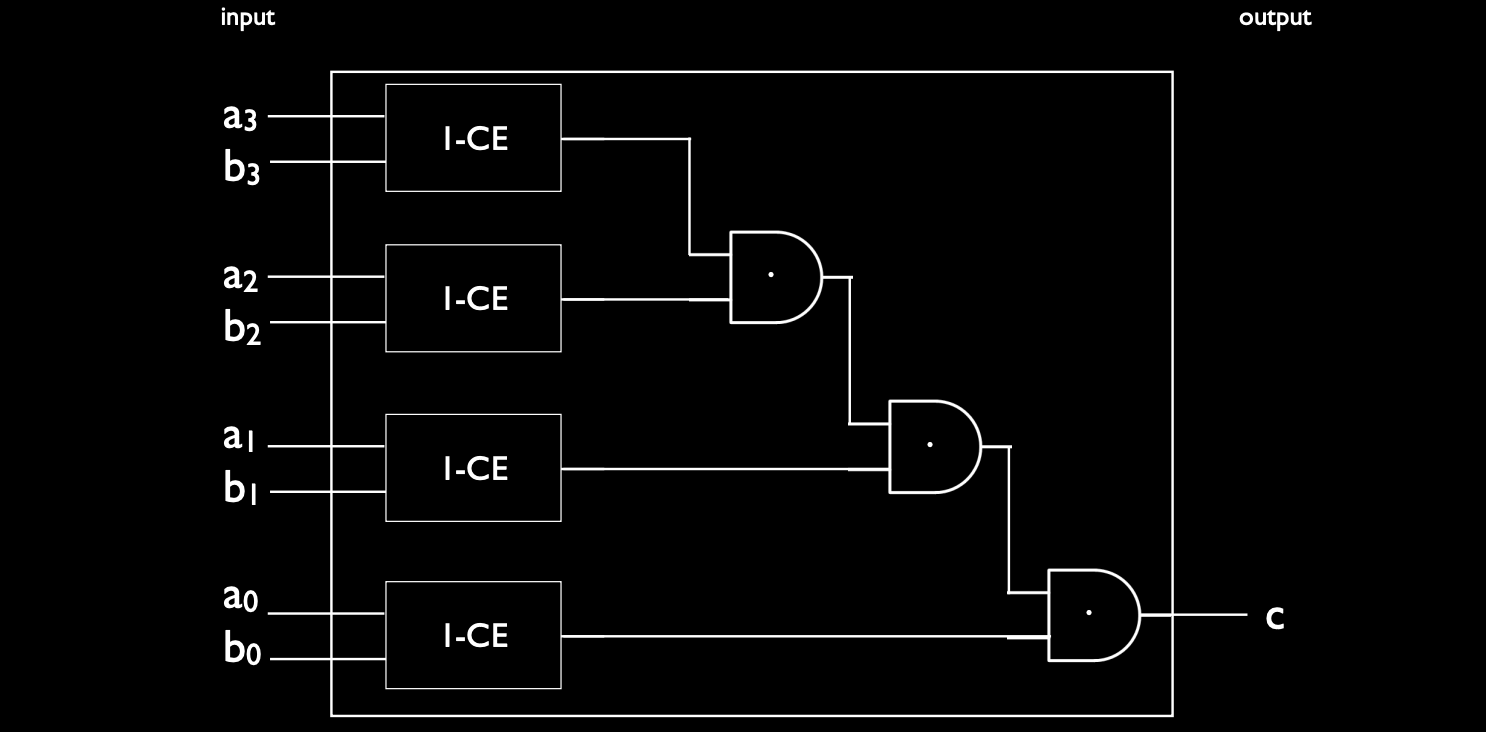
通过这个四位比较电路，我们可以比较两个四位二进制数的每一位是否相等，并输出一个布尔结果。这个设计展示了如何从简单的一位比较器扩展到更复杂的电路，同时利用逻辑门组合来完成多位数的比较。

构建加法器：从一位到四位

接下来，我们将设计一个一位加法器，然后逐步扩展到四位加法器。这是构建计算机中常见运算电路的基础。

问题定义

我们需要构建一个能够对两个一位二进制数进行加法运算的电路。输入为 \(A\) 和 \(B\)，每个输入值都是 0 或 1。加法运算结果可能产生进位，因此除了求和结果，还需要考虑进位输出。

一位加法的逻辑

让我们回顾一下二进制加法的基本规则：

\(0 + 0 = 0\)
\(0 + 1 = 1\)
\(1 + 0 = 1\)
\(1 + 1 = 10\) （即和为 0，有一个进位）

因此，单次二进制加法有两个输出：

求和：即当前位的加法结果。
进位：当两个输入位都为 1 时，产生进位。

真值表

我们首先需要构建一个真值表，列出所有可能的输入组合及其对应的求和输出（Sum）和进位输出（Carry）。

A	B	Sum	Carry
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

布尔表达式

根据真值表，我们可以得出每个输出的布尔表达式。

求和（Sum）：
- 当 \(A\) 和 \(B\) 不相同时，求和为 1。因此，求和可以表示为： \[ \text{Sum} = A \oplus B \] 这里，\(\oplus\) 表示异或（XOR）运算。
进位（Carry）：
- 当 \(A = 1\) 且 \(B = 1\) 时，产生进位。因此，进位可以表示为： \[ \text{Carry} = A \land B \]

电路设计

我们可以基于上述布尔表达式设计一个一位加法器电路。

输入：两个输入 \(A\) 和 \(B\)。
异或门（XOR 门）：用于计算求和 \(\text{Sum}\)。
与门（AND 门）：用于计算进位 \(\text{Carry}\)。

一位全加器

在实际计算中，我们不仅需要考虑两个输入位的加法，还要考虑可能来自上一位的进位。因此，我们需要构建一个全加法器（Full Adder），它有三个输入：\(A\)、\(B\) 和来自上一位的进位 \(C_{\text{in}}\)，并输出两个结果：求和 \(S\) 和 进位输出 \(C_{\text{out}}\)。

真值表

A	B	\(C_{\text{in}}\)	Sum	\(C_{\text{out}}\)
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

布尔表达式

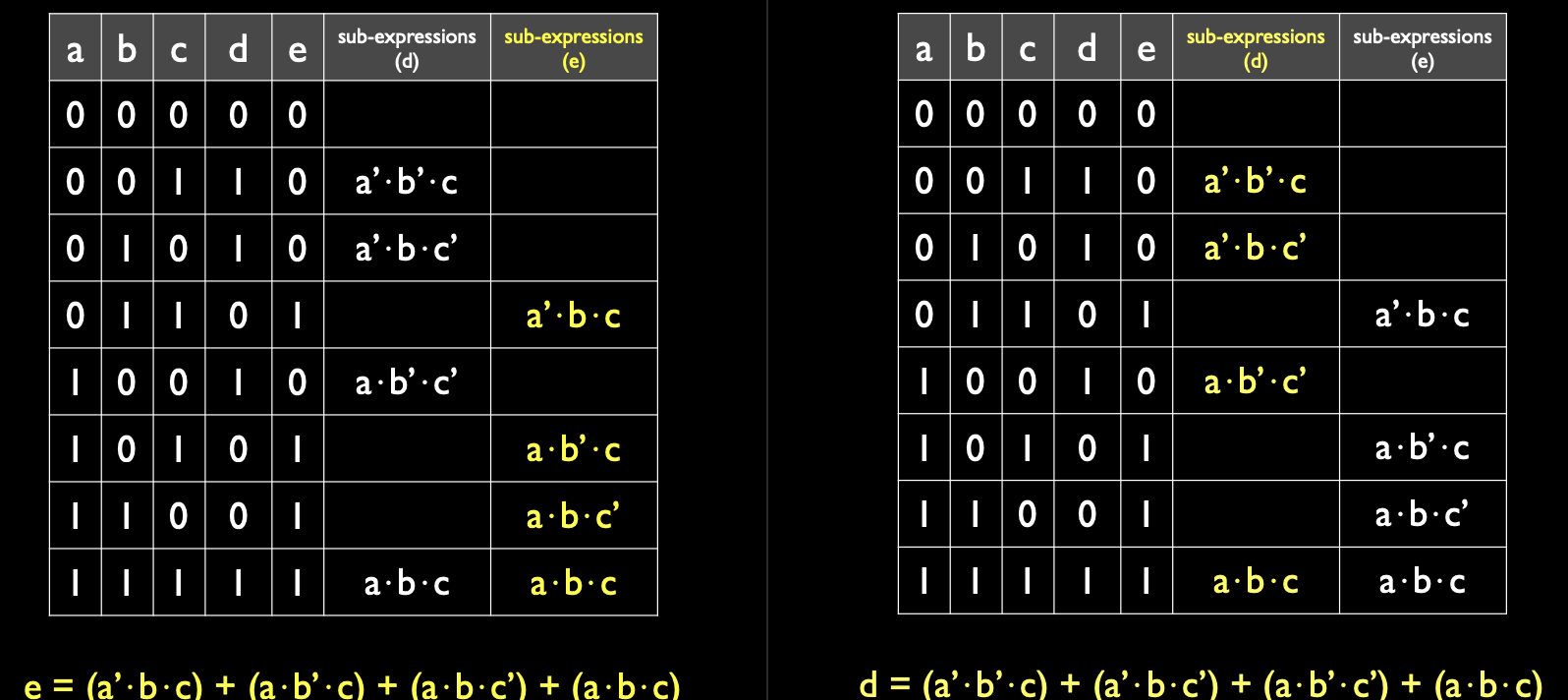
构建子表达式

接下来我们通过分析真值表，分别为和（Sum）和进位（Carry Out）构建子表达式。我们需要关注每个输出为 1 的行。

对于 Sum：

第 2 行：\(A = 0, B = 0, C_{\text{in}} = 1\)，输出 1。子表达式为： \[ \text{Sum} = \neg A \land \neg B \land C_{\text{in}} \]
第 3 行：\(A = 0, B = 1, C_{\text{in}} = 0\)，输出 1。子表达式为： \[ \text{Sum} = \neg A \land B \land \neg C_{\text{in}} \]
第 5 行：\(A = 1, B = 0, C_{\text{in}} = 0\)，输出 1。子表达式为： \[ \text{Sum} = A \land \neg B \land \neg C_{\text{in}} \]
第 8 行：\(A = 1, B = 1, C_{\text{in}} = 1\)，输出 1。子表达式为： \[ \text{Sum} = A \land B \land C_{\text{in}} \]

最终的 Sum 表达式为： \[ \text{Sum} = (\neg A \land \neg B \land C_{\text{in}}) \lor (\neg A \land B \land \neg C_{\text{in}}) \lor (A \land \neg B \land \neg C_{\text{in}}) \lor (A \land B \land C_{\text{in}}) \]

对于 Carry Out：

第 4 行：\(A = 0, B = 1, C_{\text{in}} = 1\)，输出 1。子表达式为： \[ \text{Carry Out} = \neg A \land B \land C_{\text{in}} \]
第 6 行：\(A = 1, B = 0, C_{\text{in}} = 1\)，输出 1。子表达式为： \[ \text{Carry Out} = A \land \neg B \land C_{\text{in}} \]
第 7 行：\(A = 1, B = 1, C_{\text{in}} = 0\)，输出 1。子表达式为： \[ \text{Carry Out} = A \land B \land \neg C_{\text{in}} \]
第 8 行：\(A = 1, B = 1, C_{\text{in}} = 1\)，输出 1。子表达式为： \[ \text{Carry Out} = A \land B \land C_{\text{in}} \]

最终的 Carry Out 表达式为： \[ \text{Carry Out} = (\neg A \land B \land C_{\text{in}}) \lor (A \land \neg B \land C_{\text{in}}) \lor (A \land B \land \neg C_{\text{in}}) \lor (A \land B \land C_{\text{in}}) \]

步骤 3：构建电路

根据布尔表达式，我们可以用逻辑门（与门、或门、非门）来构建电路。以下是构建全加器电路的步骤：

输入：三个输入 \(A\)、\(B\)、\(C_{\text{in}}\)。
逻辑门：
- 异或门（XOR 门）：用于计算求和（Sum）。
- 与门（AND 门）：用于计算进位（Carry Out）。
- 或门（OR 门）：用于将多个进位条件组合起来。

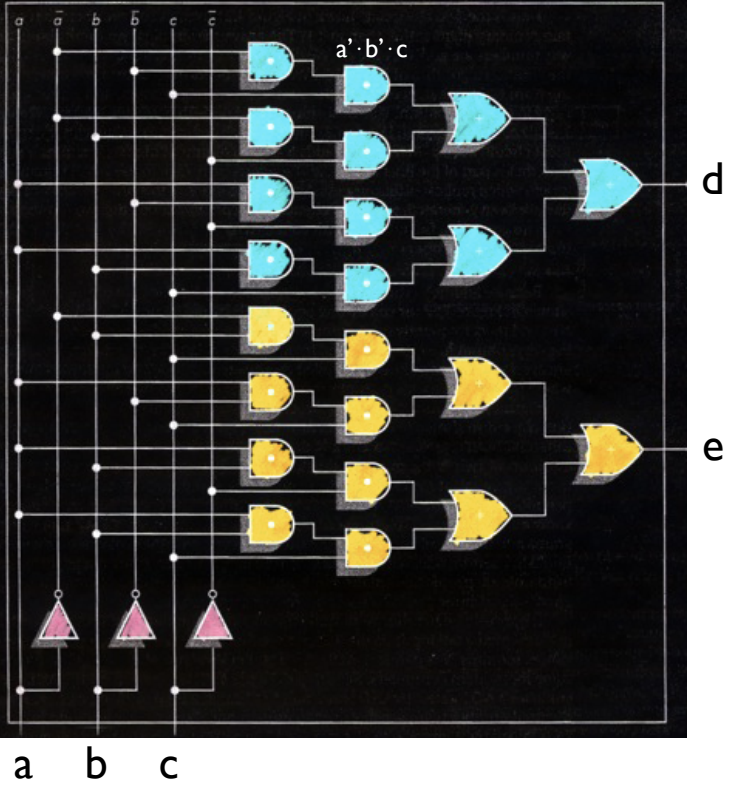
通过设计全加器，我们不仅解决了单比特加法的问题，还为多位二进制加法器的扩展奠定了基础。

构建四位加法器电路

现在我们要构建一个 四位加法器，用于对两个四位二进制数进行加法运算。之前我们已经完成了 一位加法器 的设计，现在我们将其扩展为四位加法器。

设计思路

我们将使用四个一位加法器，每个一位加法器负责计算对应的两个二进制位的和以及产生的进位。每个一位加法器的进位输出将作为下一个更高位加法器的进位输入。

一位加法器回顾

我们之前已经构建了一位加法器，其输入为三个比特（两个数的对应位以及从前一位进位的 Carry In），输出为和（Sum）和进位（Carry Out）。我们通过布尔表达式和逻辑门实现了这一功能。

一位加法器的输入和输出如下：

输入：\( A \), \( B \), \( C_{\text{in}} \)
输出：\( \text{Sum} \), \( C_{\text{out}} \)

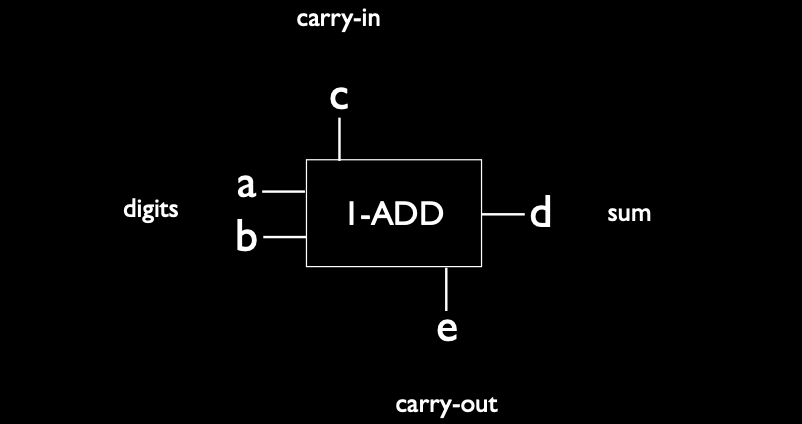
为了构建四位加法器，我们将使用四个一位加法器，将其串联起来。每个一位加法器计算相应位的加法，并将进位传递给下一个高位。

四位加法器电路

输入：
- 两个四位二进制数 \( A_3, A_2, A_1, A_0 \) 和 \( B_3, B_2, B_1, B_0 \)。
- 进位输入 \( C_{\text{in}} \)，通常从最低位开始 \( C_{\text{in}} = 0 \)。
输出：
- 四位和 \( \text{Sum}_3, \text{Sum}_2, \text{Sum}_1, \text{Sum}_0 \)。
- 最后的进位输出 \( C_{\text{out}} \)。

电路实现

我们将通过四个一位加法器逐步完成四位加法：

第 0 位加法：
- 输入：\( A_0, B_0, C_{\text{in}} \)。
- 输出：\( \text{Sum}_0 \) 和 \( C_1 \)（作为第 1 位加法的进位输入）。
第 1 位加法：
- 输入：\( A_1, B_1, C_1 \)。
- 输出：\( \text{Sum}_1 \) 和 \( C_2 \)（作为第 2 位加法的进位输入）。
第 2 位加法：
- 输入：\( A_2, B_2, C_2 \)。
- 输出：\( \text{Sum}_2 \) 和 \( C_3 \)（作为第 3 位加法的进位输入）。
第 3 位加法：
- 输入：\( A_3, B_3, C_3 \)。
- 输出：\( \text{Sum}3 \) 和最终的进位 \( C{\text{out}} \)。
溢出处理：

如果最高位加法器的进位输出为 1，说明加法结果超出了四位的范围，此时产生溢出（Overflow）。为了简化，我们在这里忽略溢出的处理，但在实际电路设计中，溢出可以通过额外的处理逻辑来捕获。

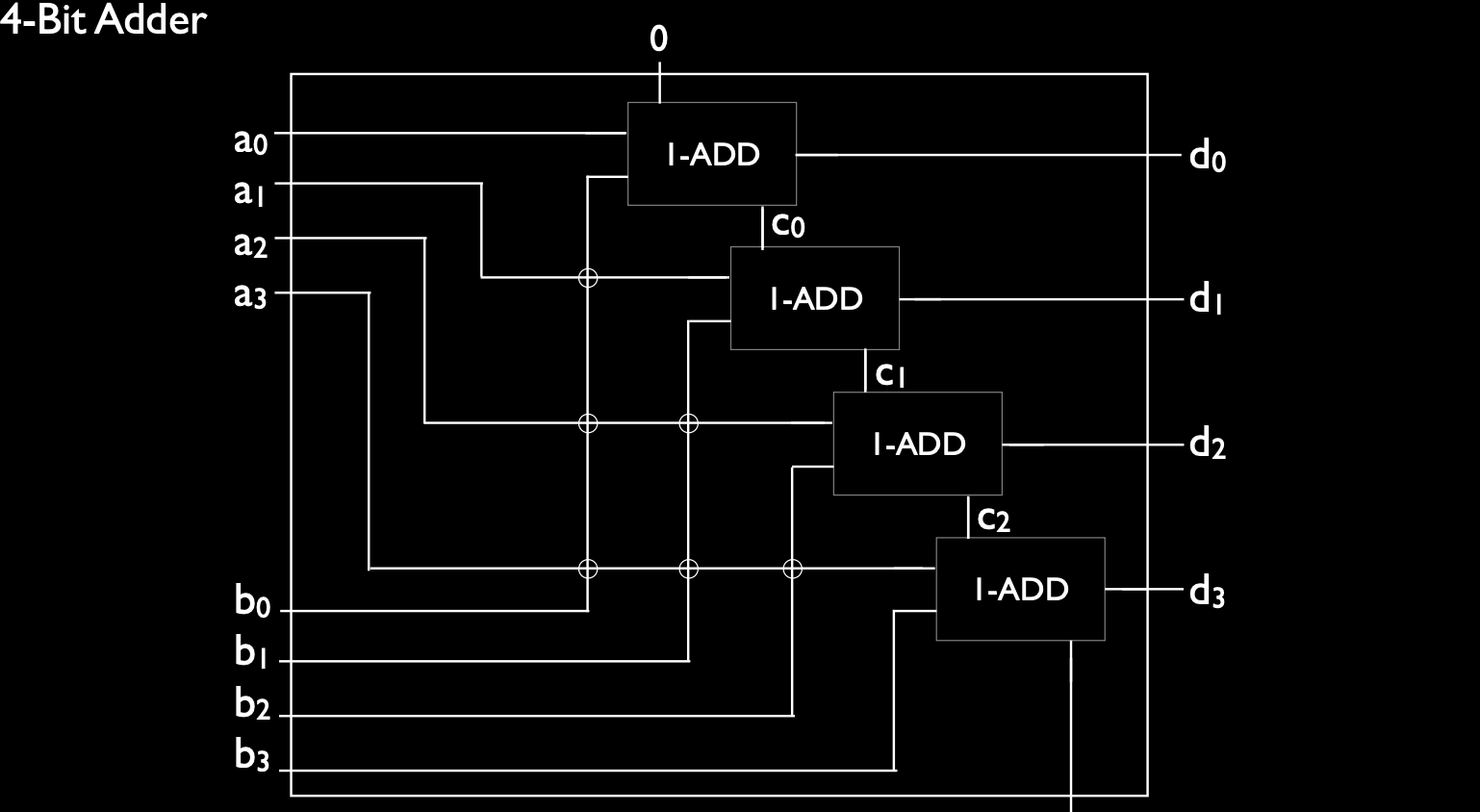
抽象的电路设计

通过利用一位加法器的抽象，我们可以很容易地将其扩展到四位加法器。如下是四位加法器的工作流程：

最低位加法器：将 \( A_0 \)、\( B_0 \) 和进位输入 0 输入一位加法器，输出 \( \text{Sum}_0 \) 和进位 \( C_1 \)。
第 1 位加法器：接收 \( A_1 \)、\( B_1 \) 和进位 \( C_1 \)，输出 \( \text{Sum}_1 \) 和进位 \( C_2 \)。
第 2 位加法器：接收 \( A_2 \)、\( B_2 \) 和进位 \( C_2 \)，输出 \( \text{Sum}_2 \) 和进位 \( C_3 \)。
第 3 位加法器：接收 \( A_3 \)、\( B_3 \) 和进位 \( C_3 \)，输出 \( \text{Sum}3 \) 和进位 \( C{\text{out}} \)。

电路效率问题

通过简单的逻辑门和一位加法器的组合，我们已经可以构建功能完善的四位加法器。然而，这样的电路设计随着位数的增加会变得非常复杂：

每位的逻辑门数量：
- 一位加法器中包含多个与门、或门、非门。为了实现 32 位加法器，我们需要大量的逻辑门和晶体管。
- 一个 32 位加法器大约需要 96 个非门、512 个与门、192 个或门，这意味着大约需要 1500 个晶体管。
现代计算机的优势：
- 现代计算机能够将这些逻辑门和晶体管缩小到极小的物理尺寸，因此可以在微小的芯片上实现复杂的运算功能。

专用电路设计：判断一个八位二进制数是否为零

在这部分，我们将设计一个专用的电路，用于判断一个八位二进制数是否为零。这是计算中非常常见的操作，比如在计数时需要判断计数器是否已到零，或者在除法中检查除数是否为零。因此，设计一个专用电路来快速执行这一操作是非常有用的。

电路设计的步骤

输入和输出：
- 输入：一个八位二进制数 \( A \)，表示为 \( A_7, A_6, A_5, A_4, A_3, A_2, A_1, A_0 \)，总共有八个输入位。
- 输出：如果输入的所有位都是 0，输出为 1；否则，输出为 0。
问题简化：
- 这个问题本质上是一个比较问题，即判断所有的输入位是否为 0。
- 如果所有位都是 0，输出为 1；只要有一个输入位为 1，输出就为 0。

构建真值表

由于这是一个八位输入的电路，我们理论上需要构建一个包含 256 行的真值表（每个输入位可以为 0 或 1）。但是，实际上只有一行是我们关心的，即所有输入位都为 0 时输出为 1。其他所有情况输出都为 0。

我们可以直接跳过这些行，简化我们的分析。唯一需要关注的行是：

\( A_7 \)	\( A_6 \)	\( A_5 \)	\( A_4 \)	\( A_3 \)	\( A_2 \)	\( A_1 \)	\( A_0 \)	输出
0	0	0	0	0	0	0	0	1

子表达式构建

从真值表可以看到，唯一输出为 1 的条件是所有输入位都为 0。因此，我们的布尔表达式将是输入的每个位的非操作的“与”操作。

对于 \( A_0, A_1, A_2, …, A_7 \)，我们要计算所有位的“非”并进行与操作。
子表达式：
\[ \text{输出} = \neg A_7 \land \neg A_6 \land \neg A_5 \land \neg A_4 \land \neg A_3 \land \neg A_2 \land \neg A_1 \land \neg A_0 \] 这意味着，如果所有位都是 0，则所有的“非”结果都是 1，最终的与操作结果为 1。

画出电路图

反相器（NOT Gate）：
每个输入位 \( A_7, A_6, …, A_0 \) 都通过一个反相器（NOT Gate）进行取反操作。
与门（AND Gate）：
然后，所有反相器的输出通过多个与门进行两两组合，最终得到一个输出结果。

电路结构：
- 每个输入 \( A_7, A_6, …, A_0 \) 连接到一个反相器。
- 每两个反相器的输出连接到一个与门。由于与门一次只能处理两个输入，我们需要分层次地组合。
- 第一步，先两两组合 \( \neg A_7 \land \neg A_6 \)，\( \neg A_5 \land \neg A_4 \)，\( \neg A_3 \land \neg A_2 \)，\( \neg A_1 \land \neg A_0 \)。
- 第二步，将上述四个结果再两两组合：\( (\neg A_7 \land \neg A_6) \land (\neg A_5 \land \neg A_4) \)，\( (\neg A_3 \land \neg A_2) \land (\neg A_1 \land \neg A_0) \)。
- 最后一步，将第二步的结果组合，得到最终的输出。

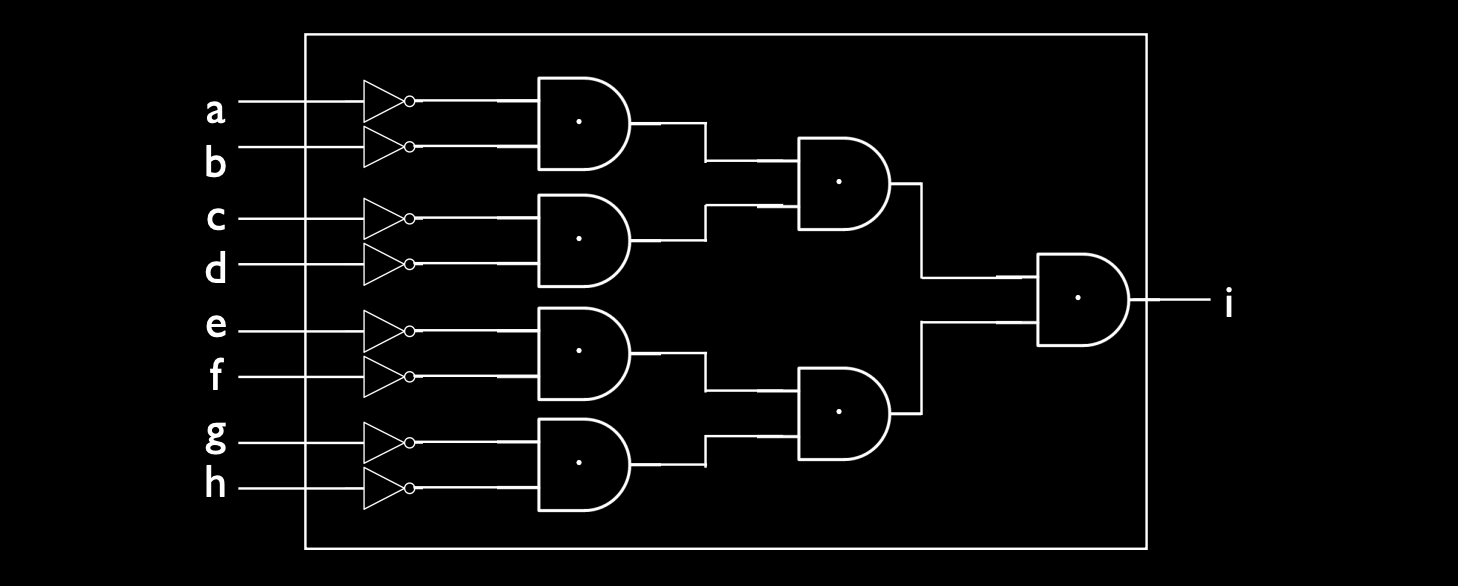
通过构建这个专用电路，我们可以快速判断一个八位二进制数是否为零。这个电路的效率非常高，因为它只依赖简单的逻辑门（NOT 和 AND），并且只需要针对所有输入位进行一次逻辑操作。这类专用电路在计算机体系结构中非常常见，因为它们能够加快常见操作的执行速度，节省处理器资源。

Karnaugh Map 介绍与电路优化

Karnaugh Map（卡诺图）是一种用于优化布尔表达式的图形化工具，帮助我们减少逻辑电路中使用的逻辑门数量，从而减少电路的复杂度。它重新排列了真值表，使得邻近的行或列只相差一个输入变量。这种布局使得我们可以更容易地找到可以组合的逻辑表达式，减少门的使用。

基本概念

假设我们有四个输入：\(A\)、\(B\)、\(C\)、\(D\)，这四个输入一共可以组合成 \(2^4 = 16\) 种不同的输入组合。我们的任务是根据某个特定的输出来优化这个电路。

传统的真值表方法

列出真值表：我们通常会列出所有可能的输入组合，并标记哪些组合的输出为 1。
构建布尔表达式：对于每个输出为 1 的行，我们会构建一个子表达式，使用 AND 和 NOT 来表示。
组合所有子表达式：最后，通过 OR 操作将所有子表达式组合起来，得到最终的表达式。

这个过程虽然有效，但对于复杂的电路来说，可能会产生大量的 AND 和 OR 操作，导致电路过于复杂，使用的门和晶体管数量过多。

为了简化电路设计，我们可以使用 Karnaugh Map 来减少逻辑门的数量。Karnaugh Map 通过重新排列输入组合，帮助我们找到可以合并的子表达式。

Karnaugh 图与真值表的构建和优化

根据给定的描述，我们要通过真值表和 Karnaugh 图（也称 K-图）优化电路设计。目标是通过最小化逻辑门的数量来减少所需的电路复杂性和资源消耗。在这个例子中，我们有四个输入变量（a、b、c、d）和一个输出变量（e），共有 16 种输入组合。

真值表

真值表列出了所有输入组合，并通过输出列展示了在每种组合下，输出 e 的值（即 0 或 1）。如下表所示：

a	b	c	d	e
0	0	0	0	0
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	1
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	1
1	1	0	0	1
1	1	0	1	1
1	1	1	0	1
1	1	1	1	0

Karnaugh 图

Karnaugh 图通过将真值表中的输入组合转换为二维矩阵形式，使相邻的逻辑项可视化，从而简化逻辑表达式。在这个 4 变量的情况下，Karnaugh 图是一个 4x4 的矩阵，其中每个单元格对应真值表中的一行输入。

表格结构：

水平轴 表示输入 a 和 b 的组合（00、01、11、10）。
垂直轴 表示输入 c 和 d 的组合（00、01、11、10）。

Karnaugh 图的填充：

根据真值表中的输出 e 值，Karnaugh 图被相应填充。每个单元格的值对应真值表中相应行的输出值。

ab\cd	00	01	11	10
00	0	0	0	0
01	0	0	0	1
11	1	1	0	1
10	1	1	1	1

简化逻辑表达式

通过观察 Karnaugh 图，我们可以找到相邻的输出为 “1” 的格子，并将这些格子合并为更简化的逻辑表达式。以下是一些关键步骤：

当 a = 1，b = 0，无论 c 和 d 是什么，输出都为 1。这可以简化为逻辑表达式：a̅b。
另一个情景：考虑 b=1b = 1b=1，c=1c = 1c=1，和 d=0d = 0d=0 时，输出也为 1，但这里 aaa 的值不影响输出，说明 aaa 在这种情况下是不相关的。
同样地，可以通过观察其他相邻的输出 “1”，进一步简化为更少的逻辑项。

Karnaugh 图优化逻辑电路

Karnaugh 图不仅提供了一种更直观的方式来处理和简化布尔逻辑表达式，而且还能有效减少实现特定逻辑功能所需的逻辑门数量。这种图的使用方法包括：

确定不相关变量：通过分析Karnaugh图中的输出格局，可以确定哪些变量在某些输出条件下是不相关的，从而可以在逻辑表达式中省略这些变量。
表达式合并：将多个相邻的 ‘1’ 合并为一个更简单的逻辑表达式，减少了所需的逻辑门。
重叠使用：在不同逻辑表达式间存在重叠时，可以进一步简化，因为同一个输出只要有一个表达式满足即可。

通过这种方式，可以生成包含较少变量的逻辑表达式，每个表达式涵盖更多的真值表行。这些简化的表达式不仅减少了逻辑设计的复杂性，还降低了实现电路时所需的物理空间和能耗。

通过使用 Karnaugh 图，设计者不仅能有效地减少所需的逻辑门数量，还能深入理解各个变量在布尔逻辑中的作用和相互关系。这种方法极大地提升了逻辑电路设计的效率和性能，是数字逻辑设计中不可或缺的工具之一。希望通过这段讲解，你能对计算机体系结构中的逻辑设计有更深的理解和应用能力。

总结

通过这次讲解，我们已经完成了从二进制数到布尔逻辑，再到电路设计的完整过程，通过Karnaugh Map优化电路。Karnaugh Map通过将真值表重新排列为二维矩阵的方式，帮助我们更直观地找到可以合并的布尔表达式，并减少电路中所需的逻辑门数量。通过这种方法，我们可以大大减少电路的复杂度和资源消耗。

要点：

从二进制数到布尔逻辑： 计算机的基本运算可以通过布尔代数实现，逻辑门（AND、OR、NOT等）是实现这些运算的基础组件。
真值表的构建： 真值表列出了所有可能的输入组合，并展示了相应的输出。这是设计电路的基础步骤。
Karnaugh Map（卡诺图）： 将真值表重组为二维矩阵，可以帮助我们识别哪些相邻的输出为1的格子可以简化为更少的布尔变量，从而减少电路中所需的逻辑门数量。
电路优化： 通过Karnaugh Map，我们能够在不影响输出的情况下合并多个表达式，减少使用的逻辑门数量，从而优化电路设计。

在整个过程中，我们看到了电路设计中的一系列优化方法。通过简化逻辑表达式，可以减少电路中逻辑门的数量，进而减少电路板上所需的晶体管数量。这使得我们能够在现代设备中集成更多功能，同时保持高效的计算能力。

这个流程展示了从基础的布尔逻辑运算，到复杂电路设计，再到优化过程的完整链条。理解这些基本概念不仅有助于理解现代计算机的工作原理，也为进一步学习计算机架构和硬件设计打下了坚实的基础。

这就是我们从基础布尔逻辑到电路优化的全部内容。希望你在后续的课程中能继续深入学习，探索更多计算机体系结构的奥秘！

a	b	c	d	e
0	0	0	0	0
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	1
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	1
1	1	0	0	1
1	1	0	1	1
1	1	1	0	1
1	1	1	1	0

a	b	c	d	e
0	0	0	0	0
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	1
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	1
1	1	0	0	1
1	1	0	1	1
1	1	1	0	1
1	1	1	1	0

a	b	c	d	e
0	0	0	0	0
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	1
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	1
1	1	0	0	1
1	1	0	1	1
1	1	1	0	1
1	1	1	1	0