Lecture 4. Higher-Order Functions

Textbook Ch. 1.6

本周的讨论与任务安排

1. 讨论课

• 本周三将进行课程的讨论课，内容包括一个讨论导览和一个教程。
• 讨论导览：与实验课一样，讨论课也有多场导览。时间表可以在课程的每周计划中找到。
  • 每天下午 2 点有两场讨论导览，其中一场专为编程经验较少的同学设计。如果你对课程不太熟悉，建议参加该场导览。
  • 导览之后的讨论教程时间从下午 3 点到晚上 11 点，适应不同时区的需求，晚上 6 点、7 点（针对编程经验少的同学）和 9 点也有导览。
  • 这些导览都会被录制，录制内容会上传至 Google Drive 文件夹中，方便无法参加的同学回看。

2. 讨论教程

• 请尽量参加讨论导览和讨论教程，如果你是最近加入课程的学生，确保已经在教程中注册。
• 如果尚未注册教程，可以访问 tutorials.cs61a.org 来寻找空闲的教程时段，并尽快报名。
• 本周教程将记录出勤，迟到 3 分钟以上将不被计入出勤，所以请务必准时参加。

3. 作业

• 作业 1（Homework 1）：本周四截止，请及时完成。
  • 不要共享代码或查看其他同学的代码，遇到问题时可以通过 Piazza 发帖，或者通过 office hours 获取帮助。
  • 本周三、四全天都有辅导时间，建议提前开始作业，以避免最后时刻排队等待帮助。

4. 实验课

• 本周五将举行实验课导览，由于下周一是节假日（周一不上课），但是 实验 2（Lab 2） 依然在周一截止。为了不耽误下周的任务进度，建议周五就完成实验。
  • 实验 2 只有 2 到 3 个题目，但如果不认真完成，后续任务会变得更难。
  • 最佳建议是周五完成实验 2，这样你可以专注于项目或在周末放松一下。

5. 考试准备

• 本周五下午 2 点 10 分将举行首次 考试准备课程，这是一次 Zoom 线上讲座，讲解助教们解决考试题目的策略，包括如何解决问题以及考试时遇到困难应该如何应对。
  • 该讲座为选修，不强制参加，内容也会被录制供之后观看。
  • 建议提早思考即将到来的期中考试，期中考试定于 9 月 14 日（星期一）举行。

6. 项目

• Hog 项目：这是本课程的第一个项目，将在下周五截止。
  • 项目类似于较长的作业，所有问题相互关联，最后会构建一个完整的应用程序。
  • 需要在下周二之前完成项目的第一部分 Phase 1，以获得检查点的 1 分奖励。强烈建议尽早开始项目，而不是等到最后一刻。
  • 第一阶段问题最具挑战性，完成之后进展会顺利很多。
• 合作伙伴：Hog 项目可以与同伴合作：
  • 合作时可以共享代码，仅需一位同学提交并在 ok.py 上标记合作伙伴即可。
  • 不建议分工完成项目，请通过 Zoom 共享屏幕，协同合作，确保双方都理解整个项目。

7. 期中考试（Midterm）

• 期中考试：定于 9 月 14 日（星期一），属于第 4 周的开端。期中考试会尽早安排，以便在退课截止日前（周三）为你提供反馈。
• 考试内容涵盖前两周的课程，重点包括高阶函数的概念与应用。本周的课程讲解（包括周五的讲座）对理解考试内容至关重要。

迭代与斐波那契数列的计算

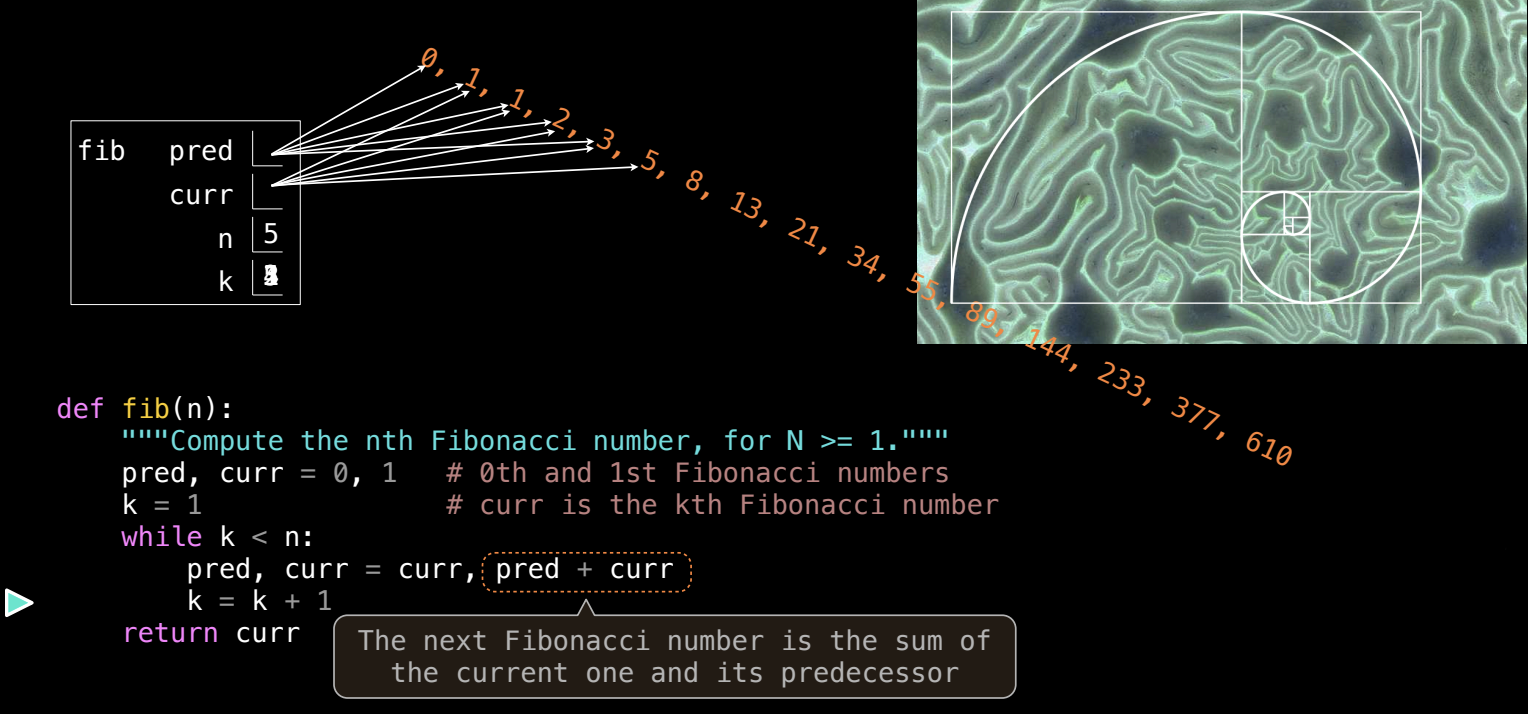
1. 斐波那契数列介绍

• 斐波那契数列（Fibonacci Sequence）是一个著名的数列，每一项都是前两项的和，数列从 0 和 1 开始。
• 例如：0, 1, 1, 2, 3, 5, 8, 13...
  • 第五个斐波那契数是 5（索引从 0 开始）。
• 斐波那契数列具有有趣的数学性质，如“黄金螺旋”，它在人类视觉中显得和谐，甚至在自然界中也常常被认为存在类似的形态。

2. 斐波那契数列的计算

• 我们可以使用 while 循环 来计算斐波那契数列中的某一项。
• 设计迭代函数时，关键是确定需要跟踪的信息。在斐波那契数列中，我们需要知道前两个数来计算下一个数。
  • 需要跟踪：
    1. 当前和前一个斐波那契数。
    2. 当前的位置索引 k。

def fib(n):
    pred, cur = 0, 1  # 初始值，第 0 和第 1 个斐波那契数
    k = 1  # 从第 1 项开始
    while k < n:  # 只要 k 小于 n，继续迭代
        pred, cur = cur, pred + cur  # 前一个数变为当前数，当前数变为前一个和当前的和
        k = k + 1  # 更新索引
    return cur  # 返回第 n 个斐波那契数

3. 环境图分析

• 当计算斐波那契数时，我们跟踪多个局部变量：pred、cur、n 和 k。
  • 初始值：pred=0, cur=1, k=1，代表第 1 个斐波那契数。
  • 每次循环更新 pred 和 cur，直到 k 等于 n，此时返回第 n 个斐波那契数。

4. 改进的斐波那契函数

• 我们可以改进初始值设置，使其能正确计算第 0 个斐波那契数。

def fib(n):
    pred, cur = 1, 0  # 初始值更改
    k = 0  # 从第 0 项开始
    while k < n:
        pred, cur = cur, pred + cur
        k = k + 1
    return cur

• 这段代码相比之前的版本，更能准确处理 n=0 的情况：
  • 当 n=0 时，cur 的值为 0，正确输出第 0 个斐波那契数。

函数设计与通用性概述

在这一部分，我们重点讨论如何设计更易于理解、适用广泛的函数。函数设计不仅影响代码的可读性，还决定了它们在不同场景中的应用效果。我们特别关注了斐波那契数列的函数设计，并介绍了如何通过使用 高阶函数 来表达更通用的计算模式。

函数的基本概念

• 函数的定义：
  • 域（Domain）：函数接受的所有可能输入的集合。
  • 值域（Range）：函数可能返回的所有值的集合。
  • 行为（Behavior）：输入与输出之间的关系。

例如：

def square(x):
 """Return X * X."""

• square(x) 函数：
  • 域：任何实数 x。
  • 值域：非负实数（大于等于零）。
  • 行为：返回输入值的平方。
• fibonacci(n) 函数：
  • 域：大于或等于 1 的整数 n。
  • 值域：斐波那契数。
  • 行为：返回第 n 个斐波那契数。

设计原则

• 一个函数应该只做一件事：每个函数应当有单一职责，过于复杂的函数会导致难以维护。
• 避免重复代码（DRY 原则）：一个功能实现一次即可，重复的代码应被抽象为函数。
• 定义通用函数：设计尽可能通用的函数，使其在更多场景中适用。

高阶函数的引入

• 高阶函数 是编程语言中的一个特性，允许我们将函数作为参数传递，并返回其他函数，从而实现更强的通用性和抽象。
• 通过高阶函数，可以定义出更为通用的计算模式。比如，我们通过将具体计算公式中的常量部分抽象出来，可以简化多个类似的几何面积计算公式。

示例：几何图形面积的通用计算

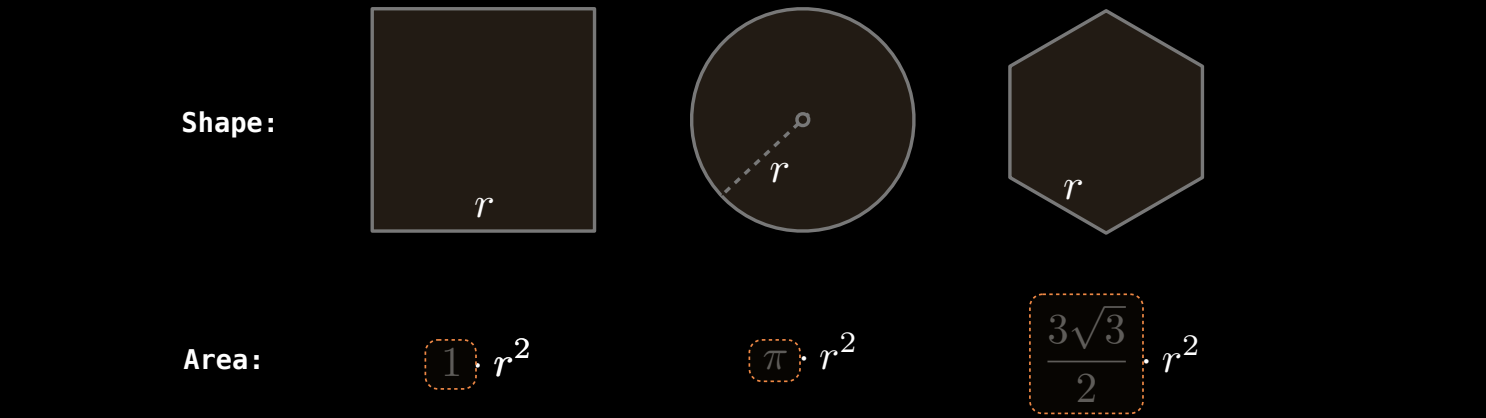
考虑三种几何图形（正方形、圆形、六边形）的面积计算：

# 定义正方形面积
def area_square(side_length):
    return side_length * side_length

# 定义圆的面积
from math import pi
def area_circle(radius):
    return pi * radius * radius

# 定义六边形的面积
from math import sqrt
def area_hexagon(side_length):
    return (3 * sqrt(3) / 2) * side_length * side_length

每个图形的面积公式都可以看作是某种 r^2 形式的扩展，其中常量部分因图形不同而有所不同。通过找出它们的共同结构（即 r^2），我们可以创建一个更加通用的函数。

高阶函数的应用

我们可以创建一个高阶函数，用于处理不同几何形状的面积计算：

def area_shape(r, constant):
    return constant * r * r

# 使用高阶函数计算正方形、圆形、六边形的面积
area_square = lambda r: area_shape(r, 1)
area_circle = lambda r: area_shape(r, pi)
area_hexagon = lambda r: area_shape(r, (3 * sqrt(3)) / 2)

# 计算面积
print(area_square(2))  # 输出：4
print(area_circle(2))  # 输出：12.566370614359172
print(area_hexagon(2)) # 输出：10.392304845413264

通过这个通用函数 area_shape，我们简化了不同图形面积计算的实现。每个具体形状只需传递其相应的常量系数，就可以调用同一个函数来完成计算。

定义高阶函数

我们可以将这些重复的计算过程进行抽象，以实现更加通用的代码设计。通过识别出不同函数之间的共同结构，特别是像对自然数求和、立方求和等数学公式中的共同部分，我们可以通过定义高阶函数来简化这些过程。

问题的共同结构

在求和过程中，不同公式的核心是：我们对某个序列中的项进行某种操作（例如，求和、求立方和等），而唯一的区别是对每个项的具体操作不同。例如：

• 自然数求和公式：$1 + 2 + 3 + \dots + n$
• 立方和公式：$1^3 + 2^3 + 3^3 + \dots + n^3$
• 更复杂的公式也遵循类似的模式，唯一不同的就是我们对每个项应用的函数不同。

因此，我们可以编写一个通用的高阶函数，它能够接受一个“操作”作为参数，并将该操作应用到每个项上。

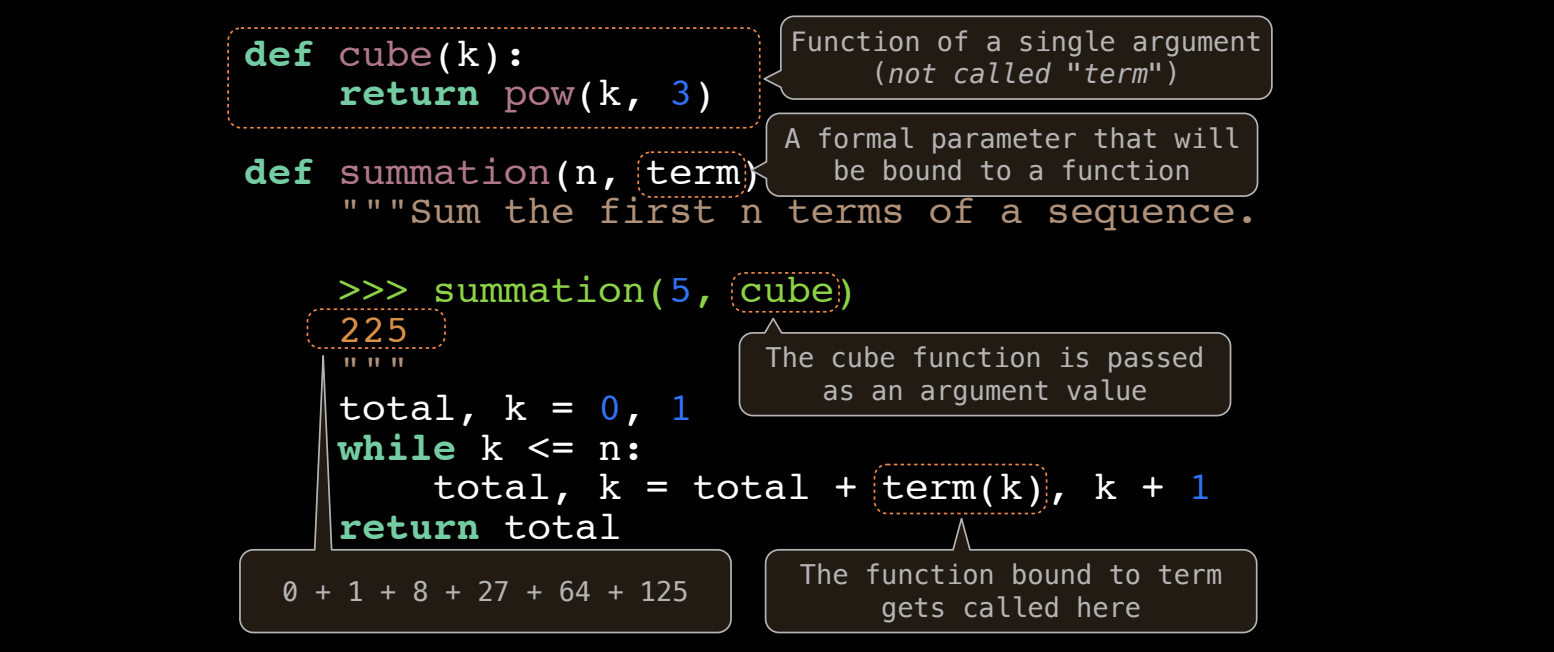
通用求和函数

我们将这种通用的计算过程抽象为一个高阶函数，通过传入不同的操作来计算不同的求和结果：

# 定义通用的求和函数
def summation(n, term):
    """将从1到n的每一项应用term函数并求和"""
    total = 0
    k = 1
    while k <= n:
        total += term(k)
        k += 1
    return total

# 定义求自然数的函数
def identity(k):
    return k

# 定义求立方的函数
def cube(k):
    return k * k * k

# 定义复杂的公式函数
def complex_term(k):
    return 8 / ((4 * k - 3) * (4 * k - 1))

# 使用通用求和函数
print(summation(5, identity))  # 1 + 2 + 3 + 4 + 5 = 15
print(summation(5, cube))      # 1^3 + 2^3 + 3^3 + 4^3 + 5^3 = 225
print(summation(5, complex_term))  # 计算复杂公式的前5项和

高阶函数的好处

通过这样的高阶函数设计，我们可以：

• 避免代码重复：不需要为每种求和公式写多个几乎相同的函数，只需要定义不同的项函数（如 identity, cube, complex_term），然后使用通用的 summation 函数。
• 提高代码的可读性与维护性：高阶函数让代码更具通用性和扩展性，便于在未来添加更多种类的公式。

实际运行结果

通过通用函数 summation，我们可以轻松计算不同的求和公式。例如：

print(summation(5, identity))  # 输出: 15
print(summation(5, cube))      # 输出: 225
print(summation(5, complex_term))  # 输出: 一个接近 3.04 的值

这样，我们将不同问题的相似结构抽象了出来，并通过高阶函数实现了通用的解决方案。这不仅让代码更加简洁和通用，也使得我们更容易添加和修改不同的计算逻辑。

计算逼近 π 的序列

用 summation 来计算复杂的数学序列。例如，计算一个逐渐收敛到 π 的序列：

# 定义逼近π的项的函数
def pi_term(k):
    return 8 / ((4 * k - 3) * (4 * k - 1))

# 计算前1000000项的和
approx_pi = summation(1000000, pi_term)
print(approx_pi)  # 输出: 3.141592...

通过这种方式，我们可以看到如何将通用的计算过程抽象为一个函数，而具体的计算方式则通过传递不同的函数来实现。

返回函数的函数（函数生成器）

除了传递函数作为参数外，我们还可以定义一个函数，它返回另一个函数。例如，定义一个可以生成加法函数的函数：

高阶函数 make_adder 示例

高阶函数是可以接收函数作为参数或返回函数的函数。在示例中，我们定义了一个高阶函数 make_adder，它返回一个用于加法操作的函数：

def make_adder(n):
    """返回一个函数，该函数将 n 与它的输入相加"""
    def adder(k):
        return k + n
    return adder

使用示例：

add_three = make_adder(3)
print(add_three(4))  # 输出: 7

make_adder(3) 返回了一个函数 adder(k)，该函数将 k 与 3 相加。因此，当我们调用 add_three(4) 时，计算结果为 7。

函数作为返回值

make_adder 是一个典型的高阶函数，它返回了一个新的函数。返回的函数可以“记住”外层函数的参数：

add_five = make_adder(5)
print(add_five(10))  # 输出: 15

在这个例子中，add_five 记住了 n=5，然后将它与传递的参数相加。

函数调用表达式作为操作符表达式（Call Expressions as Operator Expressions）

在 Python 中，函数调用是一个重要的表达式类型，它由操作符（operator）和操作数（operand）组成。这里，操作符是一个返回函数的表达式，而操作数是传递给该函数的参数。函数调用表达式首先会对操作符和操作数进行求值，然后执行该函数。

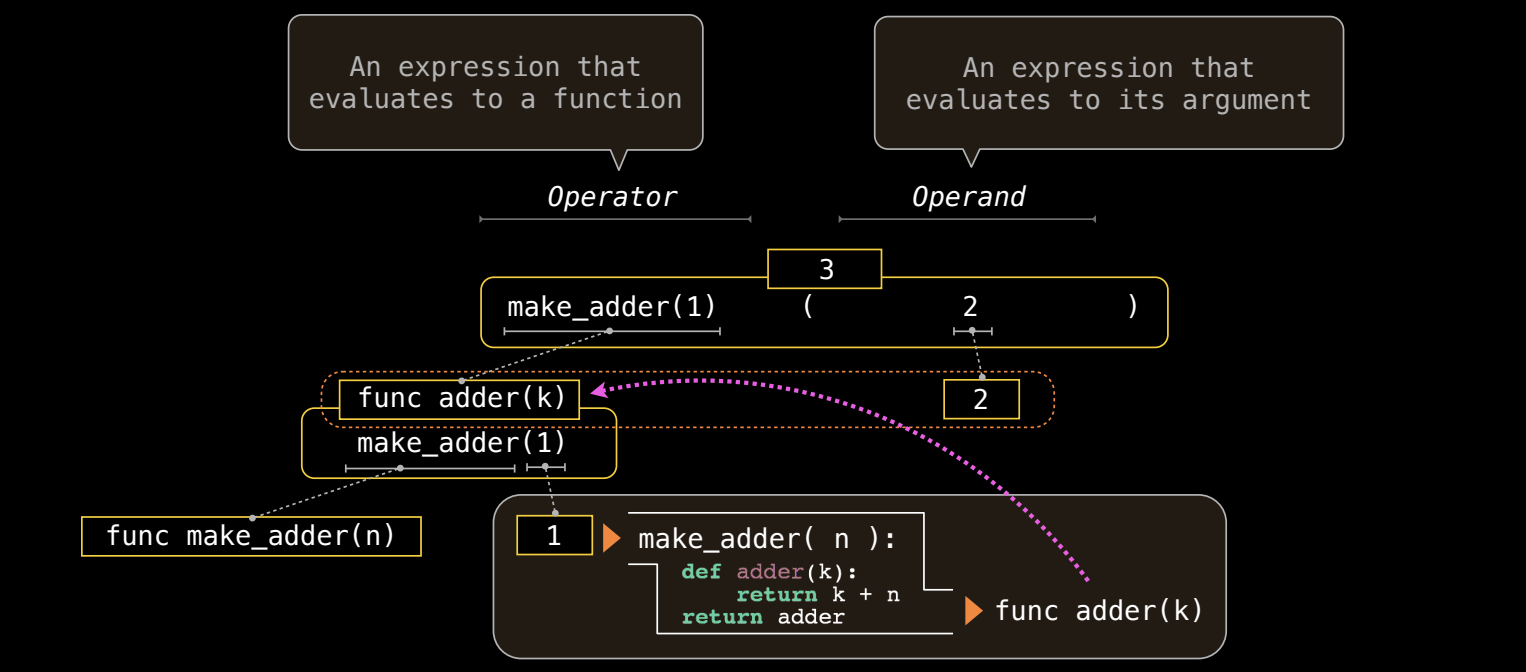
操作符与操作数

1. 操作符：是一个求值为函数的表达式。在图示中，make_adder(1) 是一个操作符，它求值为一个名为 adder 的函数，该函数的参数是 k。这个 adder 函数通过闭包机制捕获了外部的 n 值（这里为 1）。

2. 操作数：是传递给操作符（函数）的参数。在图中，2 是操作数，它将被传递给 adder(k) 函数，作为参数 k 的值。

函数调用的过程解析

图示中展示了以下代码的执行过程：

def make_adder(n):
    def adder(k):
        return k + n
    return adder

make_adder(1)(2)

1. 定义 make_adder 函数：make_adder(n) 定义了一个外部函数，该函数接收参数 n，并在其内部定义了另一个函数 adder(k)。adder 函数接收参数 k，并返回 k + n 的结果。通过 return adder，make_adder 返回 adder 函数，使得可以通过 make_adder 来生成自定义的加法函数。

2. 调用 make_adder(1)：调用 make_adder(1) 时，参数 n 被绑定为 1，并返回 adder 函数。在这个阶段，adder 函数被创建，它捕获了 n = 1 的值。

3. 执行 adder(2)：接着，返回的 adder 函数被立即调用，并传入参数 2。此时，adder 函数的 k 绑定到 2，并计算 k + n，即 2 + 1，返回结果 3。

闭包（Closure）

在这个例子中，adder 函数是一个闭包。闭包是指在函数定义时捕获了它所在的外部作用域中的变量（即 n），即使在外部作用域结束后，这些变量依然可以被函数使用。因此，当 adder 函数被返回并调用时，它依然能够访问 make_adder 调用时的 n 的值。

Lambda 表达式

Lambda 表达式是一种简洁定义匿名函数的方式。你可以在一行中定义一个函数，而不必使用 def 语句。

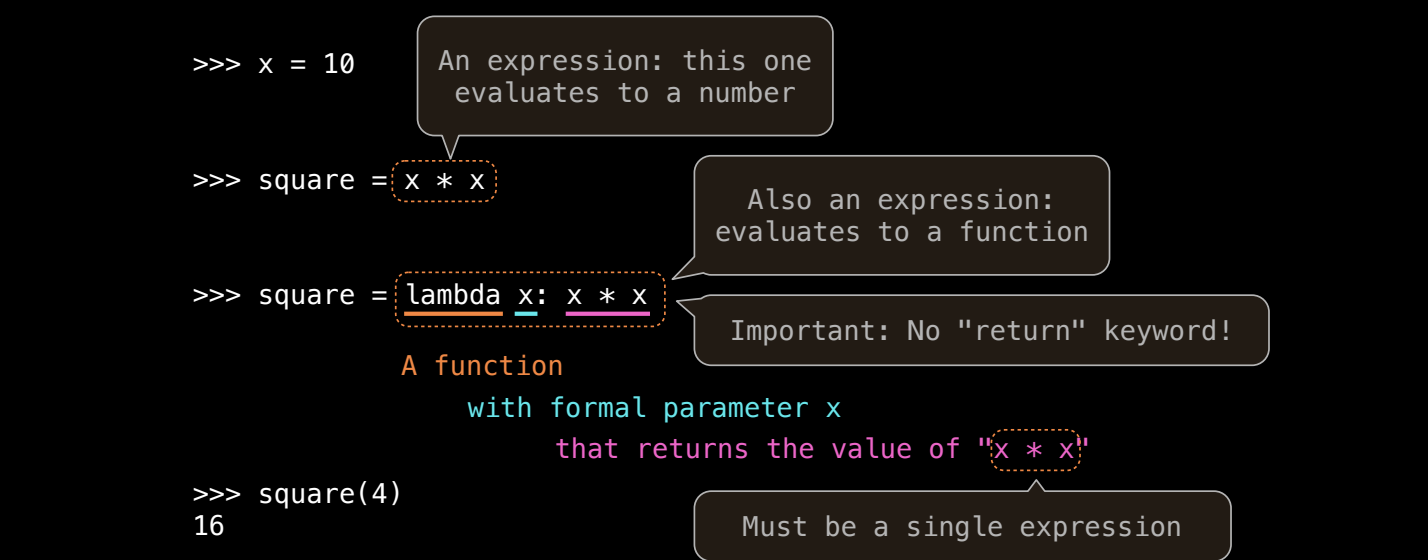
例子：

square = lambda x: x * x
print(square(5))  # 输出: 25

在这里，lambda x: x * x 创建了一个函数，该函数接收参数 x 并返回 x 的平方。

更复杂的应用：

我们还可以在函数中使用 lambda 表达式，例如高阶函数 summation：

def summation(n, term):
    """对前 n 个自然数应用 term 函数并求和"""
    total = 0
    k = 1
    while k <= n:
        total += term(k)
        k += 1
    return total

# 使用 lambda 表达式传递自定义的函数
print(summation(5, lambda x: x * x))  # 输出: 55，求前 5 个数的平方和

在这个例子中，lambda x: x * x 作为参数传递给 summation 函数，计算了前 5 个数的平方和。

高阶函数的意义

高阶函数在编程中具有以下重要意义：

1. 减少代码重复：通过将重复的逻辑抽象为高阶函数，可以避免代码冗余。
2. 提高代码的灵活性：你可以根据不同的需求传递不同的函数，从而复用相同的逻辑框架。
3. 增强可读性：通过合理命名和抽象，代码逻辑变得更容易理解和维护。

例子：计算 Pi 的序列求和

以下是如何使用高阶函数和 lambda 表达式来求解一个逼近 π 的数列求和的示例：

def pi_term(k):
    """返回用于计算 pi 逼近值的项"""
    return 8 / ((4 * k - 3) * (4 * k - 1))

# 使用 summation 函数来逼近 π 值
approx_pi = summation(1000000, pi_term)
print(approx_pi)  # 输出: 3.141592...

在这个例子中，我们定义了 pi_term 函数来计算序列中的每一项，并使用高阶函数 summation 来完成总和计算。

Lambda 表达式与 Def 语句

在 Python 中，定义函数有两种常见方式：使用 lambda 表达式和 def 语句。两者都能创建具有相同功能的函数，但它们的实现方式和表现存在一些细微的差异。

Lambda 表达式

Lambda 表达式是一种简洁的函数定义方式，通常用于定义简单的、一次性使用的函数。其语法为：

lambda 参数: 表达式

Def 语句

Def 语句是更传统的函数定义方式，它允许定义更复杂的函数，并且函数具有明确的名称。语法为：

def 函数名(参数):
    函数体

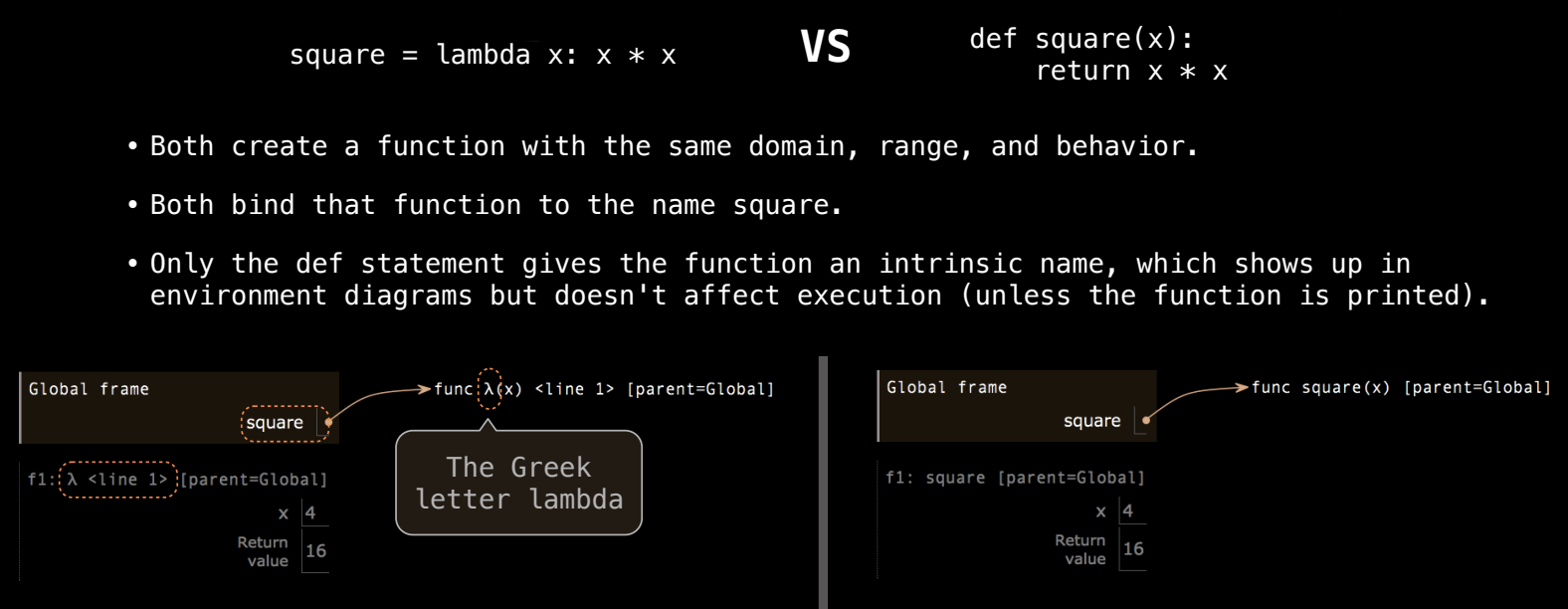
在这个例子中，我们通过 Lambda 表达式和 def 语句创建了相同的函数，但这两者之间有一些关键差异。我们来详细分析这些差异，并理解它们在 Python 中的使用。

首先，Lambda 表达式是用于创建匿名函数的，它允许我们在一行中定义简单的函数。Lambda 表达式的语法如下：

square = lambda x: x * x

这行代码创建了一个接收参数 x 并返回 x * x 的匿名函数，并将其绑定到 square 这个变量。你可以像调用普通函数一样使用这个 Lambda 表达式：

print(square(4))  # 输出 16

与此相对，def 语句是 Python 中最常用的定义函数的方式。你可以通过 def 语句为函数提供一个明确的名称，并允许定义更复杂的逻辑。如下是相同的函数使用 def 语句的版本：

def square(x):
    return x * x

当你定义并调用这个函数时，它与使用 Lambda 表达式定义的函数表现几乎一致：

print(square(4))  # 输出 16

区别

虽然这两种方法在功能上类似，但它们有一些细微的区别：

1. 名称绑定：

   • Lambda 表达式创建的函数是匿名的，只有在通过赋值语句绑定到一个变量（如 square）时才有名字。
   • def 语句创建的函数本身就有一个名字，它是定义函数时直接赋予的。

2. 函数名的显示：

   • 当你查看 Lambda 表达式创建的函数时，Python 只会显示 lambda，而不会显示你绑定的变量名：

     print(square)  # 输出 <function <lambda> at 0x...>
     

   • 使用 def 语句创建的函数会显示定义时赋予的函数名：

     print(square)  # 输出 <function square at 0x...>
     

3. 功能限制：

   • Lambda 表达式只能包含一个简单的表达式，不能包含复杂的语句（如循环或多行逻辑）。它主要用于定义简单的、一次性的函数。
   • def 语句没有这样的限制，可以用于定义复杂的函数逻辑。

4. 可读性和惯例：

   • 虽然 Lambda 表达式在某些场合非常简洁，但是在 Python 中，更多情况下使用 def 语句是更为常见的做法，因为它更具可读性，尤其在处理复杂的逻辑时。

环境图的区别

在环境图中，Lambda 表达式和 def 语句生成的函数都有不同的表示方式。在 Lambda 表达式创建的函数中，我们使用希腊字母 λ 来表示它，因为它没有明确的函数名。而 def 语句创建的函数则显示其定义时的函数名。

例如，以下代码：

square = lambda x: x * x
result = square(4)

生成的环境图中，square 绑定到一个 Lambda 表达式，调用该函数时会生成一个新的帧，而帧中只会显示 λ 而不是函数名 square。

相反，使用 def 定义函数时：

def square(x):
    return x * x
result = square(4)

生成的环境图会显示 square 函数名，并在调用时同样生成一个新帧，帧中显示的是 square 函数名。

返回语句 Return

接下来探讨如何通过返回语句和 while 循环来控制函数的执行，以及返回语句在函数中的作用和实现。

首先，返回语句的核心功能是结束函数的执行并返回一个值。在执行函数时，Python 进入新的环境，在执行完函数体后，遇到返回语句时，函数执行结束，返回值会传递回原来的调用环境。因此，一旦在函数体中遇到返回语句，后续的代码将不再执行。

示例 1：数字逆序打印直到找到目标数字

我们可以编写一个函数，它从一个非负整数 n 的最后一位开始，按逆序打印各位数字，直到找到某个指定的目标数字 d。例如，如果 n 是 34567，目标数字是 5，函数会打印 7、6、5，然后停止。

def print_reverse_until_d(n, d):
    """Print the final digits of N in reverse order until D is found.

    >>> end(34567, 5)
    7
    6
    5
    """
    while n > 0:
        last_digit = n % 10  # 提取最后一位
        print(last_digit)  # 打印最后一位
        if last_digit == d:  # 找到目标数字
            return  # 结束函数
        n = n // 10  # 去掉最后一位

在这个例子中，while 循环会不断处理 n，直到找到目标数字 d。一旦找到 d，return 语句结束函数的执行，不再继续循环或执行后续的代码。

示例 2：无限循环与条件返回

接下来，我们编写一个函数 search，它接受一个函数 f 作为参数，不断从 0 开始尝试不同的整数 x，直到找到一个使得 f(x) 为 True 的整数。

def search(f):
    x = 0
    while True:  # 无限循环
        if f(x):  # 如果 f(x) 为真值
            return x  # 返回 x，结束循环
        x += 1  # 否则继续尝试下一个 x

这个函数的 while True 是一个无限循环，只有当 f(x) 为真时，才通过 return 结束函数。这样的设计可以用于查找满足特定条件的最小整数值。

示例 3：平方根的反函数

我们可以利用 search 函数来构建一个简单的平方根计算器。通过定义一个平方函数，然后反转它来得到平方根函数。

def square(x):
    return x * x

def inverse(f):
    def g(y):
        return search(lambda x: f(x) == y)  # 查找使 f(x) == y 的最小 x
    return g

sqrt = inverse(square)

# 测试平方根函数
print(sqrt(16))  # 输出 4
print(sqrt(256))  # 输出 16

在这个例子中，inverse 函数通过 search 来找到一个数 x，使得 f(x) 等于给定的 y，从而间接计算平方根。这样的方法是通过尝试多个可能的值来反转函数的行为。

平方根的反函数

在这个例子中，我们通过函数的反转来实现一个简单的平方根计算器。这个过程通过定义一个平方函数，并利用二分查找（search）来反向推导平方根。

1. 函数反转的概念

所谓函数反转，是指我们给定一个函数 f(x)，然后通过查找或计算，找到一个 x 使得 f(x) 等于某个值 y，即 f(x) = y。在这个例子中，我们定义了一个求平方的函数 square(x)，接着使用 inverse 函数来计算 square 的反函数——也就是平方根函数。

2. 核心函数解析

def square(x):
    return x * x

这个函数简单地返回输入 x 的平方。我们可以通过它来计算任何一个数的平方。例如：

• square(4) 会返回 16，因为 ( 4^2 = 16 )。
• square(16) 会返回 256，因为 ( 16^2 = 256 )。

接下来我们希望实现反向操作，即已知 square(x) = y，求 x。

def inverse(f):
    def g(y):
        return search(lambda x: f(x) == y)  # 查找使 f(x) == y 的最小 x
    return g

inverse 函数的设计非常巧妙：

• 它接受一个函数 f，并返回一个新的函数 g。
• 新的函数 g(y) 会调用 search 函数，查找一个 x，使得 f(x) 等于传入的参数 y。

换句话说，inverse 函数可以接受任意一个可逆函数，并返回其反函数。例如，如果我们传递 square 作为参数，inverse(square) 将返回一个可以计算平方根的函数。

3. search 函数的角色

通过遍历或者二分查找等方法，寻找使得 f(x) == y 成立的 x。在这个例子中， search 函数通过遍历从可能的 x 值中查找满足条件的最小 x。

4. 使用 inverse 函数构建平方根函数

sqrt = inverse(square)

这里我们使用 inverse(square) 构建了 sqrt 函数。sqrt 实际上是 g(y) 的别名，它通过 search 来查找满足 square(x) == y 的最小 x。

5. 示例运行

print(sqrt(16))  # 输出 4
print(sqrt(256))  # 输出 16

对于 sqrt(16)，我们希望找到一个 x 使得 square(x) == 16。通过 search 函数，二分查找会得出 x = 4，因为 ( 4^2 = 16 )。

同样地，sqrt(256) 会返回 16，因为 ( 16^2 = 256 )。

6. inverse 方法的优点

使用 inverse 来构建反函数的主要优点在于：

• 通用性：inverse 是一个通用的函数反转工具，不仅适用于 square，还可以用于任何可反转的单调函数。
• 动态查找：通过 search，我们不需要提前知道函数的解析式。只要能计算函数 f(x)，就可以通过查找得到 f 的反函数。

7. inverse 的局限性

尽管 inverse 方法很灵活，但它也有一定的局限性：

• 效率：如果 search 函数的实现是通过暴力查找，效率可能不高。在查找范围较大时，使用如二分查找等优化方法是必要的。
• 精度：查找函数的精度也很重要。如果我们不对查找进行限制，可能会得到近似的解而不是精确解。因此，search 函数通常会有一个精度控制参数。

总结

这个例子展示了如何使用 inverse 函数和查找方法来动态构建平方根函数。通过将 square 传递给 inverse，我们得到了 sqrt 函数，它能够通过反转平方函数来计算平方根。

这种方法虽然简单，但非常灵活，可以应用于任何能够通过查找反向求解的函数。

控制语句 Control

在 Python 中，条件语句 if 和函数调用的主要区别在于评估顺序。函数调用的规则是先评估所有参数，再执行函数体，而 if 语句则根据条件，只执行符合条件的分支。因此，当涉及可能会出错的表达式时（例如负数的平方根），if 语句可以避免出错，而函数调用不能。以下是进一步的解释和具体例子。

条件语句的执行方式

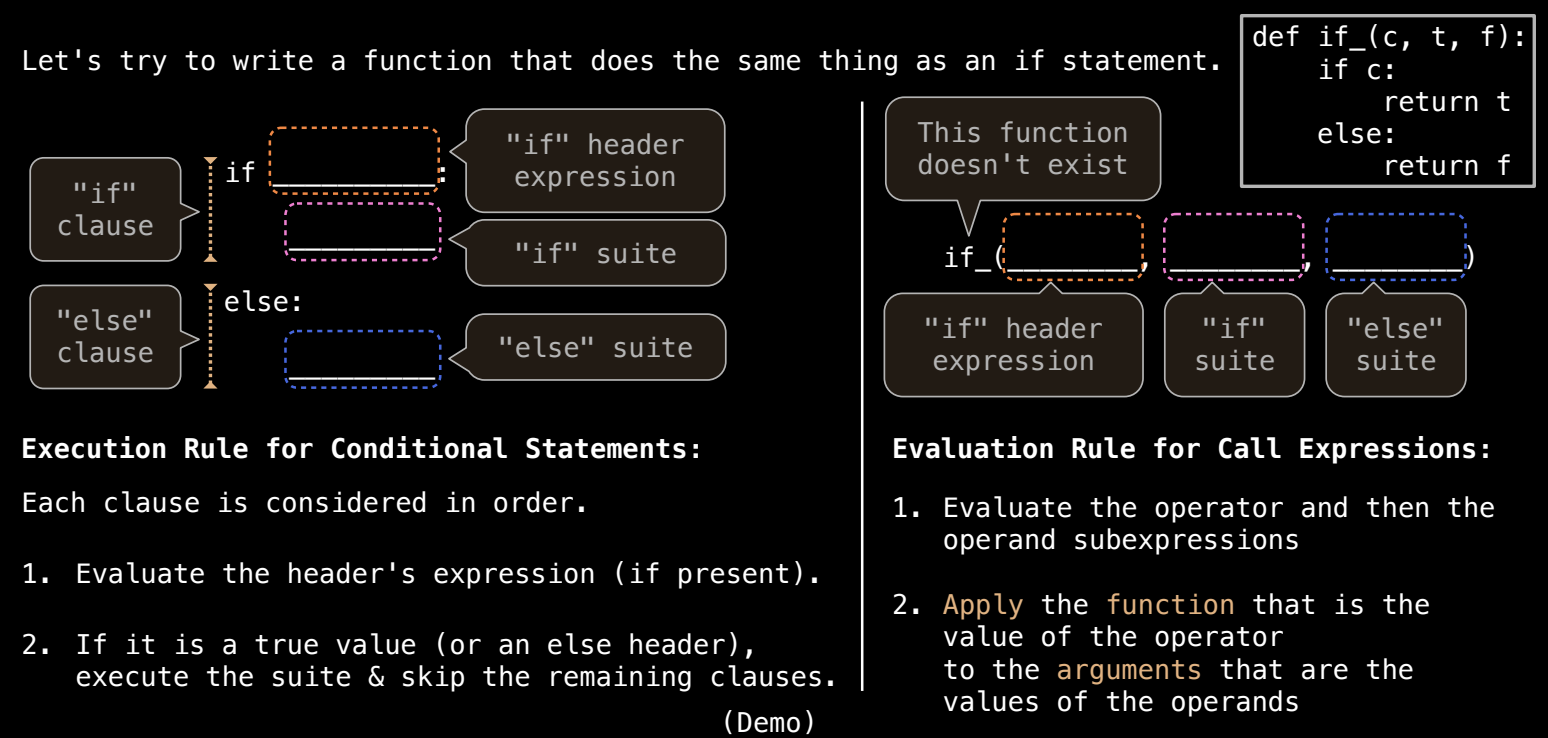
在条件语句中，只有当条件为 True 时，才会执行与之对应的代码块。例如：

import math

def real_sqrt(x):
    if x >= 0:
        return math.sqrt(x)  # 只当 x >= 0 时执行
    else:
        return 0  # 否则返回 0

在这个例子中，只有当 x >= 0 时才会调用 math.sqrt(x)，否则会返回 0，而不会尝试计算负数的平方根。这样就避免了计算负数平方根时出现的错误。

print(real_sqrt(4))  # 输出: 2.0
print(real_sqrt(-4))  # 输出: 0

即使你传入 -4，因为条件 x >= 0 为 False，程序不会尝试计算 math.sqrt(-4)，而是直接返回 0。

函数调用的评估顺序

但是，如果我们尝试用一个函数来模拟 if 语句的行为，这样的函数会先评估所有参数，而不是根据条件只评估一个。例如：

def if_function(condition, true_result, false_result):
    if condition:
        return true_result
    else:
        return false_result

使用这个函数来替代 if 语句：

import math

def real_sqrt(x):
    return if_function(x >= 0, math.sqrt(x), 0)

当我们执行这段代码时，math.sqrt(x) 会在传递给 if_function 之前被立即计算，而不管 x 是什么：

print(real_sqrt(4))  # 正常输出: 2.0
print(real_sqrt(-4))  # 发生错误: ValueError: math domain error

如你所见，当 x 为 -4 时，程序依然尝试计算 math.sqrt(-4)，尽管条件 x >= 0 为 False，因为函数的参数在调用之前就已经被评估了。这与 if 语句的行为不同，if 语句会根据条件判断来选择执行哪一部分代码，而不会提前评估所有表达式。

总的来说，if 语句的优势在于它具有短路行为：当条件为 True 或 False 时，只执行对应的分支，不会评估其他分支中的表达式。而在函数调用中，所有参数都会被先评估，这可能导致不必要的计算或错误。

这个例子展示了 Python 中条件语句与函数调用在评估顺序上的不同，尤其是在可能引发错误的情况下，条件语句可以有效地避免无效表达式的执行。

逻辑运算符的短路求值

Python 提供了逻辑运算符 and 和 or 的短路求值机制，可以用来避免不必要的计算。例如：

def has_big_square_root(x):
    return x > 0 and math.sqrt(x) > 10

在这个例子中，如果 x 小于等于 0，Python 不会继续计算 math.sqrt(x)，从而避免了对负数开平方的错误：

print(has_big_square_root(1))       # 输出: False
print(has_big_square_root(1000))    # 输出: True
print(has_big_square_root(-1000))   # 输出: False

条件表达式

Python 还提供了一种简洁的条件表达式，可以嵌入到更复杂的表达式中，形式为 x if condition else y：

x = 0
result = abs(1/x if x != 0 else 0)
print(result)  # 输出: 0

在这个例子中，如果 x == 0，条件表达式会返回 0，而不会评估 1 / x，从而避免零除错误。