Lecture 22. Efficiency (optional)
Announcements
作业与项目的更新
- 本周实验:截止日期为周二。
- 蚂蚁项目:将于周五截止,但需要在周二前完成项目的第一和第二阶段。如果在周四之前提交整个项目,可获得提前提交的加分,建议尽量在周四前提交。
- 作业5:已发布,截止日期是下周一。这份作业是即将到来的期中考试的一个很好的复习材料。
- 下周实验:唯一必做的部分是完成作业5,实验中会有一些可选问题,可以帮助你为期中考试做额外的练习,但这些问题不是必做的。
- 匿名问卷:这是填写第八周匿名问卷的最后机会,我们非常感谢您的反馈。
期中考试提醒
- 期中考试二:将于下周三晚上7点(太平洋时间)举行,考试形式和风格与期中考试一相似,涵盖的内容截至上周五的讲座。
- 今天的讲座(关于效率的内容):不会出现在考试、作业或实验中,这只是一个本学期的选修话题,但在未来的 61B 课程中会深入学习效率相关的内容。因此,如果你将来会学习 61B,今天的讲座是一个很好的预习。
树递归与 Fibonacci 数列
之前我们介绍了如何使用树递归计算 Fibonacci 数列。树递归是指递归的每个分支可以生成多个递归调用,像一棵树一样展开。以下是 Fibonacci 数列的递归定义:
- Fibonacci 序列:
F(0) = 0,F(1) = 1, 其余的值为前两个值的和,即F(n) = F(n-1) + F(n-2)。
Measuring Efficiency 效率分析
在计算 Fibonacci 数列时,树递归的效率非常低,因为许多中间结果会被重复计算。例如,计算 F(5) 需要计算 F(4) 和 F(3),而 F(4) 又需要再次计算 F(3),这种重复计算导致时间复杂度呈指数增长。
通过计算调用次数,我们可以了解程序的执行效率。以下是 Fibonacci 递归的一个简单实现,并通过修饰器记录函数调用的次数:
递归实现 Fibonacci 并计算调用次数:
def fib(n):
if n == 0 or n == 1:
return n
return fib(n - 2) + fib(n - 1)
def count_calls(f):
def counted(n):
counted.call_count += 1
return f(n)
counted.call_count = 0
return counted
fib = count_calls(fib)
fib(5)
print(f"Fib(5) 被调用了 {fib.call_count} 次") # 输出: Fib(5) 被调用了 15 次
随着 n 的增加,调用次数呈指数增长。例如,计算 F(30) 需要 2.69 百万次递归调用。显然,随着输入的增大,这种实现方式的效率非常低。
记忆化(Memoization)
为了提高效率,可以使用记忆化技术。记忆化是一种缓存技术,用于存储已经计算过的结果,从而避免重复计算。这可以极大地减少递归调用的次数,使得时间复杂度从指数级降低到线性级。
记忆化的基本思想
记忆化是一种通过缓存已计算结果来提高函数执行效率的技术。它适用于纯函数,即函数在相同输入下总是返回相同结果,且不依赖外部状态或产生副作用。
当使用记忆化技术时,函数的每次调用都会首先检查缓存是否已经存储了该输入的结果。如果已存储,则直接返回缓存的结果;如果没有存储,则计算结果并将其存储在缓存中,以备后续使用。
记忆化 fib 函数的实现
def memo(f):
cache = {} # 创建一个缓存字典
def memoized(n):
if n not in cache: # 如果 n 不在缓存中
cache[n] = f(n) # 计算结果并存入缓存
return cache[n] # 返回缓存的结果
return memoized
- 缓存字典(cache):存储函数的输入和对应的结果。输入作为键,结果作为值。
- 缓存检查:在计算函数结果之前,先检查输入是否已经在缓存中。如果在缓存中,则直接返回缓存值;否则,计算并将结果存储在缓存中。
使用记忆化加速 Fibonacci 计算
将 fib 函数与记忆化结合,实现快速计算 Fibonacci 数列。
@memo
def fib(n):
if n == 0 or n == 1:
return n
return fib(n - 2) + fib(n - 1)
- 基本情况:当
n为 0 或 1 时,直接返回n。 - 递归计算:对于其他情况,递归调用
fib(n - 2)和fib(n - 1),并将结果相加。
示例:
print(fib(30)) # 输出: 832040,几乎瞬间计算出结果
通过记忆化,fib(30) 仅需计算每个 Fibonacci 数列项一次,而不会重复计算,从而显著减少了递归调用次数。
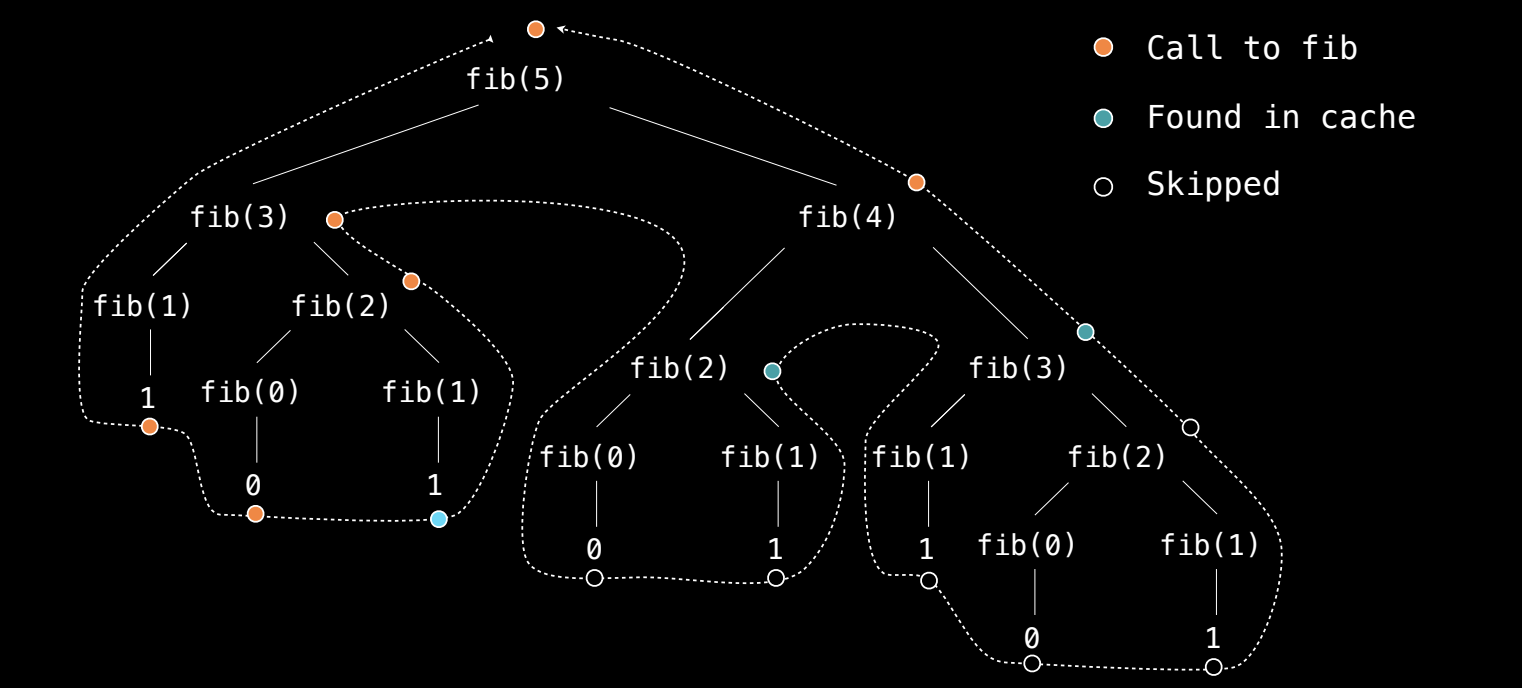
调用次数分析
为了进一步分析调用次数,我们可以为 fib 函数添加计数功能,了解递归调用的实际次数。
def count_calls(f):
def counted(n):
counted.call_count += 1
return f(n)
counted.call_count = 0
return counted
fib = count_calls(fib) # 包装 fib 函数以计数
在使用记忆化的情况下,计算 Fibonacci 数列时,每个数值只会被计算一次,随后如果再次需要该数值,将直接从缓存中读取。这使得 Fibonacci 数列的计算时间从指数级缩减为线性级。
调用次数的分析结果
- 缓存命中:当函数再次遇到相同的输入时,直接从缓存中读取,避免了递归调用。这大大减少了递归的深度和计算次数。
- 实际调用次数:例如,计算
fib(30)时,虽然 Fibonacci 数列的第 30 项需要递归调用很多次,但在使用记忆化后,fib实际只被调用了 31 次(对应 0 到 30 之间的数值)。
@装饰器的使用及记忆化fib函数的实现在 Python 中,
@是装饰器语法糖,用于简化函数装饰器(decorator)的使用。装饰器是一个高阶函数,它接收一个函数作为参数,并返回一个新的函数或修改后的函数。装饰器通常用于在不改变原始函数代码的前提下,为该函数添加额外的功能。记忆化
fib函数的实现我们通过装饰器为
fib函数实现记忆化(也叫缓存)功能,来加速 Fibonacci 数列的计算。记忆化是指在递归过程中保存已经计算过的值,以避免重复计算。1.
memo装饰器的实现def memo(f): cache = {} # 创建一个缓存字典 def memoized(n): if n not in cache: # 如果 n 不在缓存中 cache[n] = f(n) # 计算结果并存入缓存 return cache[n] # 返回缓存的结果 return memoized
- 缓存字典(cache):
cache是一个字典,保存已经计算过的f(n)的结果。字典的键是函数的输入参数n,值是对应的函数计算结果f(n)。- 缓存检查:在
memoized(n)中,先检查n是否在cache字典中。如果不在,说明还没计算过,就调用函数f(n)进行计算,并将结果存入cache;如果已经计算过,就直接返回缓存的值。- 返回装饰后的函数:
memoized(n)是实际执行函数计算的内部函数。memo装饰器的作用是将f函数包装成memoized,从而对原始函数f添加缓存功能。2.
fib函数与记忆化结合@memo def fib(n): if n == 0 or n == 1: return n return fib(n - 2) + fib(n - 1)
@memo装饰器:@memo的作用是将fib函数传递给memo装饰器。在函数定义时,@memo相当于执行fib = memo(fib),这意味着fib函数现在是被装饰后的函数,它被包装成了带有缓存功能的memoized函数。- 基本情况:当
n为 0 或 1 时,fib(n)直接返回n。- 递归调用:对于大于 1 的
n,fib函数递归调用fib(n - 2)和fib(n - 1)并将结果相加。这时,由于使用了@memo装饰器,fib(n)会缓存已经计算过的结果,避免重复递归计算。3. 装饰器的实际运行过程
- 首次调用时:当
fib(5)被调用时,首先检查5是否在缓存cache中。如果不在,则调用原始的fib(5),同时递归调用fib(4)和fib(3)。这些递归调用都会存储其结果到cache中。- 重复调用时:如果再次调用
fib(5),程序会直接从缓存中取出结果,而不再进行递归计算,从而显著提高计算效率。记忆化的优点
- 时间复杂度降低:没有记忆化的
fib函数的时间复杂度是指数级的O(2^n),因为每次递归都要重复计算相同的子问题。通过记忆化,时间复杂度降低为O(n),每个fib(n)的值只会计算一次并存入缓存。- 减少重复计算:记忆化缓存了已经计算的结果,使得递归过程中不必重复计算同样的
n。
高效的幂运算(Exponentiation)
除了 Fibonacci 计算,记忆化也可以应用于其他递归计算,例如幂运算。计算一个数 b 的 n 次方(b^n)是编程中常见的问题,尤其是在数学、物理模拟、加密算法等领域中广泛使用。对于较大的 n,直接进行逐次乘法的算法效率较低,因此我们可以通过优化来加速这个过程。
基本指数运算问题:
目标是计算 b^n,其中 b 是底数,n 是指数。最直接的递归方法是:
- 当
n == 0时,返回1,因为任何数的 0 次方等于 1。 - 否则,返回
b * b^(n-1),即通过将n逐步减少,递归地计算b^n。
递归实现幂运算(效率较低)
传统的递归幂运算函数每次只减少 n 的值1,因此时间复杂度较高。
def exp(b, n):
if n == 0:
return 1
return b * exp(b, n - 1)
这种实现的时间复杂度为 O(n),即每次递归只减少 n 的值1,因此倍数增加 n 时,计算时间也倍增。
高效幂运算:使用平方加速(Exponentiation by Squaring)
我们可以通过指数平方法来提高幂运算的效率。利用二分递归的思想:如果我们知道 b 的一半次方的结果,就可以通过少量的额外运算获得完整的结果。例如,如果 n 是偶数,我们可以先计算 b 的 n/2 次方,然后将结果平方,而不需要每次都递减 1。
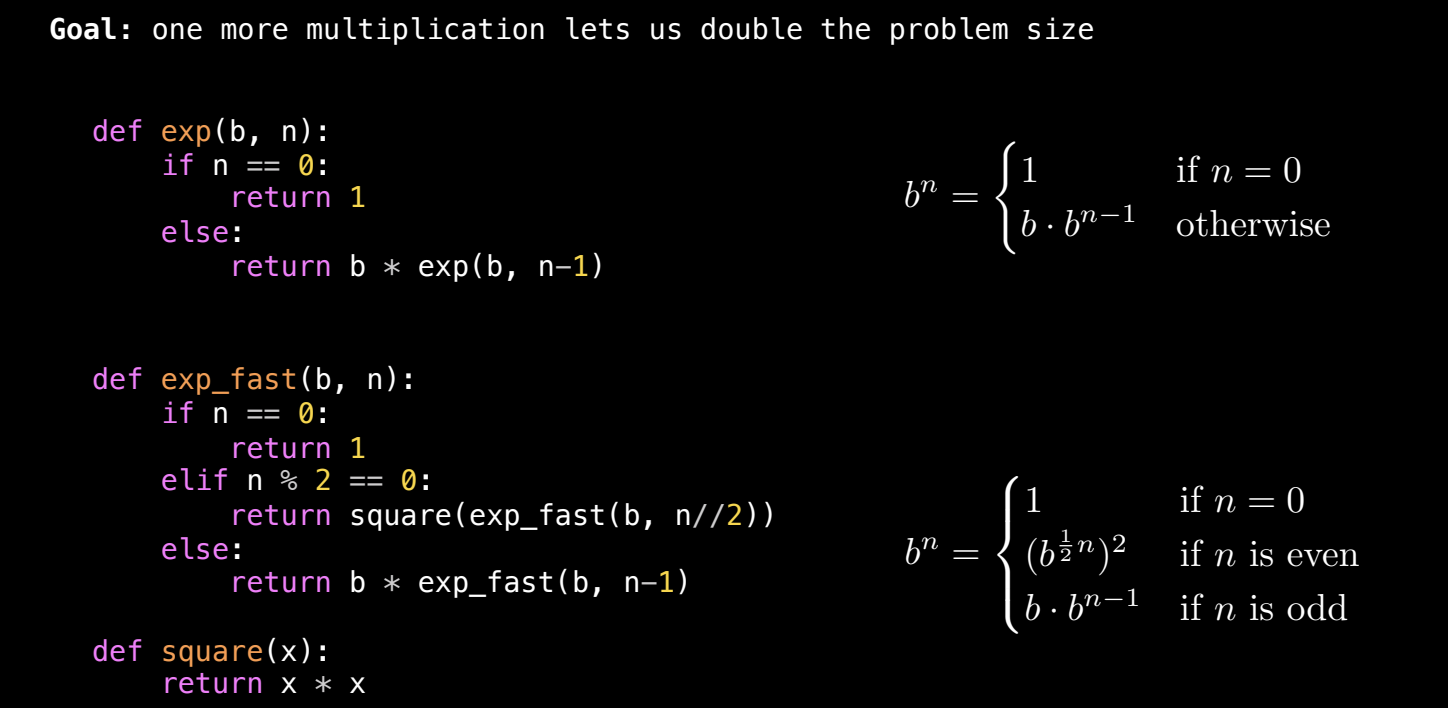
优化思想:
- 当
n为偶数时,b^n可以转换为(b^(n/2))^2,这减少了递归调用的次数。 - 当
n为奇数时,仍然需要多乘以一次b,然后继续递归计算b^(n-1)。
def fast_exp(b, n):
if n == 0:
return 1
elif n % 2 == 0:
half = fast_exp(b, n // 2)
return half * half
else:
return b * fast_exp(b, n - 1)
- 偶数情况:如果
n是偶数,则递归调用fast_exp(b, n // 2),并将结果平方。 - 奇数情况:如果
n是奇数,则递归调用fast_exp(b, n - 1),并乘以基数b。
示例:
print(fast_exp(2, 10)) # 输出: 1024
时间复杂度对比:
- 线性时间(O(n)):
- 普通递归方法每次减少
n的值 1,因此计算2^n需要进行n次乘法操作。 - 每当输入
n加倍,运算时间也加倍,因此时间复杂度为 O(n)。
- 普通递归方法每次减少
- 对数时间(O(log n)):
- 使用指数平方法,每次递归将
n减半,因此时间复杂度为 O(log n)。 - 当
n加倍时,运算时间只增加一个常量倍数。
- 使用指数平方法,每次递归将
时间复杂度的概念
时间复杂度用于描述算法的性能,衡量输入规模(n)对运行时间的影响。以下是几种常见的时间复杂度:
线性时间(O(n)):
- 算法执行时间随着输入大小呈线性增长。例如,遍历一个长度为
n的列表,时间复杂度为 O(n)。
对数时间(O(log n)):
- 每次递归调用将问题规模减半,时间复杂度为 O(log n)。指数平方法就是一个例子。
二次时间(O(n^2)):
- 对于每对输入进行比较,执行时间随输入大小呈平方增长。例如,嵌套的双重循环会产生 O(n^2) 的时间复杂度。
- 示例:计算两个列表的重叠项。
def overlap(a, b):
count = 0
for x in a:
for y in b:
if x == y:
count += 1
return count
- 示例:计算
[3, 5, 7, 6]和[4, 5, 6, 5]的重叠项,时间复杂度为 O(n^2),即对每个a的元素,检查b中的所有元素。
指数时间(O(2^n)):
- 当问题的规模每次递归都成倍增加时,执行时间呈指数级增长。树递归是典型的例子,如未经优化的 Fibonacci 数列递归计算。

时间复杂度曲线的分析
- 线性增长:时间复杂度为 O(n) 的函数,其时间随输入大小成正比增长。若输入大小翻倍,执行时间也翻倍。
- 对数增长:时间复杂度为 O(log n) 的函数,其时间随输入大小增加而缓慢增长。每次输入翻倍时,执行时间仅增加一个常量倍数。
- 二次增长:时间复杂度为 O(n^2) 的函数,其时间随输入大小呈平方增长。输入大小翻倍,执行时间会增长为原来的四倍。
- 指数增长:时间复杂度为 O(2^n) 的函数,其时间随输入大小呈指数级增长,性能极差。
如何通过优化改进时间复杂度
- 记忆化(Memoization) 可以将一些递归函数的时间复杂度从指数级降低为线性级,通过缓存已经计算过的结果避免重复计算。
- 指数平方法(Exponentiation by Squaring) 可以将指数运算的时间复杂度从 O(n) 降低到 O(log n),每次将问题规模减半,大大提高了效率。
大 O 记号和大 Θ 记号的区别
在计算机科学中,我们经常使用 大 O 记号(Big O Notation) 和 大 Θ 记号(Big Theta Notation) 来描述算法的时间复杂度和增长行为。这些记号有助于我们理解程序在处理不同输入规模时的表现。
大 Θ 记号(Big Theta Notation)
- 大 Θ 描述了算法运行时间的确切增长率,即它既是算法的上界也是下界。
- 形式:
Θ(f(n))表示算法在最坏、最好、平均情况下都表现为f(n)的增长。- 例如:
Θ(n^2)表示该算法的时间复杂度在所有情况下都是二次增长。
- 例如:
大 O 记号(Big O Notation)
- 大 O 主要用于描述算法的上界,即在最坏情况下,算法的执行时间不会超过某个量级。
- 形式:
O(f(n))表示在最坏情况下,算法的时间复杂度不超过f(n)。- 例如:
O(n^2)表示算法的最坏情况下表现为二次增长,但它可能在某些情况下表现得更好,比如O(n)或O(log n)。
- 例如:
常见增长类型及表示
- 常数时间(Constant Time):
- 大 Θ:
Θ(1) - 大 O:
O(1) - 描述:无论输入大小,操作的执行时间是固定的,例如哈希表查找。
- 大 Θ:
- 对数时间(Logarithmic Time):
- 大 Θ:
Θ(log n) - 大 O:
O(log n) - 描述:输入每次增加一倍,时间只增加一个常量倍数。常见于二分查找算法。
- 大 Θ:
- 线性时间(Linear Time):
- 大 Θ:
Θ(n) - 大 O:
O(n) - 描述:执行时间与输入规模成正比。常见于遍历列表。
- 大 Θ:
- 二次时间(Quadratic Time):
- 大 Θ:
Θ(n^2) - 大 O:
O(n^2) - 描述:时间复杂度随输入大小平方增长。常见于嵌套循环。
- 大 Θ:
- 指数时间(Exponential Time):
- 大 Θ:
Θ(2^n) - 大 O:
O(2^n) - 描述:时间复杂度呈指数增长,通常效率非常低。
- 大 Θ:
空间复杂度和内存管理
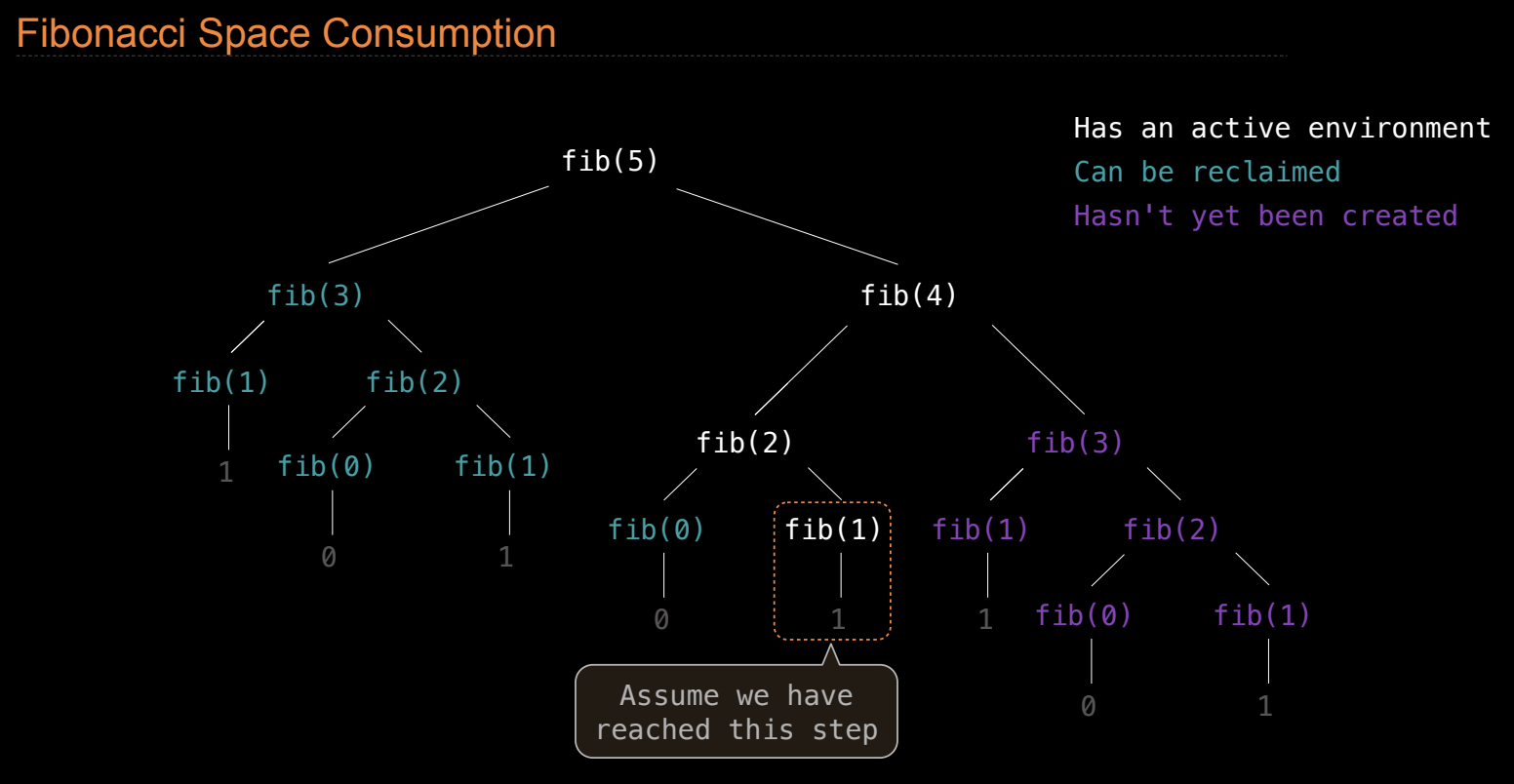
空间复杂度描述了程序执行时所消耗的内存资源。除了时间复杂度外,了解程序在运行时占用的内存(即栈帧数量)也很重要。
栈帧(Frames)和空间消耗
每次函数调用都会创建一个新的栈帧,这个栈帧存储了函数的局部变量、参数以及其他相关数据。在递归调用中,函数会嵌套调用,导致多个栈帧被占用,直到所有递归函数返回为止。
- 栈帧的空间:栈帧占用内存,当递归调用层数较多时,会占用大量内存。计算 Fibonacci 数列时,每层递归都创建新的栈帧,直到递归完全展开。
示例:计算 Fibonacci 数列时的栈帧
例如,在递归计算 Fibonacci 数列时,每个递归调用都创建一个栈帧。栈帧的最大数量与递归深度相关。
通过定义一个统计栈帧的函数,我们可以测量 Fibonacci 函数在执行过程中打开的栈帧数量:
def count_frames(f):
def counted(n):
counted.open_count += 1
counted.max_count = max(counted.max_count, counted.open_count)
result = f(n)
counted.open_count -= 1
return result
counted.open_count = 0
counted.max_count = 0
return counted
我们可以使用该函数包装 Fibonacci 函数,测量执行时最大打开的栈帧数量:
@count_frames
def fib(n):
if n == 0 or n == 1:
return n
return fib(n - 1) + fib(n - 2)
fib(20)
print(fib.max_count) # 输出: 20,表示最多打开了 20 个栈帧
- 结果分析:在递归计算 Fibonacci(20) 时,最多打开了 20 个栈帧,这意味着递归深度达到了 20 层。
内存管理和垃圾回收
Python 通过自动垃圾回收(Garbage Collection)机制回收不再使用的内存。当递归函数返回时,Python 会自动清除已返回的栈帧,以便释放内存资源。
空间复杂度的优化
在递归算法中,空间消耗主要由栈帧决定。优化空间复杂度的常见方法包括:
- 尾递归优化:某些编程语言支持尾递归优化,减少栈帧的占用。
- 迭代替代递归:通过将递归改为迭代,可以避免深度递归导致的栈溢出问题。