Lecture 8. Recursion

Textbook Ch. 1.7

公告

期中考试一的评分正在进行中，结果很快就会发布。我们尽量保持评分一致性，但可能会有错误。如果你觉得某部分的分数与评分标准不符，可以提交重新评分申请，截止日期为周一。

本周将进行讨论三，讨论的起始代码已经发布，讨论的工作表也会很快发布。本周的教程问题较少，因为刚刚进行了期中考试，目的是让大家有时间反思并讨论课程进展。如果你希望向导师询问学习建议，或与教程中的同学组建学习小组，可以利用这个时间。合作学习是提高成绩的有效方式，而这门课程的目标就是不断进步。如果期中考试一的表现不如预期，不用担心，因为我们还在课程初期。期中考试二的权重比期中考试一更大，期末考试的权重更大。大部分课程分数尚未决定，所以请专注于后续的提升。

课程进展

本周没有考试准备环节，因为你刚刚参加过考试。相反，我们将在周五下午2:10至3:00举行一次问答环节，可以向讲师提问。课程外的学生组织计算机科学导师（CSM）也为本课程提供支持，他们增加了一些小组导师环节，学生反馈通常非常积极。如果有兴趣，可以报名参加这些额外的学习机会。

Hog策略比赛将于周一结束，目前尚未开放提交表单，但可以继续完善最终策略。记住，最终策略必须是一个确定性的函数，即策略的行为应完全基于玩家分数，而不是随机的。同时，在额外回合中使用八面骰子而不是六面骰子。

时间安排

本周没有任何作业或项目的截止日期，因为你已经花费了大量时间准备期中考试。下一个作业将在周五发布，下周将有一个新的项目。

今天我们将进入课程的一个全新主题——递归（Recursion），这是课程中最有趣但也最具挑战性的部分之一。

image-20240911111002618

递归简介

递归是函数的一种形式，函数体内部调用自身，可以是直接调用，也可以是间接调用。递归不仅在计算机科学中出现，还广泛存在于艺术、自然和数学中。例如，谢尔宾斯基三角形是由三个更小的谢尔宾斯基三角形组成的，递归地嵌套。

我们将以一个简单的例子来介绍递归：数字求和。例如，2025这个数字，其各位数之和为 2 + 0 + 2 + 5 = 9。这种操作有很多实际应用，比如判断一个数是否能被9整除，其判断方法就是看其数字和是否能被9整除。此外，数字求和也可以用于错误检测。

  • 在实际应用中，信用卡校验码就是通过类似的算法计算的，虽然它并不是简单的数字求和。校验码用于检测人们在输入信用卡号码时是否发生了错误。

    image-20240911111139784

递归实现数字求和

我们通过一个递归函数来实现数字求和，而不使用循环（while）语句。这涉及将数字分割为最后一位和除去最后一位的部分。

分割函数 split

我们定义一个辅助函数 split 来分割数字：

  • 除去最后一位：通过 n // 10 获得。
  • 最后一位：通过 n % 10 获得。

例如，对于数字2025：

  • 除去最后一位的部分为 202
  • 最后一位为 5

接下来，我们将递归地对数字进行求和。

递归函数 sum_digits

我们用递归来计算数字各位之和：

  1. 基准情况：当 n < 10 时，n 是个位数，直接返回该数字。
  2. 递归情况：将 n 分割为除去最后一位的部分和最后一位，然后递归地计算除去最后一位部分的数字和，再加上最后一位。

代码实现 

def split(n):
    """Split positive n into all but its last digit and its last digit."""
    return n // 10, n % 10

def sum_digits(n):
    """Return the sum of the digits of positive integer n."""
    if n < 10:
        return n  # 基准情况：个位数直接返回
    else:
        all_but_last, last = split(n)  # 分割数字
        return sum_digits(all_but_last) + last  # 递归调用

示例运行 

print(sum_digits(2025))  # 输出 9

image-20240911112040223

递归函数的结构

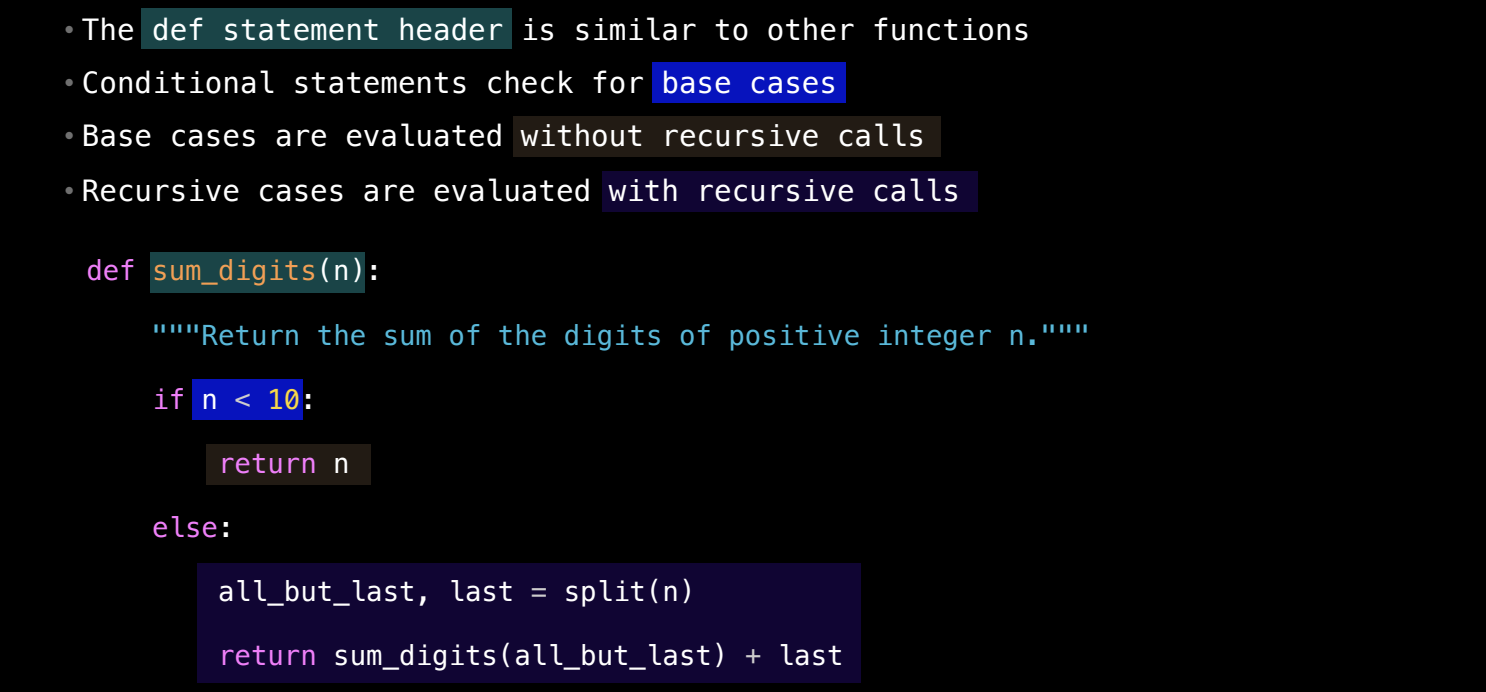
递归函数一般由两部分组成：

  1. 基准情况：解决最简单的问题，不需要递归调用。例如，数字是个位数时，直接返回该数字。
  2. 递归情况：将问题简化成一个更小的相同问题，然后递归调用函数自身。例如，将 2025 拆解为 202 和 5，递归计算 202 的数字和。

环境图中的递归

为了更好地理解递归，我们可以借助环境图。环境图展示了每次函数调用时的参数、返回值和执行过程。每次递归调用时，Python 会创建一个新的环境来处理当前的参数和变量，直到递归到达基准情况。

阶乘函数示例

我们可以通过阶乘函数来更深入理解递归的调用过程。阶乘的定义是 n! = n * (n-1)!，例如 3! = 3 * 2 * 1 = 6。

代码实现

def factorial(n):
    if n == 0:
        return 1  # 0 的阶乘为 1
    else:
        return n * factorial(n - 1)  # 递归调用

当我们调用 factorial(3) 时：

  1. factorial(3) 调用了 factorial(2)
  2. factorial(2) 调用了 factorial(1)
  3. factorial(1) 调用了 factorial(0)
  4. factorial(0) 返回 1，然后每一层递归逐步返回计算结果。

环境图解析

在递归中，每一次函数调用都会创建一个新的帧（frame），用于存储当前函数的参数和局部变量。帧通过环境图表示，帮助我们跟踪每一次递归调用。

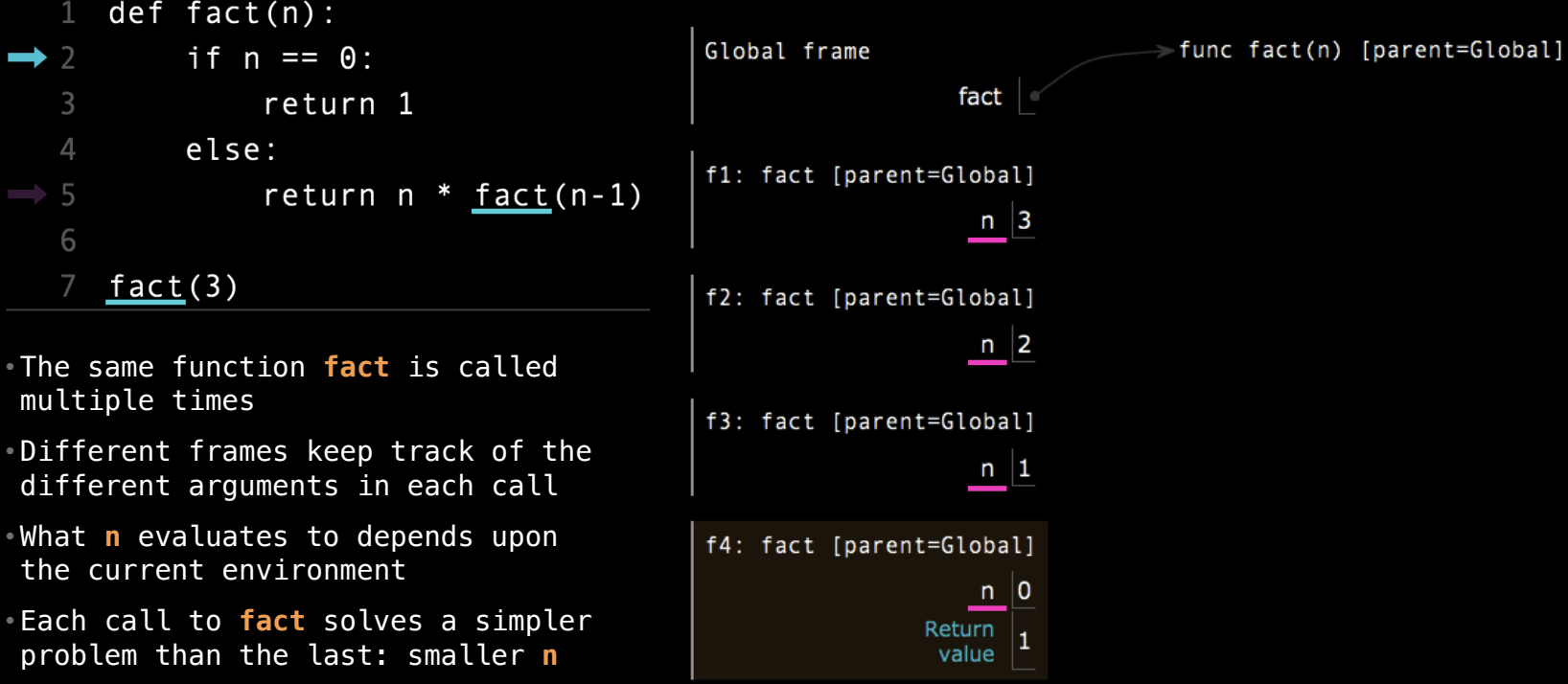
image-20240911112725958

例如，factorial(3) 的调用过程如下：

  1. factorial(3) 创建第一个帧，传入 n=3。
  2. factorial(2) 创建第二个帧，传入 n=2。
  3. factorial(1) 创建第三个帧，传入 n=1。
  4. factorial(0) 创建第四个帧，返回 1。

然后依次返回结果：

  • factorial(1) 返回 1 * 1 = 1
  • factorial(2) 返回 2 * 1 = 2
  • factorial(3) 返回 3 * 2 = 6

最终，factorial(3) 返回 6。

递归与迭代的对比

递归是一种简洁的方式来描述问题，例如阶乘的递归定义。但同样的逻辑可以使用迭代来实现。

image-20240911112815034

迭代实现阶乘

def factorial_iterative(n):
    total = 1
    k = 1
    while k <= n:
        total *= k
        k += 1
    return total

在这个迭代版本中，我们通过 while 循环逐步将 1 到 n 的值相乘，最终返回 n!。

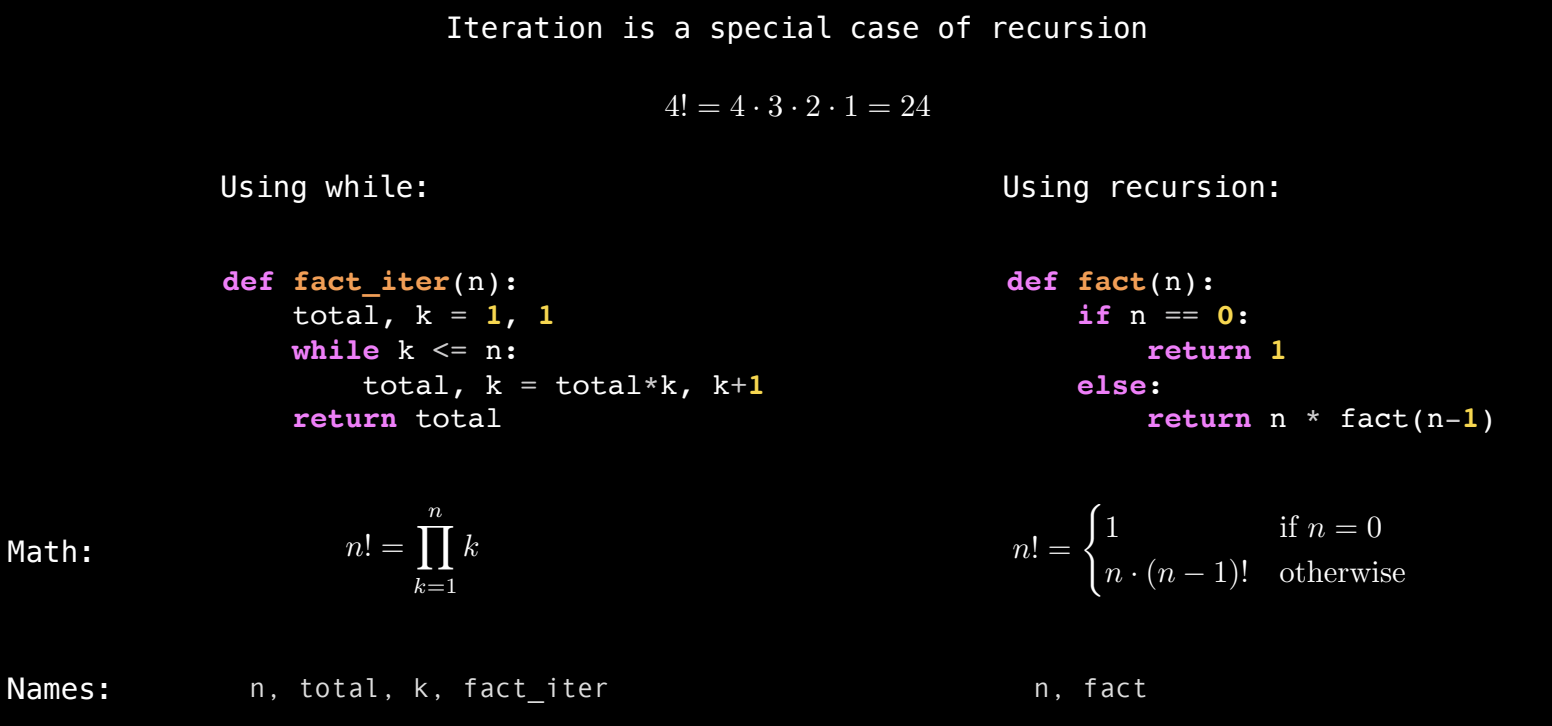
在计算阶乘时，递归和迭代提供了两种不同的实现方式。递归的表达更为简洁和直观，特别是当我们思考问题的定义时，递归可以直接映射到数学公式：

  • 递归定义：n! = n * (n-1)!，其中 n! = 1 当 n=0 时。
  • 迭代实现：通过一个 while 循环，每次累乘当前值，直到遍历完所有数字。

递归实现简单明了，计算过程中只需跟踪递归调用。而迭代实现需要额外的变量来存储计算结果，并且要手动控制循环的进展。在阶乘问题中，递归的简洁性更为突出。

递归正确性验证：递归的飞跃信念（Leap of Faith）

当我们写递归函数时，验证其正确性可以通过以下步骤进行：

  1. 验证基准情况：基准情况是递归的基础，必须是简单且正确的。例如，factorial(0) 应该返回 1。
  2. 递归假设：假设递归调用返回正确的结果，不深入探讨递归的具体实现，而是将其作为一个已知的正确行为。
  3. 验证整体函数：在递归假设下，验证递归调用能否解决当前问题。例如，对于 factorial(4)，我们可以假设 factorial(3) 是正确的，然后验证 4 * factorial(3) 是否正确计算了 4!。

Mutual Recursion（互相递归）

互相递归指的是两个或多个函数互相调用的现象。例如，函数 A 调用函数 B，而函数 B 又调用函数 A。

Luhn 算法：信用卡校验和

Luhn 算法用于计算信用卡号的校验和，以检测输入的有效性。该算法通过以下步骤计算：

  1. 从右侧开始，每隔一位数字进行加倍。
  2. 如果加倍后的结果大于 9，则将其各位数字相加。
  3. 将所有数字相加，计算和。
  4. 如果结果是 10 的倍数，则信用卡号有效。

image-20240911113114098

示例：对于信用卡号 138743，计算步骤如下：

  • 3 保持不变
  • 4 加倍为 8
  • 7 保持不变
  • 8 加倍为 16，数字和为 1 + 6 = 7
  • 3 保持不变
  • 1 加倍为 2

最后，将所有结果相加：2 + 3 + 7 + 7 + 8 + 3 = 30。由于 30 是 10 的倍数，因此信用卡号有效。

互相递归的实现

在 Luhn 算法中，我们可以用互相递归来实现校验和的计算：

  1. luhn_sum：计算不加倍的位数字之和。
  2. luhn_sum_double：计算加倍位数字之和，并将结果加回到总和中。
def luhn_sum(n):
    if n < 10:
        return n
    else:
        all_but_last, last = split(n)
        return luhn_sum_double(all_but_last) + last

def luhn_sum_double(n):
    if n < 10:
        return sum_digits(2 * n)
    else:
        all_but_last, last = split(n)
        return luhn_sum(all_but_last) + sum_digits(2 * last)

在这个实现中，luhn_sum 和 luhn_sum_double 互相调用，实现了互相递归。

递归提供了简洁且直观的实现方式，特别是在问题本身具有递归结构时，例如阶乘计算。互相递归则适用于更复杂的情况，如 Luhn 算法。通过递归和互相递归，我们可以有效解决复杂问题，同时保持代码的简洁性和可读性。

递归与迭代的转化

递归到迭代的转化

递归函数的逻辑可以转化为迭代形式，关键在于通过 while 循环保持递归状态的更新。例如，之前的数字求和函数可以通过迭代实现。

递归版数字求和

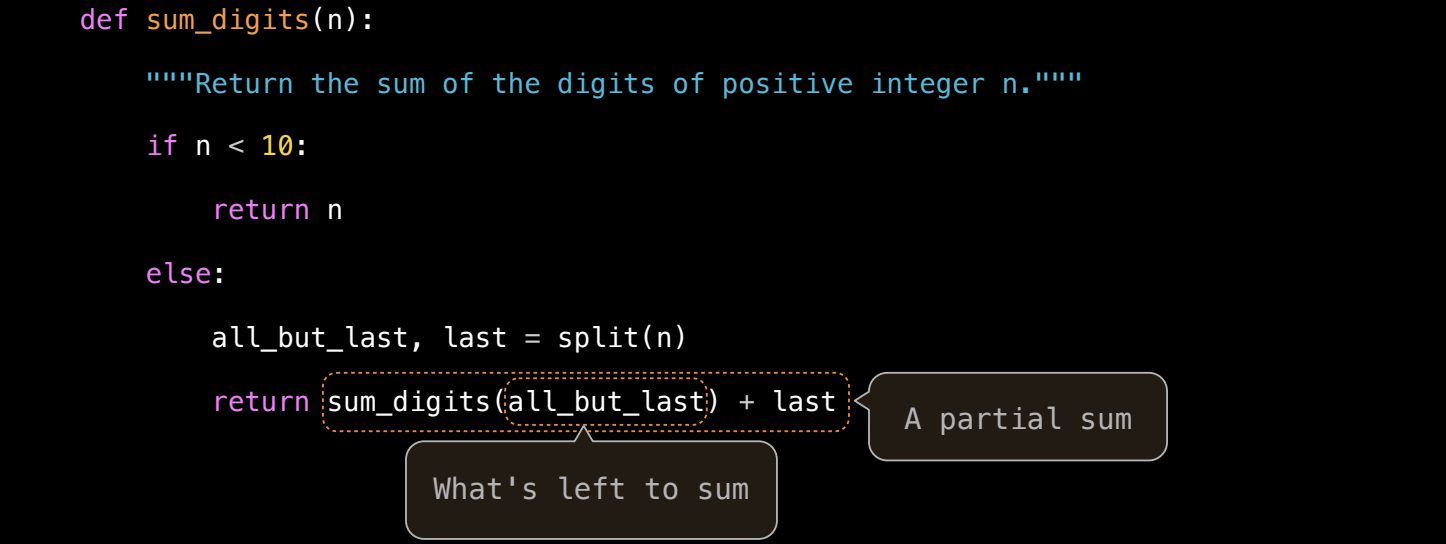
image-20240911113720436

def sum_digits(n):
    if n < 10:
        return n
    else:
        all_but_last, last = split(n)
        return sum_digits(all_but_last) + last
迭代版数字求和 
def sum_digits_iter(n):
    digit_sum = 0
    while n > 0:
        n, last = split(n)
        digit_sum += last
    return digit_sum

通过 while 循环不断提取最后一位数字并累加到 digit_sum，直到所有位数都处理完毕。

迭代到递归的转化

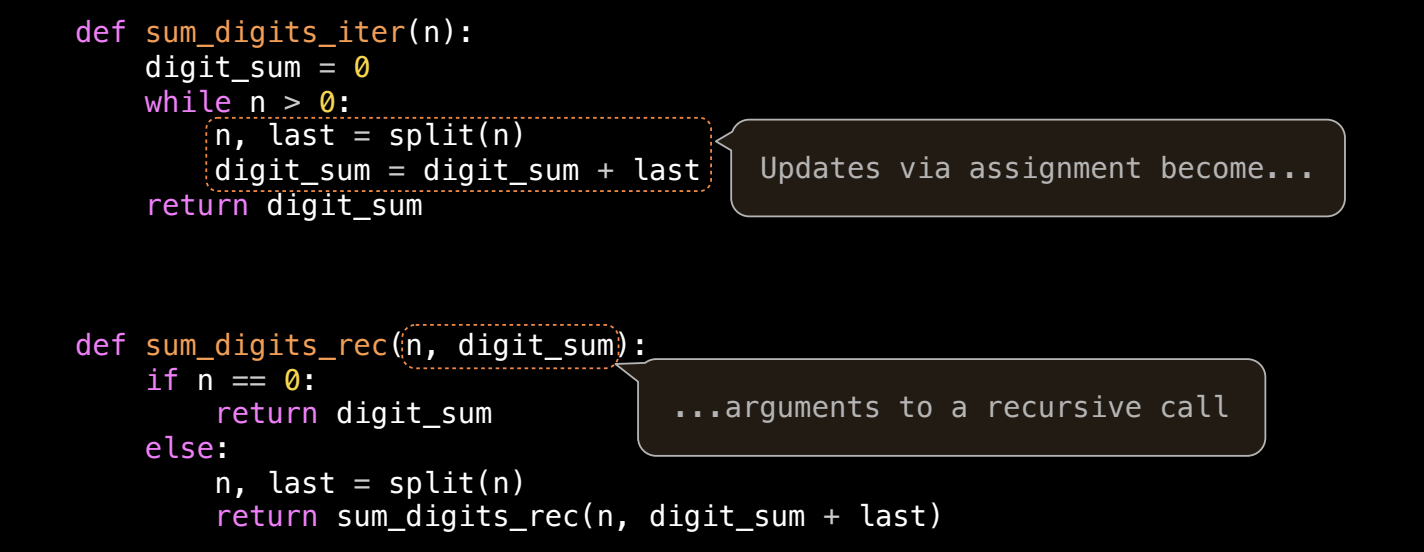
image-20240911113739916

8将迭代转化为递归相对直接：在递归中通过传递状态来替代迭代中的变量更新。比如，将 while 循环的状态传递给递归调用。

递归转化后的数字求和

def sum_digits_recursive(n, digit_sum=0):
    if n == 0:
        return digit_sum
    else:
        n, last = split(n)
        return sum_digits_recursive(n, digit_sum + last)

在这个递归版本中，我们通过递归调用不断更新 n 和 digit_sum，直到 n 变为 0，然后返回累加的结果。

总结

  • 递归与迭代：递归可以简化问题的逻辑表达，特别是像阶乘或数字求和这类递归结构天然适合递归解决。而迭代则通过显式状态更新来逐步解决问题。
  • 互相递归：通过两个函数互相调用可以解决复杂的递归问题，例如 Luhn 算法。
  • 递归与迭代的转化：递归和迭代在本质上可以相互转化。通过分析递归中传递的状态变量，可以轻松将递归转化为迭代；反过来，迭代中的状态更新可以作为递归调用的参数来传递。

在递归和迭代的选择中，递归提供了更直观的代码逻辑，适合描述具有递归性质的问题；迭代在处理大规模数据时效率更高，避免了递归调用栈的开销。